11.2.2 三角形的外角 课时培优练(含解析) 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 11.2.2 三角形的外角 课时培优练(含解析) 2023-2024学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 231.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 00:00:00 | ||
图片预览


文档简介
11.2.2 三角形的外角 课时培优练 人教版八年级数学上册
一、选择题
1.如图,直线,若,,则的度数为( )
A. B. C. D.
2.如图,,,连接,若,则的度数为 ( )
A. B. C. D.
3.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,回答正确的是( )
已知:如图,.
求证:.
证明:延长BE交 ※ 于点F,
则 ⊙ +(三角形的外角等于与它不相邻两个内角之和).
又,得=____.
故( @ 相等,两直线平行).
A.※代表AB B.⊙代表∠FEC
C.▲代表∠EFC D.@ 代表同位角
4.如图所示,在中,,分别是,边上的高,并且,交于点,若,则等于( )
A. B. C. D.
5.如图,直线,若,,则的度数是( )
A. B. C. D.
6.一次数学活动课上,小聪将一副含30°角的三角板的一条直角边和45°角的三角板的一条直角边重叠,则∠1的度数为( )
A.45° B.60° C.75° D.85°
7.将一块直角三角板与一把直尺按如图所示方式放置,若,则的大小为( )
A. B. C. D.
8.如图,已知直线,,,则等于( )
A. B. C. D.
二、填空题
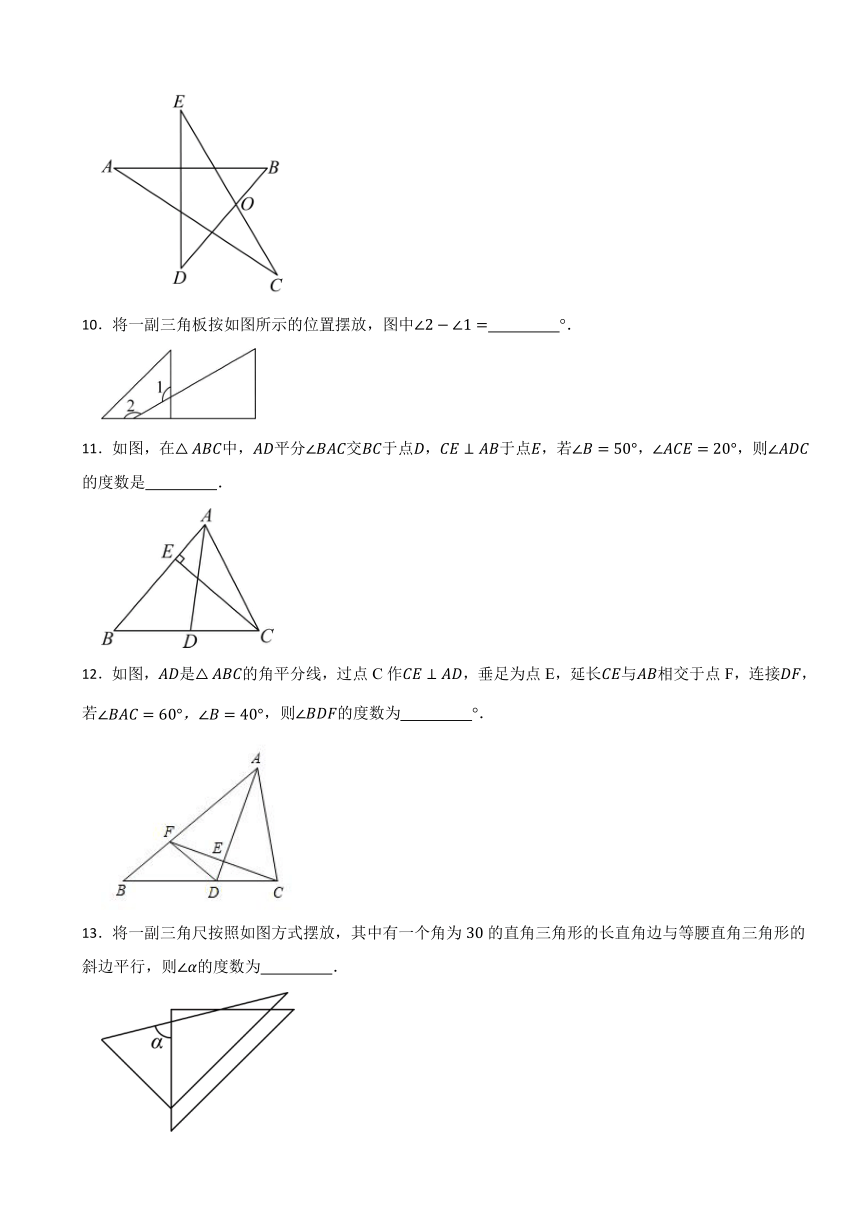
9.如图,已知,则为 .
10.将一副三角板按如图所示的位置摆放,图中 °.
11.如图,在中,平分交于点,于点,若,,则的度数是 .
12.如图,是的角平分线,过点C作,垂足为点E,延长与相交于点F,连接,若,则的度数为 °.
13.将一副三角尺按照如图方式摆放,其中有一个角为的直角三角形的长直角边与等腰直角三角形的斜边平行,则的度数为 .
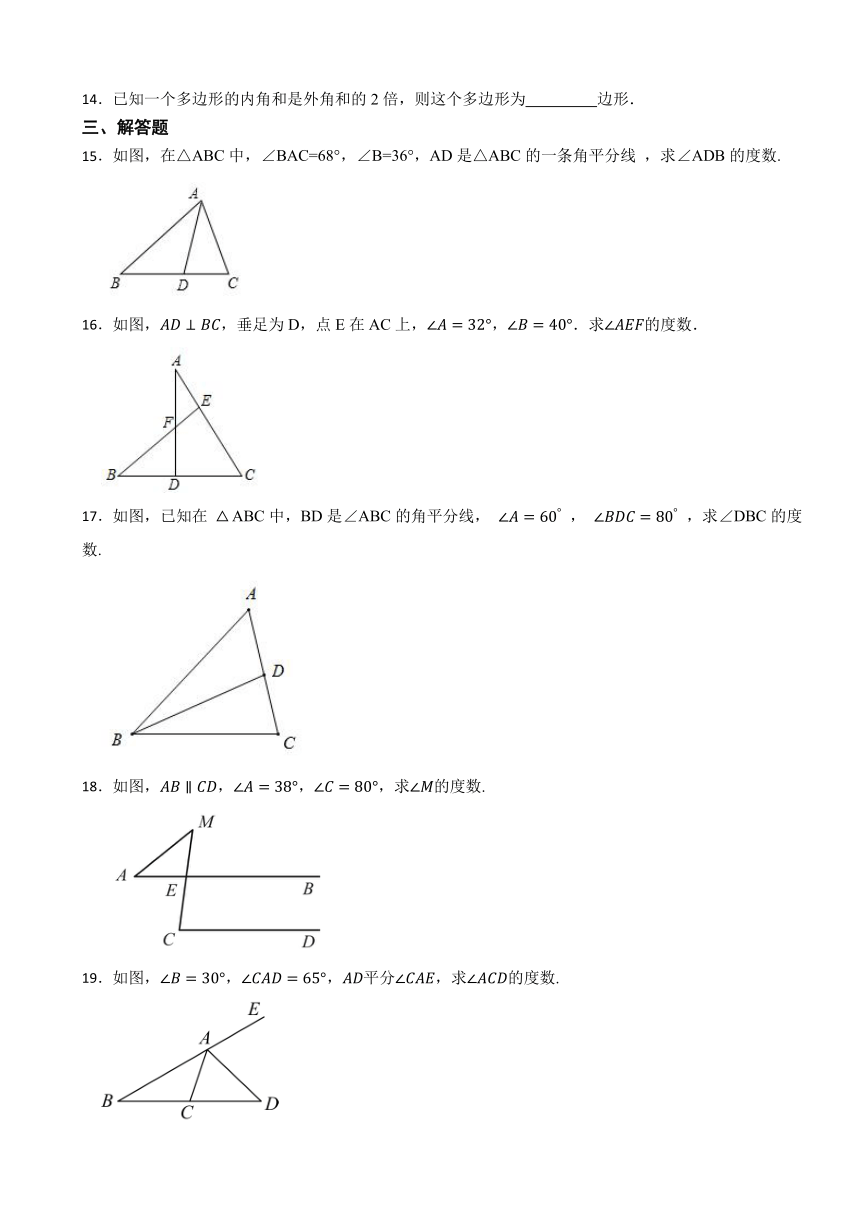
14.已知一个多边形的内角和是外角和的2倍,则这个多边形为 边形.
三、解答题
15.如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线 ,求∠ADB的度数.
16.如图,,垂足为D,点E在AC上,,.求的度数.
17.如图,已知在 ABC中,BD是∠ABC的角平分线, , ,求∠DBC的度数.
18.如图,,,,求的度数.
19.如图,,,平分,求的度数.
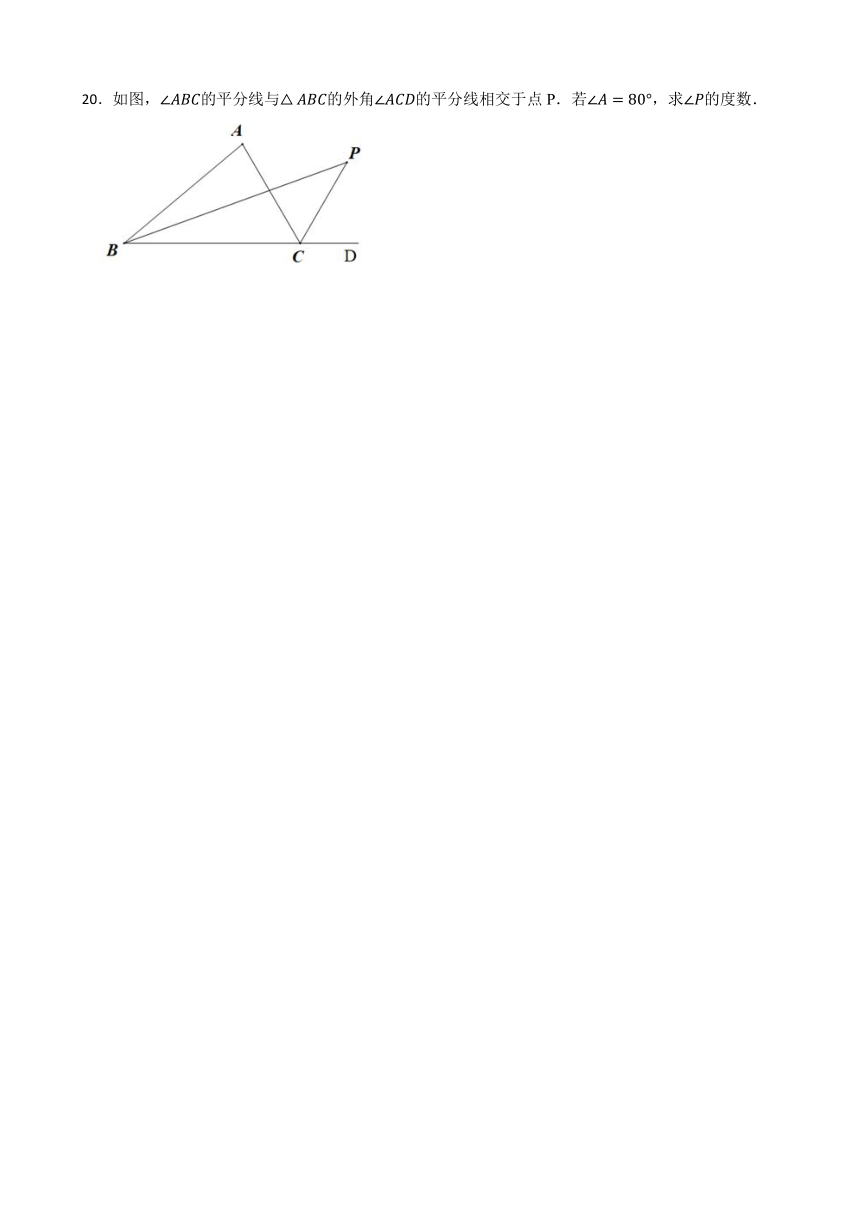
20.如图,的平分线与的外角的平分线相交于点P.若,求的度数.
答案解析部分
1.【答案】B
【解析】【解答】解:
∵a∥b,
∴∠4=∠1=70°,
∴∠4=∠2+∠5,
∴∠5=∠4-∠2=70°-46°=24°,
∴∠3=∠5=24°
故答案为B
【分析】由平行线的性质求出∠4=70°,由三角形外角的性质求出∠5=24°,由对顶角的性质得到∠3=∠5=24°
2.【答案】C
【解析】【解答】解:如图,
∵AB∥CD,
∴∠DFE=∠A=46°,
∵∠C=∠E,∠DFE=∠C+∠E,
∴∠DFE=2∠E=46°,
∴∠E=23°.
故答案为:C.
【分析】由二直线平行,同位角相等得∠DFE=∠A=46°,进而根据三角形外角性质及已知可得∠DFE=2∠E=46°,从而即可得出答案.
3.【答案】C
【解析】【解答】解: 延长BE交CD于点F,
∴∠BEC=∠EFC+∠C,
∵,
∴∠B=∠EFC,
∴AB∥CD(内错角相等,两直线平行);
即得 ※代表CD, ⊙代表∠EFC , ▲代表∠EFC , @ 代表内错角 ;
故答案为C.
【分析】延长BE交CD于点F,利用三角形外角的性质可得∠BEC=∠EFC+∠C,结合已知可得∠B=∠EFC,根据内错角相等,两直线平行即得结论.
4.【答案】A
【解析】【解答】解:∵,,
∴,
又∵,
∴,
∴.
故答案为:A.
【分析】根据高的定义及三角形的内角和定理可算出∠ABE的度数,进而根据三角形外角性质,由∠BPC=90°+∠ABE即可算出答案.
5.【答案】C
6.【答案】C
【解析】【解答】解:如图:
根据题意可得:∠4=30°,∠3=45°,
由平行线的性质可得:∠2=∠3=45°,
∴∠1=∠2+∠4=45°+30°=75°,
故答案为:C.
【分析】利用平行线的性质及三角形外角的性质求解即可.
7.【答案】B
8.【答案】B
【解析】【解答】解:对图形进行点标注,
∵l1∥l2,
∴∠CEA+∠DFB=180°.
∵∠CAB=∠C+∠CEA=135°,∠DBA=∠D+∠DFB=75°,
∴∠C+∠CEA+∠D+∠DFB=210°,
∴∠C+∠D=210°-180°=30°.
故答案为:B.
【分析】对图形进行点标注,由平行线的性质可得∠CEA+∠DFB=180°,根据外角的性质可得∠CAB=∠C+∠CEA=135°,∠DBA=∠D+∠DFB=75°,然后相加即可求出∠C+∠D的度数.
9.【答案】
【解析】【解答】解:∵是△ABF的外角,
∴,
∵是△DEO的外角
∴
故答案为:55°.
【分析】由得,所以,由三角形的外角的性质即可得出的度数。
10.【答案】30
【解析】【解答】解:∵∠1=90°+30°,∠2=90°+60°,
∴∠2-∠1=90°+60°-(90°+30°)=30°,
故答案为:30.
【分析】根据三角形外角的性质可得∠1=90°+30°,∠2=90°+60°,继而求出∠2-∠1的度数.
11.【答案】
12.【答案】40
13.【答案】
【解析】【解答】解:∵BC∥EF,∠E=45°,
∴∠DCB=∠E=45°,
∵∠B =30°,
∴ =∠B +∠DCB=30°+45°=75°;
故答案为:75°.
【分析】由平行线的性质可得∠DCB=∠E=45°,利用三角形外角的性质可得 =∠B +∠DCB,据此计算即可.
14.【答案】六
15.【答案】解:∵AD是△ABC的一条角平分线,
∴ ,
∵ ,∠BAC=68°,∠B=36°,
∴ ,
∴ .
【解析】【分析】根据角平分线的概念可得∠BAD=∠CAD=34°,由内角和定理求出∠C的度数,然后根据三角形的一个外角等于与之不相邻的两个内角的和进行求解.
16.【答案】解:∵,
∴∠ADC=90°,
∴∠C=90°-∠A=58°,
∵.
∴=∠B+∠C=58°+40°=98°.
【解析】【分析】先利用三角形的内角和求出∠C的度数,再利用三角形外角的性质可得∠AEF的度数。
17.【答案】∵∠BDC=∠A+∠ABD, , ,
∴∠ABD= ,
∵BD是∠ABC的角平分线,
∴∠DBC=∠ABD= .
【解析】【分析】根据三角形的任意一个外角等于与之不相邻的两个内角的和得出 ∠BDC=∠A+∠ABD ,从而求出∠ABD= ,再根据角平分线定义得出 ∠DBC=∠ABD ,即可求出答案.
18.【答案】解:∵,,
∴,
∵,,
∴
【解析】【分析】由平行线的性质可得∠MEB=∠C=80°,根据外角的性质可得∠MEB=∠A+∠M,据此计算.
19.【答案】解:,平分,
,
,
,
.
【解析】【分析】根据角平分线的概念可得∠EAC=2∠CAD=130°,由邻补角的性质可得∠BAC=180°-∠EAC=50°,根据外角的性质可得∠ACD=∠B+∠CAB,据此计算.
20.【答案】解:∵是的外角,
∴,
∵平分,平分,
∴,,
∵是的外角,
∴,
∴,
∴,
∴,
∵,
∴.
【解析】【分析】根据角平分线的定义可得,,再利用三角形外角的性质可得,根据等量代换可得,再求出,最后根据,可得。
一、选择题
1.如图,直线,若,,则的度数为( )
A. B. C. D.
2.如图,,,连接,若,则的度数为 ( )
A. B. C. D.
3.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,回答正确的是( )
已知:如图,.
求证:.
证明:延长BE交 ※ 于点F,
则 ⊙ +(三角形的外角等于与它不相邻两个内角之和).
又,得=____.
故( @ 相等,两直线平行).
A.※代表AB B.⊙代表∠FEC
C.▲代表∠EFC D.@ 代表同位角
4.如图所示,在中,,分别是,边上的高,并且,交于点,若,则等于( )
A. B. C. D.
5.如图,直线,若,,则的度数是( )
A. B. C. D.
6.一次数学活动课上,小聪将一副含30°角的三角板的一条直角边和45°角的三角板的一条直角边重叠,则∠1的度数为( )
A.45° B.60° C.75° D.85°
7.将一块直角三角板与一把直尺按如图所示方式放置,若,则的大小为( )
A. B. C. D.
8.如图,已知直线,,,则等于( )
A. B. C. D.
二、填空题
9.如图,已知,则为 .
10.将一副三角板按如图所示的位置摆放,图中 °.
11.如图,在中,平分交于点,于点,若,,则的度数是 .
12.如图,是的角平分线,过点C作,垂足为点E,延长与相交于点F,连接,若,则的度数为 °.
13.将一副三角尺按照如图方式摆放,其中有一个角为的直角三角形的长直角边与等腰直角三角形的斜边平行,则的度数为 .
14.已知一个多边形的内角和是外角和的2倍,则这个多边形为 边形.
三、解答题
15.如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线 ,求∠ADB的度数.
16.如图,,垂足为D,点E在AC上,,.求的度数.
17.如图,已知在 ABC中,BD是∠ABC的角平分线, , ,求∠DBC的度数.
18.如图,,,,求的度数.
19.如图,,,平分,求的度数.
20.如图,的平分线与的外角的平分线相交于点P.若,求的度数.
答案解析部分
1.【答案】B
【解析】【解答】解:
∵a∥b,
∴∠4=∠1=70°,
∴∠4=∠2+∠5,
∴∠5=∠4-∠2=70°-46°=24°,
∴∠3=∠5=24°
故答案为B
【分析】由平行线的性质求出∠4=70°,由三角形外角的性质求出∠5=24°,由对顶角的性质得到∠3=∠5=24°
2.【答案】C
【解析】【解答】解:如图,
∵AB∥CD,
∴∠DFE=∠A=46°,
∵∠C=∠E,∠DFE=∠C+∠E,
∴∠DFE=2∠E=46°,
∴∠E=23°.
故答案为:C.
【分析】由二直线平行,同位角相等得∠DFE=∠A=46°,进而根据三角形外角性质及已知可得∠DFE=2∠E=46°,从而即可得出答案.
3.【答案】C
【解析】【解答】解: 延长BE交CD于点F,
∴∠BEC=∠EFC+∠C,
∵,
∴∠B=∠EFC,
∴AB∥CD(内错角相等,两直线平行);
即得 ※代表CD, ⊙代表∠EFC , ▲代表∠EFC , @ 代表内错角 ;
故答案为C.
【分析】延长BE交CD于点F,利用三角形外角的性质可得∠BEC=∠EFC+∠C,结合已知可得∠B=∠EFC,根据内错角相等,两直线平行即得结论.
4.【答案】A
【解析】【解答】解:∵,,
∴,
又∵,
∴,
∴.
故答案为:A.
【分析】根据高的定义及三角形的内角和定理可算出∠ABE的度数,进而根据三角形外角性质,由∠BPC=90°+∠ABE即可算出答案.
5.【答案】C
6.【答案】C
【解析】【解答】解:如图:
根据题意可得:∠4=30°,∠3=45°,
由平行线的性质可得:∠2=∠3=45°,
∴∠1=∠2+∠4=45°+30°=75°,
故答案为:C.
【分析】利用平行线的性质及三角形外角的性质求解即可.
7.【答案】B
8.【答案】B
【解析】【解答】解:对图形进行点标注,
∵l1∥l2,
∴∠CEA+∠DFB=180°.
∵∠CAB=∠C+∠CEA=135°,∠DBA=∠D+∠DFB=75°,
∴∠C+∠CEA+∠D+∠DFB=210°,
∴∠C+∠D=210°-180°=30°.
故答案为:B.
【分析】对图形进行点标注,由平行线的性质可得∠CEA+∠DFB=180°,根据外角的性质可得∠CAB=∠C+∠CEA=135°,∠DBA=∠D+∠DFB=75°,然后相加即可求出∠C+∠D的度数.
9.【答案】
【解析】【解答】解:∵是△ABF的外角,
∴,
∵是△DEO的外角
∴
故答案为:55°.
【分析】由得,所以,由三角形的外角的性质即可得出的度数。
10.【答案】30
【解析】【解答】解:∵∠1=90°+30°,∠2=90°+60°,
∴∠2-∠1=90°+60°-(90°+30°)=30°,
故答案为:30.
【分析】根据三角形外角的性质可得∠1=90°+30°,∠2=90°+60°,继而求出∠2-∠1的度数.
11.【答案】
12.【答案】40
13.【答案】
【解析】【解答】解:∵BC∥EF,∠E=45°,
∴∠DCB=∠E=45°,
∵∠B =30°,
∴ =∠B +∠DCB=30°+45°=75°;
故答案为:75°.
【分析】由平行线的性质可得∠DCB=∠E=45°,利用三角形外角的性质可得 =∠B +∠DCB,据此计算即可.
14.【答案】六
15.【答案】解:∵AD是△ABC的一条角平分线,
∴ ,
∵ ,∠BAC=68°,∠B=36°,
∴ ,
∴ .
【解析】【分析】根据角平分线的概念可得∠BAD=∠CAD=34°,由内角和定理求出∠C的度数,然后根据三角形的一个外角等于与之不相邻的两个内角的和进行求解.
16.【答案】解:∵,
∴∠ADC=90°,
∴∠C=90°-∠A=58°,
∵.
∴=∠B+∠C=58°+40°=98°.
【解析】【分析】先利用三角形的内角和求出∠C的度数,再利用三角形外角的性质可得∠AEF的度数。
17.【答案】∵∠BDC=∠A+∠ABD, , ,
∴∠ABD= ,
∵BD是∠ABC的角平分线,
∴∠DBC=∠ABD= .
【解析】【分析】根据三角形的任意一个外角等于与之不相邻的两个内角的和得出 ∠BDC=∠A+∠ABD ,从而求出∠ABD= ,再根据角平分线定义得出 ∠DBC=∠ABD ,即可求出答案.
18.【答案】解:∵,,
∴,
∵,,
∴
【解析】【分析】由平行线的性质可得∠MEB=∠C=80°,根据外角的性质可得∠MEB=∠A+∠M,据此计算.
19.【答案】解:,平分,
,
,
,
.
【解析】【分析】根据角平分线的概念可得∠EAC=2∠CAD=130°,由邻补角的性质可得∠BAC=180°-∠EAC=50°,根据外角的性质可得∠ACD=∠B+∠CAB,据此计算.
20.【答案】解:∵是的外角,
∴,
∵平分,平分,
∴,,
∵是的外角,
∴,
∴,
∴,
∴,
∵,
∴.
【解析】【分析】根据角平分线的定义可得,,再利用三角形外角的性质可得,根据等量代换可得,再求出,最后根据,可得。
