第六章 一次函数单元测试卷(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
单元测试卷
(时间:120分钟 分值:150分)
一、选择题(每小题4分,共40分)
1.下列式子中,y不是x的函数的是( )
2.下列函数中,是正比例函数的是( )
3.在同一平面直角坐标系中,一次函数的图象可能是( )
4.一次函数y=(2m-1)x+2的值随x的增大而增大,则点P(-m,m)所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.端午节期间,某商场搞优惠促销活动,其活动内容是“凡在本商场一次性购买粽子超过100元者,超过100元的部分按8折优惠”.在此活动中,李明到该商场一次性购买单价为60元的礼盒x(x>2)件,则应付款 y(元)与礼盒件数x(件)之间的关系式是( )
6.如图,直线 y=2x与y=kx+b相交于y=kx+b点P(m,2),则关于x的方程kx+b=2的解是( )
B. x=1 C. x=2 D. x=4
7.将一次函数y=2x-1的图象向左平移1个单位长度,向上平移2个单位长度,得到一个新的一次函数图象,这个新的一次函数的表达式为( )
A. y=2x+2 B. y=2x+3 C. y=2x D. y=2x-1
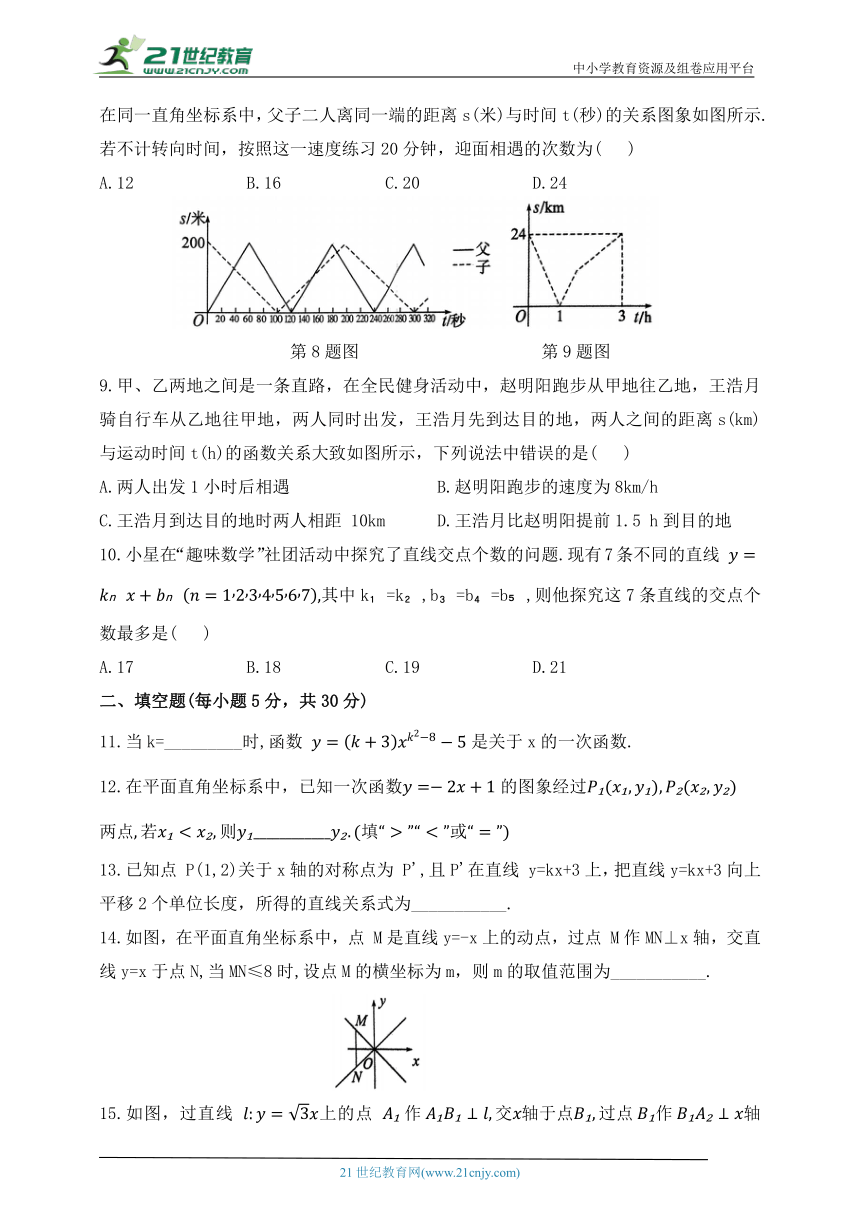
8.周末,父子二人在一段笔直的跑道上练习竞走,两人分别从跑道两端开始往返练习.在同一直角坐标系中,父子二人离同一端的距离s(米)与时间t(秒)的关系图象如图所示.若不计转向时间,按照这一速度练习20分钟,迎面相遇的次数为( )
A.12 B.16 C.20 D.24
第8题图 第9题图
9.甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,下列说法中错误的是( )
A.两人出发1小时后相遇 B.赵明阳跑步的速度为8km/h
C.王浩月到达目的地时两人相距 10km D.王浩月比赵明阳提前1.5 h到目的地
10.小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 其中k =k ,b =b =b ,则他探究这7条直线的交点个数最多是( )
A.17 B.18 C.19 D.21
二、填空题(每小题5分,共30分)
11.当k=_________时,函数 是关于x的一次函数.
12.在平面直角坐标系中,已知一次函数
13.已知点 P(1,2)关于x轴的对称点为 P',且P'在直线 y=kx+3上,把直线y=kx+3向上平移2个单位长度,所得的直线关系式为___________.
14.如图,在平面直角坐标系中,点 M是直线y=-x上的动点,过点 M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为___________.
15.如图,过直线 上的点
的长度为___________.(结果用含正整数 n的代数式表示)
第15题图 第16题图
16. A,B两地相距12千米,甲骑自行车从A 地出发前往B地,同时乙步行从B地出发前往A 地.如图的折线OPQ和线段EF分别表示甲、乙两人与A地的距离y甲、yz与时间x之间的函数关系,且OP与EF相交于点M.下列说法:
①yz与x的函数关系式是yz=-6x+12;
②点M表示甲、乙同时出发0.5小时后相遇;
③甲骑自行车的速度是18千米/小时;
④经过 或 小时,甲、乙两人相距5千米.
其中正确的序号有__________.
三、解答题(本大题共 7小题,共 80分)
17.(10分)阅读理解:已知两直线,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx-1垂直,求k的值;
(2)若一条直线经过A(2,3),且与 垂直,求这条直线的函数关系式.
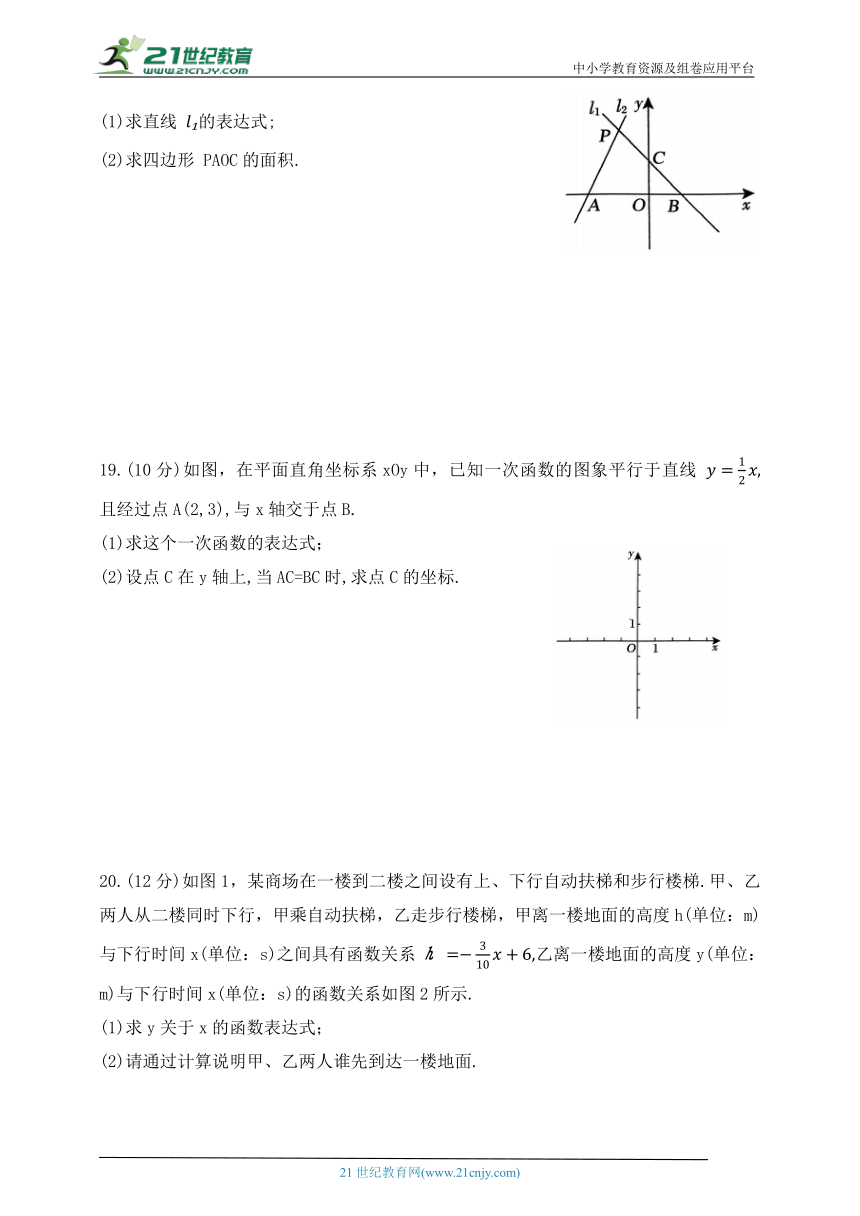
18.(10分)如图,过点 B(1,0)的直线.
(1)求直线 的表达式;
(2)求四边形 PAOC的面积.
19.(10分)如图,在平面直角坐标系xOy中,已知一次函数的图象平行于直线 且经过点A(2,3),与x轴交于点B.
(1)求这个一次函数的表达式;
(2)设点C在y轴上,当AC=BC时,求点C的坐标.
20.(12分)如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系 乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图2所示.
(1)求y关于x的函数表达式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.
21.(12分)《九章算术》中记载,浮箭漏(图1)出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间.某学校 STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
【实验观察】实验小组通过观察,每2小时记录一次箭尺读数,得到如表:
供水时间x(小时) 0 2 4 6 8
箭尺读数y(厘米) 6 18 30 42 54
【探索发现】(1)建立平面直角坐标系,如图2,横轴表示供水时间x,纵轴表示箭尺读数 y,描出以表格中数据为坐标的各点;
(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
【结论应用】应用上述发现的规律估算:
(3)供水时间达到12小时时,箭尺的读数为多少厘米
(4)如果本次实验记录的开始时间是上午8:00,那当箭尺读数为90厘米时是几点钟 (箭尺最大读数为100厘米)
22.(12分)如图,直线
(1)填空:
(2)在x轴上是否存在一点E,使△BCE的周长最短 若存在,请求出点E的坐标;若不存在,请说明理由.
23.(14分)某运输公司安排甲、乙两种货车24辆恰好一次性将328吨的物资运往A,B两地,两种货车载质量及到A,B两地的运输成本如表:
货车类型 载质量(吨/辆) 运往A 地的成本(元/辆) 运往B地的成本(元/辆)
甲种 16 1200 900
乙种 12 1000 750
(1)求甲、乙两种货车各用了多少辆;
(2)如果前往A 地的甲、乙两种货车共12辆,所运物资不少于160吨,其余货车将剩余物资运往B地.设甲、乙两种货车到A,B两地的总运输成本为w元,前往A 地的甲种货车为t辆.
①写出w与t之间的函数表达式;
②若4≤t≤10,则当t为何值时,w最小 最小值是多少
参考答案
一、选择题
1. D【解析】 当x取正数时,对于每一个x值,y有两个值与其对应,不符合函数的定义.
2. A
3. D【解析】当x=1时,两函数的值都是a +a,所以两直线的交点的横坐标为1.
若a>0,则一次函数y=ax+a 与y=a x+a的图象都从左向右上升,且都交y轴的正半轴,没有选项符合.
若a<0,则一次函数y=ax+a 是减函数,交y轴的正半轴,y=a x+a是增函数,交y轴的负半轴,且两直线的交点的横坐标为1,只有D项符合.故选 D.
4. B【解析】因为一次函数y=(2m-1)x+2的值随x的增大而增大,所以2m-1>0.解得 所以P(-m,m)在第二象限.故选 B.
5. B【解析】李明应付货款y(元)与礼盒件数x(件)的函数关系式是y=(60x-100)×0.8+100=48x+20(x>2).故选B.
6. B【解析】因为直线y=2x与y=kx+b相交于点P(m,2),所以2=2m,所以m=1.
所以点P的坐标为(1,2).所以当x=1时,y=kx+b=2,所以关于x的方程kx+b=2的解是x=1.故选 B.
7. B【解析】将一次函数y=2x-1向左平移1个单位长度,向上平移2个单位长度,则平移后的图象的函数表达式为y=2(x+1)-1+2=2x+3.故选 B.
8. B【解析】由图象知在300秒内,即5分钟内,两人相遇5次,其中迎面相遇4次.又5分钟的时间,两个分别到达相对的端点,所以20分钟内,共有4个同样的过程.所以20分钟内,迎面相遇4×4=16(次).故选 B.
9. C【解析】由图象可知,两人出发1小时后相遇,故选项A正确;赵明阳跑步的速度为24÷3=8(km/h),故选项B正确;王皓月的速度为24÷1-8=16(km/h),王皓月从开始到到达目的地用的时间为24÷16=1.5(h),故王浩月到达目的地时两人相距8×1.5=12(km),故选项C错误;王浩月比赵明阳提前3-1.5=1.5(h)到目的地,故选项D正确.故选 C.
10. B【解析】因为k =k ,b =b =b ,所以直线 中,
直线y=k x+b 与y=k x+b 无交点,y=k x+b 与y=k x+b 与y=k x+b 有1个交点,所以直线y=knx)最多有交点2×3+1=7(个),第6条线与前5条线最多有5个交点,第7条线与前6条线最多有6个交点,所以交点个数最多为7+5+6=18.故选 B.
二、填空题
11.3 【解析】因为函数 是关于x的一次函数,所以k -8=1,且k+3≠0.解得 k=3.故答案是3.
12.>
13. y=-5x+5 【解析】因为点 P(1,2)关于x轴的对称点为P',所以P'(1,-2).
因为P'在直线y=kx+3上,所以-2=k+3.解得k=-5,则y=-5x+3.
所以把直线y=kx+3向上平移2个单位长度,所得的直线关系式为y=-5x+5.
14.-4≤m≤4【解析】因为点M在直线y=-x上,所以M(m,-m).因为 MN⊥x轴,且点N在直线y=x上,所以N(m,m).所以MN=|-m-m|=|2m|.因为 MN≤8,所以|2m|≤8.所以-4≤m≤4.
【解析】直线 与x轴夹角为60°.因为OB =1,所以 所以OB =2OA =4.所以 所以所以
16.①②③【解析】①设yz与x的函数关系式是: (k≠0),因为点E(0,12),F(2,0)在函数yz=kx+b的图象上,所以 解得
即yz与x的函数关系式是 故①正确.
②由图可知,甲、乙同时出发0.5小时后,二人与A地距离相同,即二人相遇,故②正确.
③当x=0.5时,yz=-6×0.5+12=9,即两人相遇地点与A地的距离是9 km.
所以甲骑自行车的速度是9÷0.5=18(km/h),故③正确.
④设线段OP所在直线对应的y甲与x的函数关系式是y甲=ax(a≠0),
因为点(0.5,9)在函数y甲=ax的图象上,所以9=0.5a,解得a=18.
所以线段OP所在直线对应的y甲与x的函数关系式是y甲=18x.令|18x-(-6x+12)|=5.
解得 (甲 时已到达B地,不合题意,舍去),
当甲到达B地时,乙离B地5千米所走时间为5÷(12÷(时),
所以经过 时或 时时,甲、乙两人相距5km,故④不正确.
故答案为①②③.
三、解答题
17.解:(1)因为直线y=2x+1与直线 y=kx-1垂直,所以2·k=-1,解得
(2)因为过点A的直线与 垂直,所以可设过点A的直线的函数关系式为y=-3x+b,将点A(2,3)的坐标代入,得-6+b=3,解得b=9.所以过点A的直线的函数关系式为y=-3x+9.
18.解:(1)因为点 P(-1,a)在直线l :y=2x+4上,所以2×(-1)+4=a,即a=2.
则点 P的坐标为(-1,2).
设直线 的表达式为y=kx+b(k≠0),则有 解得
所以直线 的表达式为 y=-x+1.
(2)因为直线l 与y轴相交于点C,所以点C的坐标为(0,1).
又因为直线 l 与x轴相交于点A,所以点A 的坐标为(-2,0),则AB=3.
而 所以
19.解:(1)设一次函数的表达式为 y=kx+b,
因为一次函数的图象平行于直线 所以
因为一次函数的图象经过点 A(2,3),所以 解得b=2.
所以一次函数的表达式为
(2)由 令y=0,得 所以x=-4.
所以一次函数的图象与x轴的交点为B(-4,0).
因为点C在y轴上,所以设点C的坐标为(0,y).
因为AC=BC,所以 解得
经检验 是原方程的根.所以点C的坐标是
20.解:(1)设y关于x的函数表达式是y=kx+b,
由题意可得 解得
即y关于x的函数表达式是
(2)当h=0时 解得x=20;
当y=0时, 解得x=30.
因为20<30,所以甲先到达地面.
21.解:【探索发现】(1)如图.
(2)观察上述各点的分布规律,可得它们在同一条直线上.
设这条直线所对应的函数表达式为 y=kx+b(k≠0),
则 解得 所以y=6x+6.
【结论应用】应用上述发现的规律估算:
(3)当x=12时,y=6×12+6=78,所以供水时间达到12小时时,箭尺的读数为78厘米.
(4)当y=90时,6x+6=90,解得x=14,所以供水时间为 14小时.
因为本次实验记录的开始时间是上午8:00,8:00+14=22:00,
所以当箭尺读数为90厘米时是22点钟.
22.解: 4 2【解析】因为直线l :y=-x+b与x轴交于点A,且经过定点B(-1,5),所以5=1+b,所以b=4.所以直线l :y=-x+4.
因为直线l :y=-x+4 经过点C(2,m),所以m=-2+4=2,所以C(2,2).
把C(2,2)代入y=kx+1,得到2=2k+1.所以 故答案为 ;4;2.
(2)如图,作点C关于x轴的对称点C',连接BC'交x轴于点E,连接EC,则△BCE的周长最小.
因为B(-1,5),C(2,-2),所以直线BC'的表达式为
令y=0,得到 所以E的坐标为
所以存在一点 E,使△BCE的周长最短,E的坐标为
23.解:(1)设甲种货车用了x辆,则乙种货车用了(24-x)辆,
根据题意,得16x+12(24-x)=328.解得x=10.所以24-x=24-10=14.
答:甲种货车用了10辆,乙种货车用了14辆.
(2)①根据题意,得w=1 200t+1000(12-t)+900(10-t)+750[14-(12-t)]=50t+22 500.
所以w与t之间的函数表达式是w=50t+22 500.
②在 w=50t+22500中,因为 50>0,所以w随t的增大而增大.
所以当t=4 时,w取最小值,最小值是50×4+22 500=22 700.
答:当t为4时,w最小,最小值是22700.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
单元测试卷
(时间:120分钟 分值:150分)
一、选择题(每小题4分,共40分)
1.下列式子中,y不是x的函数的是( )
2.下列函数中,是正比例函数的是( )
3.在同一平面直角坐标系中,一次函数的图象可能是( )
4.一次函数y=(2m-1)x+2的值随x的增大而增大,则点P(-m,m)所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.端午节期间,某商场搞优惠促销活动,其活动内容是“凡在本商场一次性购买粽子超过100元者,超过100元的部分按8折优惠”.在此活动中,李明到该商场一次性购买单价为60元的礼盒x(x>2)件,则应付款 y(元)与礼盒件数x(件)之间的关系式是( )
6.如图,直线 y=2x与y=kx+b相交于y=kx+b点P(m,2),则关于x的方程kx+b=2的解是( )
B. x=1 C. x=2 D. x=4
7.将一次函数y=2x-1的图象向左平移1个单位长度,向上平移2个单位长度,得到一个新的一次函数图象,这个新的一次函数的表达式为( )
A. y=2x+2 B. y=2x+3 C. y=2x D. y=2x-1
8.周末,父子二人在一段笔直的跑道上练习竞走,两人分别从跑道两端开始往返练习.在同一直角坐标系中,父子二人离同一端的距离s(米)与时间t(秒)的关系图象如图所示.若不计转向时间,按照这一速度练习20分钟,迎面相遇的次数为( )
A.12 B.16 C.20 D.24
第8题图 第9题图
9.甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,下列说法中错误的是( )
A.两人出发1小时后相遇 B.赵明阳跑步的速度为8km/h
C.王浩月到达目的地时两人相距 10km D.王浩月比赵明阳提前1.5 h到目的地
10.小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 其中k =k ,b =b =b ,则他探究这7条直线的交点个数最多是( )
A.17 B.18 C.19 D.21
二、填空题(每小题5分,共30分)
11.当k=_________时,函数 是关于x的一次函数.
12.在平面直角坐标系中,已知一次函数
13.已知点 P(1,2)关于x轴的对称点为 P',且P'在直线 y=kx+3上,把直线y=kx+3向上平移2个单位长度,所得的直线关系式为___________.
14.如图,在平面直角坐标系中,点 M是直线y=-x上的动点,过点 M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为___________.
15.如图,过直线 上的点
的长度为___________.(结果用含正整数 n的代数式表示)
第15题图 第16题图
16. A,B两地相距12千米,甲骑自行车从A 地出发前往B地,同时乙步行从B地出发前往A 地.如图的折线OPQ和线段EF分别表示甲、乙两人与A地的距离y甲、yz与时间x之间的函数关系,且OP与EF相交于点M.下列说法:
①yz与x的函数关系式是yz=-6x+12;
②点M表示甲、乙同时出发0.5小时后相遇;
③甲骑自行车的速度是18千米/小时;
④经过 或 小时,甲、乙两人相距5千米.
其中正确的序号有__________.
三、解答题(本大题共 7小题,共 80分)
17.(10分)阅读理解:已知两直线,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx-1垂直,求k的值;
(2)若一条直线经过A(2,3),且与 垂直,求这条直线的函数关系式.
18.(10分)如图,过点 B(1,0)的直线.
(1)求直线 的表达式;
(2)求四边形 PAOC的面积.
19.(10分)如图,在平面直角坐标系xOy中,已知一次函数的图象平行于直线 且经过点A(2,3),与x轴交于点B.
(1)求这个一次函数的表达式;
(2)设点C在y轴上,当AC=BC时,求点C的坐标.
20.(12分)如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系 乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图2所示.
(1)求y关于x的函数表达式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.
21.(12分)《九章算术》中记载,浮箭漏(图1)出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间.某学校 STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
【实验观察】实验小组通过观察,每2小时记录一次箭尺读数,得到如表:
供水时间x(小时) 0 2 4 6 8
箭尺读数y(厘米) 6 18 30 42 54
【探索发现】(1)建立平面直角坐标系,如图2,横轴表示供水时间x,纵轴表示箭尺读数 y,描出以表格中数据为坐标的各点;
(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
【结论应用】应用上述发现的规律估算:
(3)供水时间达到12小时时,箭尺的读数为多少厘米
(4)如果本次实验记录的开始时间是上午8:00,那当箭尺读数为90厘米时是几点钟 (箭尺最大读数为100厘米)
22.(12分)如图,直线
(1)填空:
(2)在x轴上是否存在一点E,使△BCE的周长最短 若存在,请求出点E的坐标;若不存在,请说明理由.
23.(14分)某运输公司安排甲、乙两种货车24辆恰好一次性将328吨的物资运往A,B两地,两种货车载质量及到A,B两地的运输成本如表:
货车类型 载质量(吨/辆) 运往A 地的成本(元/辆) 运往B地的成本(元/辆)
甲种 16 1200 900
乙种 12 1000 750
(1)求甲、乙两种货车各用了多少辆;
(2)如果前往A 地的甲、乙两种货车共12辆,所运物资不少于160吨,其余货车将剩余物资运往B地.设甲、乙两种货车到A,B两地的总运输成本为w元,前往A 地的甲种货车为t辆.
①写出w与t之间的函数表达式;
②若4≤t≤10,则当t为何值时,w最小 最小值是多少
参考答案
一、选择题
1. D【解析】 当x取正数时,对于每一个x值,y有两个值与其对应,不符合函数的定义.
2. A
3. D【解析】当x=1时,两函数的值都是a +a,所以两直线的交点的横坐标为1.
若a>0,则一次函数y=ax+a 与y=a x+a的图象都从左向右上升,且都交y轴的正半轴,没有选项符合.
若a<0,则一次函数y=ax+a 是减函数,交y轴的正半轴,y=a x+a是增函数,交y轴的负半轴,且两直线的交点的横坐标为1,只有D项符合.故选 D.
4. B【解析】因为一次函数y=(2m-1)x+2的值随x的增大而增大,所以2m-1>0.解得 所以P(-m,m)在第二象限.故选 B.
5. B【解析】李明应付货款y(元)与礼盒件数x(件)的函数关系式是y=(60x-100)×0.8+100=48x+20(x>2).故选B.
6. B【解析】因为直线y=2x与y=kx+b相交于点P(m,2),所以2=2m,所以m=1.
所以点P的坐标为(1,2).所以当x=1时,y=kx+b=2,所以关于x的方程kx+b=2的解是x=1.故选 B.
7. B【解析】将一次函数y=2x-1向左平移1个单位长度,向上平移2个单位长度,则平移后的图象的函数表达式为y=2(x+1)-1+2=2x+3.故选 B.
8. B【解析】由图象知在300秒内,即5分钟内,两人相遇5次,其中迎面相遇4次.又5分钟的时间,两个分别到达相对的端点,所以20分钟内,共有4个同样的过程.所以20分钟内,迎面相遇4×4=16(次).故选 B.
9. C【解析】由图象可知,两人出发1小时后相遇,故选项A正确;赵明阳跑步的速度为24÷3=8(km/h),故选项B正确;王皓月的速度为24÷1-8=16(km/h),王皓月从开始到到达目的地用的时间为24÷16=1.5(h),故王浩月到达目的地时两人相距8×1.5=12(km),故选项C错误;王浩月比赵明阳提前3-1.5=1.5(h)到目的地,故选项D正确.故选 C.
10. B【解析】因为k =k ,b =b =b ,所以直线 中,
直线y=k x+b 与y=k x+b 无交点,y=k x+b 与y=k x+b 与y=k x+b 有1个交点,所以直线y=knx)最多有交点2×3+1=7(个),第6条线与前5条线最多有5个交点,第7条线与前6条线最多有6个交点,所以交点个数最多为7+5+6=18.故选 B.
二、填空题
11.3 【解析】因为函数 是关于x的一次函数,所以k -8=1,且k+3≠0.解得 k=3.故答案是3.
12.>
13. y=-5x+5 【解析】因为点 P(1,2)关于x轴的对称点为P',所以P'(1,-2).
因为P'在直线y=kx+3上,所以-2=k+3.解得k=-5,则y=-5x+3.
所以把直线y=kx+3向上平移2个单位长度,所得的直线关系式为y=-5x+5.
14.-4≤m≤4【解析】因为点M在直线y=-x上,所以M(m,-m).因为 MN⊥x轴,且点N在直线y=x上,所以N(m,m).所以MN=|-m-m|=|2m|.因为 MN≤8,所以|2m|≤8.所以-4≤m≤4.
【解析】直线 与x轴夹角为60°.因为OB =1,所以 所以OB =2OA =4.所以 所以所以
16.①②③【解析】①设yz与x的函数关系式是: (k≠0),因为点E(0,12),F(2,0)在函数yz=kx+b的图象上,所以 解得
即yz与x的函数关系式是 故①正确.
②由图可知,甲、乙同时出发0.5小时后,二人与A地距离相同,即二人相遇,故②正确.
③当x=0.5时,yz=-6×0.5+12=9,即两人相遇地点与A地的距离是9 km.
所以甲骑自行车的速度是9÷0.5=18(km/h),故③正确.
④设线段OP所在直线对应的y甲与x的函数关系式是y甲=ax(a≠0),
因为点(0.5,9)在函数y甲=ax的图象上,所以9=0.5a,解得a=18.
所以线段OP所在直线对应的y甲与x的函数关系式是y甲=18x.令|18x-(-6x+12)|=5.
解得 (甲 时已到达B地,不合题意,舍去),
当甲到达B地时,乙离B地5千米所走时间为5÷(12÷(时),
所以经过 时或 时时,甲、乙两人相距5km,故④不正确.
故答案为①②③.
三、解答题
17.解:(1)因为直线y=2x+1与直线 y=kx-1垂直,所以2·k=-1,解得
(2)因为过点A的直线与 垂直,所以可设过点A的直线的函数关系式为y=-3x+b,将点A(2,3)的坐标代入,得-6+b=3,解得b=9.所以过点A的直线的函数关系式为y=-3x+9.
18.解:(1)因为点 P(-1,a)在直线l :y=2x+4上,所以2×(-1)+4=a,即a=2.
则点 P的坐标为(-1,2).
设直线 的表达式为y=kx+b(k≠0),则有 解得
所以直线 的表达式为 y=-x+1.
(2)因为直线l 与y轴相交于点C,所以点C的坐标为(0,1).
又因为直线 l 与x轴相交于点A,所以点A 的坐标为(-2,0),则AB=3.
而 所以
19.解:(1)设一次函数的表达式为 y=kx+b,
因为一次函数的图象平行于直线 所以
因为一次函数的图象经过点 A(2,3),所以 解得b=2.
所以一次函数的表达式为
(2)由 令y=0,得 所以x=-4.
所以一次函数的图象与x轴的交点为B(-4,0).
因为点C在y轴上,所以设点C的坐标为(0,y).
因为AC=BC,所以 解得
经检验 是原方程的根.所以点C的坐标是
20.解:(1)设y关于x的函数表达式是y=kx+b,
由题意可得 解得
即y关于x的函数表达式是
(2)当h=0时 解得x=20;
当y=0时, 解得x=30.
因为20<30,所以甲先到达地面.
21.解:【探索发现】(1)如图.
(2)观察上述各点的分布规律,可得它们在同一条直线上.
设这条直线所对应的函数表达式为 y=kx+b(k≠0),
则 解得 所以y=6x+6.
【结论应用】应用上述发现的规律估算:
(3)当x=12时,y=6×12+6=78,所以供水时间达到12小时时,箭尺的读数为78厘米.
(4)当y=90时,6x+6=90,解得x=14,所以供水时间为 14小时.
因为本次实验记录的开始时间是上午8:00,8:00+14=22:00,
所以当箭尺读数为90厘米时是22点钟.
22.解: 4 2【解析】因为直线l :y=-x+b与x轴交于点A,且经过定点B(-1,5),所以5=1+b,所以b=4.所以直线l :y=-x+4.
因为直线l :y=-x+4 经过点C(2,m),所以m=-2+4=2,所以C(2,2).
把C(2,2)代入y=kx+1,得到2=2k+1.所以 故答案为 ;4;2.
(2)如图,作点C关于x轴的对称点C',连接BC'交x轴于点E,连接EC,则△BCE的周长最小.
因为B(-1,5),C(2,-2),所以直线BC'的表达式为
令y=0,得到 所以E的坐标为
所以存在一点 E,使△BCE的周长最短,E的坐标为
23.解:(1)设甲种货车用了x辆,则乙种货车用了(24-x)辆,
根据题意,得16x+12(24-x)=328.解得x=10.所以24-x=24-10=14.
答:甲种货车用了10辆,乙种货车用了14辆.
(2)①根据题意,得w=1 200t+1000(12-t)+900(10-t)+750[14-(12-t)]=50t+22 500.
所以w与t之间的函数表达式是w=50t+22 500.
②在 w=50t+22500中,因为 50>0,所以w随t的增大而增大.
所以当t=4 时,w取最小值,最小值是50×4+22 500=22 700.
答:当t为4时,w最小,最小值是22700.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
