1.3 探索三角形全等的条件 同步精练(含答案)苏科版数学八年级上册
文档属性
| 名称 | 1.3 探索三角形全等的条件 同步精练(含答案)苏科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 176.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 00:00:00 | ||
图片预览



文档简介
1.3 探索三角形全等的条件
一、单选题
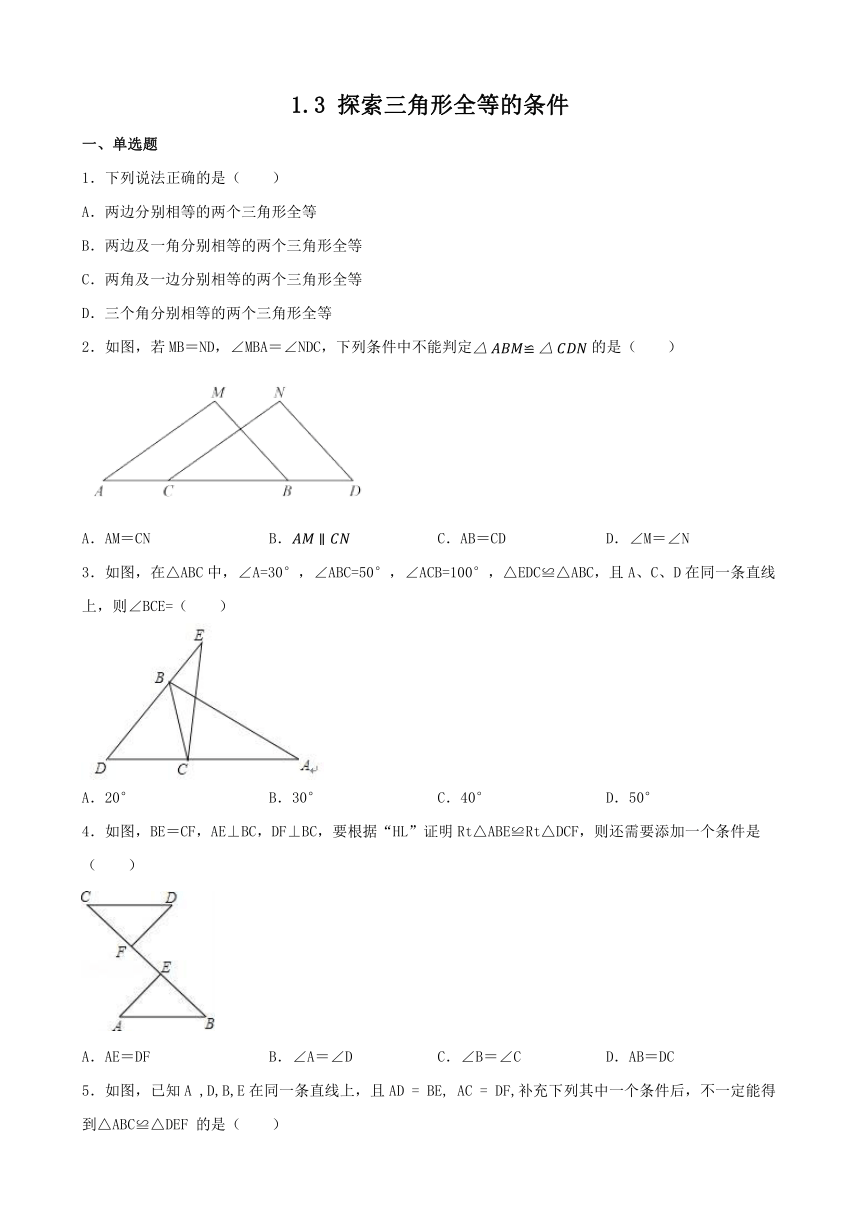
1.下列说法正确的是( )
A.两边分别相等的两个三角形全等
B.两边及一角分别相等的两个三角形全等
C.两角及一边分别相等的两个三角形全等
D.三个角分别相等的两个三角形全等
2.如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定的是( )
A.AM=CN B. C.AB=CD D.∠M=∠N
3.如图,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且A、C、D在同一条直线上,则∠BCE=( )
A.20° B.30° C.40° D.50°
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC
5.如图,已知A ,D,B,E在同一条直线上,且AD = BE, AC = DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF 的是( )
A.BC = EF B.AC//DF
C.∠C = ∠F D.∠BAC = ∠EDF
6.如图,用三角尺可按下面的方法画角平分线:在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,通过证明△OMP≌△ONP可以说明OP是∠AOB的角平分线,那么△OMP≌△ONP的依据是( )
A.SSS B.SAS C.AAS D.HL
7.如图,在 ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC交AD于E,过E作EF∥AC交BC于F,那么下列结论一定成立的是( )
A.∠ABE=∠C B.AE=BE C.AB=BF D.BE=EF
8.如图,在①AB=AC②AD=AE③∠B=∠C④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( )
A.①②③ B.②③④ C.①②④ D.③②④
二、填空题
9.如图:已知AB⊥BC,AE⊥DE,且AB=AE,∠ACD=∠ADC=50°,∠BAD=100°,则∠BAE= .
10.如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为 cm.
11.如图,ABC的面积为6cm2,AP垂直∠ABC的平分线BP于点P,则PBC的面积是 cm2.
12.如图所示:已知点F、E分别在AB、AC上,且AE=AF,请你补充一个条件: ,使得△ABE≌△ACF.(只需填写一种情况即可)
13.如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当AP= 时,以点A,P,Q为顶点的三角形与△ABC全等.
三、解答题
14.如图,在 中, ,点D,E分别为 上的点, ,若 ,求证: .
15.看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF
16.如图,,,,,垂足分别是D,E,BE=0.8,DE=1.7,求AD的长.
17.如图,在△ABC中,AD是BC边上的中线,F,E分别是AD及其延长线上的点.
(1)如果CFBE,说明:△BDE≌△CDF;
(2)若CF,BE是△ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E、F,请猜想BF与CE的位置关系?并说明理由.
参考答案
1.C
2.A
3.A
4.D
5.C
6.D
7.C
8.C
9.120°
10.12
11.3
12.AB=AC(答案不唯一)
13.10或20
14.证明: , ,
.
,
.
在 和 中,
,
.
15.证明: ∵BC∥EF
∴∠ABC=∠E (两直线平行,同位角相等)
∵AD=BE
∴ AD+DB=BE+DB;即:AB=DE
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS) .
16.解:∵,,
∴,
∴,
∵,,
∴,
∴,
∵,
∴
在和中
∴,
∴,
17.(1)证明:∵CFBE,∴∠FCD﹦∠EBD.∵AD是BC边上的中线,∴.在△BDE和△CDF中,,∴△BDE≌△CDF.
(2)解:BFCE.理由如下:如图,连接BF,CE.
∵ CF⊥AD于F,BE⊥AD于E,∴CFBE.由(1)的结论可知△BDE≌△CDF,∴.∵AD是BC边上的中线,∴BD =CD.在△BDF和△CDE中,,∴△BDF≌△CDE.∴,∴BFCE
一、单选题
1.下列说法正确的是( )
A.两边分别相等的两个三角形全等
B.两边及一角分别相等的两个三角形全等
C.两角及一边分别相等的两个三角形全等
D.三个角分别相等的两个三角形全等
2.如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定的是( )
A.AM=CN B. C.AB=CD D.∠M=∠N
3.如图,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且A、C、D在同一条直线上,则∠BCE=( )
A.20° B.30° C.40° D.50°
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC
5.如图,已知A ,D,B,E在同一条直线上,且AD = BE, AC = DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF 的是( )
A.BC = EF B.AC//DF
C.∠C = ∠F D.∠BAC = ∠EDF
6.如图,用三角尺可按下面的方法画角平分线:在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,通过证明△OMP≌△ONP可以说明OP是∠AOB的角平分线,那么△OMP≌△ONP的依据是( )
A.SSS B.SAS C.AAS D.HL
7.如图,在 ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC交AD于E,过E作EF∥AC交BC于F,那么下列结论一定成立的是( )
A.∠ABE=∠C B.AE=BE C.AB=BF D.BE=EF
8.如图,在①AB=AC②AD=AE③∠B=∠C④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( )
A.①②③ B.②③④ C.①②④ D.③②④
二、填空题
9.如图:已知AB⊥BC,AE⊥DE,且AB=AE,∠ACD=∠ADC=50°,∠BAD=100°,则∠BAE= .
10.如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为 cm.
11.如图,ABC的面积为6cm2,AP垂直∠ABC的平分线BP于点P,则PBC的面积是 cm2.
12.如图所示:已知点F、E分别在AB、AC上,且AE=AF,请你补充一个条件: ,使得△ABE≌△ACF.(只需填写一种情况即可)
13.如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当AP= 时,以点A,P,Q为顶点的三角形与△ABC全等.
三、解答题
14.如图,在 中, ,点D,E分别为 上的点, ,若 ,求证: .
15.看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF
16.如图,,,,,垂足分别是D,E,BE=0.8,DE=1.7,求AD的长.
17.如图,在△ABC中,AD是BC边上的中线,F,E分别是AD及其延长线上的点.
(1)如果CFBE,说明:△BDE≌△CDF;
(2)若CF,BE是△ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E、F,请猜想BF与CE的位置关系?并说明理由.
参考答案
1.C
2.A
3.A
4.D
5.C
6.D
7.C
8.C
9.120°
10.12
11.3
12.AB=AC(答案不唯一)
13.10或20
14.证明: , ,
.
,
.
在 和 中,
,
.
15.证明: ∵BC∥EF
∴∠ABC=∠E (两直线平行,同位角相等)
∵AD=BE
∴ AD+DB=BE+DB;即:AB=DE
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS) .
16.解:∵,,
∴,
∴,
∵,,
∴,
∴,
∵,
∴
在和中
∴,
∴,
17.(1)证明:∵CFBE,∴∠FCD﹦∠EBD.∵AD是BC边上的中线,∴.在△BDE和△CDF中,,∴△BDE≌△CDF.
(2)解:BFCE.理由如下:如图,连接BF,CE.
∵ CF⊥AD于F,BE⊥AD于E,∴CFBE.由(1)的结论可知△BDE≌△CDF,∴.∵AD是BC边上的中线,∴BD =CD.在△BDF和△CDE中,,∴△BDF≌△CDE.∴,∴BFCE
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
