沪科版八年级上册 第12章 一次函数 单元综合水平检测试题(含答案)
文档属性
| 名称 | 沪科版八年级上册 第12章 一次函数 单元综合水平检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 128.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 22:02:19 | ||
图片预览



文档简介
2023-2024学年沪科版八年级上册
第12章一次函数单元综合水平检测试题
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在函数中,自变量的取值范围是( )
A. B. C. 且 D. 且
2. 下列图象中,表示是的函数的是( )
A. B. C. D.
3. 一支签字笔的单价为元,小涵同学拿了元钱去购买了支该型号的签字笔,写出所剩余的钱与间的关系式是( )
A. B. C. D.
4. 某周末,亮亮全家上午时自驾小汽车从家里出发,到某网红地游玩,该小汽车离家的距离千米与时间时之间的关系如图所示,根据图象提供的有关信息,判断下列说法错误的是( )
A. 景点离亮亮的家千米 B. 时至时,小汽车匀速行驶
C. 小汽车返程的速度为千米时 D. 亮亮到家的时间为时
5. 若正比例函数的图象经过不同象限的两点和,则一次函数的图象所经过的象限是( )
A. 一、二、三象限 B. 二、三、四象限 C. 一、二、四象限 D. 一、三、四象限
6. 有下列函数:;;;;其中是一次函数的有( )
A. 个 B. 个 C. 个 D. 个
7. 在同一平面直角坐标系中,一次函数的与的图象可能是( )
A. B. C. D.
8. 若函数的图象上有两点,则下列说法正确的是( )
A. B. C. D. 无法确定
9. 如图,一直线与两坐标轴的正半轴分别交,两点,是线段上任意一点不包括端点,过点分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为,则该直线的函数表达式是( )
A. B.
C. D.
10. 如图,函数和的图象交于点,则根据图象可得,关于、的二元一次方程组的解是( )
A. B.
C. D.
11. A、两地相距,甲骑自行车从地出发前往地,同时乙步行从地出发前往地,如图所示的折线和线段分别表示甲、乙两人与地的距离与时间之间的函数关系,且与交于点下列说法中错误的是( )
A. 甲乙出发后相遇 B. 甲骑自行车的速度为
C. 两人相遇地点与地的距离为 D. 甲、乙相距时,出发时间为
12. 已知关于,的方程组的解是,则直线与直线的交点坐标是( )
A. B. C. D.
二、填空题(本大题共8小题,共24.0分)
13. 一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加,小球速度与时间之间的关系为 .
14. 如图所示是关于变量,的程序计算,若开始输入的值为,则最后输出因变量的值为 .
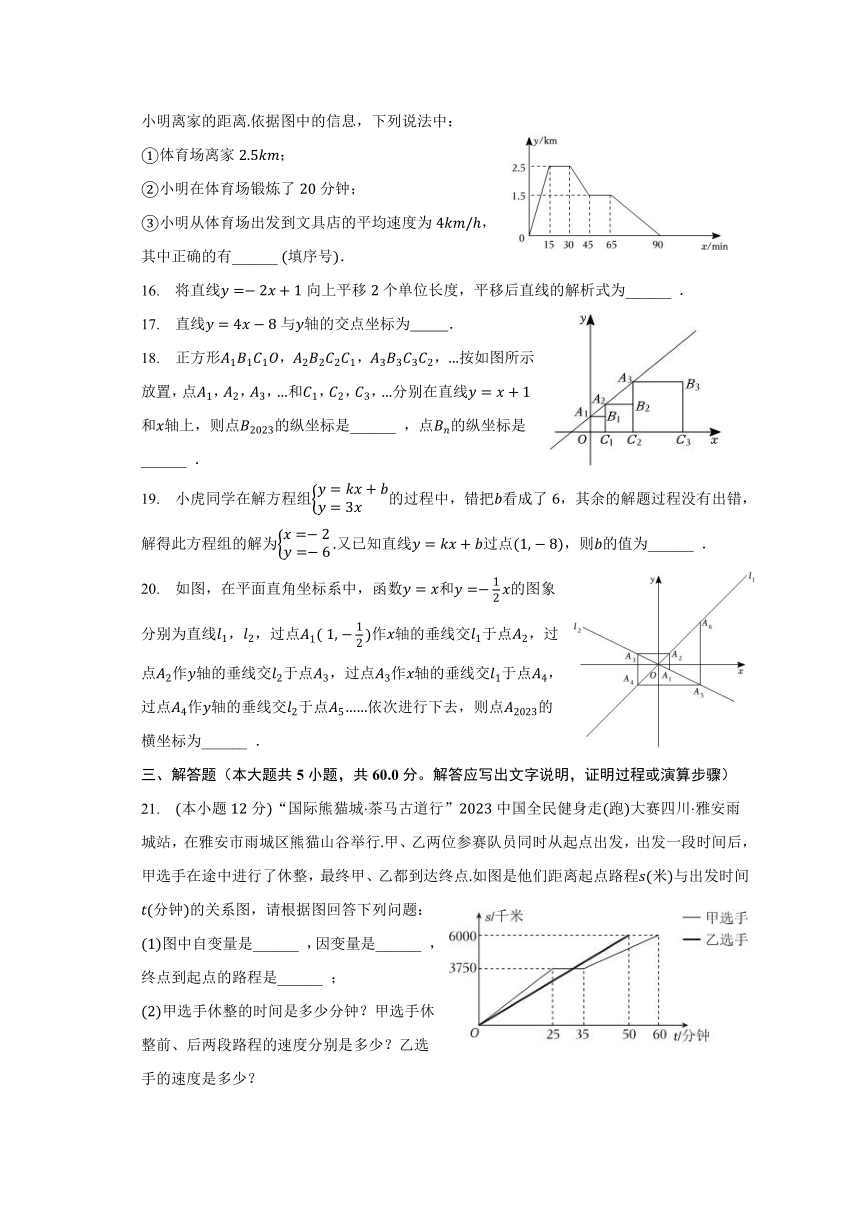
15. 已知小明家、体育场、文具店在同一直线上,图中的信息反映的过程是:小明从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家图中表示时间,表示小明离家的距离依据图中的信息,下列说法中:
体育场离家;
小明在体育场锻炼了分钟;
小明从体育场出发到文具店的平均速度为,
其中正确的有______ 填序号.
16. 将直线向上平移个单位长度,平移后直线的解析式为______ .
17. 直线与轴的交点坐标为 .
18. 正方形,,,按如图所示放置,点,,,和,,,分别在直线和轴上,则点的纵坐标是______ ,点的纵坐标是______ .
19. 小虎同学在解方程组的过程中,错把看成了,其余的解题过程没有出错,解得此方程组的解为又已知直线过点,则的值为______ .
20. 如图,在平面直角坐标系中,函数和的图象分别为直线,,过点作轴的垂线交于点,过点作轴的垂线交于点,过点作轴的垂线交于点,过点作轴的垂线交于点依次进行下去,则点的横坐标为______ .
三、解答题(本大题共5小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
21. 本小题分“国际熊猫城茶马古道行”中国全民健身走跑大赛四川雅安雨城站,在雅安市雨城区熊猫山谷举行甲、乙两位参赛队员同时从起点出发,出发一段时间后,甲选手在途中进行了休整,最终甲、乙都到达终点如图是他们距离起点路程米与出发时间分钟的关系图,请根据图回答下列问题:
图中自变量是______ ,因变量是______ ,终点到起点的路程是______ ;
甲选手休整的时间是多少分钟?甲选手休整前、后两段路程的速度分别是多少?乙选手的速度是多少?
比赛开始后,甲乙两人第一次相遇时的时间是多少分钟?
22. 本小题分已知一次函数,当时,.
求一次函数解析式,并在下面的平面直角坐标系中画出该函数图象;
若该直线与轴交于点,与轴交于点,求的面积;
把该直线沿着轴向上平移______ 个单位经过原点.
23. 本小题分 如图,直线的函数表达式为,且直线与轴交于点,直线:与轴交于点,且经过点,直线与交于点.
求点和点的坐标;
求直线的函数表达式;
利用函数图象写出关于,的二元一次方程组的解.
24. 本小题分如图,直线:与坐标轴的交点分别为,,直线与坐标轴交于,两点.
求直线与直线的交点的坐标.
直接写出不等式的解集.
求四边形的面积.
25. 本小题分学校通过劳动教育促进学生树德、增智、强体、育美全面发展,计划组织八年级学生到“开心”农场开展劳动实践活动到达农场后分组进行劳动,若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生劳动实践结束后,学校在租车总费用元的限额内,租用汽车送师生返校,每辆车上至少要有名老师现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 乙型客车
载客量人辆
租金元辆
参加本次实践活动的老师和学生各有多少名?
租车返校时,既要保证所有师生都有车坐,又要保证每辆车上至少有名老师,则共需租车______ 辆;
学校共有几种租车方案?最少租车费用是多少?
第12章一次函数单元综合水平检测试题答案
2. 3. 4. 5. 6.
7. 8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18.
19.
20.
21. 解:由图可得图中自变量是出发时间,因变量是距离起点路程,终点到起点的路程是米,
故答案为:出发时间;距离起点路程;米;
由图可得,甲选手休整的时间为,
甲选手休整前路程为米,用了分钟,
甲选手休整前的速度为,
甲选手休整后的速度为,
乙选手的平均速度为;
答:甲选手休整的时间是分钟,甲选手休整前、后两段路程的速度分别是、,乙选手的速度是;
由图可得,甲乙两个选手在距离起点米的位置相遇,由可知乙选手的平均速度为,
甲乙第一次相遇的时间为.
答:甲乙两人第一次相遇时的时间是分钟.
22. 解:当时,,
,
,
,
当时,;当时,,
图象如右侧:
由可知,,
,,
;
把向上平移个单位后经过原点.
23. 解:在中
令,即 解得,
,
点在直线上,
,
,
;
设直线的函数表达式为,
由题意得:,
解得:,
;
由图可知,二元一次方程组的解为.
24. 解:把、的坐标代入得:,
解得:,,
所以直线的解析式是,
解方程组得:,
所以点的坐标是;
由图象可知,时,的图象在的图象的上方,
故不等式的解集是;
,
当时,,
当时,,
则点的坐标是,点的坐标是,
点坐标是,点坐标是,
所以四边形的面积
.
25. 解:设老师有名,学生有名,根据题意,列方程组为:
,解得,
答:老师有名,学生有名.
每辆车上至少有名老师,
汽车总数不能大于辆,
要保证名师生有车坐,汽车总数不能少于取整数辆,
综合可知汽车总数为辆.
故答案为:.
设租用甲客车辆,则租车费用元是的函数,即:
,
整理得:,
学校在租车总费用元的限额内,租用汽车送师生返校,
,
,即.
要保证人有车坐,不能小于,所以有两种租车方案:
方案一:租辆甲种客车,辆乙种客车;
方案二:租辆甲种客车,辆乙种客车;
随的增大而增大,
当时,最小,.
答:学校共有两套租车方案,最少费用为元,
第12章一次函数单元综合水平检测试题
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在函数中,自变量的取值范围是( )
A. B. C. 且 D. 且
2. 下列图象中,表示是的函数的是( )
A. B. C. D.
3. 一支签字笔的单价为元,小涵同学拿了元钱去购买了支该型号的签字笔,写出所剩余的钱与间的关系式是( )
A. B. C. D.
4. 某周末,亮亮全家上午时自驾小汽车从家里出发,到某网红地游玩,该小汽车离家的距离千米与时间时之间的关系如图所示,根据图象提供的有关信息,判断下列说法错误的是( )
A. 景点离亮亮的家千米 B. 时至时,小汽车匀速行驶
C. 小汽车返程的速度为千米时 D. 亮亮到家的时间为时
5. 若正比例函数的图象经过不同象限的两点和,则一次函数的图象所经过的象限是( )
A. 一、二、三象限 B. 二、三、四象限 C. 一、二、四象限 D. 一、三、四象限
6. 有下列函数:;;;;其中是一次函数的有( )
A. 个 B. 个 C. 个 D. 个
7. 在同一平面直角坐标系中,一次函数的与的图象可能是( )
A. B. C. D.
8. 若函数的图象上有两点,则下列说法正确的是( )
A. B. C. D. 无法确定
9. 如图,一直线与两坐标轴的正半轴分别交,两点,是线段上任意一点不包括端点,过点分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为,则该直线的函数表达式是( )
A. B.
C. D.
10. 如图,函数和的图象交于点,则根据图象可得,关于、的二元一次方程组的解是( )
A. B.
C. D.
11. A、两地相距,甲骑自行车从地出发前往地,同时乙步行从地出发前往地,如图所示的折线和线段分别表示甲、乙两人与地的距离与时间之间的函数关系,且与交于点下列说法中错误的是( )
A. 甲乙出发后相遇 B. 甲骑自行车的速度为
C. 两人相遇地点与地的距离为 D. 甲、乙相距时,出发时间为
12. 已知关于,的方程组的解是,则直线与直线的交点坐标是( )
A. B. C. D.
二、填空题(本大题共8小题,共24.0分)
13. 一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加,小球速度与时间之间的关系为 .
14. 如图所示是关于变量,的程序计算,若开始输入的值为,则最后输出因变量的值为 .
15. 已知小明家、体育场、文具店在同一直线上,图中的信息反映的过程是:小明从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家图中表示时间,表示小明离家的距离依据图中的信息,下列说法中:
体育场离家;
小明在体育场锻炼了分钟;
小明从体育场出发到文具店的平均速度为,
其中正确的有______ 填序号.
16. 将直线向上平移个单位长度,平移后直线的解析式为______ .
17. 直线与轴的交点坐标为 .
18. 正方形,,,按如图所示放置,点,,,和,,,分别在直线和轴上,则点的纵坐标是______ ,点的纵坐标是______ .
19. 小虎同学在解方程组的过程中,错把看成了,其余的解题过程没有出错,解得此方程组的解为又已知直线过点,则的值为______ .
20. 如图,在平面直角坐标系中,函数和的图象分别为直线,,过点作轴的垂线交于点,过点作轴的垂线交于点,过点作轴的垂线交于点,过点作轴的垂线交于点依次进行下去,则点的横坐标为______ .
三、解答题(本大题共5小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
21. 本小题分“国际熊猫城茶马古道行”中国全民健身走跑大赛四川雅安雨城站,在雅安市雨城区熊猫山谷举行甲、乙两位参赛队员同时从起点出发,出发一段时间后,甲选手在途中进行了休整,最终甲、乙都到达终点如图是他们距离起点路程米与出发时间分钟的关系图,请根据图回答下列问题:
图中自变量是______ ,因变量是______ ,终点到起点的路程是______ ;
甲选手休整的时间是多少分钟?甲选手休整前、后两段路程的速度分别是多少?乙选手的速度是多少?
比赛开始后,甲乙两人第一次相遇时的时间是多少分钟?
22. 本小题分已知一次函数,当时,.
求一次函数解析式,并在下面的平面直角坐标系中画出该函数图象;
若该直线与轴交于点,与轴交于点,求的面积;
把该直线沿着轴向上平移______ 个单位经过原点.
23. 本小题分 如图,直线的函数表达式为,且直线与轴交于点,直线:与轴交于点,且经过点,直线与交于点.
求点和点的坐标;
求直线的函数表达式;
利用函数图象写出关于,的二元一次方程组的解.
24. 本小题分如图,直线:与坐标轴的交点分别为,,直线与坐标轴交于,两点.
求直线与直线的交点的坐标.
直接写出不等式的解集.
求四边形的面积.
25. 本小题分学校通过劳动教育促进学生树德、增智、强体、育美全面发展,计划组织八年级学生到“开心”农场开展劳动实践活动到达农场后分组进行劳动,若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生劳动实践结束后,学校在租车总费用元的限额内,租用汽车送师生返校,每辆车上至少要有名老师现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 乙型客车
载客量人辆
租金元辆
参加本次实践活动的老师和学生各有多少名?
租车返校时,既要保证所有师生都有车坐,又要保证每辆车上至少有名老师,则共需租车______ 辆;
学校共有几种租车方案?最少租车费用是多少?
第12章一次函数单元综合水平检测试题答案
2. 3. 4. 5. 6.
7. 8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18.
19.
20.
21. 解:由图可得图中自变量是出发时间,因变量是距离起点路程,终点到起点的路程是米,
故答案为:出发时间;距离起点路程;米;
由图可得,甲选手休整的时间为,
甲选手休整前路程为米,用了分钟,
甲选手休整前的速度为,
甲选手休整后的速度为,
乙选手的平均速度为;
答:甲选手休整的时间是分钟,甲选手休整前、后两段路程的速度分别是、,乙选手的速度是;
由图可得,甲乙两个选手在距离起点米的位置相遇,由可知乙选手的平均速度为,
甲乙第一次相遇的时间为.
答:甲乙两人第一次相遇时的时间是分钟.
22. 解:当时,,
,
,
,
当时,;当时,,
图象如右侧:
由可知,,
,,
;
把向上平移个单位后经过原点.
23. 解:在中
令,即 解得,
,
点在直线上,
,
,
;
设直线的函数表达式为,
由题意得:,
解得:,
;
由图可知,二元一次方程组的解为.
24. 解:把、的坐标代入得:,
解得:,,
所以直线的解析式是,
解方程组得:,
所以点的坐标是;
由图象可知,时,的图象在的图象的上方,
故不等式的解集是;
,
当时,,
当时,,
则点的坐标是,点的坐标是,
点坐标是,点坐标是,
所以四边形的面积
.
25. 解:设老师有名,学生有名,根据题意,列方程组为:
,解得,
答:老师有名,学生有名.
每辆车上至少有名老师,
汽车总数不能大于辆,
要保证名师生有车坐,汽车总数不能少于取整数辆,
综合可知汽车总数为辆.
故答案为:.
设租用甲客车辆,则租车费用元是的函数,即:
,
整理得:,
学校在租车总费用元的限额内,租用汽车送师生返校,
,
,即.
要保证人有车坐,不能小于,所以有两种租车方案:
方案一:租辆甲种客车,辆乙种客车;
方案二:租辆甲种客车,辆乙种客车;
随的增大而增大,
当时,最小,.
答:学校共有两套租车方案,最少费用为元,
