《第11—12章》阶段性综合练习题(含答案)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 《第11—12章》阶段性综合练习题(含答案)2023-2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 195.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 20:38:55 | ||
图片预览



文档简介
2023-2024学年人教版八年级数学上册《第11—12章》阶段性综合练习题(附答案)
一.选择题(共8小题,满分32分)
1.用三根长分别为3cm,6cm,acm的小木棒首尾相接拼成一个三角形,则a可能是( )
A.1 B.2 C.3 D.4
2.若正多边形的内角和是1080°,则该正多边形的一个外角为( )
A.45° B.60° C.72° D.90°
3.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )
A.相等 B.互余 C.互补或相等 D.不相等
4.如图,已知BP是∠ABC的平分线,AP⊥BP,若,则△ABC的面积等于( )
A.24cm2 B.30cm2 C.36cm2 D.不能确定
5.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62° B.56° C.34° D.124°
6.在下列△ABC中,正确画出AC边上的高的图形是( )
A. B.
C. D.
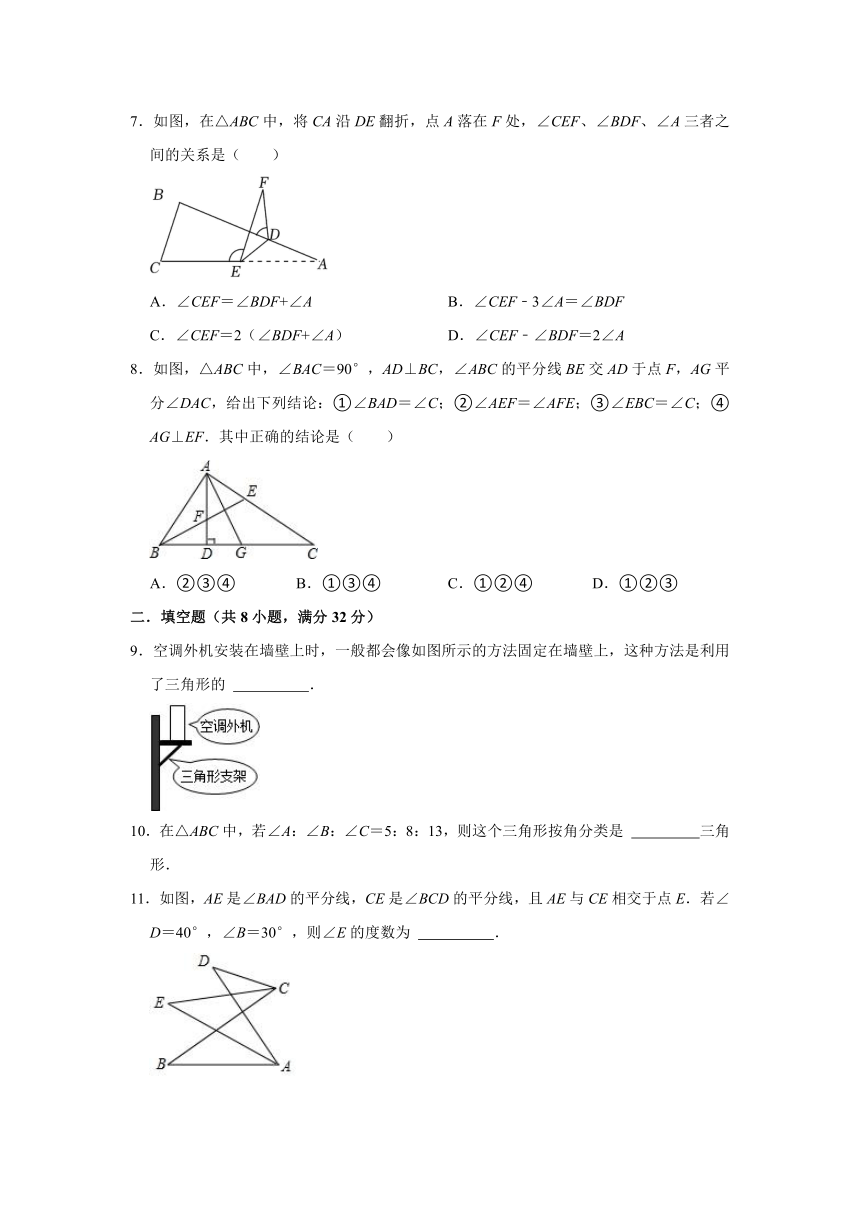
7.如图,在△ABC中,将CA沿DE翻折,点A落在F处,∠CEF、∠BDF、∠A三者之间的关系是( )
A.∠CEF=∠BDF+∠A B.∠CEF﹣3∠A=∠BDF
C.∠CEF=2(∠BDF+∠A) D.∠CEF﹣∠BDF=2∠A
8.如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.其中正确的结论是( )
A.②③④ B.①③④ C.①②④ D.①②③
二.填空题(共8小题,满分32分)
9.空调外机安装在墙壁上时,一般都会像如图所示的方法固定在墙壁上,这种方法是利用了三角形的 .
10.在△ABC中,若∠A:∠B:∠C=5:8:13,则这个三角形按角分类是 三角形.
11.如图,AE是∠BAD的平分线,CE是∠BCD的平分线,且AE与CE相交于点E.若∠D=40°,∠B=30°,则∠E的度数为 .
12.如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 °.
13.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是 .
14.如图,在△ABC中,AD为BC边的中线,E为AD上一点,连接BE并延长交AC于点F,若∠AEF=∠FAE,BE=4,EF=1.6,则CF的长为 .
15.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE= cm.
16.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= .
三.解答题(共6小题,满分56分)
17.已知三角形的三边长分别为a,b,c,化简:|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|.
18.如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.求证:BD=CE.
19.如图,在△ABC中,CD是AB边上的高,CE平分∠ACB.若∠ACB=80°,∠A比∠B大20°,求∠DCE的度数.
20.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分.
21.已知:△ABC中,BD、CE分别是AC、AB边上的高,BQ=AC,点F在CE的延长线上,CF=AB,求证:AF⊥AQ.
22.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
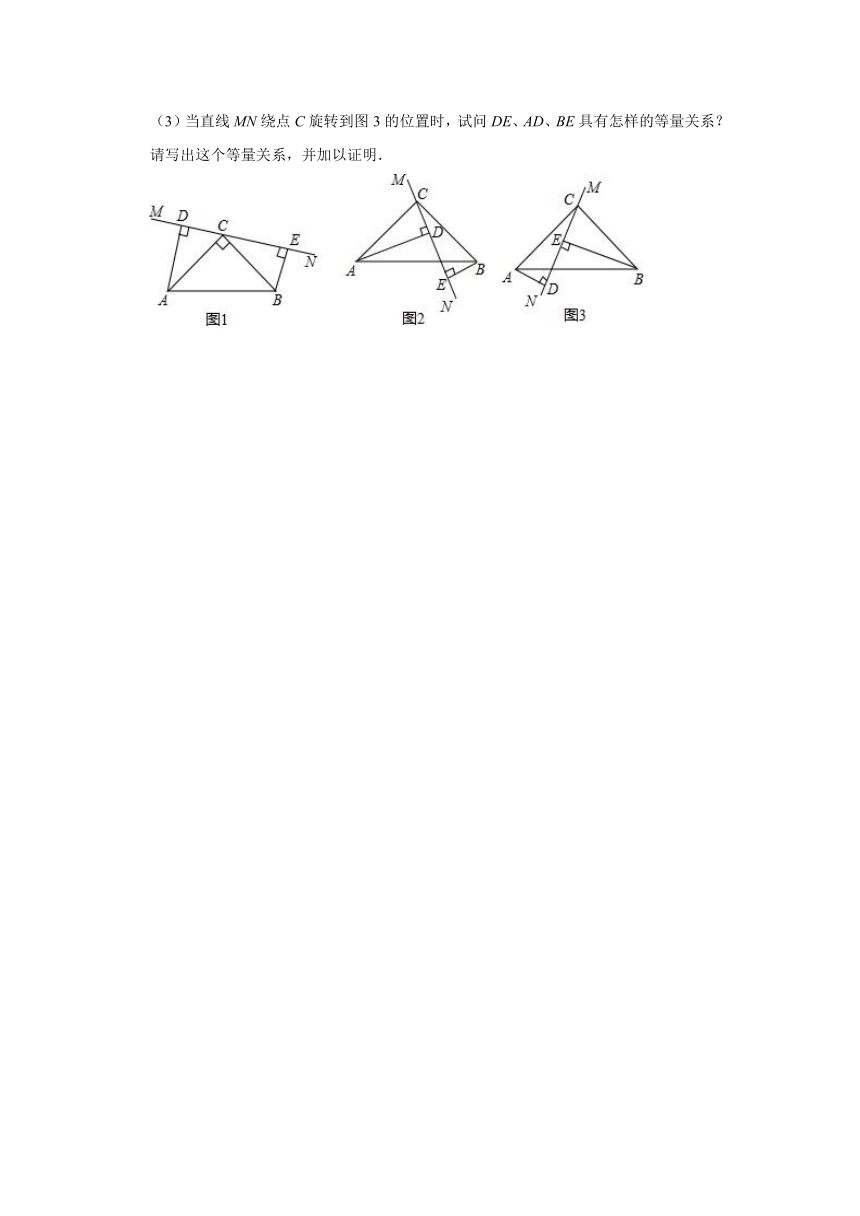
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
参考答案
一.选择题(共8小题,满分32分)
1.解:由三角形的三边关系可知:6﹣3<a<6+3,即3<a<9,
则a可能是4,
故选:D.
2.解:设这个正多边形的边数为n,
∵一个正多边形的内角和为1080°,
∴180(n﹣2)=1080,
解得:n=8,
∴这个正多边形的每一个外角是:360°÷8=45°.
故选:A.
3.解:第一种情况,当两个三角形全等时,是相等关系,
第二种情况,如图,AC=AC′,高CD=C′D′,
∴∠ADC=∠AD′C′,
在Rt△ACD和Rt△AC′D′中,
Rt△ACD≌Rt△AC′D′(HL),
∴∠CAD=∠C′AD′,
此时,∠CAB+∠C′AB=180°,
是互补关系,
所以选“相等或互补”.
故选:C.
4.解:延长AP交BC于点D,
∵BP是∠ABC的平分线,
∴∠ABP=∠DBP,
∵AP⊥BP,
∴∠APB=∠DPB=90°,
∵BP=BP,
∴△BAP≌△BDP(ASA),
∴AP=DP,
∴△APC的面积=△DPC的面积,
∵△BPC的面积=12cm2,
∴△BPD的面积+△CPD的面积=12,
∴△ABP的面积+△APC的面积=12,
∴△ABC的面积=24cm2,
故选:A.
5.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
6.解:A、AD不是AC边上的高,不符合题意;
B、AD是BC边上的高,不是AC边上的高,不符合题意;
C、BD不是AC边上的高,不符合题意;
D、BD是AC边上的高,符合题意;
故选:D.
7.解:如图,
∵∠CEF=∠A+∠AOE,∠AOE=∠F+∠BDF,
∴∠CEF=∠A+∠F+∠BDF,
由折叠性质可得:
∠A=∠F,
∴∠CEF=2∠A+∠BDF,
∴∠CEF﹣∠BDF=2∠A,
故选:D.
8.解:∵∠BAC=90°,AD⊥BC,
∴∠C+∠ABC=90°,
∠BAD+∠ABC=90°,
∴∠BAD=∠C,故①正确;
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,
∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
又∵∠AFE=∠BFD(对顶角相等),
∴∠AEF=∠AFE,故②正确;
∵∠ABE=∠CBE,
∴只有∠C=30°时∠EBC=∠C,故③错误;
∵∠AEF=∠AFE,
∴AE=AF,
∵AG平分∠DAC,
∴AG⊥EF,故④正确.
综上所述,正确的结论是①②④.
故选:C.
二.填空题(共8小题,满分32分)
9.解:这种方法应用的数学知识是:三角形的稳定性,
故答案为:稳定性.
10.解:∵∠A:∠B:∠C=5:8:13,
∴.
∴这个三角形是直角三角形.
故答案为:直角.
11.解:∵AE是∠BAD的平分线,CE是∠BCD的平分线,
∴∠DAE=∠DAB,∠DAE=∠DAB,
∵∠D+∠DCB=∠B+∠BAD①,∠D=40°,∠B=30°,
∴∠BAD﹣∠DCB=10°,
∴∠DAE﹣∠DCE=5°,
∵∠D+∠DCE=∠E+∠DAE②,
①+②,得80°+3∠DCE=30°+∠E+3∠DAE,
∴50°﹣3(∠DAE﹣∠DCE)=∠E,
∴∠E=35°,
故答案为:35°.
12.解:∵△ABC≌△ADE,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠BAD=40°,
∴∠ABD=∠ADB=(180°﹣∠BAD)=70°,
∵△ABC≌△ADE,
∴∠ADE=∠ABD=70°,
∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=114°﹣40°=74°,
∴∠E=180°﹣∠ADE﹣∠DAE=180°﹣70°﹣74°=36°,
故答案为:36.
13.解:过A点作AF⊥CD交CD的延长线于F点,如图,
∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠3,
在△ABE和△ADF中,
∵,
∴△ABE≌△ADF(AAS),
∴AE=AF=3,S△ABE=S△ADF,
∴四边形AECF是边长为3的正方形,
∴S四边形ABCD=S正方形AECF=32=9.
故答案为:9.
14.解:如图,延长AD至G,使DG=AD,连接BG,
在△BDG和△CDA中,
,
∴△BDG≌△CDA(SAS),
∴BG=AC,∠CAD=∠G,
∵∠AEF=∠FAE,
∴∠CAD=∠AEF,
∵∠BEG=∠AEF,
∴∠CAD=∠BEG,
∴∠G=∠BEG,
∴BG=BE=4,
∴AC=BE=4,
∵∠AEF=∠FAE,
∴AF=EF=1.6,
∴CF=AC﹣AF=4﹣1.6=2.4.
故答案为:2.4.
15.解:∵BE⊥CE,AD⊥CE
∴∠E=∠ADC=90°
∴∠DAC+∠DCA=90°
∵∠ACB=90°
∴∠BCE+∠DCA=90°
∴∠DAC=∠BCE
在△ACD和△CBE中,
,
∴△ACD≌△CBE
∴BE=CD=0.5(cm),EC=AD=2(cm)
DE=CE﹣CD=1.5(cm),
故答案为1.5
16.解:∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠3=∠ACB,
∵∠ACB+∠1=90°,
∴∠1+∠3=90°,
∴∠1+∠2+∠3=90°+45°=135°,
故答案为:135°.
三.解答题(共6小题,满分56分)
17.解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,则a+b﹣c>0,a﹣b﹣c<0,a+b+c>0,
∴|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|=a+b﹣c+2a﹣2b﹣2c+a+b+c=4a﹣2c.
18.证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°.
在△ABD和△ACE中,,
∴△ABD≌△ACE(AAS).
∴BD=CE.
19.解:∵CE平分∠ACB,∠ACB=80°,
∴,∠A+∠B=180°﹣80°=100°.
∵∠A比∠B大20°,
∴∠A﹣∠B=20°,
∴∠A=60°,∠B=40°,
∵CD是AB边上的高,
∴∠CDA=90°,
∴∠ACD=90°﹣∠A=30°,
∴∠DCE=∠ACE﹣∠ACD
=40°﹣30°
=10°.
20.证明:∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AC=DF,
在△AOC和△DOF中,
,
∴△AOC≌△DOF(AAS)
∴AO=DO,FO=CO,
∵BF=CE,
∴BO=EO,
∴AD与BE互相平分.
21.证明:∵BD、CE分别是AC、AB边上的高,
∴∠ADB=90°,∠AEC=90°,
∴∠ABQ+∠BAD=90°,∠BAC+∠ACE=90°,
∴∠ABD=∠ACE,
在△ABQ和△FCA中,
∴△ABQ≌△FCA(SAS),
∴∠F=∠BAQ,
∵∠F+∠FAE=90°,
∴∠BAQ+∠FAE=90°,
∴AF⊥AQ.
22.证明:(1)①∵∠ADC=∠ACB=∠BEC=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠CBE=90°,∠ACD+∠BCE=90°.
∴∠CAD=∠BCE.
∵AC=BC,
∴△ADC≌△CEB.
②∵△ADC≌△CEB,
∴CE=AD,CD=BE.
∴DE=CE+CD=AD+BE.
解:(2)∵∠ADC=∠CEB=∠ACB=90°,
∴∠ACD=∠CBE.
又∵AC=BC,
∴△ACD≌△CBE.
∴CE=AD,CD=BE.
∴DE=CE﹣CD=AD﹣BE.
(3)当MN旋转到图3的位置时,AD、DE、BE所满足的等量关系是DE=BE﹣AD(或AD=BE﹣DE,BE=AD+DE等).
∵∠ADC=∠CEB=∠ACB=90°,
∴∠ACD=∠CBE,
又∵AC=BC,
∴△ACD≌△CBE,
∴AD=CE,CD=BE,
∴DE=CD﹣CE=BE﹣AD.
一.选择题(共8小题,满分32分)
1.用三根长分别为3cm,6cm,acm的小木棒首尾相接拼成一个三角形,则a可能是( )
A.1 B.2 C.3 D.4
2.若正多边形的内角和是1080°,则该正多边形的一个外角为( )
A.45° B.60° C.72° D.90°
3.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )
A.相等 B.互余 C.互补或相等 D.不相等
4.如图,已知BP是∠ABC的平分线,AP⊥BP,若,则△ABC的面积等于( )
A.24cm2 B.30cm2 C.36cm2 D.不能确定
5.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62° B.56° C.34° D.124°
6.在下列△ABC中,正确画出AC边上的高的图形是( )
A. B.
C. D.
7.如图,在△ABC中,将CA沿DE翻折,点A落在F处,∠CEF、∠BDF、∠A三者之间的关系是( )
A.∠CEF=∠BDF+∠A B.∠CEF﹣3∠A=∠BDF
C.∠CEF=2(∠BDF+∠A) D.∠CEF﹣∠BDF=2∠A
8.如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.其中正确的结论是( )
A.②③④ B.①③④ C.①②④ D.①②③
二.填空题(共8小题,满分32分)
9.空调外机安装在墙壁上时,一般都会像如图所示的方法固定在墙壁上,这种方法是利用了三角形的 .
10.在△ABC中,若∠A:∠B:∠C=5:8:13,则这个三角形按角分类是 三角形.
11.如图,AE是∠BAD的平分线,CE是∠BCD的平分线,且AE与CE相交于点E.若∠D=40°,∠B=30°,则∠E的度数为 .
12.如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 °.
13.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是 .
14.如图,在△ABC中,AD为BC边的中线,E为AD上一点,连接BE并延长交AC于点F,若∠AEF=∠FAE,BE=4,EF=1.6,则CF的长为 .
15.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE= cm.
16.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= .
三.解答题(共6小题,满分56分)
17.已知三角形的三边长分别为a,b,c,化简:|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|.
18.如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.求证:BD=CE.
19.如图,在△ABC中,CD是AB边上的高,CE平分∠ACB.若∠ACB=80°,∠A比∠B大20°,求∠DCE的度数.
20.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分.
21.已知:△ABC中,BD、CE分别是AC、AB边上的高,BQ=AC,点F在CE的延长线上,CF=AB,求证:AF⊥AQ.
22.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
参考答案
一.选择题(共8小题,满分32分)
1.解:由三角形的三边关系可知:6﹣3<a<6+3,即3<a<9,
则a可能是4,
故选:D.
2.解:设这个正多边形的边数为n,
∵一个正多边形的内角和为1080°,
∴180(n﹣2)=1080,
解得:n=8,
∴这个正多边形的每一个外角是:360°÷8=45°.
故选:A.
3.解:第一种情况,当两个三角形全等时,是相等关系,
第二种情况,如图,AC=AC′,高CD=C′D′,
∴∠ADC=∠AD′C′,
在Rt△ACD和Rt△AC′D′中,
Rt△ACD≌Rt△AC′D′(HL),
∴∠CAD=∠C′AD′,
此时,∠CAB+∠C′AB=180°,
是互补关系,
所以选“相等或互补”.
故选:C.
4.解:延长AP交BC于点D,
∵BP是∠ABC的平分线,
∴∠ABP=∠DBP,
∵AP⊥BP,
∴∠APB=∠DPB=90°,
∵BP=BP,
∴△BAP≌△BDP(ASA),
∴AP=DP,
∴△APC的面积=△DPC的面积,
∵△BPC的面积=12cm2,
∴△BPD的面积+△CPD的面积=12,
∴△ABP的面积+△APC的面积=12,
∴△ABC的面积=24cm2,
故选:A.
5.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
6.解:A、AD不是AC边上的高,不符合题意;
B、AD是BC边上的高,不是AC边上的高,不符合题意;
C、BD不是AC边上的高,不符合题意;
D、BD是AC边上的高,符合题意;
故选:D.
7.解:如图,
∵∠CEF=∠A+∠AOE,∠AOE=∠F+∠BDF,
∴∠CEF=∠A+∠F+∠BDF,
由折叠性质可得:
∠A=∠F,
∴∠CEF=2∠A+∠BDF,
∴∠CEF﹣∠BDF=2∠A,
故选:D.
8.解:∵∠BAC=90°,AD⊥BC,
∴∠C+∠ABC=90°,
∠BAD+∠ABC=90°,
∴∠BAD=∠C,故①正确;
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,
∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
又∵∠AFE=∠BFD(对顶角相等),
∴∠AEF=∠AFE,故②正确;
∵∠ABE=∠CBE,
∴只有∠C=30°时∠EBC=∠C,故③错误;
∵∠AEF=∠AFE,
∴AE=AF,
∵AG平分∠DAC,
∴AG⊥EF,故④正确.
综上所述,正确的结论是①②④.
故选:C.
二.填空题(共8小题,满分32分)
9.解:这种方法应用的数学知识是:三角形的稳定性,
故答案为:稳定性.
10.解:∵∠A:∠B:∠C=5:8:13,
∴.
∴这个三角形是直角三角形.
故答案为:直角.
11.解:∵AE是∠BAD的平分线,CE是∠BCD的平分线,
∴∠DAE=∠DAB,∠DAE=∠DAB,
∵∠D+∠DCB=∠B+∠BAD①,∠D=40°,∠B=30°,
∴∠BAD﹣∠DCB=10°,
∴∠DAE﹣∠DCE=5°,
∵∠D+∠DCE=∠E+∠DAE②,
①+②,得80°+3∠DCE=30°+∠E+3∠DAE,
∴50°﹣3(∠DAE﹣∠DCE)=∠E,
∴∠E=35°,
故答案为:35°.
12.解:∵△ABC≌△ADE,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠BAD=40°,
∴∠ABD=∠ADB=(180°﹣∠BAD)=70°,
∵△ABC≌△ADE,
∴∠ADE=∠ABD=70°,
∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=114°﹣40°=74°,
∴∠E=180°﹣∠ADE﹣∠DAE=180°﹣70°﹣74°=36°,
故答案为:36.
13.解:过A点作AF⊥CD交CD的延长线于F点,如图,
∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠3,
在△ABE和△ADF中,
∵,
∴△ABE≌△ADF(AAS),
∴AE=AF=3,S△ABE=S△ADF,
∴四边形AECF是边长为3的正方形,
∴S四边形ABCD=S正方形AECF=32=9.
故答案为:9.
14.解:如图,延长AD至G,使DG=AD,连接BG,
在△BDG和△CDA中,
,
∴△BDG≌△CDA(SAS),
∴BG=AC,∠CAD=∠G,
∵∠AEF=∠FAE,
∴∠CAD=∠AEF,
∵∠BEG=∠AEF,
∴∠CAD=∠BEG,
∴∠G=∠BEG,
∴BG=BE=4,
∴AC=BE=4,
∵∠AEF=∠FAE,
∴AF=EF=1.6,
∴CF=AC﹣AF=4﹣1.6=2.4.
故答案为:2.4.
15.解:∵BE⊥CE,AD⊥CE
∴∠E=∠ADC=90°
∴∠DAC+∠DCA=90°
∵∠ACB=90°
∴∠BCE+∠DCA=90°
∴∠DAC=∠BCE
在△ACD和△CBE中,
,
∴△ACD≌△CBE
∴BE=CD=0.5(cm),EC=AD=2(cm)
DE=CE﹣CD=1.5(cm),
故答案为1.5
16.解:∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠3=∠ACB,
∵∠ACB+∠1=90°,
∴∠1+∠3=90°,
∴∠1+∠2+∠3=90°+45°=135°,
故答案为:135°.
三.解答题(共6小题,满分56分)
17.解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,则a+b﹣c>0,a﹣b﹣c<0,a+b+c>0,
∴|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|=a+b﹣c+2a﹣2b﹣2c+a+b+c=4a﹣2c.
18.证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°.
在△ABD和△ACE中,,
∴△ABD≌△ACE(AAS).
∴BD=CE.
19.解:∵CE平分∠ACB,∠ACB=80°,
∴,∠A+∠B=180°﹣80°=100°.
∵∠A比∠B大20°,
∴∠A﹣∠B=20°,
∴∠A=60°,∠B=40°,
∵CD是AB边上的高,
∴∠CDA=90°,
∴∠ACD=90°﹣∠A=30°,
∴∠DCE=∠ACE﹣∠ACD
=40°﹣30°
=10°.
20.证明:∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AC=DF,
在△AOC和△DOF中,
,
∴△AOC≌△DOF(AAS)
∴AO=DO,FO=CO,
∵BF=CE,
∴BO=EO,
∴AD与BE互相平分.
21.证明:∵BD、CE分别是AC、AB边上的高,
∴∠ADB=90°,∠AEC=90°,
∴∠ABQ+∠BAD=90°,∠BAC+∠ACE=90°,
∴∠ABD=∠ACE,
在△ABQ和△FCA中,
∴△ABQ≌△FCA(SAS),
∴∠F=∠BAQ,
∵∠F+∠FAE=90°,
∴∠BAQ+∠FAE=90°,
∴AF⊥AQ.
22.证明:(1)①∵∠ADC=∠ACB=∠BEC=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠CBE=90°,∠ACD+∠BCE=90°.
∴∠CAD=∠BCE.
∵AC=BC,
∴△ADC≌△CEB.
②∵△ADC≌△CEB,
∴CE=AD,CD=BE.
∴DE=CE+CD=AD+BE.
解:(2)∵∠ADC=∠CEB=∠ACB=90°,
∴∠ACD=∠CBE.
又∵AC=BC,
∴△ACD≌△CBE.
∴CE=AD,CD=BE.
∴DE=CE﹣CD=AD﹣BE.
(3)当MN旋转到图3的位置时,AD、DE、BE所满足的等量关系是DE=BE﹣AD(或AD=BE﹣DE,BE=AD+DE等).
∵∠ADC=∠CEB=∠ACB=90°,
∴∠ACD=∠CBE,
又∵AC=BC,
∴△ACD≌△CBE,
∴AD=CE,CD=BE,
∴DE=CD﹣CE=BE﹣AD.
