1.4 用一元二次方程解决问题 同步练习(含答案)2023-2024学年苏科版数学九年级上册
文档属性
| 名称 | 1.4 用一元二次方程解决问题 同步练习(含答案)2023-2024学年苏科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 49.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 20:51:20 | ||
图片预览

文档简介
1.4 用一元二次方程解决问题
一、单选题
1.用一条长为的绳子围成一个面积为的长方形,a的值不可能为( )
A.120 B.100 C.60 D.20
2.十年后,2003班学生聚会,见面时相互间均握了一次手,好事者统计:一共握了780次.你认为这次聚会的同学有( )人。
A.38 B.39 C.40 D.41
3.某农场2020年蔬菜产量为50吨,2022年蔬菜产量为60.5吨,该农场蔬菜产量的年平均增长率相同.设该农场蔬菜产量的年平均增长率为 ,则根据题意可列方程为( )
A. B.
C. D.
4.某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排21场比赛,则八年级班级的个数为( )
A.5 B.6 C.7 D.8
5.在某中学开展的课外阅读活动中,要求七,八、九三个年级学生的人均阅读量逐次增加,而且增长率相同,已知七年级学生的人均阅读量为每年10万字,九年级学生的人均阅读量为每年14.4万字,则该校八年级学生的人均阅读量为每年( )
A.11万字 B.11.2万字 C.12万字 D.12.2万字
6.随着科技水平的提高,某种电子产品的价格呈下降趋势,今年年底的价格是两年前价格的.这种电子产品的价格在这两年中平均每年下降百分之几?( )
A.25% B.37.5% C.50% D.75%
7.某校“研学”活动小组在一次野外实践时,发现一种植物的个主干上长出个枝干,每个枝干上再长出个小分支若在一个主干上的主干,枝干和小分支的数量之和是个,则等于( )
A. B. C. D.
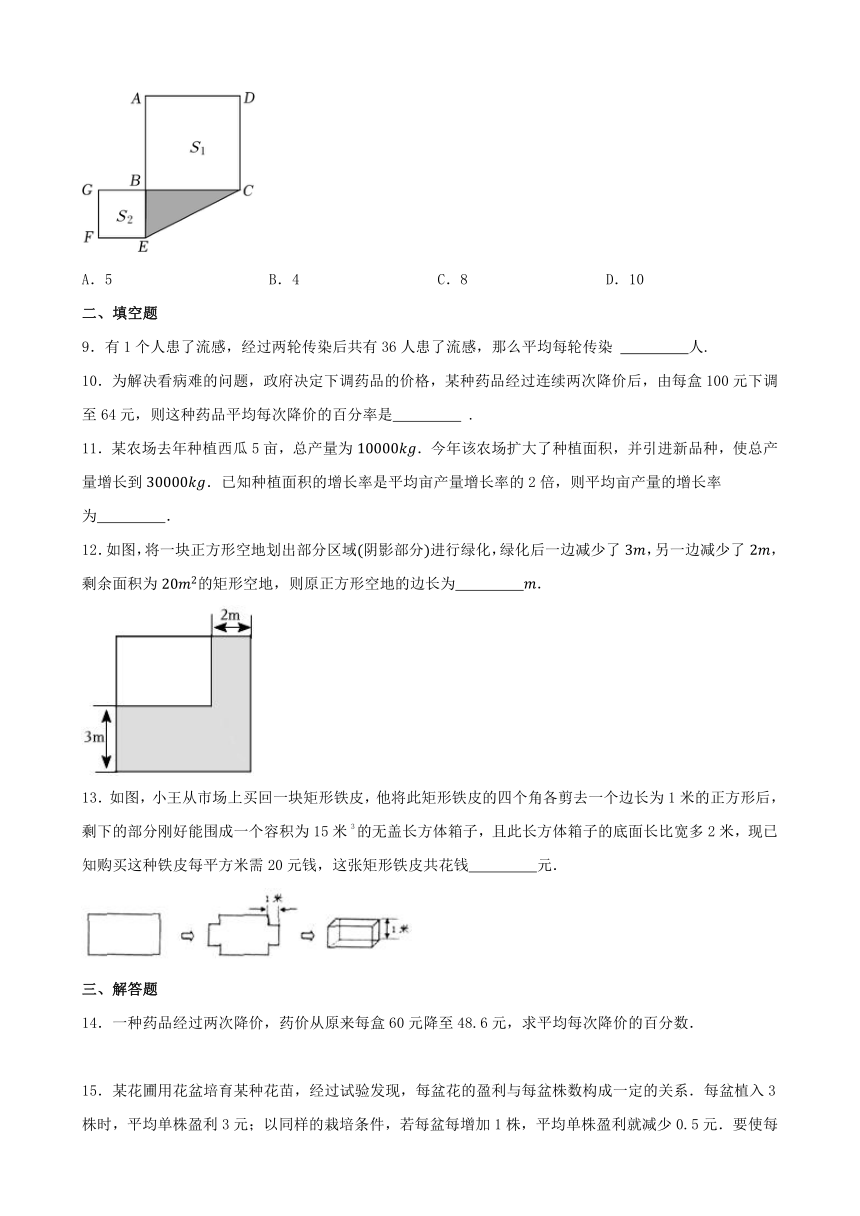
8.如图,两个正方形的泳池,面积分别是和,两个泳池的面积之和,点是线段上一点,设,在阴影部分铺上防滑瓷砖,则所需防滑瓷砖的面积为( )
A.5 B.4 C.8 D.10
二、填空题
9.有1个人患了流感,经过两轮传染后共有36人患了流感,那么平均每轮传染 人.
10.为解决看病难的问题,政府决定下调药品的价格,某种药品经过连续两次降价后,由每盒100元下调至64元,则这种药品平均每次降价的百分率是 .
11.某农场去年种植西瓜5亩,总产量为.今年该农场扩大了种植面积,并引进新品种,使总产量增长到.已知种植面积的增长率是平均亩产量增长率的2倍,则平均亩产量的增长率为 .
12.如图,将一块正方形空地划出部分区域阴影部分进行绿化,绿化后一边减少了,另一边减少了,剩余面积为的矩形空地,则原正方形空地的边长为 .
13.如图,小王从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15米3的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,这张矩形铁皮共花钱 元.
三、解答题
14.一种药品经过两次降价,药价从原来每盒60元降至48.6元,求平均每次降价的百分数.
15.某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利为10元,则每盆应植多少株
16.如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若草坪部分总面积为112m2,求小路的宽.
17.云南某店销售某品牌置物架,平时每天平均可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店在“双十一”期间采取了降价促销措施,在每件盈利不少于27元的前提下,经过一段时间销售,发现销售单价每降低4元,平均每天可多售出8件.
(1)若降价3元,则平均每天的销售数量为 件.
(2)当每个置物架降价多少元时,该商店每天销售利润为1200元?
18.某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售有如下关系,若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售一部,所有出售的汽车的进价均降低0.1万元/部.月底厂家根据销售量一次性返利给销售公司,销售量在10部以内,含10部,每部返利0.5万元,销售量在10部以上,每部返利1万元.
(1)若该公司当月卖出3部汽车,求每部汽车的进价是多少万元;
(2)如果汽车的销售价位28万元/部,该公司计划当月盈利12万元,那么要卖出
多少部汽车?(盈利=销售利润+返利)
参考答案
1.A
2.C
3.C
4.C
5.C
6.C
7.C
8.A
9.5
10.20%
11.50%
12.7
13.700
14.解:设平均每次降价的百分数为x
根据题意得: ,
解得: , (舍去).
答:平均每次降价的百分数为 .
15.解:设每盆花苗增加x株,则每盆花苗有(3+x)株,平均单株盈利为(3-0.5x)元.由题意,得(x+3)(3-0.5x)=10.
化简、整理,得x2-3x+2= 0.解这个方程,得x1=1,x2 =2.
经检验,x1=1,x2 =2都是方程的解,且符合题意.
答:要使每盆的盈利为10元,则每盆应植入4株或5株.
16.解:设小路的宽度为xm,那么整个草坪的长为(16﹣2x)m,宽为(9﹣x)m.根据题意得:
(16﹣2x)(9﹣x)=112
解得:x1=1,x2=16.
∵16>9,∴x=16不符合题意,舍去,∴x=1.
答:小路的宽为1m.
17.(1)26
(2)解:设每个置物架降价x元时,该商店每天销售利润为1200元.
根据题意,得 (40﹣x)(20+2x)=1200,
整理,得x2﹣30x+200=0,
解得:x1=10,x2=20.
∵要求每件盈利不少于27元,40-20=20<27,
∴x2=20应舍去,
解得:x=10.
答:每个置物架应降价10元时,该商店每天销售利润为1200元.
18.(1)解:27-0.1×(3-1)=26.8
(2)解:设需要售出x部汽车,由题意可知,每部汽车的销售利润为:
28-[27-0.1(x-1)] =(0.1x+0.9)(万元),
当0≤x≤10,根据题意,得x(0.1x+0.9)+0.5x=12,
整理,得x2+14x-120=0,
解这个方程,得x1=-20(不合题意,舍去),x2=6.
当x>10时,根据题意,得x(0.1x+0.9)+x=12,
整理,得x2+19x-120=0,
解这个方程,得x1=-24(不合题意,舍去),x2=5.
∵5<10,∴x2=5舍去.
答:要卖出6部汽车
一、单选题
1.用一条长为的绳子围成一个面积为的长方形,a的值不可能为( )
A.120 B.100 C.60 D.20
2.十年后,2003班学生聚会,见面时相互间均握了一次手,好事者统计:一共握了780次.你认为这次聚会的同学有( )人。
A.38 B.39 C.40 D.41
3.某农场2020年蔬菜产量为50吨,2022年蔬菜产量为60.5吨,该农场蔬菜产量的年平均增长率相同.设该农场蔬菜产量的年平均增长率为 ,则根据题意可列方程为( )
A. B.
C. D.
4.某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排21场比赛,则八年级班级的个数为( )
A.5 B.6 C.7 D.8
5.在某中学开展的课外阅读活动中,要求七,八、九三个年级学生的人均阅读量逐次增加,而且增长率相同,已知七年级学生的人均阅读量为每年10万字,九年级学生的人均阅读量为每年14.4万字,则该校八年级学生的人均阅读量为每年( )
A.11万字 B.11.2万字 C.12万字 D.12.2万字
6.随着科技水平的提高,某种电子产品的价格呈下降趋势,今年年底的价格是两年前价格的.这种电子产品的价格在这两年中平均每年下降百分之几?( )
A.25% B.37.5% C.50% D.75%
7.某校“研学”活动小组在一次野外实践时,发现一种植物的个主干上长出个枝干,每个枝干上再长出个小分支若在一个主干上的主干,枝干和小分支的数量之和是个,则等于( )
A. B. C. D.
8.如图,两个正方形的泳池,面积分别是和,两个泳池的面积之和,点是线段上一点,设,在阴影部分铺上防滑瓷砖,则所需防滑瓷砖的面积为( )
A.5 B.4 C.8 D.10
二、填空题
9.有1个人患了流感,经过两轮传染后共有36人患了流感,那么平均每轮传染 人.
10.为解决看病难的问题,政府决定下调药品的价格,某种药品经过连续两次降价后,由每盒100元下调至64元,则这种药品平均每次降价的百分率是 .
11.某农场去年种植西瓜5亩,总产量为.今年该农场扩大了种植面积,并引进新品种,使总产量增长到.已知种植面积的增长率是平均亩产量增长率的2倍,则平均亩产量的增长率为 .
12.如图,将一块正方形空地划出部分区域阴影部分进行绿化,绿化后一边减少了,另一边减少了,剩余面积为的矩形空地,则原正方形空地的边长为 .
13.如图,小王从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15米3的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,这张矩形铁皮共花钱 元.
三、解答题
14.一种药品经过两次降价,药价从原来每盒60元降至48.6元,求平均每次降价的百分数.
15.某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利为10元,则每盆应植多少株
16.如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若草坪部分总面积为112m2,求小路的宽.
17.云南某店销售某品牌置物架,平时每天平均可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店在“双十一”期间采取了降价促销措施,在每件盈利不少于27元的前提下,经过一段时间销售,发现销售单价每降低4元,平均每天可多售出8件.
(1)若降价3元,则平均每天的销售数量为 件.
(2)当每个置物架降价多少元时,该商店每天销售利润为1200元?
18.某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售有如下关系,若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售一部,所有出售的汽车的进价均降低0.1万元/部.月底厂家根据销售量一次性返利给销售公司,销售量在10部以内,含10部,每部返利0.5万元,销售量在10部以上,每部返利1万元.
(1)若该公司当月卖出3部汽车,求每部汽车的进价是多少万元;
(2)如果汽车的销售价位28万元/部,该公司计划当月盈利12万元,那么要卖出
多少部汽车?(盈利=销售利润+返利)
参考答案
1.A
2.C
3.C
4.C
5.C
6.C
7.C
8.A
9.5
10.20%
11.50%
12.7
13.700
14.解:设平均每次降价的百分数为x
根据题意得: ,
解得: , (舍去).
答:平均每次降价的百分数为 .
15.解:设每盆花苗增加x株,则每盆花苗有(3+x)株,平均单株盈利为(3-0.5x)元.由题意,得(x+3)(3-0.5x)=10.
化简、整理,得x2-3x+2= 0.解这个方程,得x1=1,x2 =2.
经检验,x1=1,x2 =2都是方程的解,且符合题意.
答:要使每盆的盈利为10元,则每盆应植入4株或5株.
16.解:设小路的宽度为xm,那么整个草坪的长为(16﹣2x)m,宽为(9﹣x)m.根据题意得:
(16﹣2x)(9﹣x)=112
解得:x1=1,x2=16.
∵16>9,∴x=16不符合题意,舍去,∴x=1.
答:小路的宽为1m.
17.(1)26
(2)解:设每个置物架降价x元时,该商店每天销售利润为1200元.
根据题意,得 (40﹣x)(20+2x)=1200,
整理,得x2﹣30x+200=0,
解得:x1=10,x2=20.
∵要求每件盈利不少于27元,40-20=20<27,
∴x2=20应舍去,
解得:x=10.
答:每个置物架应降价10元时,该商店每天销售利润为1200元.
18.(1)解:27-0.1×(3-1)=26.8
(2)解:设需要售出x部汽车,由题意可知,每部汽车的销售利润为:
28-[27-0.1(x-1)] =(0.1x+0.9)(万元),
当0≤x≤10,根据题意,得x(0.1x+0.9)+0.5x=12,
整理,得x2+14x-120=0,
解这个方程,得x1=-20(不合题意,舍去),x2=6.
当x>10时,根据题意,得x(0.1x+0.9)+x=12,
整理,得x2+19x-120=0,
解这个方程,得x1=-24(不合题意,舍去),x2=5.
∵5<10,∴x2=5舍去.
答:要卖出6部汽车
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
