第22章 二次函数 单元达标测试题(含解析)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 第22章 二次函数 单元达标测试题(含解析)2023-2024学年人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 314.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 21:03:31 | ||
图片预览



文档简介
2023-2024学年人教版九年级数学上册《第22章二次函数》单元达标测试题(附答案)
一、单选题(满分32分)
1.下列函数属于二次函数的是( )
A. B. C. D.
2.关于二次函数的图象与性质,下列结论错误的是( )
A.抛物线开口方向向下 B.当时,函数有最大值
C.当时,随的增大而减小 D.该抛物线可由经过平移得到
3.在平面直角坐标系中,抛物线向左平移3个单位,再向下平移3个单位,所得新的抛物线的顶点坐标为( )
A. B. C. D.
4.将二次函数化为的形式,结果为( )
A. B.
C. D.
5.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为、若此炮弹在第8秒与第16秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
6.抛物线:与抛物线:关于x轴对称,则抛物线的表达式是( )
A. B. C. D.
7.如图,抛物线的对称轴为直线,如果关于x的方程的一个根为,那么该方程的另一个根为( )
A.-2 B.-1 C.0 D.3
8.如图,抛物线与直线相交于,两点,则当时,自变量x的取值范围是( ).
A. B.
C.或 D.或
二、填空题(满分32分)
9.抛物线的对称轴是直线 .
10.已知抛物线 与x轴交于点、两点,则B点的横坐标= .
11.已知关于x的二次函数的图像与x轴总有交点,则m的取值范围是 .
12.将抛物线向下平移1个单位长度,再向右平移 个单位长度后,得到的新抛物线经过原点.
13.如图,用长为的篱笆,一边利用墙(墙足够长)围成一个长方形花园,设花园的宽为,围成的花圃面积为,则y关于x的函数表达式为 .
14.如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是,则铅球推出的距离 m.
15.已知抛物线与直线分别交于A,C两点,直线与直线关于抛物线的对称轴对称,且直线与抛物线分别交于B,D两点,其中A,D两点在x轴上方,B,C两点在x轴下方.若,则m的值为 .
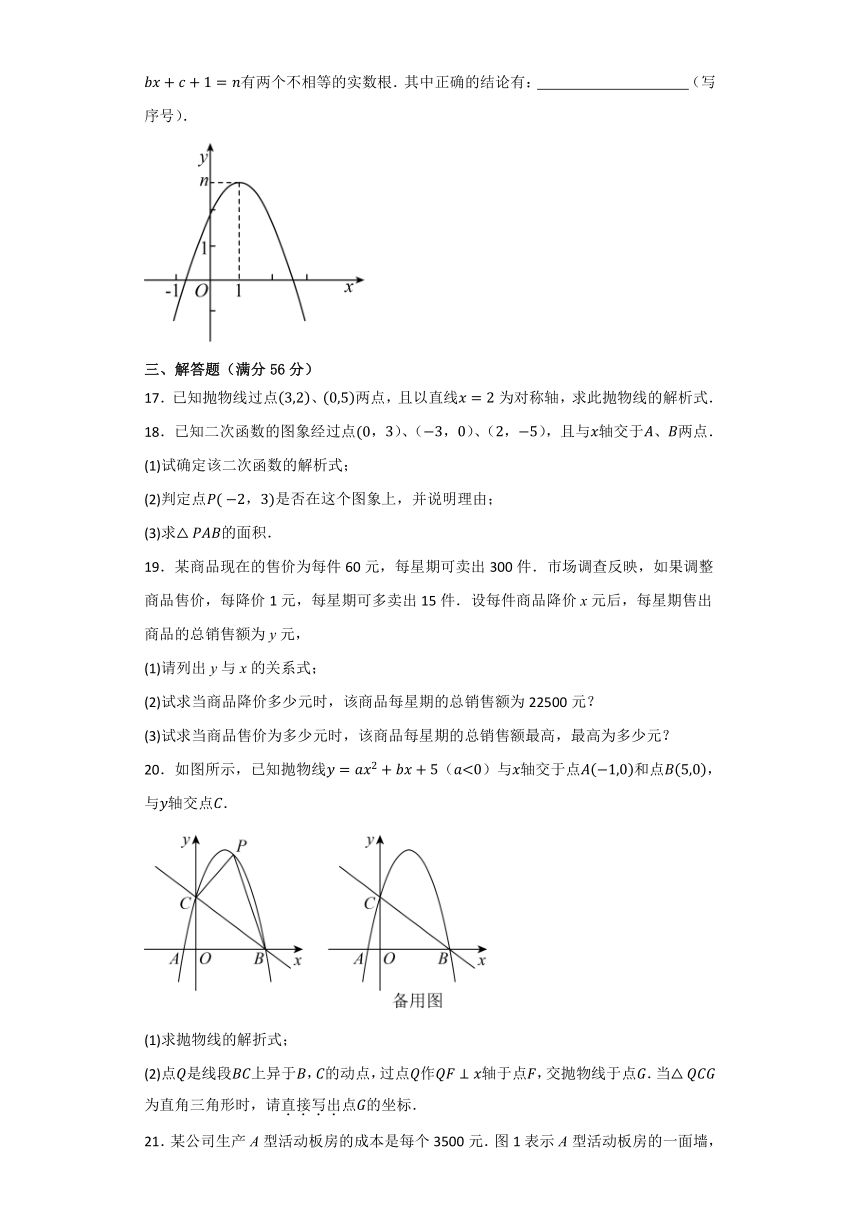
16.如图,二次函数的图象的顶点坐标为,则以下五个结论中:①,②,③,④,⑤方程有两个不相等的实数根.其中正确的结论有: (写序号).
三、解答题(满分56分)
17.已知抛物线过点、两点,且以直线为对称轴,求此抛物线的解析式.
18.已知二次函数的图象经过点,)、(,)、(,),且与轴交于、两点.
(1)试确定该二次函数的解析式;
(2)判定点 ,是否在这个图象上,并说明理由;
(3)求的面积.
19.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出15件.设每件商品降价x元后,每星期售出商品的总销售额为y元,
(1)请列出y与x的关系式;
(2)试求当商品降价多少元时,该商品每星期的总销售额为22500元?
(3)试求当商品售价为多少元时,该商品每星期的总销售额最高,最高为多少元?
20.如图所示,已知抛物线()与轴交于点和点,与轴交点.
(1)求抛物线的解折式;
(2)点是线段上异于,的动点,过点作轴于点,交抛物线于点.当为直角三角形时,请直接写出点的坐标.
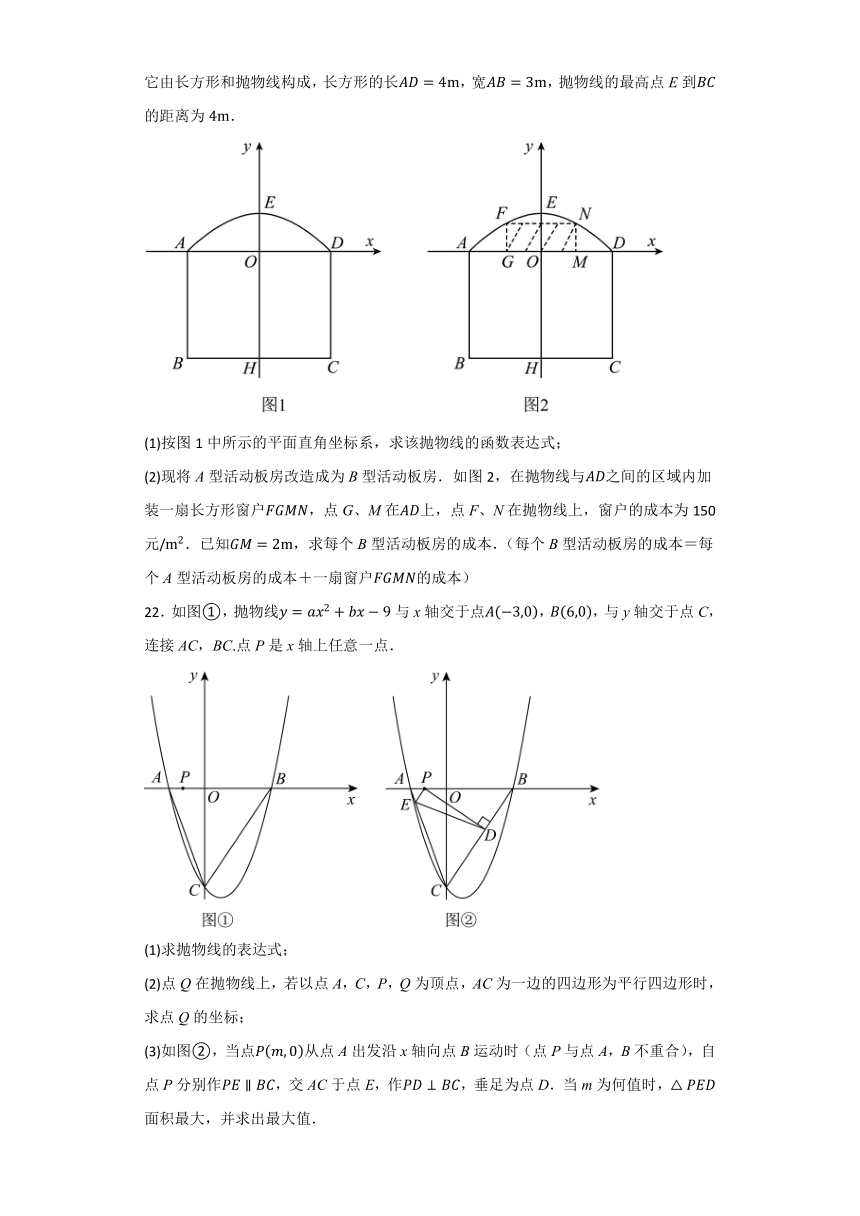
21.某公司生产A型活动板房的成本是每个3500元.图1表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长,宽,抛物线的最高点E到的距离为.
(1)按图1中所示的平面直角坐标系,求该抛物线的函数表达式;
(2)现将A型活动板房改造成为B型活动板房.如图2,在抛物线与之间的区域内加装一扇长方形窗户,点G、M在上,点F、N在抛物线上,窗户的成本为150元/.已知,求每个B型活动板房的成本.(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户的成本)
22.如图①,抛物线与x轴交于点,,与y轴交于点C,连接AC,BC.点P是x轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;
(3)如图②,当点从点A出发沿x轴向点B运动时(点P与点A,B不重合),自点P分别作,交AC于点E,作,垂足为点D.当m为何值时,面积最大,并求出最大值.
参考答案
1.解:A、是一次函数,不是二次函数,故本选项不符合题意;
B、符合二次函数的定义,故本选项符合题意;
C、,是一次函数,不是二次函数,故本选项不符合题意;
D、的右边是分式,不是二次函数,故本选项不符合题意;
故选:B.
2.解:∵二次函数解析式为中,,
∴二次函数开口向下,对称轴为直线,故A结论正确,不符合题意;
∴当时,函数有最大值,当时,随的增大而减小,故B结论错误,符合题意,C结论正确,不符合题意;
抛物线向左移动3个单位长度,向下移动2个单位长度得到抛物线,故D结论正确,不符合题意;
故选B.
3.解:将抛物线顶点坐标为,向左平移3个单位长度,再向下平移3个单位长度,得到的抛物线的解析式是将抛物线,
故平移后的顶点坐标为.
故选:B.
4.解: ,
故选:A.
5.解:∵此炮弹在第8秒与第16秒时的高度相等,
∴抛物线的对称轴是:,
∴炮弹所在高度最高的是第12秒.
故选:C.
6.解:抛物线的顶点坐标为,而关于x轴对称的点的坐标为,所以所求抛物线的解析式为
故选:A
7.解:∵关于x的方程有一个根为4,
∴抛物线与x轴的一个交点为,
抛物线的对称轴为直线
抛物线的对称轴也是,
∴抛物线与x轴的另一个交点为
∴方程的另一个根为
故选:A.
8.解:由图象可知,当时,自变量x的取值范围是,
故选:A.
9.解:方法1:利用公式法
的顶点坐标公式为,代入数值求得对称轴是直线;
方法2:利用配方法
,故对称轴是直线.
故答案为:.
10.解:对称轴为直线,
抛物线与x轴交于点、两点,
点,
B点的横坐标.
故答案为:.
11.解:∵二次函数的图像与x轴总有交点,
∴且,
解得且,
故答案为:且.
12.解:抛物线向下平移1个单位长度后的解析式为,
令,则,
解得,,
∴抛物线与的交点坐标为和,
∴将抛物线向右平移2个单位或4个单位后,新抛物线经过原点.
故答案为:2或4.
13.解:由题意可知花圃的长为,
则,
故答案为:.
14.解:令,则,
解得:,,
∴,
故答案为:.
15.解:∵
∴抛物线开口向上,对称轴为:,
∵直线与直线关于抛物线的对称轴对称,
∴两点关于直线对称,两点关于直线对称,
∴,
∵,
∴,
设,,则,,
∴,
由解析式联立可得:,
∴,
由根与系数的关系可得,,
∴,即
∴
解得:
故答案为:
16.解:①抛物线开口方向向下,则,
抛物线对称轴位于轴右侧,则异号,即,
抛物线与轴交于正半轴,则,
,故①错误;
②抛物线对称轴为直线,
,即,故②正确;
③由交点的位置可得:,
,
,
,
,
,
,故③错误;
④由图象可知,当时,,
此时点在第三象限,
,
,
,故④正确;
⑤方程有两个相等的实数根,
,
,
方程为,
,
方程为有两个不相等的实数根,故⑤正确;
综上所述,正确的为②④⑤,
故答案为:②④⑤.
17.解:函数以直线为对称轴,
设二次函数解析式为,
把点、代入,可得,
,即.
18.解:(1)设二次函数为,把,、 ,、, 代入二次函数解析式,
得:,
解得.
∴二次函数的解析式为:;
(2)把代入解析式,可得:,所以点 ,在函数图象上.
(3)当,,
解得:,
∴,
又 ,,
∴.
19.(1)解:由题意可得:
;
(2)解:由题意可得:,
解得,,
当商品降价30元或10元时,该商品每星期的总销售额为22500元;
(3)解:配方可得:,
因为,
所以当时,y有最大值,最大值是24000元.
答:当商品售价为20元,y有最大值,最大值是24000元.
20.(1)解:∵()与轴交于点和点,
∴,解得:,
∴抛物线为:;
(2)如图,过作于,
由抛物线,当,则,
∴,而,
∴,
∴,而轴,
当,
∴
∴,
∵,,
设直线为,
∴,
解得:,
∴直线为,
设,则
∴,,
∴,
解得:,(不符合题意舍去)
∴,
当时,如图,
则关于抛物线的对称轴对称,,
∴,
解得:,(不符合题意舍去)
∴,
综上:或.
21.解:(1)∵长方形的长,宽,抛物线的最高点E到的距离为,
∴,
∴,
∴,
设该抛物线的函数表达式为,
把代入,得,
解得,
∴该抛物线的函数表达式为;
(2)∵,
∴,
当时,,
∴,,
∴,
∴(元),
所以,每个B型活动板房的成本为3725元.
22.解:(1)将,代入,得
,解得
∴抛物线解析式为:
(2)二次函数,当时,
∴点
设点,点,
当为边,为对角线时,
∵四边形为平行四边形,
∴,互相平分
∴解得,(舍去)或
点Q坐标;
当为边,为对角线时,
同理得,
解得,或,
∴
∴点Q坐标或
综上,点Q坐标,或或;
(3)如图,过点D作,过点E作,垂足为G,F,
∵,
∴
∴
∵
∴,同理可得
设直线的解析式为:
则,解得
∴直线:
同理由点,,可求得直线 :
设点,,
则,,,
中,,
∴,
中,
∴,解得,
∴
∵
∴;
中,
∴,解得,
∴
∵
∴
∴,
即.
∵
∴时,,有最大值,最大值为.
一、单选题(满分32分)
1.下列函数属于二次函数的是( )
A. B. C. D.
2.关于二次函数的图象与性质,下列结论错误的是( )
A.抛物线开口方向向下 B.当时,函数有最大值
C.当时,随的增大而减小 D.该抛物线可由经过平移得到
3.在平面直角坐标系中,抛物线向左平移3个单位,再向下平移3个单位,所得新的抛物线的顶点坐标为( )
A. B. C. D.
4.将二次函数化为的形式,结果为( )
A. B.
C. D.
5.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为、若此炮弹在第8秒与第16秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
6.抛物线:与抛物线:关于x轴对称,则抛物线的表达式是( )
A. B. C. D.
7.如图,抛物线的对称轴为直线,如果关于x的方程的一个根为,那么该方程的另一个根为( )
A.-2 B.-1 C.0 D.3
8.如图,抛物线与直线相交于,两点,则当时,自变量x的取值范围是( ).
A. B.
C.或 D.或
二、填空题(满分32分)
9.抛物线的对称轴是直线 .
10.已知抛物线 与x轴交于点、两点,则B点的横坐标= .
11.已知关于x的二次函数的图像与x轴总有交点,则m的取值范围是 .
12.将抛物线向下平移1个单位长度,再向右平移 个单位长度后,得到的新抛物线经过原点.
13.如图,用长为的篱笆,一边利用墙(墙足够长)围成一个长方形花园,设花园的宽为,围成的花圃面积为,则y关于x的函数表达式为 .
14.如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是,则铅球推出的距离 m.
15.已知抛物线与直线分别交于A,C两点,直线与直线关于抛物线的对称轴对称,且直线与抛物线分别交于B,D两点,其中A,D两点在x轴上方,B,C两点在x轴下方.若,则m的值为 .
16.如图,二次函数的图象的顶点坐标为,则以下五个结论中:①,②,③,④,⑤方程有两个不相等的实数根.其中正确的结论有: (写序号).
三、解答题(满分56分)
17.已知抛物线过点、两点,且以直线为对称轴,求此抛物线的解析式.
18.已知二次函数的图象经过点,)、(,)、(,),且与轴交于、两点.
(1)试确定该二次函数的解析式;
(2)判定点 ,是否在这个图象上,并说明理由;
(3)求的面积.
19.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出15件.设每件商品降价x元后,每星期售出商品的总销售额为y元,
(1)请列出y与x的关系式;
(2)试求当商品降价多少元时,该商品每星期的总销售额为22500元?
(3)试求当商品售价为多少元时,该商品每星期的总销售额最高,最高为多少元?
20.如图所示,已知抛物线()与轴交于点和点,与轴交点.
(1)求抛物线的解折式;
(2)点是线段上异于,的动点,过点作轴于点,交抛物线于点.当为直角三角形时,请直接写出点的坐标.
21.某公司生产A型活动板房的成本是每个3500元.图1表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长,宽,抛物线的最高点E到的距离为.
(1)按图1中所示的平面直角坐标系,求该抛物线的函数表达式;
(2)现将A型活动板房改造成为B型活动板房.如图2,在抛物线与之间的区域内加装一扇长方形窗户,点G、M在上,点F、N在抛物线上,窗户的成本为150元/.已知,求每个B型活动板房的成本.(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户的成本)
22.如图①,抛物线与x轴交于点,,与y轴交于点C,连接AC,BC.点P是x轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;
(3)如图②,当点从点A出发沿x轴向点B运动时(点P与点A,B不重合),自点P分别作,交AC于点E,作,垂足为点D.当m为何值时,面积最大,并求出最大值.
参考答案
1.解:A、是一次函数,不是二次函数,故本选项不符合题意;
B、符合二次函数的定义,故本选项符合题意;
C、,是一次函数,不是二次函数,故本选项不符合题意;
D、的右边是分式,不是二次函数,故本选项不符合题意;
故选:B.
2.解:∵二次函数解析式为中,,
∴二次函数开口向下,对称轴为直线,故A结论正确,不符合题意;
∴当时,函数有最大值,当时,随的增大而减小,故B结论错误,符合题意,C结论正确,不符合题意;
抛物线向左移动3个单位长度,向下移动2个单位长度得到抛物线,故D结论正确,不符合题意;
故选B.
3.解:将抛物线顶点坐标为,向左平移3个单位长度,再向下平移3个单位长度,得到的抛物线的解析式是将抛物线,
故平移后的顶点坐标为.
故选:B.
4.解: ,
故选:A.
5.解:∵此炮弹在第8秒与第16秒时的高度相等,
∴抛物线的对称轴是:,
∴炮弹所在高度最高的是第12秒.
故选:C.
6.解:抛物线的顶点坐标为,而关于x轴对称的点的坐标为,所以所求抛物线的解析式为
故选:A
7.解:∵关于x的方程有一个根为4,
∴抛物线与x轴的一个交点为,
抛物线的对称轴为直线
抛物线的对称轴也是,
∴抛物线与x轴的另一个交点为
∴方程的另一个根为
故选:A.
8.解:由图象可知,当时,自变量x的取值范围是,
故选:A.
9.解:方法1:利用公式法
的顶点坐标公式为,代入数值求得对称轴是直线;
方法2:利用配方法
,故对称轴是直线.
故答案为:.
10.解:对称轴为直线,
抛物线与x轴交于点、两点,
点,
B点的横坐标.
故答案为:.
11.解:∵二次函数的图像与x轴总有交点,
∴且,
解得且,
故答案为:且.
12.解:抛物线向下平移1个单位长度后的解析式为,
令,则,
解得,,
∴抛物线与的交点坐标为和,
∴将抛物线向右平移2个单位或4个单位后,新抛物线经过原点.
故答案为:2或4.
13.解:由题意可知花圃的长为,
则,
故答案为:.
14.解:令,则,
解得:,,
∴,
故答案为:.
15.解:∵
∴抛物线开口向上,对称轴为:,
∵直线与直线关于抛物线的对称轴对称,
∴两点关于直线对称,两点关于直线对称,
∴,
∵,
∴,
设,,则,,
∴,
由解析式联立可得:,
∴,
由根与系数的关系可得,,
∴,即
∴
解得:
故答案为:
16.解:①抛物线开口方向向下,则,
抛物线对称轴位于轴右侧,则异号,即,
抛物线与轴交于正半轴,则,
,故①错误;
②抛物线对称轴为直线,
,即,故②正确;
③由交点的位置可得:,
,
,
,
,
,
,故③错误;
④由图象可知,当时,,
此时点在第三象限,
,
,
,故④正确;
⑤方程有两个相等的实数根,
,
,
方程为,
,
方程为有两个不相等的实数根,故⑤正确;
综上所述,正确的为②④⑤,
故答案为:②④⑤.
17.解:函数以直线为对称轴,
设二次函数解析式为,
把点、代入,可得,
,即.
18.解:(1)设二次函数为,把,、 ,、, 代入二次函数解析式,
得:,
解得.
∴二次函数的解析式为:;
(2)把代入解析式,可得:,所以点 ,在函数图象上.
(3)当,,
解得:,
∴,
又 ,,
∴.
19.(1)解:由题意可得:
;
(2)解:由题意可得:,
解得,,
当商品降价30元或10元时,该商品每星期的总销售额为22500元;
(3)解:配方可得:,
因为,
所以当时,y有最大值,最大值是24000元.
答:当商品售价为20元,y有最大值,最大值是24000元.
20.(1)解:∵()与轴交于点和点,
∴,解得:,
∴抛物线为:;
(2)如图,过作于,
由抛物线,当,则,
∴,而,
∴,
∴,而轴,
当,
∴
∴,
∵,,
设直线为,
∴,
解得:,
∴直线为,
设,则
∴,,
∴,
解得:,(不符合题意舍去)
∴,
当时,如图,
则关于抛物线的对称轴对称,,
∴,
解得:,(不符合题意舍去)
∴,
综上:或.
21.解:(1)∵长方形的长,宽,抛物线的最高点E到的距离为,
∴,
∴,
∴,
设该抛物线的函数表达式为,
把代入,得,
解得,
∴该抛物线的函数表达式为;
(2)∵,
∴,
当时,,
∴,,
∴,
∴(元),
所以,每个B型活动板房的成本为3725元.
22.解:(1)将,代入,得
,解得
∴抛物线解析式为:
(2)二次函数,当时,
∴点
设点,点,
当为边,为对角线时,
∵四边形为平行四边形,
∴,互相平分
∴解得,(舍去)或
点Q坐标;
当为边,为对角线时,
同理得,
解得,或,
∴
∴点Q坐标或
综上,点Q坐标,或或;
(3)如图,过点D作,过点E作,垂足为G,F,
∵,
∴
∴
∵
∴,同理可得
设直线的解析式为:
则,解得
∴直线:
同理由点,,可求得直线 :
设点,,
则,,,
中,,
∴,
中,
∴,解得,
∴
∵
∴;
中,
∴,解得,
∴
∵
∴
∴,
即.
∵
∴时,,有最大值,最大值为.
同课章节目录
