新人教版就年级上册第二十三章旋转全章学案(北京市海淀区)(无答案)
文档属性
| 名称 | 新人教版就年级上册第二十三章旋转全章学案(北京市海淀区)(无答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 657.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-15 06:24:00 | ||
图片预览

文档简介
23.1图形的旋转1
初试能力
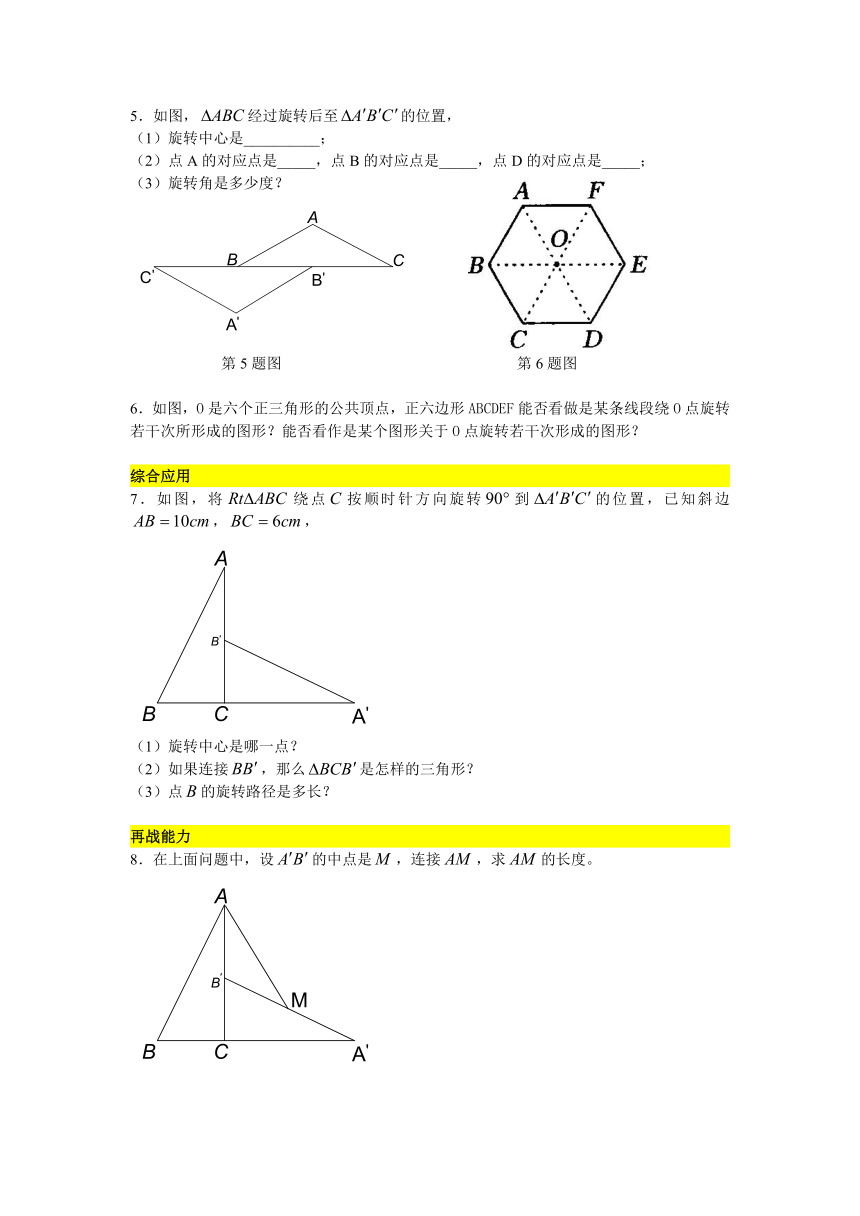
1.如图:ABC是等边三角形,D是BC上一点, ABD经过旋转后到达ACE的位置
(1)旋转中心是________,点A的对应点是_____,点B的对应点是_____,点D的对应点是_____;
(2)旋转了多少度?请标出一个旋转角;
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
第1题图 第2题图
2.如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置
(1)旋转中心是________,点A的对应点是_____,点B的对应点是_____,点D的对应点是_____;
(2)△ADP是___________三角形。
3.如图:P是等边ABC内的一点,把ABP按不同的方向通过旋转得到BQC和ACR,请问:
(1)怎样旋转ABP至BQC的位置?
旋转中心_________,旋转方向_________,旋转角度__________;
(2)怎样旋转ABP至ACR的位置?
旋转中心_________,旋转方向_________,旋转角度__________;
(3)ACR是否可以直接通过把BQC旋转得到?
第3题图 第4题图
能力提高
4.如图,如果正方形DCEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个,分别是_____________________________________________。
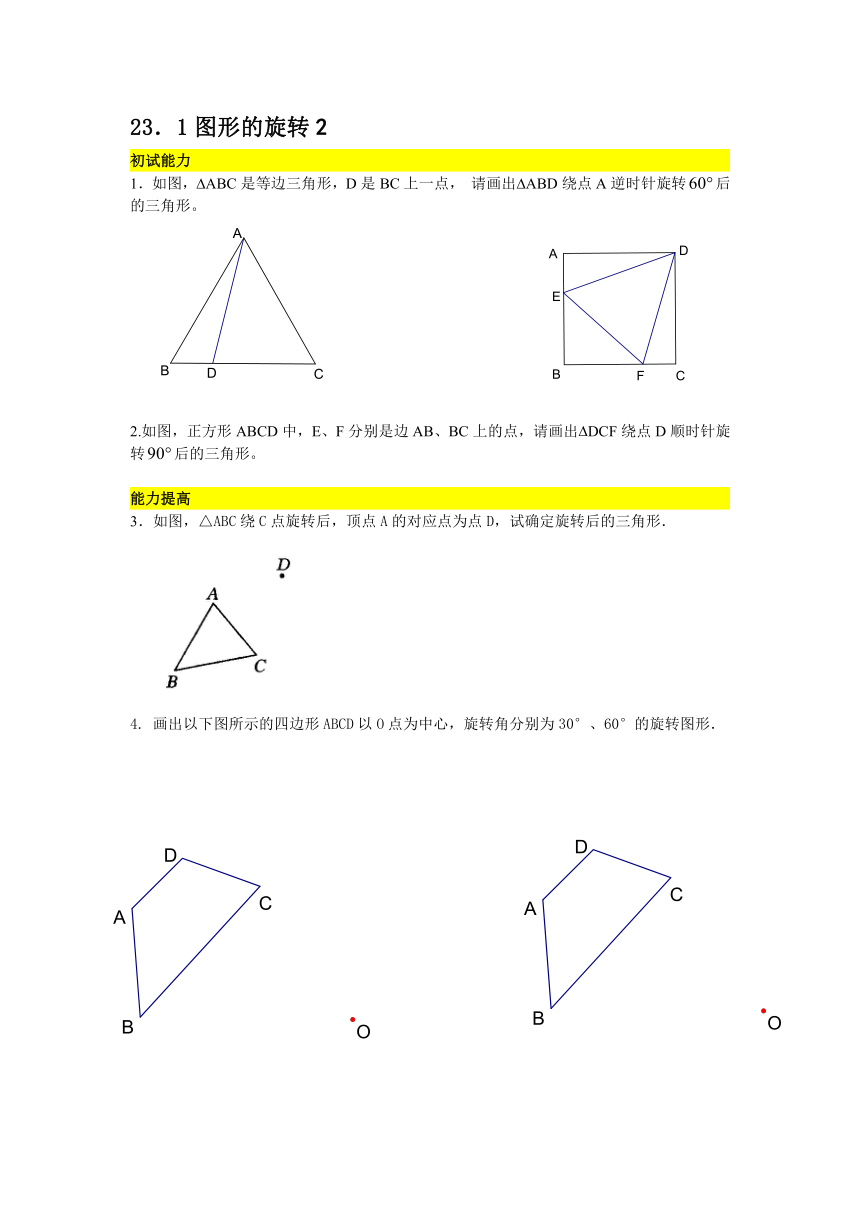
5.如图,经过旋转后至的位置,
(1)旋转中心是__________;
(2)点A的对应点是_____,点B的对应点是_____,点D的对应点是_____;
(3)旋转角是多少度?
第5题图 第6题图
6.如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形?能否看作是某个图形关于O点旋转若干次形成的图形?
综合应用
7.如图,将绕点按顺时针方向旋转到的位置,已知斜边,,
(1)旋转中心是哪一点?
(2)如果连接,那么是怎样的三角形?
(3)点的旋转路径是多长?
再战能力
8.在上面问题中,设的中点是,连接,求的长度。
23.1图形的旋转2
初试能力
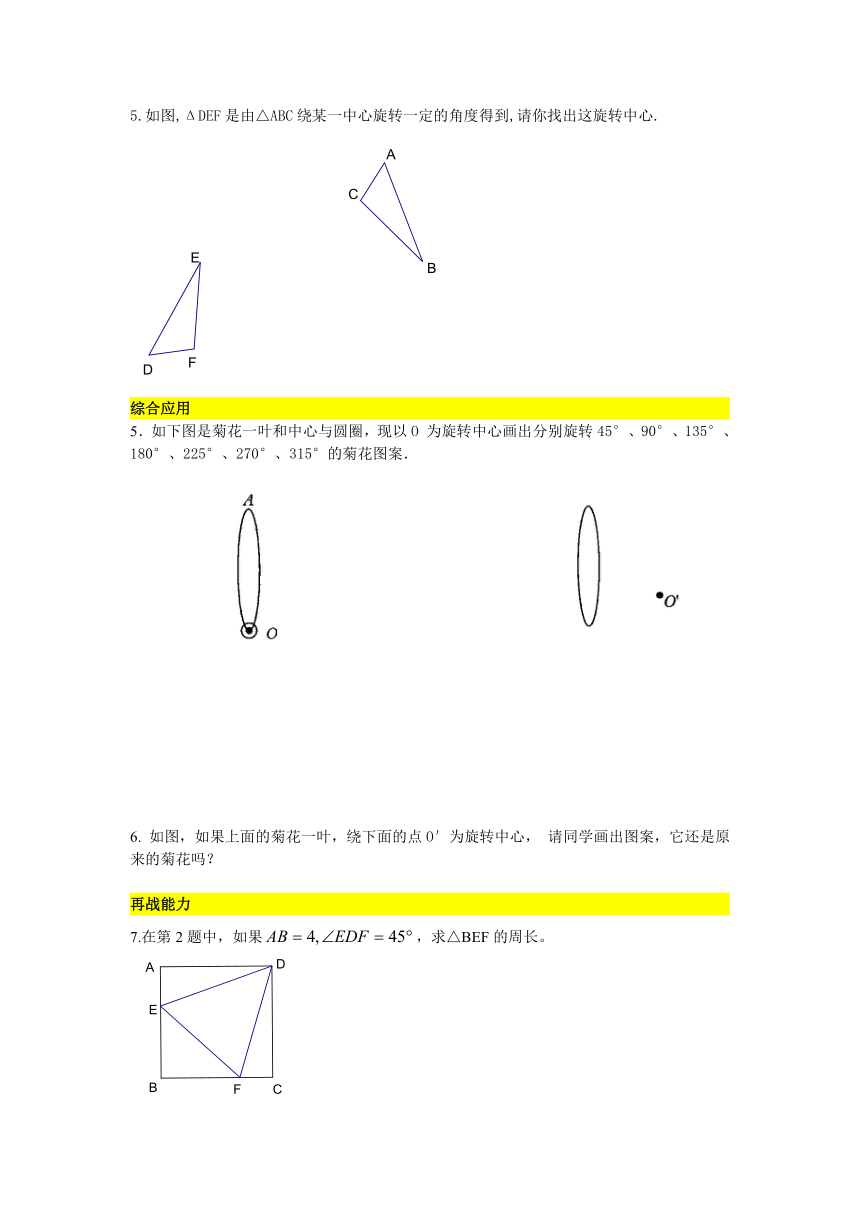
1.如图,ABC是等边三角形,D是BC上一点, 请画出ABD绕点A逆时针旋转后的三角形。
2.如图,正方形ABCD中,E、F分别是边AB、BC上的点,请画出DCF绕点D顺时针旋转后的三角形。
能力提高
3.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定旋转后的三角形.
4. 画出以下图所示的四边形ABCD以O点为中心,旋转角分别为30°、60°的旋转图形.
5.如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.
综合应用
5.如下图是菊花一叶和中心与圆圈,现以O为旋转中心画出分别旋转45°、90°、135°、180°、225°、270°、315°的菊花图案.
6. 如图,如果上面的菊花一叶,绕下面的点O′为旋转中心,请同学画出图案,它还是原来的菊花吗?
再战能力
7.在第2题中,如果,求△BEF的周长。
23.1图形的旋转3
温故知新
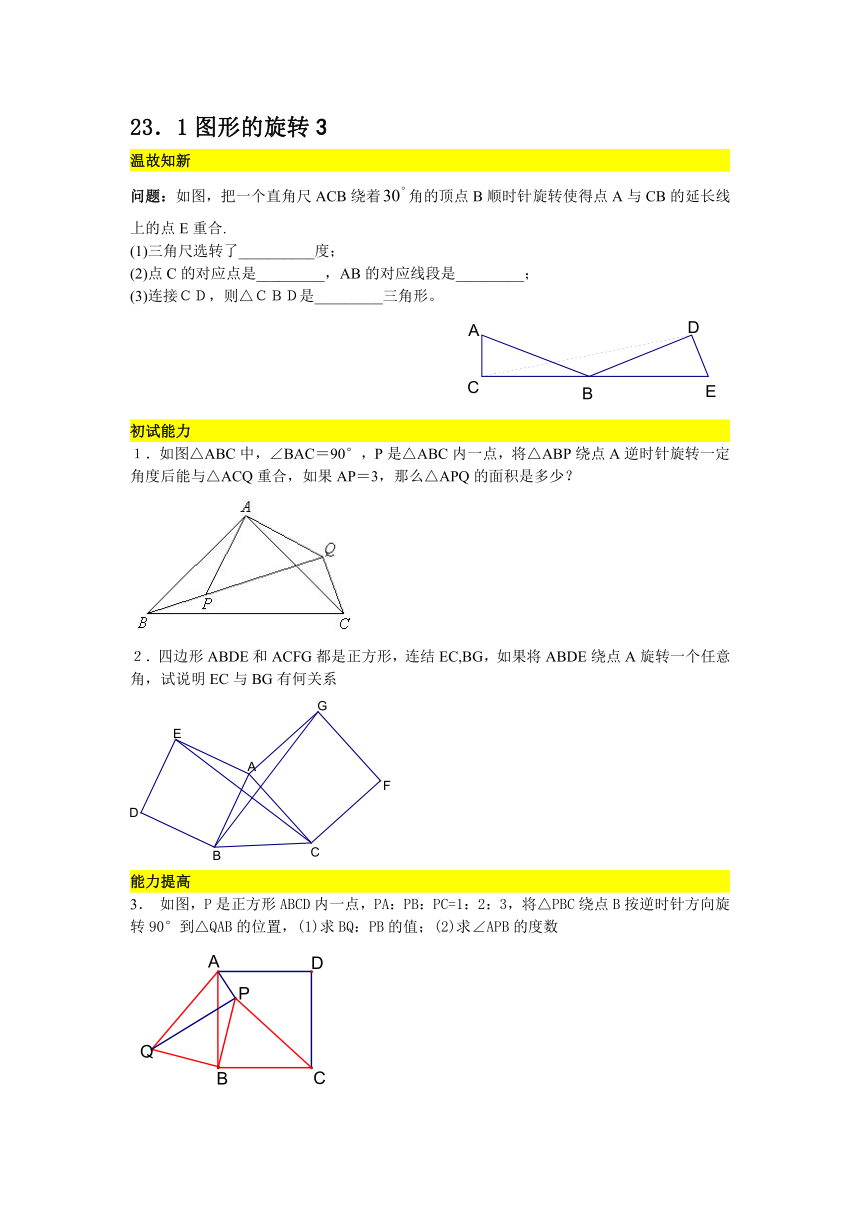
问题:如图,把一个直角尺ACB绕着角的顶点B顺时针旋转使得点A与CB的延长线上的点E重合.
(1)三角尺选转了__________度;
(2)点C的对应点是_________,AB的对应线段是_________;
(3)连接CD,则△CBD是_________三角形。
初试能力
1.如图△ABC中,∠BAC=90°,P是△ABC内一点,将△ABP绕点A逆时针旋转一定角度后能与△ACQ重合,如果AP=3,那么△APQ的面积是多少?
2.四边形ABDE和ACFG都是正方形,连结EC,BG,如果将ABDE绕点A旋转一个任意角,试说明EC与BG有何关系
能力提高
3. 如图,P是正方形ABCD内一点,PA:PB:PC=1:2:3,将△PBC绕点B按逆时针方向旋转90°到△QAB的位置,(1)求BQ:PB的值;(2)求∠APB的度数
综合应用
4.如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE.
(1)线段AF和BE有怎样的大小关系 请证明你的结论;
(2)将图a中的△CEF绕点C旋转一定的角度,得到图b,(1)中的结论还成立吗 作出判断并
说明理由;
再战能力
5. 已知:如图,E是正方形ABCD的边BC上一点,AF平分∠EAD交CD于点F,说明AE=BE+DF的理由。
23.1图形的旋转4
1.如图,P是正方形ABCD内一点,PA=1,PB=2,PC=3,求∠APB的度数
2.已知∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.
证明:PC=PD
3. (2006黑龙江)已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.
当三角板绕点C旋转到CD与OA垂直时(如图1),易证:OD+OE=OC.
当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立 若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系 请写出你的猜想,不需证明.
( http: / / www. )
图1 图2 图3
4.已知:如图,△ABC是等边三角形,∠ BDC=120°,求证:AD=BD+CD.
5.如图,将边长为的两个相互重合的正方形按住其中一个不动,另一个绕点B顺时针旋转一个角度,若重叠部分的面积是,求这个旋转角的度数。
6.如图,是一块直角三角形的土地,现在要在这块土地上挖一个正方形的鱼塘。已知剩余两直角三角形两条斜边长分别为和,问剩余两直角三角形土地面积和是多少?
23.2.1中心对称
初试能力
1.以点O为对称中心,作出点A的对称点A′;
2.以点O为对称中心,作出线段AB的对称线段点A′B′;
3. 如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′;
能力提高
4.画一个与已知四边形ABCD中心对称图形
(1)以顶点A为对称中心;
(2)以CD边的中点为对称中心。
5. 如图,已知等边三角形ABC和点O,画△A’B’C’,使△A’B’C’和△ABC关于点O
成中心对称。
6.如图,已知平行四边形ABCD和点O,请画出关于点O和平行四边形ABCD成中心对称的平行四边形。
综合应用
7.如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
再战能力
8. 如图,D为中BC边上的中点,M是AB边上的一点,N是AC边上的一点,且,求证:。
23.2.2中心对称图形
初试能力
1.选择题:
⑴下列图形中即是轴对称图形又是中心对称图形的是( )
A 角 B 等边三角形 C 线段 D平行四边形
(2) 下列多边形中,是中心对称图形而不是轴对称图形的是( )
A平行四边形 B矩形 C菱形 D正方形
(3)已知:下列命题中真命题的个数是( )
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A 0 B 1 C 2 D 3
(4)在一次游戏当中,小明将下面左图的四张扑克牌中的一张旋转180°后,得到右图,小亮看完,很快知道小明旋转了哪一张扑克,你知道为什么吗?
→
能力提高
2.如图一个方形内有一个任意一圆,请用一条直线同时将圆和长方形的面积平分?
3.一块如图所示的木板,如何用一条直线将其分为面积相等的两部分?
综合应用
4.已知:如图ABCD和矩形AB’C’D’关于A点对称,求证:四边形BDB’D’是菱形
5. 已知:如图AD是△ABC中∠A的平分线,DE//AC交AB于E.DF//AB交AC于F
求证:点E,F关于直线AD对称
再战能力
6. 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长.
23.2.3关于原点对称的点的坐标
新知探索
如图,在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、
E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答:
这些坐标与已知点的坐标有什么关系?
结论:即点P(x,y)关于原点O的对称点P′( )。
初试能力
1.如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
2.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出
△ABC关于原点对称的图形。
能力提高
3.四边形ABCD各顶点坐标分别为(5,0), (-2,3),(-1,0) , (-1,5), 作出与四边形ABCD关于原点O对称的图形.
4.平行四边形,A(1,2), B(-4,2), C(-2,-5),求出第四个点D的坐标. 若平行四边形在坐标系内关于原点对称,已知点A、点B的坐标不变,点C,点D的坐标又是什么
综合应用
5.下列函数的图象,一定关于原点成中心对称图形的是( )
A. y=1/x B. y=2x C. y=2x+1 D.以上三种都有可能.
6.如果点M(1-x,1-y)在第四象限,那么点N(1-x,y-1)关于原点对称点P在哪个象限?
再战能力
7. 如图,在平面直角坐标系中A.B坐标分别为(2,0),(-1,3),若△OAC与△OAB全等,(1)试尽可能多的写出点C的坐标;(2)在(1)的结果中请找出与(1,0)成中心对称的两个点。
7.如图,如图正方形EFOG的边长为5cm,绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积。
初试能力
1.如图:ABC是等边三角形,D是BC上一点, ABD经过旋转后到达ACE的位置
(1)旋转中心是________,点A的对应点是_____,点B的对应点是_____,点D的对应点是_____;
(2)旋转了多少度?请标出一个旋转角;
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
第1题图 第2题图
2.如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置
(1)旋转中心是________,点A的对应点是_____,点B的对应点是_____,点D的对应点是_____;
(2)△ADP是___________三角形。
3.如图:P是等边ABC内的一点,把ABP按不同的方向通过旋转得到BQC和ACR,请问:
(1)怎样旋转ABP至BQC的位置?
旋转中心_________,旋转方向_________,旋转角度__________;
(2)怎样旋转ABP至ACR的位置?
旋转中心_________,旋转方向_________,旋转角度__________;
(3)ACR是否可以直接通过把BQC旋转得到?
第3题图 第4题图
能力提高
4.如图,如果正方形DCEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个,分别是_____________________________________________。
5.如图,经过旋转后至的位置,
(1)旋转中心是__________;
(2)点A的对应点是_____,点B的对应点是_____,点D的对应点是_____;
(3)旋转角是多少度?
第5题图 第6题图
6.如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形?能否看作是某个图形关于O点旋转若干次形成的图形?
综合应用
7.如图,将绕点按顺时针方向旋转到的位置,已知斜边,,
(1)旋转中心是哪一点?
(2)如果连接,那么是怎样的三角形?
(3)点的旋转路径是多长?
再战能力
8.在上面问题中,设的中点是,连接,求的长度。
23.1图形的旋转2
初试能力
1.如图,ABC是等边三角形,D是BC上一点, 请画出ABD绕点A逆时针旋转后的三角形。
2.如图,正方形ABCD中,E、F分别是边AB、BC上的点,请画出DCF绕点D顺时针旋转后的三角形。
能力提高
3.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定旋转后的三角形.
4. 画出以下图所示的四边形ABCD以O点为中心,旋转角分别为30°、60°的旋转图形.
5.如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.
综合应用
5.如下图是菊花一叶和中心与圆圈,现以O为旋转中心画出分别旋转45°、90°、135°、180°、225°、270°、315°的菊花图案.
6. 如图,如果上面的菊花一叶,绕下面的点O′为旋转中心,请同学画出图案,它还是原来的菊花吗?
再战能力
7.在第2题中,如果,求△BEF的周长。
23.1图形的旋转3
温故知新
问题:如图,把一个直角尺ACB绕着角的顶点B顺时针旋转使得点A与CB的延长线上的点E重合.
(1)三角尺选转了__________度;
(2)点C的对应点是_________,AB的对应线段是_________;
(3)连接CD,则△CBD是_________三角形。
初试能力
1.如图△ABC中,∠BAC=90°,P是△ABC内一点,将△ABP绕点A逆时针旋转一定角度后能与△ACQ重合,如果AP=3,那么△APQ的面积是多少?
2.四边形ABDE和ACFG都是正方形,连结EC,BG,如果将ABDE绕点A旋转一个任意角,试说明EC与BG有何关系
能力提高
3. 如图,P是正方形ABCD内一点,PA:PB:PC=1:2:3,将△PBC绕点B按逆时针方向旋转90°到△QAB的位置,(1)求BQ:PB的值;(2)求∠APB的度数
综合应用
4.如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE.
(1)线段AF和BE有怎样的大小关系 请证明你的结论;
(2)将图a中的△CEF绕点C旋转一定的角度,得到图b,(1)中的结论还成立吗 作出判断并
说明理由;
再战能力
5. 已知:如图,E是正方形ABCD的边BC上一点,AF平分∠EAD交CD于点F,说明AE=BE+DF的理由。
23.1图形的旋转4
1.如图,P是正方形ABCD内一点,PA=1,PB=2,PC=3,求∠APB的度数
2.已知∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.
证明:PC=PD
3. (2006黑龙江)已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.
当三角板绕点C旋转到CD与OA垂直时(如图1),易证:OD+OE=OC.
当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立 若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系 请写出你的猜想,不需证明.
( http: / / www. )
图1 图2 图3
4.已知:如图,△ABC是等边三角形,∠ BDC=120°,求证:AD=BD+CD.
5.如图,将边长为的两个相互重合的正方形按住其中一个不动,另一个绕点B顺时针旋转一个角度,若重叠部分的面积是,求这个旋转角的度数。
6.如图,是一块直角三角形的土地,现在要在这块土地上挖一个正方形的鱼塘。已知剩余两直角三角形两条斜边长分别为和,问剩余两直角三角形土地面积和是多少?
23.2.1中心对称
初试能力
1.以点O为对称中心,作出点A的对称点A′;
2.以点O为对称中心,作出线段AB的对称线段点A′B′;
3. 如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′;
能力提高
4.画一个与已知四边形ABCD中心对称图形
(1)以顶点A为对称中心;
(2)以CD边的中点为对称中心。
5. 如图,已知等边三角形ABC和点O,画△A’B’C’,使△A’B’C’和△ABC关于点O
成中心对称。
6.如图,已知平行四边形ABCD和点O,请画出关于点O和平行四边形ABCD成中心对称的平行四边形。
综合应用
7.如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
再战能力
8. 如图,D为中BC边上的中点,M是AB边上的一点,N是AC边上的一点,且,求证:。
23.2.2中心对称图形
初试能力
1.选择题:
⑴下列图形中即是轴对称图形又是中心对称图形的是( )
A 角 B 等边三角形 C 线段 D平行四边形
(2) 下列多边形中,是中心对称图形而不是轴对称图形的是( )
A平行四边形 B矩形 C菱形 D正方形
(3)已知:下列命题中真命题的个数是( )
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A 0 B 1 C 2 D 3
(4)在一次游戏当中,小明将下面左图的四张扑克牌中的一张旋转180°后,得到右图,小亮看完,很快知道小明旋转了哪一张扑克,你知道为什么吗?
→
能力提高
2.如图一个方形内有一个任意一圆,请用一条直线同时将圆和长方形的面积平分?
3.一块如图所示的木板,如何用一条直线将其分为面积相等的两部分?
综合应用
4.已知:如图ABCD和矩形AB’C’D’关于A点对称,求证:四边形BDB’D’是菱形
5. 已知:如图AD是△ABC中∠A的平分线,DE//AC交AB于E.DF//AB交AC于F
求证:点E,F关于直线AD对称
再战能力
6. 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长.
23.2.3关于原点对称的点的坐标
新知探索
如图,在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、
E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答:
这些坐标与已知点的坐标有什么关系?
结论:即点P(x,y)关于原点O的对称点P′( )。
初试能力
1.如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
2.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出
△ABC关于原点对称的图形。
能力提高
3.四边形ABCD各顶点坐标分别为(5,0), (-2,3),(-1,0) , (-1,5), 作出与四边形ABCD关于原点O对称的图形.
4.平行四边形,A(1,2), B(-4,2), C(-2,-5),求出第四个点D的坐标. 若平行四边形在坐标系内关于原点对称,已知点A、点B的坐标不变,点C,点D的坐标又是什么
综合应用
5.下列函数的图象,一定关于原点成中心对称图形的是( )
A. y=1/x B. y=2x C. y=2x+1 D.以上三种都有可能.
6.如果点M(1-x,1-y)在第四象限,那么点N(1-x,y-1)关于原点对称点P在哪个象限?
再战能力
7. 如图,在平面直角坐标系中A.B坐标分别为(2,0),(-1,3),若△OAC与△OAB全等,(1)试尽可能多的写出点C的坐标;(2)在(1)的结果中请找出与(1,0)成中心对称的两个点。
7.如图,如图正方形EFOG的边长为5cm,绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积。
同课章节目录
