数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算课件(共36张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算课件(共36张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 00:00:00 | ||
图片预览








文档简介
(共36张PPT)
1.1.1空间向量及其线性运算
新知探究
2
新知引入
教学目标:
(1)经历向量及其运算由平面向空间推广的过程,了解空间向量的概念,发展
数学抽象素养;
(2)掌握空间向量的加法、减法、数乘运算及其表示;
(3)掌握空间向量加法、减法、数乘的运算律;
(4)借助向量的线性运算的学习,提升数学运算素养.
教学重点:空间向量的概念和线性运算及其应用
教学难点:空间向量的线性运算及其应用
1、定义:
平面内既有大小又有方向的量。
几何表示法:用有向线段表示
字母表示法:
用小写字母表示,或者用表示向量的
有向线段的起点和终点字母表示。
相等向量:长度相等且方向相同的向量
A
B
C
D
2、表示法:
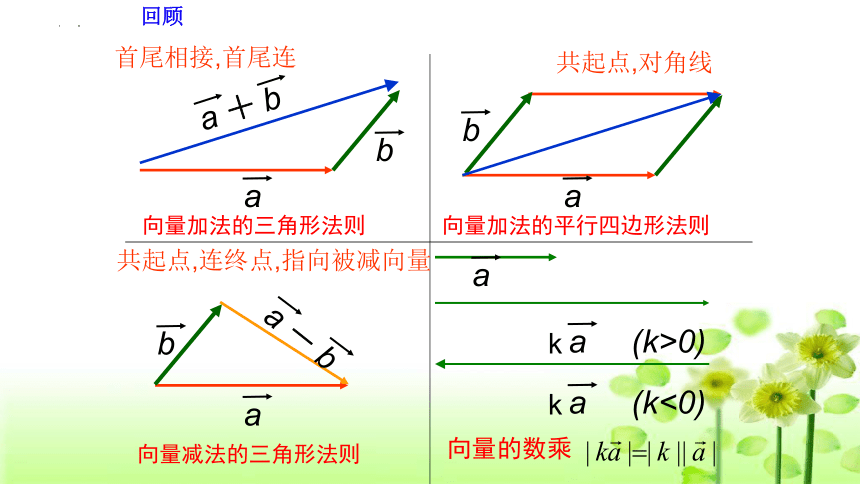
回顾
向量加法的三角形法则
a
b
向量加法的平行四边形法则
b
a
向量减法的三角形法则
a
b
a -
b
a +
b
a (k>0)
k
a (k<0)
k
向量的数乘
a
首尾相接,首尾连
共起点,对角线
共起点,连终点,指向被减向量
回顾
加法交换律:
加法结合律:
数乘分配律:
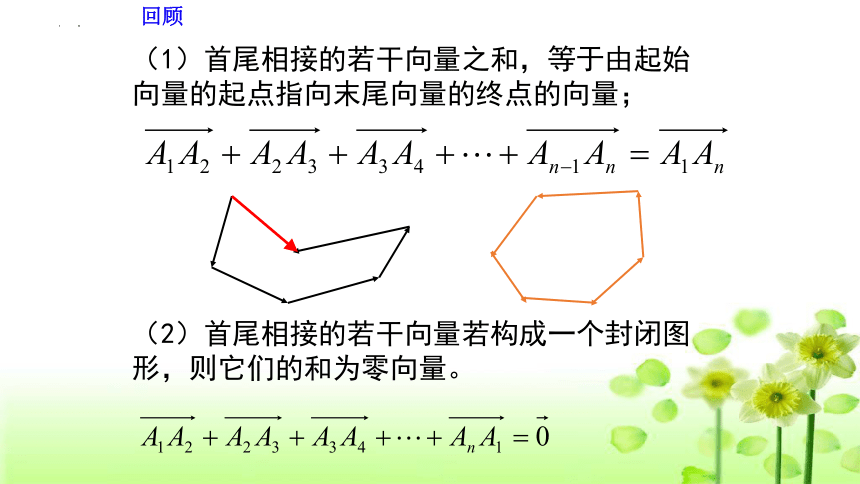
回顾
(1)首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;
(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为零向量。
回顾
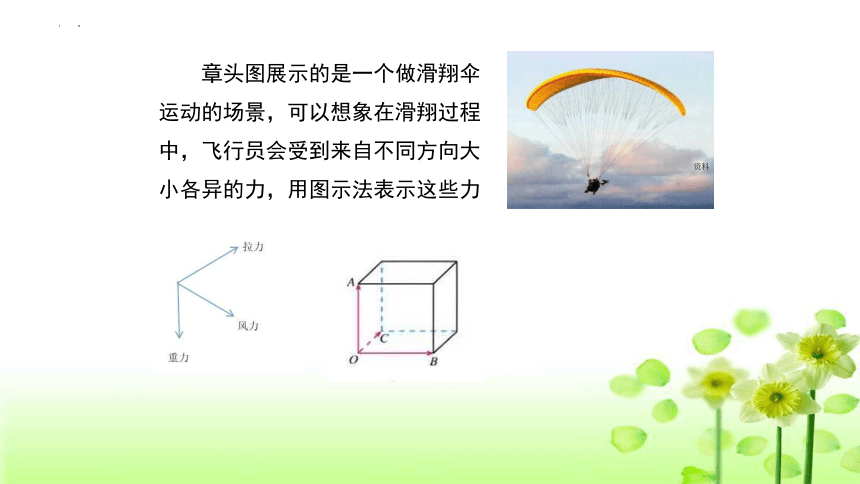
章头图展示的是一个做滑翔伞运动的场景,可以想象在滑翔过程中,飞行员会受到来自不同方向大小各异的力,用图示法表示这些力
资料
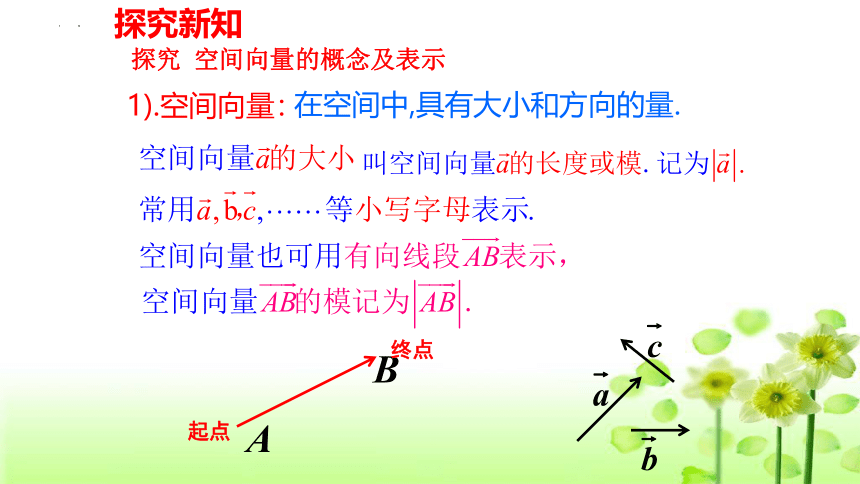
起点
终点
探究新知
在空间中,具有大小和方向的量.
1).空间向量:
探究 空间向量的概念及表示
2)零向量
3)单位向量
当有向线段的起点A与终点B重合时,
4)相反向量
5)相等向量
思考1:空间中任意两个向量共面吗?
共面
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
6)共线向量(平行向量)
问题 平面向量与空间向量有什么区别与联系?
(1)区别:平面向量研究的是二维平面的向量,空间向量研究的是三维空间的向量.
(2)联系:空间向量的定义、表示方法及零向量、单位向量、相反向量、相等向量和共线向量(平行向量)的概念都与平面向量相同.
问题探究
数学中,引进一种量后,一个很自然的问题就是要研究它们的运算. 那么在学习了空间向量的概念之后,空间向量如何进行线性运算呢?
复习回顾·平面向量的线性运算
(1)加减运算
三角形法则:
首尾相连
平行四边形法则:
共起点
减法法则:
共起点,
连终点,
指被减
复习回顾·平面向量的线性运算
(2)数乘运算
实数λ与平面向量a的积是一个向量,记作λa,其长度和方向规定如下:
① |λa|=|λ||a|;
②若λ > 0,λa与a的方向相同;
若λ < 0,λa与a的方向相反;
若λ=0,λa=0.
O
A
Q
P
M
N
a
λa
(λ>0)
λa
(λ<0)
问题探究
如何进行空间向量的线性运算?
a
b
.
O
α
转化
平面向量的线性运算
空间向量的线性运算
空间向量的线性运算
(1)加减运算:
(2)数乘运算:
三角形法则、平行四边形法则
实数λ与空间向量a的积是一个向量,记作λa,其长度和方向规定如下:
① |λa|=|λ||a|;
②若λ > 0,λa与a的方向相同;
若λ < 0,λa与a的方向相反;
若λ=0,λa=0.
空间向量线性运算的运算律
①交换律: a + b=b + a;
②结合律: a + (b + c)
=(a + b) + c,
λ(μa)=(λμ)a;
③分配律: (λ+μ)a=λa + μa,
λ(a+b)=λa + λb.
问题 如图1.1-6,在平行六面体 中,分别标出 , 表示的向量.从中体会向量加法运算的交换律和结合律.一般地,三个不共面的向量的和与这三个向量有什么关系?
探究 共线向量及方向向量
问题 对任意两个空间向量 a 与 b,如果 ,a与 b有什么位置关系?反过来,a 与 b 有什么位置关系时,?
类似于平面向量共线的充要条件,对任意两个空间向量 a,b
,的充要条件是存在实数 λ ,使 .(共线向量定理)
如图1.1-7,O 是直线 l 上一点,在直线l上取非零向量 a ,则对于直线 l 上任意一点 P ,由数乘向量的定义及向量共线的充要条件可知,存在实数 λ ,使得 .
与向量 a 平行的非零向量称为直线 l 的方向向量.
方向向量
这样,直线 l 上任意一点都可以由直线l上的一点和它的方向向量表示。
思考:给定一点和一个方向向量可以确定一条直线吗?
如图,如果表示向量a的有向线段 所在的直线OA与直线l平行或重合,那么称向量a平行于直线l.
如果直线OA平行于平面α或在平面α内,那么称向量a平行于平面α.平行于同一平面的向量,叫做共面向量.
探究新知
α
a
a
l
a
O
A
思考:我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的.那么,什么情况下三个空间向量共面呢?
探究新知
探究:对平面内任意两个不共线向量a,b,由平面向量基本定理可知,这个平面内的任意一个向量p可以写成p=xa+yb,其中(x, y)是唯一确定的有序实数对.对两个不共线的空间向量a,b,如果p=xa+yb,那么向量p与向量a,b有什么位置关系 反过来,向量p与向量a,b有什么位置关系时,p=xa+yb
发现:
如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x, y),使p=xa+yb.
类型向量共面问题例 如图,已知平行四边形ABCD,从平
面AC外一点O引向量 , ,
, ,
求证:
⑴四点E、F、G、H共面;
⑵平面EG//平面AC.
例题讲评
证明:
∵四边形ABCD为
①
∴
(﹡)
(﹡)代入
所以 E、F、G、H共面。
例: 已知 ABCD ,从平面AC外一点O引向量
求证:①四点E、F、G、H共面;
②平面AC//平面EG。
证明:
由面面平行判定定理的推论得:
②
由①知
A
B
C
D
A1
B1
C1
D1
例:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。
例题讲评
A
B
C
D
A1
B1
C1
D1
例:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。
A
B
C
D
A1
B1
C1
D1
例题讲评
A
B
C
D
A1
B1
C1
D1
例:已知平行六面体ABCD-A1B1C1D1,求满足下列各式的x的值。
例题讲评
A
B
C
D
A1
B1
C1
D1
例:已知平行六面体ABCD-A1B1C1D1,求满足下列各式的x的值。
例题讲评
1.如图,E,F分别是长方体ABCD-A'B'C'D'的棱AB,CD的中点,化简下列表达式,并在图中标出化简结果的向量:
(1) ; (2) ;
(3) ; (4) .
巩固练习
A
B
D
C
A'
B'
D'
C'
E
F
解:(1)
(2)
(3)
(4)
2.如图平行六面体ABCD-A'B'C'D',用 表示 及 .
巩固练习
A
B
C'
B'
A'
D
C
D'
解:
3.如图,已知正方体ABCD-A'B'C'D',E,F分别是上底面A'C'和侧面CD'的中心,求下列各式中x, y的值:
巩固练习
B
C
A
D
B'
C'
A'
D'
E
F
(2)
(1)
(3)
解:(1)
(2)
(3)
课堂小结
1.知识清单:
(1)向量的概念.(2)向量的线性运算(加法、减法和数乘).(3)向量的线性运算的运算律.
(4)空间向量共线的充要条件,直线的方向向量.(5)空间向量共面的充要条件.
2.方法归纳:
三角形法则、平行四边形法则、数形结合思想、转化化归思想.
3.常见误区:
(1)对空间向量的理解应抓住向量的“大小”和“方向”两个要素,并注意它是一个“量”,而不是一个数.
(2)混淆向量共线与线段共线、点共线.
谢 谢!
1.1.1空间向量及其线性运算
新知探究
2
新知引入
教学目标:
(1)经历向量及其运算由平面向空间推广的过程,了解空间向量的概念,发展
数学抽象素养;
(2)掌握空间向量的加法、减法、数乘运算及其表示;
(3)掌握空间向量加法、减法、数乘的运算律;
(4)借助向量的线性运算的学习,提升数学运算素养.
教学重点:空间向量的概念和线性运算及其应用
教学难点:空间向量的线性运算及其应用
1、定义:
平面内既有大小又有方向的量。
几何表示法:用有向线段表示
字母表示法:
用小写字母表示,或者用表示向量的
有向线段的起点和终点字母表示。
相等向量:长度相等且方向相同的向量
A
B
C
D
2、表示法:
回顾
向量加法的三角形法则
a
b
向量加法的平行四边形法则
b
a
向量减法的三角形法则
a
b
a -
b
a +
b
a (k>0)
k
a (k<0)
k
向量的数乘
a
首尾相接,首尾连
共起点,对角线
共起点,连终点,指向被减向量
回顾
加法交换律:
加法结合律:
数乘分配律:
回顾
(1)首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;
(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为零向量。
回顾
章头图展示的是一个做滑翔伞运动的场景,可以想象在滑翔过程中,飞行员会受到来自不同方向大小各异的力,用图示法表示这些力
资料
起点
终点
探究新知
在空间中,具有大小和方向的量.
1).空间向量:
探究 空间向量的概念及表示
2)零向量
3)单位向量
当有向线段的起点A与终点B重合时,
4)相反向量
5)相等向量
思考1:空间中任意两个向量共面吗?
共面
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
6)共线向量(平行向量)
问题 平面向量与空间向量有什么区别与联系?
(1)区别:平面向量研究的是二维平面的向量,空间向量研究的是三维空间的向量.
(2)联系:空间向量的定义、表示方法及零向量、单位向量、相反向量、相等向量和共线向量(平行向量)的概念都与平面向量相同.
问题探究
数学中,引进一种量后,一个很自然的问题就是要研究它们的运算. 那么在学习了空间向量的概念之后,空间向量如何进行线性运算呢?
复习回顾·平面向量的线性运算
(1)加减运算
三角形法则:
首尾相连
平行四边形法则:
共起点
减法法则:
共起点,
连终点,
指被减
复习回顾·平面向量的线性运算
(2)数乘运算
实数λ与平面向量a的积是一个向量,记作λa,其长度和方向规定如下:
① |λa|=|λ||a|;
②若λ > 0,λa与a的方向相同;
若λ < 0,λa与a的方向相反;
若λ=0,λa=0.
O
A
Q
P
M
N
a
λa
(λ>0)
λa
(λ<0)
问题探究
如何进行空间向量的线性运算?
a
b
.
O
α
转化
平面向量的线性运算
空间向量的线性运算
空间向量的线性运算
(1)加减运算:
(2)数乘运算:
三角形法则、平行四边形法则
实数λ与空间向量a的积是一个向量,记作λa,其长度和方向规定如下:
① |λa|=|λ||a|;
②若λ > 0,λa与a的方向相同;
若λ < 0,λa与a的方向相反;
若λ=0,λa=0.
空间向量线性运算的运算律
①交换律: a + b=b + a;
②结合律: a + (b + c)
=(a + b) + c,
λ(μa)=(λμ)a;
③分配律: (λ+μ)a=λa + μa,
λ(a+b)=λa + λb.
问题 如图1.1-6,在平行六面体 中,分别标出 , 表示的向量.从中体会向量加法运算的交换律和结合律.一般地,三个不共面的向量的和与这三个向量有什么关系?
探究 共线向量及方向向量
问题 对任意两个空间向量 a 与 b,如果 ,a与 b有什么位置关系?反过来,a 与 b 有什么位置关系时,?
类似于平面向量共线的充要条件,对任意两个空间向量 a,b
,的充要条件是存在实数 λ ,使 .(共线向量定理)
如图1.1-7,O 是直线 l 上一点,在直线l上取非零向量 a ,则对于直线 l 上任意一点 P ,由数乘向量的定义及向量共线的充要条件可知,存在实数 λ ,使得 .
与向量 a 平行的非零向量称为直线 l 的方向向量.
方向向量
这样,直线 l 上任意一点都可以由直线l上的一点和它的方向向量表示。
思考:给定一点和一个方向向量可以确定一条直线吗?
如图,如果表示向量a的有向线段 所在的直线OA与直线l平行或重合,那么称向量a平行于直线l.
如果直线OA平行于平面α或在平面α内,那么称向量a平行于平面α.平行于同一平面的向量,叫做共面向量.
探究新知
α
a
a
l
a
O
A
思考:我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的.那么,什么情况下三个空间向量共面呢?
探究新知
探究:对平面内任意两个不共线向量a,b,由平面向量基本定理可知,这个平面内的任意一个向量p可以写成p=xa+yb,其中(x, y)是唯一确定的有序实数对.对两个不共线的空间向量a,b,如果p=xa+yb,那么向量p与向量a,b有什么位置关系 反过来,向量p与向量a,b有什么位置关系时,p=xa+yb
发现:
如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x, y),使p=xa+yb.
类型向量共面问题例 如图,已知平行四边形ABCD,从平
面AC外一点O引向量 , ,
, ,
求证:
⑴四点E、F、G、H共面;
⑵平面EG//平面AC.
例题讲评
证明:
∵四边形ABCD为
①
∴
(﹡)
(﹡)代入
所以 E、F、G、H共面。
例: 已知 ABCD ,从平面AC外一点O引向量
求证:①四点E、F、G、H共面;
②平面AC//平面EG。
证明:
由面面平行判定定理的推论得:
②
由①知
A
B
C
D
A1
B1
C1
D1
例:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。
例题讲评
A
B
C
D
A1
B1
C1
D1
例:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。
A
B
C
D
A1
B1
C1
D1
例题讲评
A
B
C
D
A1
B1
C1
D1
例:已知平行六面体ABCD-A1B1C1D1,求满足下列各式的x的值。
例题讲评
A
B
C
D
A1
B1
C1
D1
例:已知平行六面体ABCD-A1B1C1D1,求满足下列各式的x的值。
例题讲评
1.如图,E,F分别是长方体ABCD-A'B'C'D'的棱AB,CD的中点,化简下列表达式,并在图中标出化简结果的向量:
(1) ; (2) ;
(3) ; (4) .
巩固练习
A
B
D
C
A'
B'
D'
C'
E
F
解:(1)
(2)
(3)
(4)
2.如图平行六面体ABCD-A'B'C'D',用 表示 及 .
巩固练习
A
B
C'
B'
A'
D
C
D'
解:
3.如图,已知正方体ABCD-A'B'C'D',E,F分别是上底面A'C'和侧面CD'的中心,求下列各式中x, y的值:
巩固练习
B
C
A
D
B'
C'
A'
D'
E
F
(2)
(1)
(3)
解:(1)
(2)
(3)
课堂小结
1.知识清单:
(1)向量的概念.(2)向量的线性运算(加法、减法和数乘).(3)向量的线性运算的运算律.
(4)空间向量共线的充要条件,直线的方向向量.(5)空间向量共面的充要条件.
2.方法归纳:
三角形法则、平行四边形法则、数形结合思想、转化化归思想.
3.常见误区:
(1)对空间向量的理解应抓住向量的“大小”和“方向”两个要素,并注意它是一个“量”,而不是一个数.
(2)混淆向量共线与线段共线、点共线.
谢 谢!
