等腰梯形性质定理和判定定理及其证明

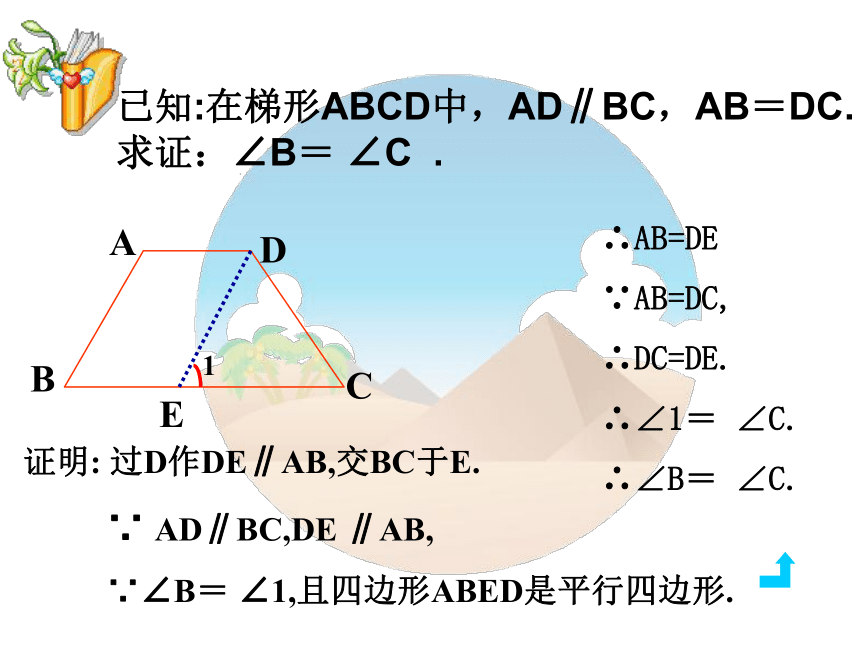
课件15张PPT。大家好！性质定理和判定定理及其证明等腰梯形温故知新:1.什么是梯形?2.什么是等腰梯形?一组对边平行而另一组对边不平行的四边形叫做梯形.两腰相等的梯形叫做等腰梯形.等腰梯形在同一底上的两个角相等.等腰梯形的对角线相等.等腰梯形的性质:已知:在梯形ABCD中，AD∥BC，AB＝DC.
求证：∠B＝ ∠C .E
∴AB=DE
∵AB=DC,
∴DC=DE.
∴∠1＝ ∠C.
∴∠B＝ ∠C.

证明: 过D作DE∥AB,交BC于E.
∵ AD∥BC,DE ∥AB,
∵∠B＝ ∠1,且四边形ABED是平行四边形.
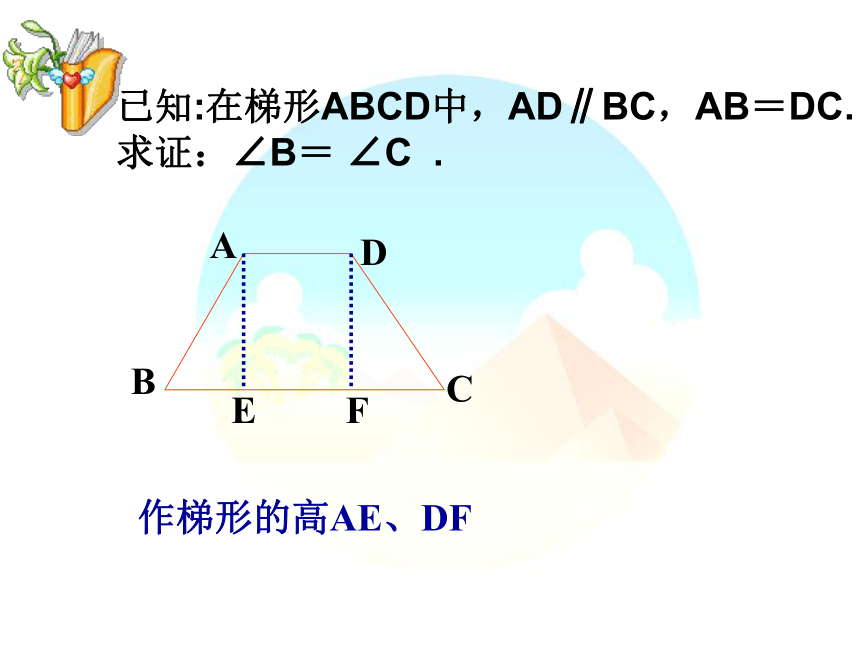
1已知:在梯形ABCD中，AD∥BC，AB＝DC.
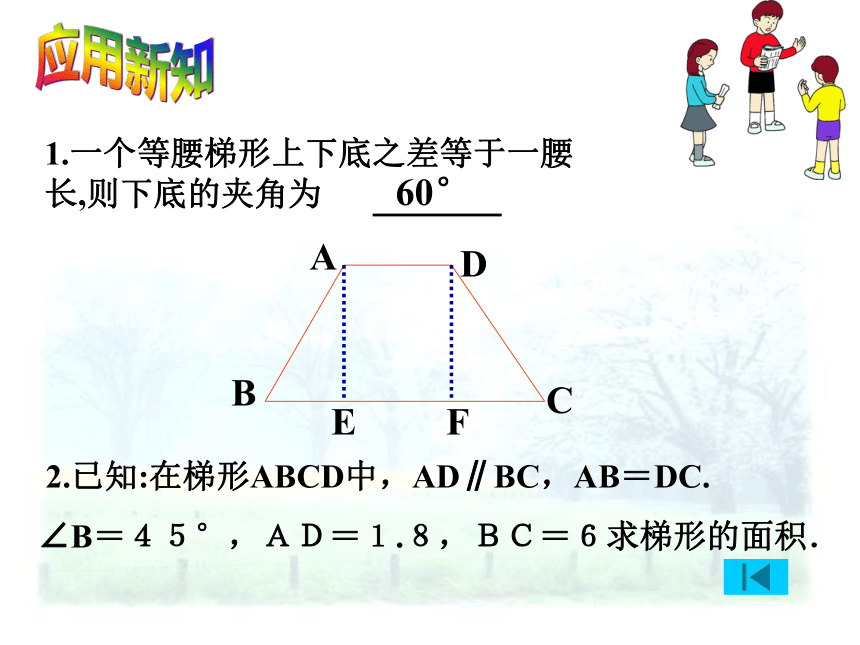
求证：∠B＝ ∠C .EF作梯形的高AE、DF应用新知1.一个等腰梯形上下底之差等于一腰长,则下底的夹角为 2.已知:在梯形ABCD中，AD∥BC，AB＝DC.
∠B＝４５°，ＡＤ＝１.８，ＢＣ＝６求梯形的面积．EF60°已知：在梯形ABCD中，AD∥BC， AB=DC.
求证： AC＝BD.等腰梯形的判定:在同一底上的两个角相等的梯形是等 腰梯形
对角线相等的梯形是等腰梯形已知:在梯形ABCD中，AD∥BC， ∠B＝ ∠C.
求证：AB＝DC.1EF过D作DE∥AB,交BC于E.作梯形的高AE、DFE已知:在梯形ABCD中，AD∥BC， ∠B＝ ∠C.
求证：AB＝DC.分别延长BA、CD,它们相交于点EE12已知：在梯形ABCD中，AD∥BC， AC＝BD.
求证： AB=DC.想一想E12过点D作DE ∥AC， 交BC的延长线于E巩固练习:1.下列命题中正确的是( )
A.对角线相等的四边形是矩形或等腰梯形.
B.一组对边平行,另一组对边相等的四边形是等腰梯形.
C.两组对角分别互补的四边形是等腰梯形.
D.等腰梯形是轴对称图形,经过两底中点的直线是它的对称轴.2.已知：在梯形ABCD中，AD∥BC，AB=DC,对角线AC、BD相交于点O.
求证： OB=OC.O提示：证△ABC≌△DCB（SAS）
∴∠OCB＝∠OBC
∴在△BOC中，OB=OC
12D小结：本节课你学会了哪些知识和技巧技能？1、梯形中常用的四种辅助线的添法2、等腰梯形的判定步骤：
（1）判梯形
（2）两腰或两角或对角线相等
再见！