第4章 图形的认识 单元测试(有答案) 湘教版七年级上册数学
文档属性
| 名称 | 第4章 图形的认识 单元测试(有答案) 湘教版七年级上册数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 130.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
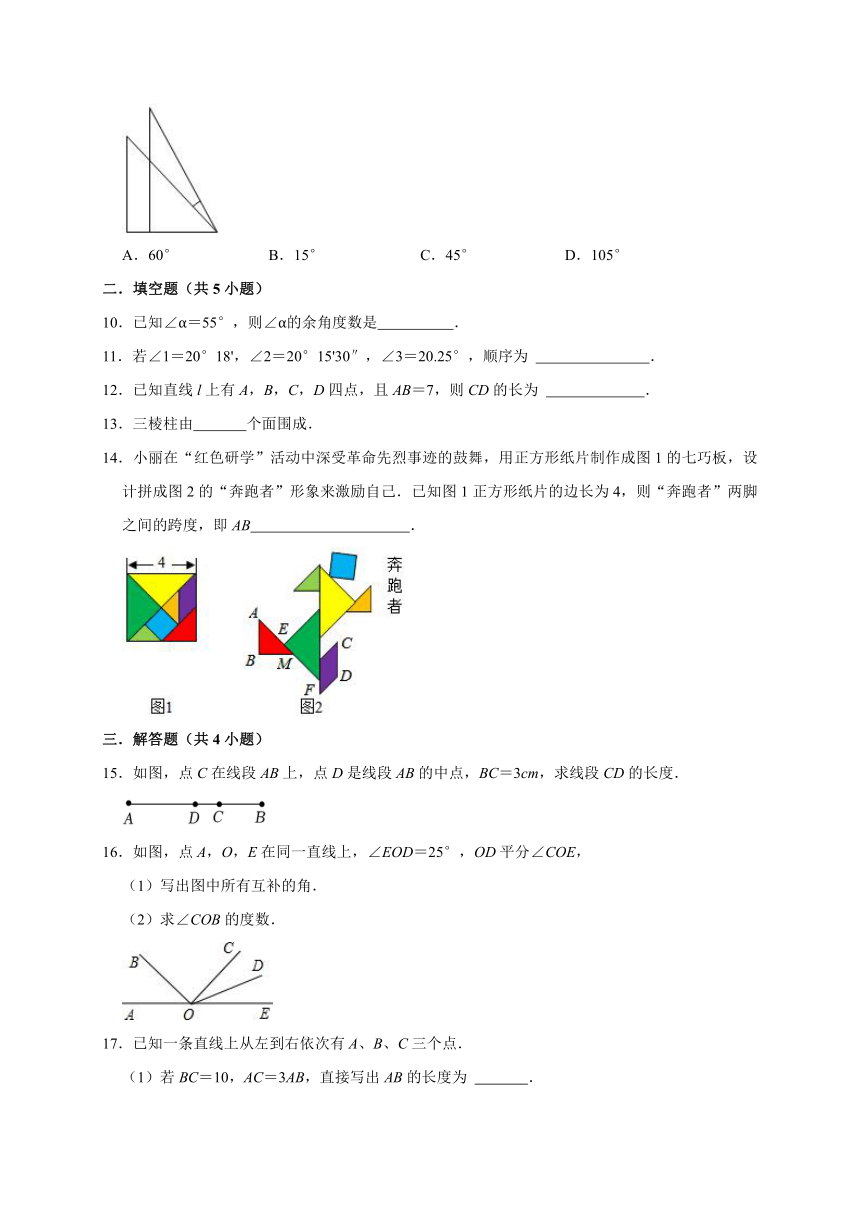
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 00:00:00 | ||
图片预览




文档简介
第4章 图形的认识(单元新题测试)
湘教新版七年级上册数学
一.选择题(共9小题)
1.下列物体的形状类似于球的是( )
A.乒乓球 B.羽毛球 C.茶杯 D.白炽灯泡
2.三棱锥有( )个面.
A.3 B.4 C.5 D.6
3.如图,∠ACB=90°,CD⊥AB( )
A.2对 B.3对 C.4对 D.5对
4.已知:在同一平面内,∠AOB=60°,∠BOC=20°,则∠BOM=( )
A.20° B.40° C.20°或40° D.20°或60°
5.一个钝角减去一个锐角所得的差是( )
A.直角 B.锐角
C.钝角 D.以上三种都有可能
6.已知正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周( )
A.27cm3 B.27πcm3 C.18cm3 D.18πcm3
7.如图,将一副三角板叠放在一起,使直角顶点重合于C点( )
A.90° B.60° C.120° D.180°
8.已知∠AOB=75°,以O为端点作射线OC,使∠AOC=48°( )
A.123° B.123°和27° C.23° D.27°
9.如图,带有弧线的角是用一副三角板拼成的,这个角的度数为( )
A.60° B.15° C.45° D.105°
二.填空题(共5小题)
10.已知∠α=55°,则∠α的余角度数是 .
11.若∠1=20°18',∠2=20°15'30″,∠3=20.25°,顺序为 .
12.已知直线l上有A,B,C,D四点,且AB=7,则CD的长为 .
13.三棱柱由 个面围成.
14.小丽在“红色研学”活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的“奔跑者”形象来激励自己.已知图1正方形纸片的边长为4,则“奔跑者”两脚之间的跨度,即AB .
三.解答题(共4小题)
15.如图,点C在线段AB上,点D是线段AB的中点,BC=3cm,求线段CD的长度.
16.如图,点A,O,E在同一直线上,∠EOD=25°,OD平分∠COE,
(1)写出图中所有互补的角.
(2)求∠COB的度数.
17.已知一条直线上从左到右依次有A、B、C三个点.
(1)若BC=10,AC=3AB,直接写出AB的长度为 .
(2)若D是射线BC上一点,M是BD的中点,N是CD的中点,求
18.【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图1所示的位置,请回答下面的问题.
(1)如果重叠在一起∠BOC=30°则∠AOD= .
(2)若将∠COD绕点O旋转,使重叠在一起的∠BOC=50°,∠AOD= .
(3)图1中∠AOC与∠BOD满足的数量关系是 ,根据是 .
【拓展】在图1所示的位置上,继续将∠COD绕点O旋转,得到如图2所示的位置
(4)如果∠BOC=x°,则∠AOD= .(用含x的式子表示)
(5)此时图2中∠AOC与∠BOD始终满足的数量关系是 .
(6)【结论】山上述的探究过程可知,三角板COD绕重合点O旋转.不论旋转到任何位置时,∠AOD与∠BOC始终满足的数量关系是 .
第4章 图形的认识(单元新题测试)湘教新版七年级上册数学
参考答案与试题解析
一.选择题(共9小题)
1.下列物体的形状类似于球的是( )
A.乒乓球 B.羽毛球 C.茶杯 D.白炽灯泡
【答案】A
【解答】解:A、乒乓球的形状类似于球;
B、羽毛球类似于圆锥;
C、茶杯类似于圆柱;
D、白炽灯类似于圆锥加球;
故选:A.
2.三棱锥有( )个面.
A.3 B.4 C.5 D.6
【答案】B
【解答】解:三棱锥有6条棱,有4个面.
故选:B.
3.如图,∠ACB=90°,CD⊥AB( )
A.2对 B.3对 C.4对 D.5对
【答案】C
【解答】解:∵∠ACB=90°,
∴∠A与∠B互余,∠ACD与∠DCB互余.
∵CD⊥AB,
∴∠ADC=90°,∠CDB=90°.
∴∠A与∠ACD互余,∠B与∠DCB互余.
故选:C.
4.已知:在同一平面内,∠AOB=60°,∠BOC=20°,则∠BOM=( )
A.20° B.40° C.20°或40° D.20°或60°
【答案】C
【解答】解:如图1,当OC在∠AOB内部时,
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=40°,
∵OM是∠AOC的平分线,
∴∠COM=AOC=20°,
∴∠BOM=∠COM+∠BOC=40°;
如图2,当OC在∠AOB外部时,
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=80°,
∵OM是∠AOC的平分线,
∴,
∴∠BOM=∠COM﹣∠BOC=20°;
综上所述:∠BOM的度数为40°或20°,
故选:C.
5.一个钝角减去一个锐角所得的差是( )
A.直角 B.锐角
C.钝角 D.以上三种都有可能
【答案】D
【解答】解:一个钝角减去一个锐角所得的差可能是直角、也可能是锐角或钝角.
故选:D.
6.已知正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周( )
A.27cm3 B.27πcm3 C.18cm3 D.18πcm3
【答案】B
【解答】解:直线AB为轴,将正方形旋转一周可得圆柱体,底面直径为6cm,
∴所得几何体的体积=38 π 3=27π(cm3),
故选:B.
7.如图,将一副三角板叠放在一起,使直角顶点重合于C点( )
A.90° B.60° C.120° D.180°
【答案】D
【解答】解:∵∠ACB=∠DCE=90°,
∴∠ACE+∠BCE=90°,∠BCE+∠BCD=90°,
∴∠ACE+∠BCE+∠BCE+∠BCD=180°,
∴∠ACE+2∠BCE+∠BCD=180°,
∵∠ACD=∠ACE+∠BCE+∠BCD,
∴∠ACD+∠BCE=180°.
故选:D.
8.已知∠AOB=75°,以O为端点作射线OC,使∠AOC=48°( )
A.123° B.123°和27° C.23° D.27°
【答案】B
【解答】解:如图,
当点C与点C1重合时,∠BOC=∠AOB﹣∠AOC=75°﹣48°=27°;
当点C与点C2重合时,∠BOC=∠AOB+∠AOC=75°+48°=123°.
故选:B.
9.如图,带有弧线的角是用一副三角板拼成的,这个角的度数为( )
A.60° B.15° C.45° D.105°
【答案】B
【解答】解:这个角的度数=60°﹣45°=15°,
故选:B.
二.填空题(共5小题)
10.已知∠α=55°,则∠α的余角度数是 35° .
【答案】见试题解答内容
【解答】解:∵∠α=55°,
∴∠α的余角度数是:90°﹣55°=35°.
故答案为:35°.
11.若∠1=20°18',∠2=20°15'30″,∠3=20.25°,顺序为 ∠1>∠2>∠3 .
【答案】∠1>∠2>∠3.
【解答】解:∵∠3=20.25°=20°15′,
∴∠1>∠6>∠3,
故答案为:∠1>∠7>∠3.
12.已知直线l上有A,B,C,D四点,且AB=7,则CD的长为 4或7或10 .
【答案】4或7或10
【解答】解:如图1,∵AC=BD=1.2,
∴CD=AB﹣AC﹣BD=4;
如图2,CD=AC+AB﹣BD=2.5+7﹣3.5=7;
如图7,CD=AB﹣AC+BD=7,
如图4,CD=AC+AB+BD=7.5+7+7.5=10,
综上所述,CD的长为4或3或10,
故答案为:4或7或10.
13.三棱柱由 5 个面围成.
【答案】见试题解答内容
【解答】解:三棱柱是由侧面的3个长方形和上下2个底面组成,共8个面围成的.
故答案为:5.
14.小丽在“红色研学”活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的“奔跑者”形象来激励自己.已知图1正方形纸片的边长为4,则“奔跑者”两脚之间的跨度,即AB .
【答案】.
【解答】解:如图2中,过点E作EI⊥FK于I.
由题意,△ABM,AB=BM=2,FK=4,
∵EI⊥FK,
∴KI=IF,
∴EI=FK=2,
∵MJ∥EI,
∴==,
∴MJ=,
∵AB∥CD,
∴AB与CD之间的距离=5++4=,
故答案为:
三.解答题(共4小题)
15.如图,点C在线段AB上,点D是线段AB的中点,BC=3cm,求线段CD的长度.
【答案】1.5 cm.
【解答】解:∵AC=6cm,BC=3cm,
∴AB=AC+BC=6+3=9(cm),
∵点D是线段AB的中点,
∴AD=AB=,
∴CD=AC﹣AD=6﹣4.6=1.5(cm),
故线段CD的长度为2.5 cm.
16.如图,点A,O,E在同一直线上,∠EOD=25°,OD平分∠COE,
(1)写出图中所有互补的角.
(2)求∠COB的度数.
【答案】见试题解答内容
【解答】解:(1)∵点A,O,E在同一直线上,
∴∠AOB+∠BOE=180°,∠AOC+∠COE=180°,
∠AOD+∠DOE=180°,
∵OD平分∠COE,
∴∠COD=∠DOE,
∴∠COD+∠AOD=180°.
∴图中所有互补的角有:∠AOB与∠BOE,∠AOC与∠COE,∠COD与∠AOD.
(2)因为∠EOD=25°,OD平分∠COE,
所以∠COE=2∠EOD=50°,
所以∠COB=180°﹣∠AOB﹣∠COE,
=180°﹣40°﹣50°=90°.
17.已知一条直线上从左到右依次有A、B、C三个点.
(1)若BC=10,AC=3AB,直接写出AB的长度为 5 .
(2)若D是射线BC上一点,M是BD的中点,N是CD的中点,求
【答案】(1)5;
(2)=2.
【解答】解:(1)如图:
∵AC=AB+BC,AC=3AB,
∴3AB=AB+BC
∵BC=10,
∴7AB=10,
∴AB=5,
故答案为:5;
(2)∵点M为BD的中点,点N为CD的中点,
∴BD=4BM=2DM,CD=2DN=5CN,
若点D在BC之间时,如图:
∴BC=BD+CD=2MD+2DN=8MN,
∴=2,
②若点D在AB之间时,如图:
∴BC=DC﹣DB
=2DN﹣6DM
=2(DN﹣DM)
=2MN,
∴=2;
③若点D在A点左侧时,如图:
∴BC=CD﹣BD
=2DN﹣2DM
=3(DN﹣DM)
=2MN,
∴=2,
综上所述,=3.
18.【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图1所示的位置,请回答下面的问题.
(1)如果重叠在一起∠BOC=30°则∠AOD= 150° .
(2)若将∠COD绕点O旋转,使重叠在一起的∠BOC=50°,∠AOD= 130° .
(3)图1中∠AOC与∠BOD满足的数量关系是 ∠AOC=∠BOD ,根据是 同角的余角相等 .
【拓展】在图1所示的位置上,继续将∠COD绕点O旋转,得到如图2所示的位置
(4)如果∠BOC=x°,则∠AOD= 180°﹣x° .(用含x的式子表示)
(5)此时图2中∠AOC与∠BOD始终满足的数量关系是 ∠AOC=∠BOD .
(6)【结论】山上述的探究过程可知,三角板COD绕重合点O旋转.不论旋转到任何位置时,∠AOD与∠BOC始终满足的数量关系是 ∠AOD+∠BOC=180° .
【答案】(1)150°;
(2)130°;
(3)∠AOC=∠BOD,同角的余角相等;
(4)180°﹣x°;
(5)∠AOC=∠BOD;
(6)∠AOD+∠BOC=180°.
【解答】解:(1)∵∠AOB=90°,∠COD=90°,
∴∠AOD=∠AOB+∠COD﹣∠BOC
=90°+90°﹣30°
=150°;
故答案为:150°;
(2)∵∠AOB=90°,∠BOC=50°,
∴∠AOC=40°,
∵∠COD=90°,
∴∠AOD=∠AOC+∠COD=130°;
故答案为:130°;
(3)∵∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,
∴∠AOC=∠BOD(同角的余角相等);
故答案为:∠AOC=∠BOD,同角的余角相等;
(4)∵∠AOB=90°,∠COD=90°,
∴∠AOD=∠AOB+∠COD﹣∠BOC
=90°+90°﹣x°
=180°﹣x°;
故答案为:180°﹣x°;
(5)∵∠AOB=∠COD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD;
故答案为:∠AOC=∠BOD;
(6)∵∠AOB=∠COD=90°,
∴∠AOB+∠COD=180°,
∴∠AOD+∠BOC=360°﹣180°=180°,
∴由上述的探究过程可知,三角板COD绕重合点O旋转,∠AOD与∠BOC始终满足的数量关系是:∠AOD+∠BOC=180°.
故答案为:∠AOD+∠BOC=180°.
湘教新版七年级上册数学
一.选择题(共9小题)
1.下列物体的形状类似于球的是( )
A.乒乓球 B.羽毛球 C.茶杯 D.白炽灯泡
2.三棱锥有( )个面.
A.3 B.4 C.5 D.6
3.如图,∠ACB=90°,CD⊥AB( )
A.2对 B.3对 C.4对 D.5对
4.已知:在同一平面内,∠AOB=60°,∠BOC=20°,则∠BOM=( )
A.20° B.40° C.20°或40° D.20°或60°
5.一个钝角减去一个锐角所得的差是( )
A.直角 B.锐角
C.钝角 D.以上三种都有可能
6.已知正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周( )
A.27cm3 B.27πcm3 C.18cm3 D.18πcm3
7.如图,将一副三角板叠放在一起,使直角顶点重合于C点( )
A.90° B.60° C.120° D.180°
8.已知∠AOB=75°,以O为端点作射线OC,使∠AOC=48°( )
A.123° B.123°和27° C.23° D.27°
9.如图,带有弧线的角是用一副三角板拼成的,这个角的度数为( )
A.60° B.15° C.45° D.105°
二.填空题(共5小题)
10.已知∠α=55°,则∠α的余角度数是 .
11.若∠1=20°18',∠2=20°15'30″,∠3=20.25°,顺序为 .
12.已知直线l上有A,B,C,D四点,且AB=7,则CD的长为 .
13.三棱柱由 个面围成.
14.小丽在“红色研学”活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的“奔跑者”形象来激励自己.已知图1正方形纸片的边长为4,则“奔跑者”两脚之间的跨度,即AB .
三.解答题(共4小题)
15.如图,点C在线段AB上,点D是线段AB的中点,BC=3cm,求线段CD的长度.
16.如图,点A,O,E在同一直线上,∠EOD=25°,OD平分∠COE,
(1)写出图中所有互补的角.
(2)求∠COB的度数.
17.已知一条直线上从左到右依次有A、B、C三个点.
(1)若BC=10,AC=3AB,直接写出AB的长度为 .
(2)若D是射线BC上一点,M是BD的中点,N是CD的中点,求
18.【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图1所示的位置,请回答下面的问题.
(1)如果重叠在一起∠BOC=30°则∠AOD= .
(2)若将∠COD绕点O旋转,使重叠在一起的∠BOC=50°,∠AOD= .
(3)图1中∠AOC与∠BOD满足的数量关系是 ,根据是 .
【拓展】在图1所示的位置上,继续将∠COD绕点O旋转,得到如图2所示的位置
(4)如果∠BOC=x°,则∠AOD= .(用含x的式子表示)
(5)此时图2中∠AOC与∠BOD始终满足的数量关系是 .
(6)【结论】山上述的探究过程可知,三角板COD绕重合点O旋转.不论旋转到任何位置时,∠AOD与∠BOC始终满足的数量关系是 .
第4章 图形的认识(单元新题测试)湘教新版七年级上册数学
参考答案与试题解析
一.选择题(共9小题)
1.下列物体的形状类似于球的是( )
A.乒乓球 B.羽毛球 C.茶杯 D.白炽灯泡
【答案】A
【解答】解:A、乒乓球的形状类似于球;
B、羽毛球类似于圆锥;
C、茶杯类似于圆柱;
D、白炽灯类似于圆锥加球;
故选:A.
2.三棱锥有( )个面.
A.3 B.4 C.5 D.6
【答案】B
【解答】解:三棱锥有6条棱,有4个面.
故选:B.
3.如图,∠ACB=90°,CD⊥AB( )
A.2对 B.3对 C.4对 D.5对
【答案】C
【解答】解:∵∠ACB=90°,
∴∠A与∠B互余,∠ACD与∠DCB互余.
∵CD⊥AB,
∴∠ADC=90°,∠CDB=90°.
∴∠A与∠ACD互余,∠B与∠DCB互余.
故选:C.
4.已知:在同一平面内,∠AOB=60°,∠BOC=20°,则∠BOM=( )
A.20° B.40° C.20°或40° D.20°或60°
【答案】C
【解答】解:如图1,当OC在∠AOB内部时,
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=40°,
∵OM是∠AOC的平分线,
∴∠COM=AOC=20°,
∴∠BOM=∠COM+∠BOC=40°;
如图2,当OC在∠AOB外部时,
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=80°,
∵OM是∠AOC的平分线,
∴,
∴∠BOM=∠COM﹣∠BOC=20°;
综上所述:∠BOM的度数为40°或20°,
故选:C.
5.一个钝角减去一个锐角所得的差是( )
A.直角 B.锐角
C.钝角 D.以上三种都有可能
【答案】D
【解答】解:一个钝角减去一个锐角所得的差可能是直角、也可能是锐角或钝角.
故选:D.
6.已知正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周( )
A.27cm3 B.27πcm3 C.18cm3 D.18πcm3
【答案】B
【解答】解:直线AB为轴,将正方形旋转一周可得圆柱体,底面直径为6cm,
∴所得几何体的体积=38 π 3=27π(cm3),
故选:B.
7.如图,将一副三角板叠放在一起,使直角顶点重合于C点( )
A.90° B.60° C.120° D.180°
【答案】D
【解答】解:∵∠ACB=∠DCE=90°,
∴∠ACE+∠BCE=90°,∠BCE+∠BCD=90°,
∴∠ACE+∠BCE+∠BCE+∠BCD=180°,
∴∠ACE+2∠BCE+∠BCD=180°,
∵∠ACD=∠ACE+∠BCE+∠BCD,
∴∠ACD+∠BCE=180°.
故选:D.
8.已知∠AOB=75°,以O为端点作射线OC,使∠AOC=48°( )
A.123° B.123°和27° C.23° D.27°
【答案】B
【解答】解:如图,
当点C与点C1重合时,∠BOC=∠AOB﹣∠AOC=75°﹣48°=27°;
当点C与点C2重合时,∠BOC=∠AOB+∠AOC=75°+48°=123°.
故选:B.
9.如图,带有弧线的角是用一副三角板拼成的,这个角的度数为( )
A.60° B.15° C.45° D.105°
【答案】B
【解答】解:这个角的度数=60°﹣45°=15°,
故选:B.
二.填空题(共5小题)
10.已知∠α=55°,则∠α的余角度数是 35° .
【答案】见试题解答内容
【解答】解:∵∠α=55°,
∴∠α的余角度数是:90°﹣55°=35°.
故答案为:35°.
11.若∠1=20°18',∠2=20°15'30″,∠3=20.25°,顺序为 ∠1>∠2>∠3 .
【答案】∠1>∠2>∠3.
【解答】解:∵∠3=20.25°=20°15′,
∴∠1>∠6>∠3,
故答案为:∠1>∠7>∠3.
12.已知直线l上有A,B,C,D四点,且AB=7,则CD的长为 4或7或10 .
【答案】4或7或10
【解答】解:如图1,∵AC=BD=1.2,
∴CD=AB﹣AC﹣BD=4;
如图2,CD=AC+AB﹣BD=2.5+7﹣3.5=7;
如图7,CD=AB﹣AC+BD=7,
如图4,CD=AC+AB+BD=7.5+7+7.5=10,
综上所述,CD的长为4或3或10,
故答案为:4或7或10.
13.三棱柱由 5 个面围成.
【答案】见试题解答内容
【解答】解:三棱柱是由侧面的3个长方形和上下2个底面组成,共8个面围成的.
故答案为:5.
14.小丽在“红色研学”活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的“奔跑者”形象来激励自己.已知图1正方形纸片的边长为4,则“奔跑者”两脚之间的跨度,即AB .
【答案】.
【解答】解:如图2中,过点E作EI⊥FK于I.
由题意,△ABM,AB=BM=2,FK=4,
∵EI⊥FK,
∴KI=IF,
∴EI=FK=2,
∵MJ∥EI,
∴==,
∴MJ=,
∵AB∥CD,
∴AB与CD之间的距离=5++4=,
故答案为:
三.解答题(共4小题)
15.如图,点C在线段AB上,点D是线段AB的中点,BC=3cm,求线段CD的长度.
【答案】1.5 cm.
【解答】解:∵AC=6cm,BC=3cm,
∴AB=AC+BC=6+3=9(cm),
∵点D是线段AB的中点,
∴AD=AB=,
∴CD=AC﹣AD=6﹣4.6=1.5(cm),
故线段CD的长度为2.5 cm.
16.如图,点A,O,E在同一直线上,∠EOD=25°,OD平分∠COE,
(1)写出图中所有互补的角.
(2)求∠COB的度数.
【答案】见试题解答内容
【解答】解:(1)∵点A,O,E在同一直线上,
∴∠AOB+∠BOE=180°,∠AOC+∠COE=180°,
∠AOD+∠DOE=180°,
∵OD平分∠COE,
∴∠COD=∠DOE,
∴∠COD+∠AOD=180°.
∴图中所有互补的角有:∠AOB与∠BOE,∠AOC与∠COE,∠COD与∠AOD.
(2)因为∠EOD=25°,OD平分∠COE,
所以∠COE=2∠EOD=50°,
所以∠COB=180°﹣∠AOB﹣∠COE,
=180°﹣40°﹣50°=90°.
17.已知一条直线上从左到右依次有A、B、C三个点.
(1)若BC=10,AC=3AB,直接写出AB的长度为 5 .
(2)若D是射线BC上一点,M是BD的中点,N是CD的中点,求
【答案】(1)5;
(2)=2.
【解答】解:(1)如图:
∵AC=AB+BC,AC=3AB,
∴3AB=AB+BC
∵BC=10,
∴7AB=10,
∴AB=5,
故答案为:5;
(2)∵点M为BD的中点,点N为CD的中点,
∴BD=4BM=2DM,CD=2DN=5CN,
若点D在BC之间时,如图:
∴BC=BD+CD=2MD+2DN=8MN,
∴=2,
②若点D在AB之间时,如图:
∴BC=DC﹣DB
=2DN﹣6DM
=2(DN﹣DM)
=2MN,
∴=2;
③若点D在A点左侧时,如图:
∴BC=CD﹣BD
=2DN﹣2DM
=3(DN﹣DM)
=2MN,
∴=2,
综上所述,=3.
18.【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图1所示的位置,请回答下面的问题.
(1)如果重叠在一起∠BOC=30°则∠AOD= 150° .
(2)若将∠COD绕点O旋转,使重叠在一起的∠BOC=50°,∠AOD= 130° .
(3)图1中∠AOC与∠BOD满足的数量关系是 ∠AOC=∠BOD ,根据是 同角的余角相等 .
【拓展】在图1所示的位置上,继续将∠COD绕点O旋转,得到如图2所示的位置
(4)如果∠BOC=x°,则∠AOD= 180°﹣x° .(用含x的式子表示)
(5)此时图2中∠AOC与∠BOD始终满足的数量关系是 ∠AOC=∠BOD .
(6)【结论】山上述的探究过程可知,三角板COD绕重合点O旋转.不论旋转到任何位置时,∠AOD与∠BOC始终满足的数量关系是 ∠AOD+∠BOC=180° .
【答案】(1)150°;
(2)130°;
(3)∠AOC=∠BOD,同角的余角相等;
(4)180°﹣x°;
(5)∠AOC=∠BOD;
(6)∠AOD+∠BOC=180°.
【解答】解:(1)∵∠AOB=90°,∠COD=90°,
∴∠AOD=∠AOB+∠COD﹣∠BOC
=90°+90°﹣30°
=150°;
故答案为:150°;
(2)∵∠AOB=90°,∠BOC=50°,
∴∠AOC=40°,
∵∠COD=90°,
∴∠AOD=∠AOC+∠COD=130°;
故答案为:130°;
(3)∵∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,
∴∠AOC=∠BOD(同角的余角相等);
故答案为:∠AOC=∠BOD,同角的余角相等;
(4)∵∠AOB=90°,∠COD=90°,
∴∠AOD=∠AOB+∠COD﹣∠BOC
=90°+90°﹣x°
=180°﹣x°;
故答案为:180°﹣x°;
(5)∵∠AOB=∠COD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD;
故答案为:∠AOC=∠BOD;
(6)∵∠AOB=∠COD=90°,
∴∠AOB+∠COD=180°,
∴∠AOD+∠BOC=360°﹣180°=180°,
∴由上述的探究过程可知,三角板COD绕重合点O旋转,∠AOD与∠BOC始终满足的数量关系是:∠AOD+∠BOC=180°.
故答案为:∠AOD+∠BOC=180°.
同课章节目录
