探索勾股定理

课件23张PPT。是否有外星人存在呢?如果有的话,我们怎么样才能与”外星人”接触呢?
??? 希腊1955年为纪念毕达哥拉斯学派发行的纪念邮票。 三角形问题1:三角形按角可以怎么分类?
答:锐角三角形,直角三角形,钝角三角形.
问题2:直角三角形有什么特点?
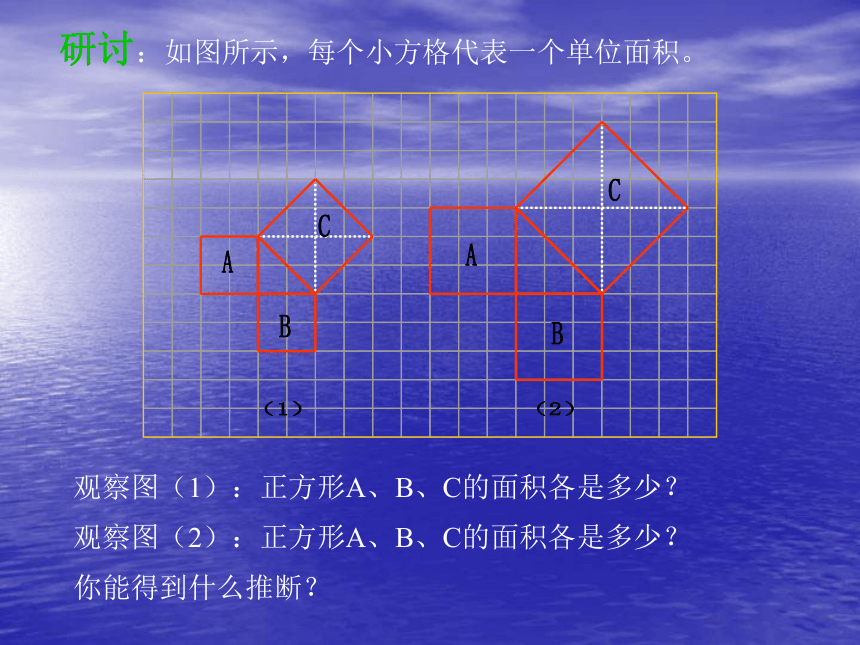
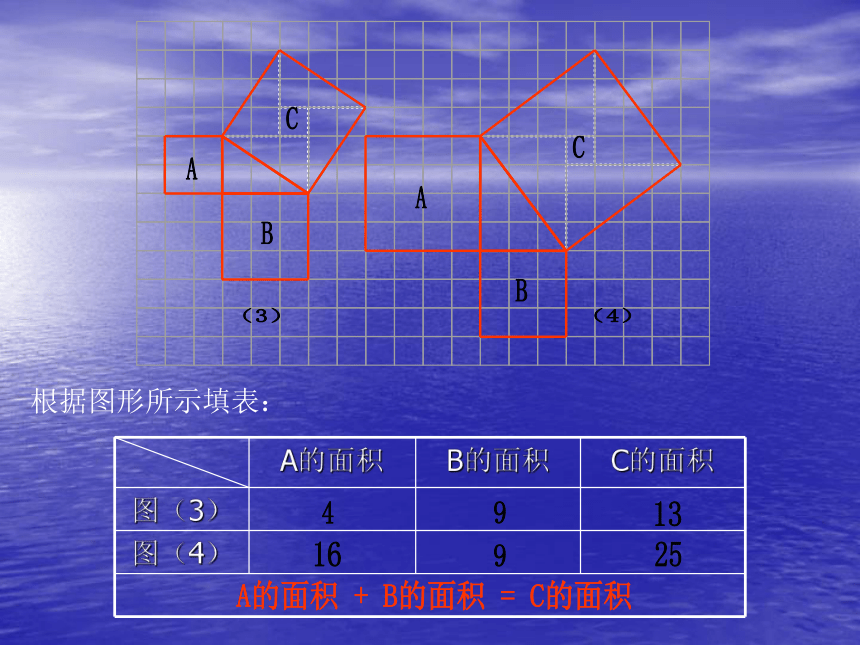
答:有一个直角.探 索 勾 股 定 理研讨：如图所示，每个小方格代表一个单位面积。观察图（1）：正方形A、B、C的面积各是多少？观察图（2）：正方形A、B、C的面积各是多少？你能得到什么推断？根据图形所示填表：A的面积 + B的面积 = C的面积练习：
1、求下列图中字母所表示的正方形的面积议一议：（１）你能用三角形的边长表示正方形的面积吗？
（２）你能发现直角三角形三边的长度之间存在什么关系吗？
（３）分别以５厘米，１２厘米为直角边作出一个直角三角形，并测量斜边的长度．（２）中的规律对这个三角形仍然成立吗？正方形A的面积+正方形B的面积=正方形C的面积2.判断题:(1).如果三角形的三边长分别为a,b,c，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　（　）
(2).如果直角三角形的三边长分别为a,b,c，则
　　　　　　　　　　　　　　　　　　　　　　　　　　（　）
答案：(１). ×　　　　　　(２). ×
3.求出下列直角三角形中未知边的长度4.填空:(1).在△ABC中, ∠C=90°，c=25,b=15,则a=＿＿＿＿.
(2). 三角形的三个内角之比为：１：２：３，则此三角形是＿＿＿．若此三角形的三边长分别为a,b,c,则它们的关系是＿＿＿＿．
答案：(１).２０　　(２).直角三角形
问题：在第(２)题中，如果把　１：２：３改成３：２：１，答案会一样吗？
3. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少米? 5. 想一想： 小明妈妈买了一部29英寸（74厘米）的电视机，小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你同意他的想法吗？你能解释这是为什么吗？定 理 的 历 史 及 证 明★ 公元前11世纪，周公与商高的对话（记录于公元前1世纪《周髀算经》）中提出“勾三、股四、弦五”。——勾股定理、商高定理★ 《周髀算经》中还记载了公元前六、七世纪的荣方与陈子的对话，再次提到勾股定理。——陈子定理★ 公元前600年左右，古希腊的毕达哥拉斯学派发现勾股定理，命名为“毕达哥拉斯定理” （百牛定理），而且给出了证明。★ 古巴比仑人在公元前19世纪也发现此定理。★ 中国最早给出定理证明的是公元3世纪三国时吴国数学家赵爽（赵君卿）。★ 定理从提出到现在的两千多年中，已经找到证明400多种，由鲁密斯搜集整理的《毕达哥拉斯》一书中就给出370种不同证法。回忆与小结：１.这节课你的收获是什么？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
２.理解“勾股定理”应该注意什么问题？
３.你觉得“勾股定理”有用吗？再见！证法一：（赵爽证法）正方形ABCD的面积为 还可以认为是四个三角形与一个小正方形的和，即∴ ∴证法二：（毕达哥拉斯证法） 如图，两个全等的正方形，双方都去掉四个全等带阴
影的直角三角形后，两正方形中剩下的部分面积应相等。
即：证法三：（伽菲尔德证法1876年） 如图，Rt△ABE≌Rt△ECD，
可知∠AED=90°；梯形ABCD的面积＝梯形ABCD的面积＝∴∴