九年级数学第三次复习检测题(全国)(无答案)
文档属性
| 名称 | 九年级数学第三次复习检测题(全国)(无答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 69.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-22 00:00:00 | ||
图片预览



文档简介
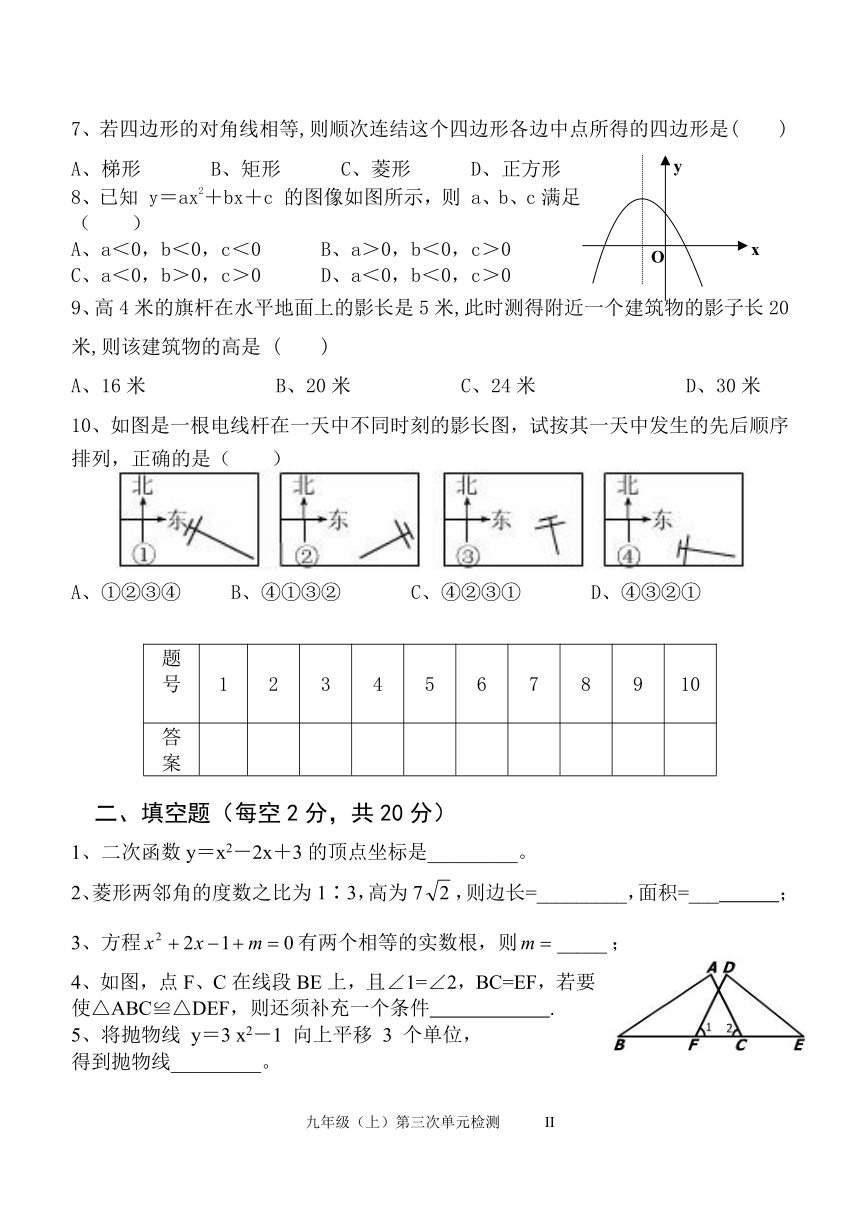
九年级(上)数学第三次复习检测题
班级___ 姓名___
(时间:120分钟 满分:150分)
A卷(100分)
一、选择题(每题3分,共30分,请将选择题答案填在题后表格中)
1、已知2是关于x的方程的一个解,则k的值是( )
A、 3 B、 4 C、 5 D、 6
2、将方程左边变成完全平方式后,方程是 ( )
A、 B、 C、 D、
3、在△ABC中,∠C=90°,,则sinB的值是( )
A. B. C. D.
4、有一实物如图,那么它的主视图 ( )
5、 若反比例函数的图象经过(2,-2),(m,1),则m=( )
A、1 B、-1 C、4 D、-4
6、下列性质中正方形具有而矩形没有的是( )
A、对角线互相平分 B、对角线相等
C、对角线互相垂直 D、四个角都是直角
7、若四边形的对角线相等,则顺次连结这个四边形各边中点所得的四边形是( )
A、梯形 B、矩形 C、菱形 D、正方形
8、已知 y=ax2+bx+c 的图像如图所示,则 a、b、c满足( )
A、a<0,b<0,c<0 B、a>0,b<0,c>0
C、a<0,b>0,c>0 D、a<0,b<0,c>0
9、高4米的旗杆在水平地面上的影长是5米,此时测得附近一个建筑物的影子长20米,则该建筑物的高是 ( )
A、16米 B、20米 C、24米 D、30米
10、如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )
A、①②③④ B、④①③② C、④②③① D、④③②①
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(每空2分,共20分)
1、二次函数y=x2-2x+3的顶点坐标是_________。
2、菱形两邻角的度数之比为1∶3,高为7,则边长=_________,面积=___ ;
3、方程有两个相等的实数根,则;
4、如图,点F、C在线段BE上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还须补充一个条件 .
5、将抛物线 y=3 x2-1 向上平移 3 个单位,
得到抛物线_________。
6、若点A(-2,y1)、B(-1,y2)、C(1,y3)在反比例函数的图像上, 则y1、y2、y3的大小关系是_________。
7、如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3= .
8、已知一个等腰三角形有一个角为50o,则顶角是 = .
9、小军同学家开了一个商店,今年1月份的利润是1000元,3月份的利润是1210元,请你帮助小军同学算一算,他家的这个商店这两个月的利润平均月增长率是___________;
三、计算题(每题4分,共24分)
(1)x2-2x=0; (2)x2+3x-4=0;
(3) (4);
(5)
(6)
四、(本题8分)
如图,在某建筑物AC上,挂着“做文明市民”的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为,求宣传条幅BC的长.
五、(本题8分)
如图,在中,是边上的一点,是的中点,过点作的平行线交的延长线于,且,连结.
(1)求证:是的中点.
(2)如果,试判断四边形的形状,并证明你的结论.
六、(本题10分)
已知反比例函数和一次函数y=kx +b,其中一次函数的图象经过(1,1)和(-1,5)两点.
(1)求反比例函数和一次函数的解析式;
(2)一次函数的图象与反比例函数的图象交于A、B两点,求△AOB的面积;
(3)写出反比例函数值大于一次函数值的x的取值范围。
B卷(共50分)
一、填空题(本题20分)
1、已知
2、已知二次函数的图象如图所示,有下列5个结论:① ;② ;③ ;④ ;⑤2a+b=0其中正确的结论有 (填序号)
3、三角形三边长为6、7、8、,则这个三角形的面积是
4、如图,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为
5、如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点。如果A点的坐标为(2,0),点C、D分别在第一、三象限,且OA=OB=AC=BD;则反比例函数的表达式为
二、解答题(本题8分)
某商店经销一种销售成本为每千克40元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克, 销售单价每涨一元,月销售量就减少10千克。针对这种情况,解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润.
(2)设销售单价为每千克为X元,月销售利润为Y元,求Y与X的函数关系式;并写出自变量的取值范围.
(3)在月销售成本不超过10000元的情况下,使月利润达到8000元,销售单价应定为多少
三、(本题10分)
如图,在一块三角形区域ABC中,∠C=90°,边AC=8,BC=6,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.
(1)求△ABC中AB边上的高h;
(2)设DG=x,当x取何值时,水池DEFG的面积最大?
(3)实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使三角形区域中欲建的最大矩形水池能避开大树.
四、(本题12分)
如图:四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点从出发以每秒2个单位长度的速度向运动;点从同时出发,以每秒1个单位长度的速度向运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点作垂直轴于点,连结AC交NP于Q,连结MQ.
(1)点______(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.
3
2
1
O
y
x
A B C D
九年级(上)第三次单元检测 VI
班级___ 姓名___
(时间:120分钟 满分:150分)
A卷(100分)
一、选择题(每题3分,共30分,请将选择题答案填在题后表格中)
1、已知2是关于x的方程的一个解,则k的值是( )
A、 3 B、 4 C、 5 D、 6
2、将方程左边变成完全平方式后,方程是 ( )
A、 B、 C、 D、
3、在△ABC中,∠C=90°,,则sinB的值是( )
A. B. C. D.
4、有一实物如图,那么它的主视图 ( )
5、 若反比例函数的图象经过(2,-2),(m,1),则m=( )
A、1 B、-1 C、4 D、-4
6、下列性质中正方形具有而矩形没有的是( )
A、对角线互相平分 B、对角线相等
C、对角线互相垂直 D、四个角都是直角
7、若四边形的对角线相等,则顺次连结这个四边形各边中点所得的四边形是( )
A、梯形 B、矩形 C、菱形 D、正方形
8、已知 y=ax2+bx+c 的图像如图所示,则 a、b、c满足( )
A、a<0,b<0,c<0 B、a>0,b<0,c>0
C、a<0,b>0,c>0 D、a<0,b<0,c>0
9、高4米的旗杆在水平地面上的影长是5米,此时测得附近一个建筑物的影子长20米,则该建筑物的高是 ( )
A、16米 B、20米 C、24米 D、30米
10、如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )
A、①②③④ B、④①③② C、④②③① D、④③②①
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(每空2分,共20分)
1、二次函数y=x2-2x+3的顶点坐标是_________。
2、菱形两邻角的度数之比为1∶3,高为7,则边长=_________,面积=___ ;
3、方程有两个相等的实数根,则;
4、如图,点F、C在线段BE上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还须补充一个条件 .
5、将抛物线 y=3 x2-1 向上平移 3 个单位,
得到抛物线_________。
6、若点A(-2,y1)、B(-1,y2)、C(1,y3)在反比例函数的图像上, 则y1、y2、y3的大小关系是_________。
7、如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3= .
8、已知一个等腰三角形有一个角为50o,则顶角是 = .
9、小军同学家开了一个商店,今年1月份的利润是1000元,3月份的利润是1210元,请你帮助小军同学算一算,他家的这个商店这两个月的利润平均月增长率是___________;
三、计算题(每题4分,共24分)
(1)x2-2x=0; (2)x2+3x-4=0;
(3) (4);
(5)
(6)
四、(本题8分)
如图,在某建筑物AC上,挂着“做文明市民”的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为,求宣传条幅BC的长.
五、(本题8分)
如图,在中,是边上的一点,是的中点,过点作的平行线交的延长线于,且,连结.
(1)求证:是的中点.
(2)如果,试判断四边形的形状,并证明你的结论.
六、(本题10分)
已知反比例函数和一次函数y=kx +b,其中一次函数的图象经过(1,1)和(-1,5)两点.
(1)求反比例函数和一次函数的解析式;
(2)一次函数的图象与反比例函数的图象交于A、B两点,求△AOB的面积;
(3)写出反比例函数值大于一次函数值的x的取值范围。
B卷(共50分)
一、填空题(本题20分)
1、已知
2、已知二次函数的图象如图所示,有下列5个结论:① ;② ;③ ;④ ;⑤2a+b=0其中正确的结论有 (填序号)
3、三角形三边长为6、7、8、,则这个三角形的面积是
4、如图,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为
5、如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点。如果A点的坐标为(2,0),点C、D分别在第一、三象限,且OA=OB=AC=BD;则反比例函数的表达式为
二、解答题(本题8分)
某商店经销一种销售成本为每千克40元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克, 销售单价每涨一元,月销售量就减少10千克。针对这种情况,解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润.
(2)设销售单价为每千克为X元,月销售利润为Y元,求Y与X的函数关系式;并写出自变量的取值范围.
(3)在月销售成本不超过10000元的情况下,使月利润达到8000元,销售单价应定为多少
三、(本题10分)
如图,在一块三角形区域ABC中,∠C=90°,边AC=8,BC=6,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.
(1)求△ABC中AB边上的高h;
(2)设DG=x,当x取何值时,水池DEFG的面积最大?
(3)实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使三角形区域中欲建的最大矩形水池能避开大树.
四、(本题12分)
如图:四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点从出发以每秒2个单位长度的速度向运动;点从同时出发,以每秒1个单位长度的速度向运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点作垂直轴于点,连结AC交NP于Q,连结MQ.
(1)点______(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.
3
2
1
O
y
x
A B C D
九年级(上)第三次单元检测 VI
同课章节目录
