21.6 综合与实践 获得最大利润 课时同步培优练习(含答案)2023-2024学年沪科版九年级数学上册
文档属性
| 名称 | 21.6 综合与实践 获得最大利润 课时同步培优练习(含答案)2023-2024学年沪科版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 63.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 14:34:27 | ||
图片预览

文档简介
21.6 综合与实践 获得最大利润 课时同步培优练习
一、选择题(在每小题列出的选项中,选出符合题目的一项)
1. 关于二次函数的最大值或最小值,下列说法正确的是( )
A. 有最大值 B. 有最小值 C. 有最大值 D. 有最小值
2. 关于二次函数的最大值或最小值,下列叙述中正确的是( )
A. 当时,有最大值 B. 当时,有最小值
C. 当时,有最小值 D. 当时,有最大值
3. 由二次函数可知( )
A. 其图象的开口向下 B. 其图象的对称轴为
C. 其最大值为 D. 当时,随的增大而减小
4. 若二次函数有最小值为,则的值为( )
A. B. C. D.
5. 已知二次函数,当,下列说法正确的是( )
A. 有最小值 B. 有最小值 C. 有最小值 D. 有最大值
6. 某旅行社在“五一”期间接团去外地旅游,经计算,所获营业额元与旅行团人数人之间满足关系式,要使所获营业额最大,则此旅行团应有( )
A. 人 B. 人 C. 人 D. 人
7. 将进货单价为元的某种商品按元售出时,能卖出个,单价每上涨元,其销售量就减小个,为了获得最大利润,售价应定为每件( )
A. 元 B. 元 C. 元 D. 元
8. 将进货单价为元的某种商品按零售价每个元出售时,每天能卖出个.若这种商品零售价在一定范围内每降价元,日销售量就增加个,为获得最大利润,应降价( )
A. 元 B. 元 C. 元 D. 元
9. 向空中发射一枚炮弹,经秒后的高度为米,且时间与高度的关系为、若此炮弹在第秒与第秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A. 第秒 B. 第秒 C. 第秒 D. 第秒
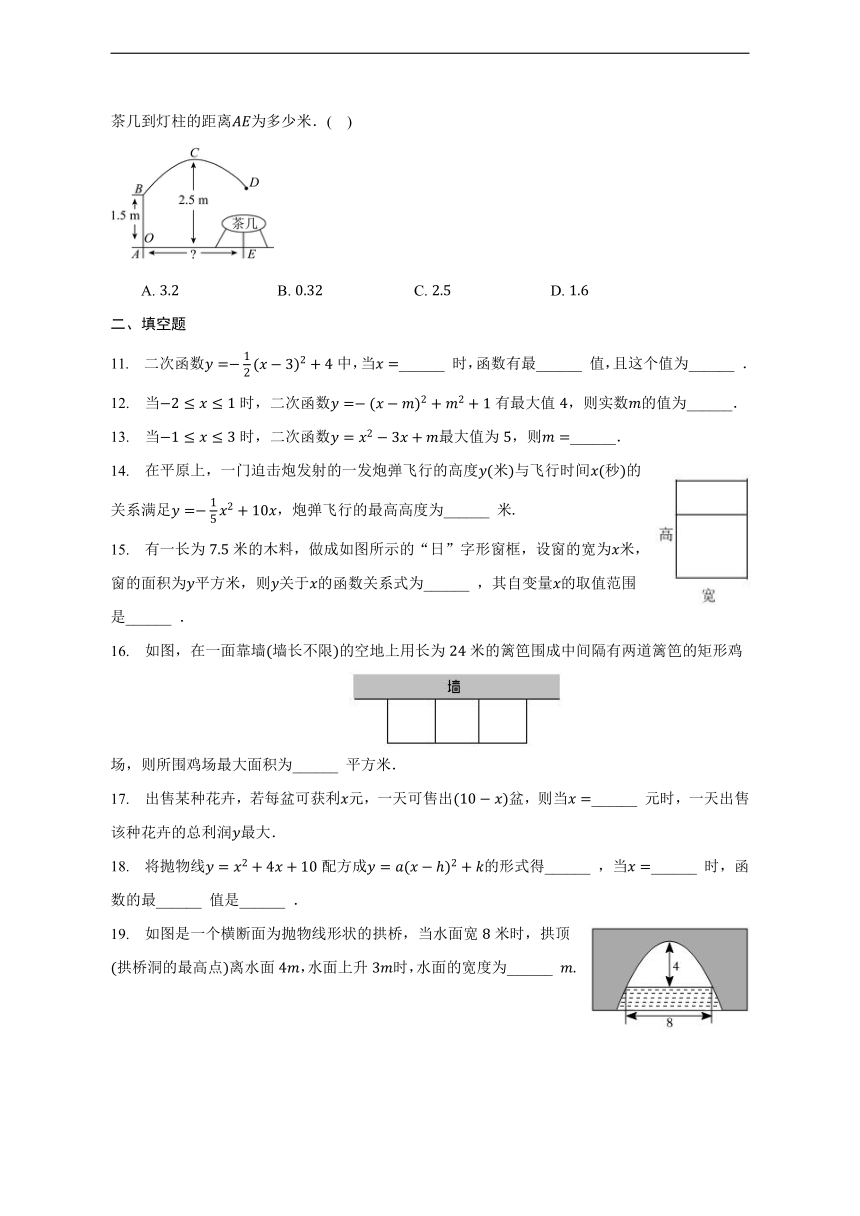
10. 如图是一款抛物线型落地灯筒示意图,防滑螺母为抛物线支架的最高点,灯罩距离地面米,最高点距灯柱的水平距离为米,灯柱为米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离为多少米.( )
A. B. C. D.
二、填空题
11. 二次函数中,当______ 时,函数有最______ 值,且这个值为______ .
12. 当时,二次函数有最大值,则实数的值为______.
13. 当时,二次函数最大值为,则______.
14. 在平原上,一门迫击炮发射的一发炮弹飞行的高度米与飞行时间秒的关系满足,炮弹飞行的最高高度为______ 米
15. 有一长为米的木料,做成如图所示的“日”字形窗框,设窗的宽为米,窗的面积为平方米,则关于的函数关系式为______ ,其自变量的取值范围是______ .
16. 如图,在一面靠墙墙长不限的空地上用长为米的篱笆围成中间隔有两道篱笆的矩形鸡场,则所围鸡场最大面积为______ 平方米.
17. 出售某种花卉,若每盆可获利元,一天可售出盆,则当______ 元时,一天出售该种花卉的总利润最大.
18. 将抛物线配方成的形式得______ ,当______ 时,函数的最______ 值是______ .
19. 如图是一个横断面为抛物线形状的拱桥,当水面宽米时,拱顶拱桥洞的最高点离水面,水面上升时,水面的宽度为______
20. 如图,一名学生推铅球,铅球行进高度单位:与水平距离单位:之间的关系是,则铅球推出的距离______
三、解答题(解答应写出文字说明,证明过程或演算步骤)
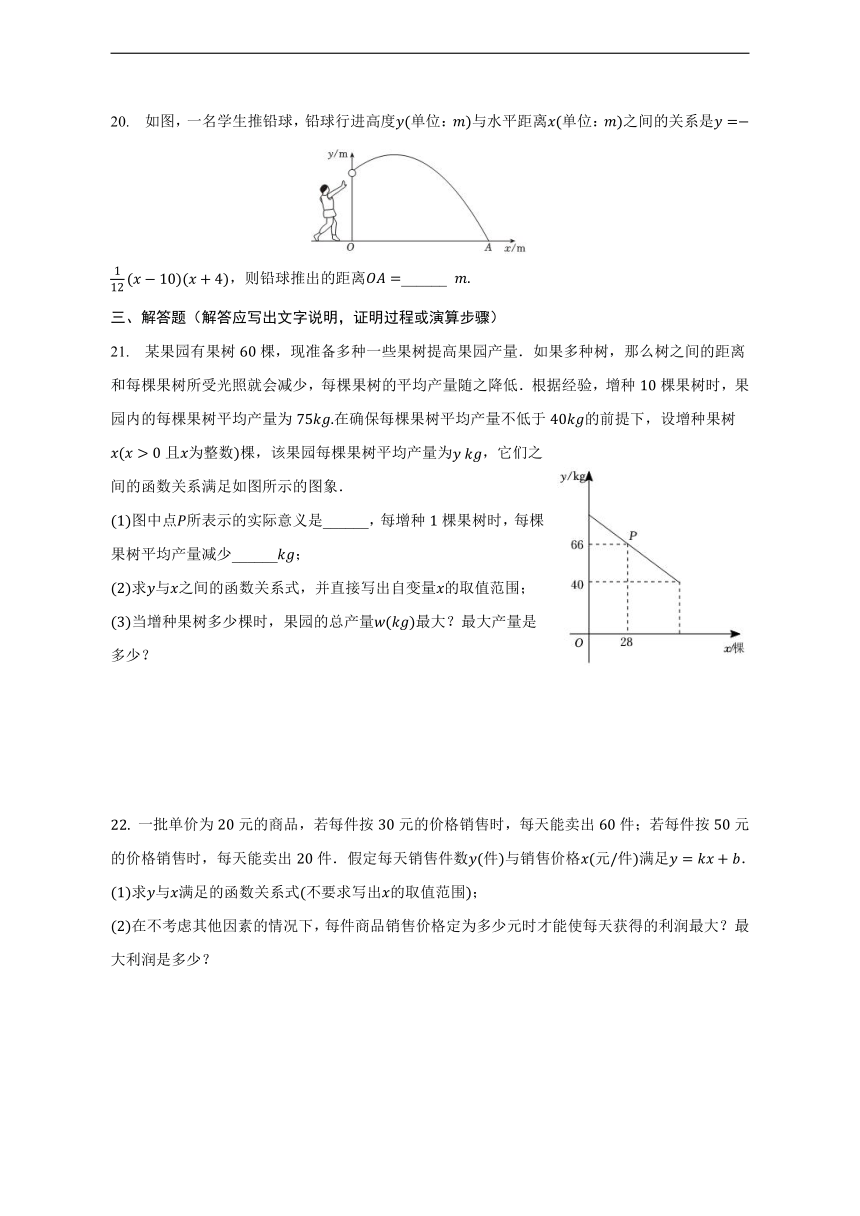
21. 某果园有果树棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种棵果树时,果园内的每棵果树平均产量为在确保每棵果树平均产量不低于的前提下,设增种果树且为整数棵,该果园每棵果树平均产量为,它们之间的函数关系满足如图所示的图象.
图中点所表示的实际意义是______,每增种棵果树时,每棵果树平均产量减少______;
求与之间的函数关系式,并直接写出自变量的取值范围;
当增种果树多少棵时,果园的总产量最大?最大产量是多少?
一批单价为元的商品,若每件按元的价格销售时,每天能卖出件;若每件按元的价格销售时,每天能卖出件.假定每天销售件数件与销售价格元件满足.
求与满足的函数关系式不要求写出的取值范围;
在不考虑其他因素的情况下,每件商品销售价格定为多少元时才能使每天获得的利润最大?最大利润是多少?
某游乐场的圆形喷水池中心有一雕塑,从点向四周喷水,喷出的水柱为抛物线,且形状相同如图,以水平方向为轴,点为原点建立直角坐标系,点在轴上,轴上的点,为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为.
求雕塑高;
求落水点,之间的距离;
若需要在上的点处竖立雕塑,,,问:顶部是否会碰到水柱?请通过计算说明.
“互联网”时代,网上购物备受消费者青睐,某网店专售一款休闲裤,其成本为每条
元,当售价为每条元时,每月可销售条.为了吸引更多顾客,该网店采取降价措施,据市场调查反映:销售单价每降元,每月可多销售条,设每条裤子的售价为元为正整数,每月的销售量为条.
直接写出与的函数关系式;
设该网店每月获得的利润为元,当售价为多少元时,每月获得的利润最大,最大利润是多少?
该网店店主热心公益事业,决定每月从利润中捐出元资助贫困学生,为了保证捐款后每月利润为元,且让消费者得到最大的实惠,休闲裤的销售单价定为多少?
21.6 综合与实践获得最大利润课时同步培优练习答案
2. 3. 4. 5.
6. 7. 8. 9. 10.
11. 大 12. 或 13. 14.
15. 16. 17.
18. 小 19. 20.
21. 增种果树棵,每棵果树平均产量为
22. 解:根据题意,得:
,
解得:.
因此与的函数关系式为;
设每件商品销售价格定为元时,每天获得的利润为元,
根据题意,得
,
答:当销售单价定为元时,每天获得的利润最大,最大利润是元.
23. 解:当时,,
点的坐标为,
雕塑高
当时,,
解得:舍去,,
点的坐标为,
.
从点向四周喷水,喷出的水柱为抛物线,且形状相同,
,
.
当时,,
点在抛物线上.
又,
顶部会碰到水柱.
24. 解:由题意可得:
,
与的函数关系式为;
由题意,得:
,
,抛物线开口向下,
有最大值,即当时,,
当售价元时,每月获得最大利润为元;
由题意得:
,
解得,,
抛物线开口向下,对称轴为直线,
当时,符合该网店要求,
要让消费者得到最大的实惠,
.
当销售单价定为元时,既符合网店要求,又能让顾客得到最大实惠.
一、选择题(在每小题列出的选项中,选出符合题目的一项)
1. 关于二次函数的最大值或最小值,下列说法正确的是( )
A. 有最大值 B. 有最小值 C. 有最大值 D. 有最小值
2. 关于二次函数的最大值或最小值,下列叙述中正确的是( )
A. 当时,有最大值 B. 当时,有最小值
C. 当时,有最小值 D. 当时,有最大值
3. 由二次函数可知( )
A. 其图象的开口向下 B. 其图象的对称轴为
C. 其最大值为 D. 当时,随的增大而减小
4. 若二次函数有最小值为,则的值为( )
A. B. C. D.
5. 已知二次函数,当,下列说法正确的是( )
A. 有最小值 B. 有最小值 C. 有最小值 D. 有最大值
6. 某旅行社在“五一”期间接团去外地旅游,经计算,所获营业额元与旅行团人数人之间满足关系式,要使所获营业额最大,则此旅行团应有( )
A. 人 B. 人 C. 人 D. 人
7. 将进货单价为元的某种商品按元售出时,能卖出个,单价每上涨元,其销售量就减小个,为了获得最大利润,售价应定为每件( )
A. 元 B. 元 C. 元 D. 元
8. 将进货单价为元的某种商品按零售价每个元出售时,每天能卖出个.若这种商品零售价在一定范围内每降价元,日销售量就增加个,为获得最大利润,应降价( )
A. 元 B. 元 C. 元 D. 元
9. 向空中发射一枚炮弹,经秒后的高度为米,且时间与高度的关系为、若此炮弹在第秒与第秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A. 第秒 B. 第秒 C. 第秒 D. 第秒
10. 如图是一款抛物线型落地灯筒示意图,防滑螺母为抛物线支架的最高点,灯罩距离地面米,最高点距灯柱的水平距离为米,灯柱为米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离为多少米.( )
A. B. C. D.
二、填空题
11. 二次函数中,当______ 时,函数有最______ 值,且这个值为______ .
12. 当时,二次函数有最大值,则实数的值为______.
13. 当时,二次函数最大值为,则______.
14. 在平原上,一门迫击炮发射的一发炮弹飞行的高度米与飞行时间秒的关系满足,炮弹飞行的最高高度为______ 米
15. 有一长为米的木料,做成如图所示的“日”字形窗框,设窗的宽为米,窗的面积为平方米,则关于的函数关系式为______ ,其自变量的取值范围是______ .
16. 如图,在一面靠墙墙长不限的空地上用长为米的篱笆围成中间隔有两道篱笆的矩形鸡场,则所围鸡场最大面积为______ 平方米.
17. 出售某种花卉,若每盆可获利元,一天可售出盆,则当______ 元时,一天出售该种花卉的总利润最大.
18. 将抛物线配方成的形式得______ ,当______ 时,函数的最______ 值是______ .
19. 如图是一个横断面为抛物线形状的拱桥,当水面宽米时,拱顶拱桥洞的最高点离水面,水面上升时,水面的宽度为______
20. 如图,一名学生推铅球,铅球行进高度单位:与水平距离单位:之间的关系是,则铅球推出的距离______
三、解答题(解答应写出文字说明,证明过程或演算步骤)
21. 某果园有果树棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种棵果树时,果园内的每棵果树平均产量为在确保每棵果树平均产量不低于的前提下,设增种果树且为整数棵,该果园每棵果树平均产量为,它们之间的函数关系满足如图所示的图象.
图中点所表示的实际意义是______,每增种棵果树时,每棵果树平均产量减少______;
求与之间的函数关系式,并直接写出自变量的取值范围;
当增种果树多少棵时,果园的总产量最大?最大产量是多少?
一批单价为元的商品,若每件按元的价格销售时,每天能卖出件;若每件按元的价格销售时,每天能卖出件.假定每天销售件数件与销售价格元件满足.
求与满足的函数关系式不要求写出的取值范围;
在不考虑其他因素的情况下,每件商品销售价格定为多少元时才能使每天获得的利润最大?最大利润是多少?
某游乐场的圆形喷水池中心有一雕塑,从点向四周喷水,喷出的水柱为抛物线,且形状相同如图,以水平方向为轴,点为原点建立直角坐标系,点在轴上,轴上的点,为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为.
求雕塑高;
求落水点,之间的距离;
若需要在上的点处竖立雕塑,,,问:顶部是否会碰到水柱?请通过计算说明.
“互联网”时代,网上购物备受消费者青睐,某网店专售一款休闲裤,其成本为每条
元,当售价为每条元时,每月可销售条.为了吸引更多顾客,该网店采取降价措施,据市场调查反映:销售单价每降元,每月可多销售条,设每条裤子的售价为元为正整数,每月的销售量为条.
直接写出与的函数关系式;
设该网店每月获得的利润为元,当售价为多少元时,每月获得的利润最大,最大利润是多少?
该网店店主热心公益事业,决定每月从利润中捐出元资助贫困学生,为了保证捐款后每月利润为元,且让消费者得到最大的实惠,休闲裤的销售单价定为多少?
21.6 综合与实践获得最大利润课时同步培优练习答案
2. 3. 4. 5.
6. 7. 8. 9. 10.
11. 大 12. 或 13. 14.
15. 16. 17.
18. 小 19. 20.
21. 增种果树棵,每棵果树平均产量为
22. 解:根据题意,得:
,
解得:.
因此与的函数关系式为;
设每件商品销售价格定为元时,每天获得的利润为元,
根据题意,得
,
答:当销售单价定为元时,每天获得的利润最大,最大利润是元.
23. 解:当时,,
点的坐标为,
雕塑高
当时,,
解得:舍去,,
点的坐标为,
.
从点向四周喷水,喷出的水柱为抛物线,且形状相同,
,
.
当时,,
点在抛物线上.
又,
顶部会碰到水柱.
24. 解:由题意可得:
,
与的函数关系式为;
由题意,得:
,
,抛物线开口向下,
有最大值,即当时,,
当售价元时,每月获得最大利润为元;
由题意得:
,
解得,,
抛物线开口向下,对称轴为直线,
当时,符合该网店要求,
要让消费者得到最大的实惠,
.
当销售单价定为元时,既符合网店要求,又能让顾客得到最大实惠.
