湘教新版九年级上册《第1章 反比例函数》单元测试卷(含解析)
文档属性
| 名称 | 湘教新版九年级上册《第1章 反比例函数》单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 270.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 14:14:35 | ||
图片预览



文档简介
湘教新版九年级上册《第1章 反比例函数》2023年单元测试卷
一.选择题(共10小题)
1.下列函数中,y是x的反比例函数的是( )
A. B. C. D.y=x﹣6
2.若a≠0,则一次函数y=ax﹣2与反比例y=函数在同一坐标系中的图象大致是( )
A. B.
C. D.
3.关于反比例函数y=,下列说法错误的是( )
A.图象关于原点对称
B.y随x的增大而减小
C.图象分别位于第一、三象限
D.若点M(a,b)在其图象上,则ab=3
4.若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=﹣上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2
5.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=4,则k2﹣k1的值是( )
A.1 B.2 C.4 D.8
6.如图,△OAB与△AA1B1都是等边三角形,点B,B1依次在函数的图象上,点A,A1依次在x轴的负半轴上,若点B的坐标是,则点A1的坐标是( )
A. B. C. D.
7.已知关于x的方程(x+1)2+(x﹣b)2=2有两个相等的实数根,且反比例函数的图象在每个象限内y随x的增大而增大,那么反比例函数的关系式为( )
A. B. C. D.
8.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,则动力F(单位:N)关于动力臂L(单位:m)的函数解析式正确的是( )
A.F= B.F= C.F= D.F=
9.如图,四边形OABC是平行四边形,点A在反比例函数上,点B在反比例函数上,点C在x轴的正半轴上,则四边形OABC的面积是( )
A.4 B.3 C.2 D.1
10.如图,直线y1=﹣x+2与双曲线y2=相交于A、B两点,已知点A坐标为(m,﹣2m),当x>m时,y2的取值范围为( )
A.y2>4 B.y2<4 C.0<y2<4 D.y2>4或y2<0
二.填空题(共8小题)
11.给出的六个关系式:①x(y+1);②y=;③y=;④y=﹣;⑤y=;⑥y=x﹣1,其中y是x的反比例函数是 .
12.如图,过原点的一条直线与反比例函数y=(k≠0)的图象分别交于A,B两点.若A点的坐标为(a,b),则B点的坐标为 .
13.一次函数y=kx+b(k≠0)的图象的形状是 ,反比例函数y=(k≠0)的图象的形状是 .
14.若反比例函数y=的图象经过点(﹣2,),则此函数的解析式为 .
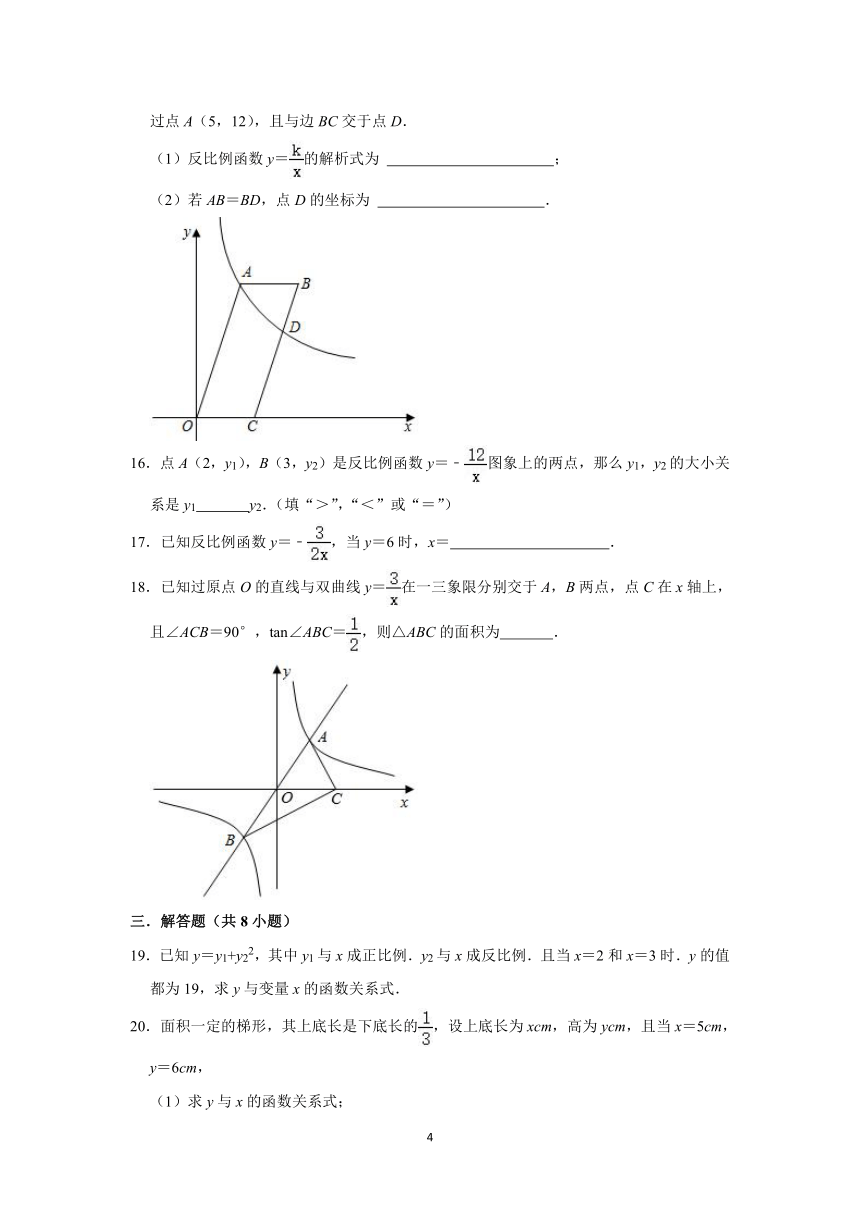
15.如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=(x>0)图象经过点A(5,12),且与边BC交于点D.
(1)反比例函数y=的解析式为 ;
(2)若AB=BD,点D的坐标为 .
16.点A(2,y1),B(3,y2)是反比例函数y=﹣图象上的两点,那么y1,y2的大小关系是y1 y2.(填“>”,“<”或“=”)
17.已知反比例函数y=﹣,当y=6时,x= .
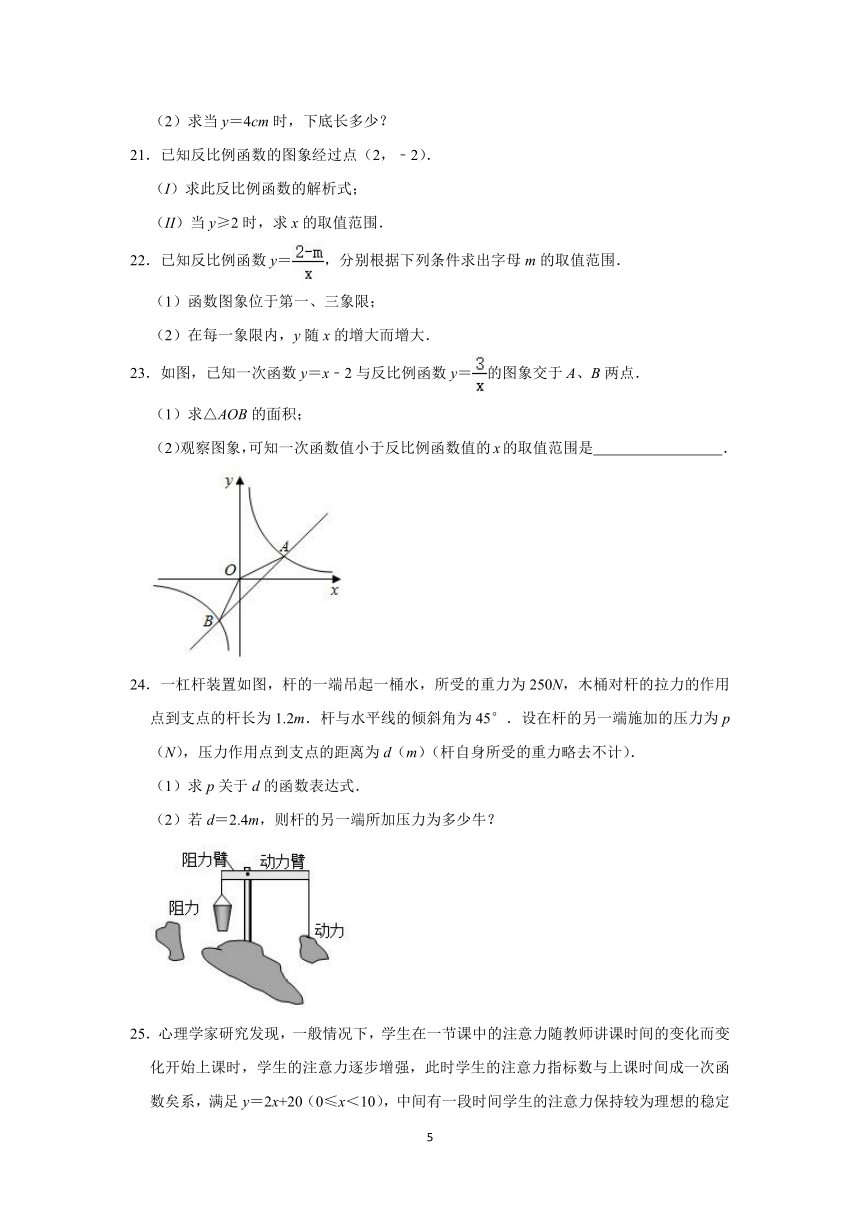
18.已知过原点O的直线与双曲线y=在一三象限分别交于A,B两点,点C在x轴上,且∠ACB=90°,tan∠ABC=,则△ABC的面积为 .
三.解答题(共8小题)
19.已知y=y1+y22,其中y1与x成正比例.y2与x成反比例.且当x=2和x=3时.y的值都为19,求y与变量x的函数关系式.
20.面积一定的梯形,其上底长是下底长的,设上底长为xcm,高为ycm,且当x=5cm,y=6cm,
(1)求y与x的函数关系式;
(2)求当y=4cm时,下底长多少?
21.已知反比例函数的图象经过点(2,﹣2).
(I)求此反比例函数的解析式;
(II)当y≥2时,求x的取值范围.
22.已知反比例函数y=,分别根据下列条件求出字母m的取值范围.
(1)函数图象位于第一、三象限;
(2)在每一象限内,y随x的增大而增大.
23.如图,已知一次函数y=x﹣2与反比例函数y=的图象交于A、B两点.
(1)求△AOB的面积;
(2)观察图象,可知一次函数值小于反比例函数值的x的取值范围是 .
24.一杠杆装置如图,杆的一端吊起一桶水,所受的重力为250N,木桶对杆的拉力的作用点到支点的杆长为1.2m.杆与水平线的倾斜角为45°.设在杆的另一端施加的压力为p(N),压力作用点到支点的距离为d(m)(杆自身所受的重力略去不计).
(1)求p关于d的函数表达式.
(2)若d=2.4m,则杆的另一端所加压力为多少牛?
25.心理学家研究发现,一般情况下,学生在一节课中的注意力随教师讲课时间的变化而变化开始上课时,学生的注意力逐步增强,此时学生的注意力指标数与上课时间成一次函数矣系,满足y=2x+20(0≤x<10),中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散,经过实验分析可知,学生的注意力指标数y随时间x(min)的变化规律如图所示(其中BC为水平线段,CD为双曲线的一部分).
(1)请根据图象,求出上课25min后学生的注意力指标数与上课时间所满足的函数表达式(不要求写出自变量的取值范围);
(2)一道数学作业题,需要讲22min,为了效果较好,老师能否经过适当安排,在学生注意力指标数不低于30的状态下讲完这道题目?请说明理由.
26.如图,四边形OABC是矩形,A、C分别在y轴、x轴上,且OA=6cm,OC=8cm,点P从点A开始以2cm/s的速度向B运动,点Q从点B开始以1cm/s的速度向C运动,设运动时间为t.
(1)如图(1),当t为何值时,△BPQ的面积为4cm2?
(2)当t为何值时,以B、P、Q为顶点的三角形与△ABC相似?
(3)如图(2),在运动过程中的某一时刻,反比例函数y=的图象恰好同时经过P、Q两点,求这个反比例函数的解析式.
湘教新版九年级上册《第1章 反比例函数》2023年单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:A、y=﹣不是反比例函数,选项A不符合题意;
B、y=是反比例函数,选项B符合题意;
C、y=1﹣不是反比例函数,选项C不符合题意;
D、y=x﹣6不是反比例函数,选项D不符合题意;
故选:B.
2.【解答】解:当a>0时,一次函数y=ax﹣2经过一、三、四象限,反比例y=函数在第一、三象限;
当a<0时,一次函数y=ax﹣2经过二、三、四象限,反比例y=函数在第二、四象限;
故选:C.
3.【解答】解:∵反比例函数y=,
∴该函数图象关于原点轴对称,故选项A正确;
在每个象限内,y随x的增大而减小,故选项B错误;
该函数图象为别位于第一、三象限,故选项C正确;
若点M(a,b)在其图象上,则ab=3,故选项D正确;
故选:B.
4.【解答】解:∵点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=﹣上,
∴(﹣2,y1),(﹣1,y2)分布在第二象限,(3,y3)在第四象限,每个象限内,y随x的增大而增大,
∴y3<y1<y2.
故选:D.
5.【解答】解:设A(a,b),B(c,d),
代入得:k1=ab,k2=cd,
∵S△AOB=4,
∴cd﹣ab=4,
∴cd﹣ab=8,
∴k2﹣k1=8,
故选:D.
6.【解答】解:∵点B在函数的图象上,点B的坐标是,
∴k=﹣2×2=﹣4,OA=4,
∴y=﹣,
作B1D⊥AA1,垂足为D,
∵△A1OA为等边三角形,
∴∠A1AB1=60°,
∴tan60°==,
∴B1D=AD,
设AD=a,
则OD=4+a,B1D=a,
∴B1(﹣4﹣a,a).
∵B1在反比例函数的图象上,
∴(﹣4﹣a) a=﹣4,
化简得a2+4a﹣4=0,
解得:a=﹣2±2.
∵a>0,
∴a=﹣2+2.
∴AA1=﹣4+4,
∴OA1=OA+AA1=4+(﹣4+4)=4,
∴点A1的坐标为(﹣4,0).
故选:D.
7.【解答】解:关于x的方程(x+1)2+(x﹣b)2=2化成一般形式是:2x2+(2﹣2b)x+(b2﹣1)=0,
∵关于x的方程(x+1)2+(x﹣b)2=2有两个相等的实数根,
∴Δ=(2﹣2b)2﹣8(b2﹣1)=﹣4(b+3)(b﹣1)=0,
解得:b=﹣3或1.
∵反比例函数的图象,在每个象限内y随x的增大而增大,
∴1+b<0
∴b<﹣1,
∴b=﹣3.
则反比例函数的解析式是:y=﹣.
故选:B.
8.【解答】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1500×0.4=FL,
则F=,
故选:C.
9.【解答】解:过A作AE⊥x轴于点E,
设A(a,b),B(x,b),
∵点A在反比例函数上,点B在反比例函数上,
∴ab=2,xb=4,
∴x=2a,
∴AB=2a﹣a=a,
∵四边形OABC是平行四边形,
∴CO=AB=a,
∴四边形OABC的面积是:CO AE=ab=2,
故选:C.
10.【解答】解:∵点A(m,﹣2m)在直线y1=﹣x+2上,
∴﹣2m=﹣m+2,
即m=﹣2,
∴点A(﹣2,4),
由两个函数的图以及交点坐标可知,
当x>﹣2时,y2>4或y2<0,
故选:D.
二.填空题(共8小题)
11.【解答】解:①x(y+1)不是函数,不符合题意;
②y=是y关于x+2的反比例函数,不符合题意;
③y=是y关于x2的反比例函数,不符合题意;
④y=﹣=,是y关于x的反比例函数,符合题意;
⑤y=是y关于x的正比例函数,不符合题意;
⑥y=x﹣1=,是y关于x的反比例函数,符合题意;
故答案为:④⑥.
12.【解答】解:过原点的一条直线即正比例函数的图象与反比例函数y=(k≠0)的图象分别交于A,B两点;
且两者都是中心对称图形;故A,B两点也关于原点对称;
若A点的坐标为(a,b),则B点的坐标为(﹣a,﹣b).
故答案为:(﹣a,﹣b).
13.【解答】解:一次函数y=kx+b(k≠0)的图象的形状是直线,反比例函数y=(k≠0)的图象的形状是双曲线.
故答案为:直线,双曲线.
14.【解答】解:把(﹣2,)代入y=中,得=,
解得k=﹣3,
所以反比例函数解析式为y=﹣.
故答案为:y=﹣.
15.【解答】解:解法1:(1)∵反比例函数y=(x>0)的图象经过点A(5,12),
∴k=12×5=60,
∴反比例函数的解析式为y=,
故答案为:y=;
(2)如图,连接AD并延长交x轴于E,
由A(5,12),可得AO==13,
∴BC=13,
∵AB∥CE,AB=BD,
∴∠CED=∠BAD=∠ADB=∠CDE,
∴CD=CE,
∴AB+CE=BD+CD=13,即OC+CE=13,
∴OE=13,
∴E(13,0),
由A(5,12),E(13,0),可得AE的解析式为y=﹣x+,
解方程组,可得,,
∴点D的坐标为(8,).
故答案为:(8,);
解法2:如图,过D作DH⊥x轴于H,过A作AG⊥x轴于G,
∵点A(5,12),
∴OG=5,AG=12,AO=13=BC,
∵∠AOG=∠DCH,∠AGO=∠DHC=90°,
∴△AOG∽△DCH,
∴可设CH=5k,DH=12k,CD=13k,
∴BD=13﹣13k,
∴OC=AB=13﹣13k,
∴OH=13﹣13k+5k=13﹣8k,
∴D(13﹣8k,12k),
∵反比例函数y=(x>0)的图象经过点A(5,12)和点D,
∴5×12=(13﹣8k)×12k,
解得k=,
∴D的坐标为(8,).
故答案为(8,).
16.【解答】解:∵点A(2,y1),B(3,y2)是反比例函数y=﹣图象上的两点,
∴y1=﹣=﹣6,y2=﹣=﹣4,
∴y1<y2.
故答案为<.
17.【解答】解:当y=6时,6=﹣,则x=﹣.
故答案为:﹣.
18.【解答】解:由题意可知OA=OB,
∵∠ACB=90°,OA=OB,
∵点C为x轴上一点,∠ACB=90°,
∴OA=OB=OC,
∴∠OCB=∠ABC,
∵∠OCB+∠ACD=∠CAD+∠ACD=90°,
∴∠CAD=∠ABC,
设点A为(,a),则OD=,AD=a,
∵tan∠ABC=,
∴tan∠CAD==,
∴CD=,
∴OA=OC=+a,
∵OA2=OD2+AD2,
∴(+a)2=()2+a2,
解得,a=2或﹣2(舍弃),
∴OC=,AD=2
∴S△ABC=2S△AOC=2×××2=5,
故答案为5.
三.解答题(共8小题)
19.【解答】解:∵y1与x成正比例.y2与x成反比例,
∴设y1=ax(a≠0),y2=(k≠0),
∴y=y1+y22=ax+,
∵当x=2和x=3时.y的值都为19,
∴代入得:,
解得:a=5,k2=36,
所以y与变量x的函数关系式是y=5x+.
20.【解答】解:(1)∵x=5cm,y=6cm,上底长是下底长的,
∴下底长为15cm,
∴梯形的面积=×(5+15)×6=60,
∴梯形的高=
∴y==;
(2)当y=4cm时,x=7.5,
∴3x=22.5.
答:下底长22.5cm.
21.【解答】解:(I)设解析式为y=,
把点(2,﹣2)代入解析式得,
﹣2=,
解得:k=﹣4
∴反比例函数的解析式y=﹣;
(II)当y=2时,x=﹣2,
如图,
所以当y≥2时,﹣2≤x<0.
22.【解答】解:(1)函数图象位于第一、三象限;根据反比例函数的性质,2﹣m>0,m<2;
(2)在每一象限内,y随x的增大而增大;根据反比例函数的性质,2﹣m<0,m>2.
23.【解答】解:(1)由解得或,
∴点A坐标(3,1),点B坐标(﹣1,﹣3),
设直线AB为y=kx+b,
由题意:解得,
∴直线AB为y=x﹣2,
∴与y轴交于点C(0,﹣2),
∴S△AOB=S△OCB+S△OCA=×2×1+×2×3=4;
(2)由图象可知:一次函数值小于反比例函数值的x的取值范围是0<x<3或x<﹣1,
故答案0<x<3或x<﹣1.
24.【解答】解:(1)由题意得,250×1.2=pd,
则p=.
(2)当d=2.4m时,p=125.
所以杆的另一端所施加的压力为125N.
25.【解答】解(1)设CD段所在双曲线的解析式为y=(k>0),
把C(25,40)代入上式得,,
∴k=1000,
∴上课25min后学生的注意力指标数与上课时间所满足的函数表达式为y=.
(2)对于AB段:y=2x+20(0≤x<10),
当y=30时,
2x+20=30,
∴x=5,
对于CD段:y=,
当y=30时,
=30,
∴x=,
∵﹣5=>22,
∴经过适当安排,老师能在学生注意力指标数不低于30的状态下讲完这道题目.
26.【解答】解:(1)由题意AB=OC=8cm,AO=BC=6cm,∠B=90°,
∵PA=2t,BQ=t,
∴PB=8﹣2t,
∵△BPQ的面积为4cm2,
∴ (8﹣2t) t=4,
解得t=2,
∴t=2s时,△PBQ的面积为4.
(2)①当△BPQ∽△BAC时,=,
∴=,
解得t=.
②当△BPQ∽△BCA时,=,
∴=,
解得t=,
∴t为s或s时,以B、P、Q为顶点的三角形与△ABC相似.
(3)由题意P(2t,6),Q(8,6﹣t),
∵反比例函数y=的图象恰好同时经过P、Q两点,
∴12t=8(6﹣t),
解得t=,
∴P(,6),
∴m=,
∴反比例函数的解析式为y=.
一.选择题(共10小题)
1.下列函数中,y是x的反比例函数的是( )
A. B. C. D.y=x﹣6
2.若a≠0,则一次函数y=ax﹣2与反比例y=函数在同一坐标系中的图象大致是( )
A. B.
C. D.
3.关于反比例函数y=,下列说法错误的是( )
A.图象关于原点对称
B.y随x的增大而减小
C.图象分别位于第一、三象限
D.若点M(a,b)在其图象上,则ab=3
4.若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=﹣上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2
5.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=4,则k2﹣k1的值是( )
A.1 B.2 C.4 D.8
6.如图,△OAB与△AA1B1都是等边三角形,点B,B1依次在函数的图象上,点A,A1依次在x轴的负半轴上,若点B的坐标是,则点A1的坐标是( )
A. B. C. D.
7.已知关于x的方程(x+1)2+(x﹣b)2=2有两个相等的实数根,且反比例函数的图象在每个象限内y随x的增大而增大,那么反比例函数的关系式为( )
A. B. C. D.
8.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,则动力F(单位:N)关于动力臂L(单位:m)的函数解析式正确的是( )
A.F= B.F= C.F= D.F=
9.如图,四边形OABC是平行四边形,点A在反比例函数上,点B在反比例函数上,点C在x轴的正半轴上,则四边形OABC的面积是( )
A.4 B.3 C.2 D.1
10.如图,直线y1=﹣x+2与双曲线y2=相交于A、B两点,已知点A坐标为(m,﹣2m),当x>m时,y2的取值范围为( )
A.y2>4 B.y2<4 C.0<y2<4 D.y2>4或y2<0
二.填空题(共8小题)
11.给出的六个关系式:①x(y+1);②y=;③y=;④y=﹣;⑤y=;⑥y=x﹣1,其中y是x的反比例函数是 .
12.如图,过原点的一条直线与反比例函数y=(k≠0)的图象分别交于A,B两点.若A点的坐标为(a,b),则B点的坐标为 .
13.一次函数y=kx+b(k≠0)的图象的形状是 ,反比例函数y=(k≠0)的图象的形状是 .
14.若反比例函数y=的图象经过点(﹣2,),则此函数的解析式为 .
15.如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=(x>0)图象经过点A(5,12),且与边BC交于点D.
(1)反比例函数y=的解析式为 ;
(2)若AB=BD,点D的坐标为 .
16.点A(2,y1),B(3,y2)是反比例函数y=﹣图象上的两点,那么y1,y2的大小关系是y1 y2.(填“>”,“<”或“=”)
17.已知反比例函数y=﹣,当y=6时,x= .
18.已知过原点O的直线与双曲线y=在一三象限分别交于A,B两点,点C在x轴上,且∠ACB=90°,tan∠ABC=,则△ABC的面积为 .
三.解答题(共8小题)
19.已知y=y1+y22,其中y1与x成正比例.y2与x成反比例.且当x=2和x=3时.y的值都为19,求y与变量x的函数关系式.
20.面积一定的梯形,其上底长是下底长的,设上底长为xcm,高为ycm,且当x=5cm,y=6cm,
(1)求y与x的函数关系式;
(2)求当y=4cm时,下底长多少?
21.已知反比例函数的图象经过点(2,﹣2).
(I)求此反比例函数的解析式;
(II)当y≥2时,求x的取值范围.
22.已知反比例函数y=,分别根据下列条件求出字母m的取值范围.
(1)函数图象位于第一、三象限;
(2)在每一象限内,y随x的增大而增大.
23.如图,已知一次函数y=x﹣2与反比例函数y=的图象交于A、B两点.
(1)求△AOB的面积;
(2)观察图象,可知一次函数值小于反比例函数值的x的取值范围是 .
24.一杠杆装置如图,杆的一端吊起一桶水,所受的重力为250N,木桶对杆的拉力的作用点到支点的杆长为1.2m.杆与水平线的倾斜角为45°.设在杆的另一端施加的压力为p(N),压力作用点到支点的距离为d(m)(杆自身所受的重力略去不计).
(1)求p关于d的函数表达式.
(2)若d=2.4m,则杆的另一端所加压力为多少牛?
25.心理学家研究发现,一般情况下,学生在一节课中的注意力随教师讲课时间的变化而变化开始上课时,学生的注意力逐步增强,此时学生的注意力指标数与上课时间成一次函数矣系,满足y=2x+20(0≤x<10),中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散,经过实验分析可知,学生的注意力指标数y随时间x(min)的变化规律如图所示(其中BC为水平线段,CD为双曲线的一部分).
(1)请根据图象,求出上课25min后学生的注意力指标数与上课时间所满足的函数表达式(不要求写出自变量的取值范围);
(2)一道数学作业题,需要讲22min,为了效果较好,老师能否经过适当安排,在学生注意力指标数不低于30的状态下讲完这道题目?请说明理由.
26.如图,四边形OABC是矩形,A、C分别在y轴、x轴上,且OA=6cm,OC=8cm,点P从点A开始以2cm/s的速度向B运动,点Q从点B开始以1cm/s的速度向C运动,设运动时间为t.
(1)如图(1),当t为何值时,△BPQ的面积为4cm2?
(2)当t为何值时,以B、P、Q为顶点的三角形与△ABC相似?
(3)如图(2),在运动过程中的某一时刻,反比例函数y=的图象恰好同时经过P、Q两点,求这个反比例函数的解析式.
湘教新版九年级上册《第1章 反比例函数》2023年单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:A、y=﹣不是反比例函数,选项A不符合题意;
B、y=是反比例函数,选项B符合题意;
C、y=1﹣不是反比例函数,选项C不符合题意;
D、y=x﹣6不是反比例函数,选项D不符合题意;
故选:B.
2.【解答】解:当a>0时,一次函数y=ax﹣2经过一、三、四象限,反比例y=函数在第一、三象限;
当a<0时,一次函数y=ax﹣2经过二、三、四象限,反比例y=函数在第二、四象限;
故选:C.
3.【解答】解:∵反比例函数y=,
∴该函数图象关于原点轴对称,故选项A正确;
在每个象限内,y随x的增大而减小,故选项B错误;
该函数图象为别位于第一、三象限,故选项C正确;
若点M(a,b)在其图象上,则ab=3,故选项D正确;
故选:B.
4.【解答】解:∵点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=﹣上,
∴(﹣2,y1),(﹣1,y2)分布在第二象限,(3,y3)在第四象限,每个象限内,y随x的增大而增大,
∴y3<y1<y2.
故选:D.
5.【解答】解:设A(a,b),B(c,d),
代入得:k1=ab,k2=cd,
∵S△AOB=4,
∴cd﹣ab=4,
∴cd﹣ab=8,
∴k2﹣k1=8,
故选:D.
6.【解答】解:∵点B在函数的图象上,点B的坐标是,
∴k=﹣2×2=﹣4,OA=4,
∴y=﹣,
作B1D⊥AA1,垂足为D,
∵△A1OA为等边三角形,
∴∠A1AB1=60°,
∴tan60°==,
∴B1D=AD,
设AD=a,
则OD=4+a,B1D=a,
∴B1(﹣4﹣a,a).
∵B1在反比例函数的图象上,
∴(﹣4﹣a) a=﹣4,
化简得a2+4a﹣4=0,
解得:a=﹣2±2.
∵a>0,
∴a=﹣2+2.
∴AA1=﹣4+4,
∴OA1=OA+AA1=4+(﹣4+4)=4,
∴点A1的坐标为(﹣4,0).
故选:D.
7.【解答】解:关于x的方程(x+1)2+(x﹣b)2=2化成一般形式是:2x2+(2﹣2b)x+(b2﹣1)=0,
∵关于x的方程(x+1)2+(x﹣b)2=2有两个相等的实数根,
∴Δ=(2﹣2b)2﹣8(b2﹣1)=﹣4(b+3)(b﹣1)=0,
解得:b=﹣3或1.
∵反比例函数的图象,在每个象限内y随x的增大而增大,
∴1+b<0
∴b<﹣1,
∴b=﹣3.
则反比例函数的解析式是:y=﹣.
故选:B.
8.【解答】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1500×0.4=FL,
则F=,
故选:C.
9.【解答】解:过A作AE⊥x轴于点E,
设A(a,b),B(x,b),
∵点A在反比例函数上,点B在反比例函数上,
∴ab=2,xb=4,
∴x=2a,
∴AB=2a﹣a=a,
∵四边形OABC是平行四边形,
∴CO=AB=a,
∴四边形OABC的面积是:CO AE=ab=2,
故选:C.
10.【解答】解:∵点A(m,﹣2m)在直线y1=﹣x+2上,
∴﹣2m=﹣m+2,
即m=﹣2,
∴点A(﹣2,4),
由两个函数的图以及交点坐标可知,
当x>﹣2时,y2>4或y2<0,
故选:D.
二.填空题(共8小题)
11.【解答】解:①x(y+1)不是函数,不符合题意;
②y=是y关于x+2的反比例函数,不符合题意;
③y=是y关于x2的反比例函数,不符合题意;
④y=﹣=,是y关于x的反比例函数,符合题意;
⑤y=是y关于x的正比例函数,不符合题意;
⑥y=x﹣1=,是y关于x的反比例函数,符合题意;
故答案为:④⑥.
12.【解答】解:过原点的一条直线即正比例函数的图象与反比例函数y=(k≠0)的图象分别交于A,B两点;
且两者都是中心对称图形;故A,B两点也关于原点对称;
若A点的坐标为(a,b),则B点的坐标为(﹣a,﹣b).
故答案为:(﹣a,﹣b).
13.【解答】解:一次函数y=kx+b(k≠0)的图象的形状是直线,反比例函数y=(k≠0)的图象的形状是双曲线.
故答案为:直线,双曲线.
14.【解答】解:把(﹣2,)代入y=中,得=,
解得k=﹣3,
所以反比例函数解析式为y=﹣.
故答案为:y=﹣.
15.【解答】解:解法1:(1)∵反比例函数y=(x>0)的图象经过点A(5,12),
∴k=12×5=60,
∴反比例函数的解析式为y=,
故答案为:y=;
(2)如图,连接AD并延长交x轴于E,
由A(5,12),可得AO==13,
∴BC=13,
∵AB∥CE,AB=BD,
∴∠CED=∠BAD=∠ADB=∠CDE,
∴CD=CE,
∴AB+CE=BD+CD=13,即OC+CE=13,
∴OE=13,
∴E(13,0),
由A(5,12),E(13,0),可得AE的解析式为y=﹣x+,
解方程组,可得,,
∴点D的坐标为(8,).
故答案为:(8,);
解法2:如图,过D作DH⊥x轴于H,过A作AG⊥x轴于G,
∵点A(5,12),
∴OG=5,AG=12,AO=13=BC,
∵∠AOG=∠DCH,∠AGO=∠DHC=90°,
∴△AOG∽△DCH,
∴可设CH=5k,DH=12k,CD=13k,
∴BD=13﹣13k,
∴OC=AB=13﹣13k,
∴OH=13﹣13k+5k=13﹣8k,
∴D(13﹣8k,12k),
∵反比例函数y=(x>0)的图象经过点A(5,12)和点D,
∴5×12=(13﹣8k)×12k,
解得k=,
∴D的坐标为(8,).
故答案为(8,).
16.【解答】解:∵点A(2,y1),B(3,y2)是反比例函数y=﹣图象上的两点,
∴y1=﹣=﹣6,y2=﹣=﹣4,
∴y1<y2.
故答案为<.
17.【解答】解:当y=6时,6=﹣,则x=﹣.
故答案为:﹣.
18.【解答】解:由题意可知OA=OB,
∵∠ACB=90°,OA=OB,
∵点C为x轴上一点,∠ACB=90°,
∴OA=OB=OC,
∴∠OCB=∠ABC,
∵∠OCB+∠ACD=∠CAD+∠ACD=90°,
∴∠CAD=∠ABC,
设点A为(,a),则OD=,AD=a,
∵tan∠ABC=,
∴tan∠CAD==,
∴CD=,
∴OA=OC=+a,
∵OA2=OD2+AD2,
∴(+a)2=()2+a2,
解得,a=2或﹣2(舍弃),
∴OC=,AD=2
∴S△ABC=2S△AOC=2×××2=5,
故答案为5.
三.解答题(共8小题)
19.【解答】解:∵y1与x成正比例.y2与x成反比例,
∴设y1=ax(a≠0),y2=(k≠0),
∴y=y1+y22=ax+,
∵当x=2和x=3时.y的值都为19,
∴代入得:,
解得:a=5,k2=36,
所以y与变量x的函数关系式是y=5x+.
20.【解答】解:(1)∵x=5cm,y=6cm,上底长是下底长的,
∴下底长为15cm,
∴梯形的面积=×(5+15)×6=60,
∴梯形的高=
∴y==;
(2)当y=4cm时,x=7.5,
∴3x=22.5.
答:下底长22.5cm.
21.【解答】解:(I)设解析式为y=,
把点(2,﹣2)代入解析式得,
﹣2=,
解得:k=﹣4
∴反比例函数的解析式y=﹣;
(II)当y=2时,x=﹣2,
如图,
所以当y≥2时,﹣2≤x<0.
22.【解答】解:(1)函数图象位于第一、三象限;根据反比例函数的性质,2﹣m>0,m<2;
(2)在每一象限内,y随x的增大而增大;根据反比例函数的性质,2﹣m<0,m>2.
23.【解答】解:(1)由解得或,
∴点A坐标(3,1),点B坐标(﹣1,﹣3),
设直线AB为y=kx+b,
由题意:解得,
∴直线AB为y=x﹣2,
∴与y轴交于点C(0,﹣2),
∴S△AOB=S△OCB+S△OCA=×2×1+×2×3=4;
(2)由图象可知:一次函数值小于反比例函数值的x的取值范围是0<x<3或x<﹣1,
故答案0<x<3或x<﹣1.
24.【解答】解:(1)由题意得,250×1.2=pd,
则p=.
(2)当d=2.4m时,p=125.
所以杆的另一端所施加的压力为125N.
25.【解答】解(1)设CD段所在双曲线的解析式为y=(k>0),
把C(25,40)代入上式得,,
∴k=1000,
∴上课25min后学生的注意力指标数与上课时间所满足的函数表达式为y=.
(2)对于AB段:y=2x+20(0≤x<10),
当y=30时,
2x+20=30,
∴x=5,
对于CD段:y=,
当y=30时,
=30,
∴x=,
∵﹣5=>22,
∴经过适当安排,老师能在学生注意力指标数不低于30的状态下讲完这道题目.
26.【解答】解:(1)由题意AB=OC=8cm,AO=BC=6cm,∠B=90°,
∵PA=2t,BQ=t,
∴PB=8﹣2t,
∵△BPQ的面积为4cm2,
∴ (8﹣2t) t=4,
解得t=2,
∴t=2s时,△PBQ的面积为4.
(2)①当△BPQ∽△BAC时,=,
∴=,
解得t=.
②当△BPQ∽△BCA时,=,
∴=,
解得t=,
∴t为s或s时,以B、P、Q为顶点的三角形与△ABC相似.
(3)由题意P(2t,6),Q(8,6﹣t),
∵反比例函数y=的图象恰好同时经过P、Q两点,
∴12t=8(6﹣t),
解得t=,
∴P(,6),
∴m=,
∴反比例函数的解析式为y=.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
