三角形全等的条件(河北省唐山市)
文档属性
| 名称 | 三角形全等的条件(河北省唐山市) |
|
|
| 格式 | rar | ||
| 文件大小 | 29.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-21 00:00:00 | ||
图片预览

文档简介
三角形全等的条件
学习目标:
1.掌握“斜边、直角边”条件的内容.
2.初步运用“斜边、直角边”条件证明两个直角三角形全等.
一、知识回顾
1.问题:(1)判定一般三角形全等的方法有哪几种? 、 、 、 。
(2)若这两个三角形是直角三角形,那么这些判定方法适用吗? 。
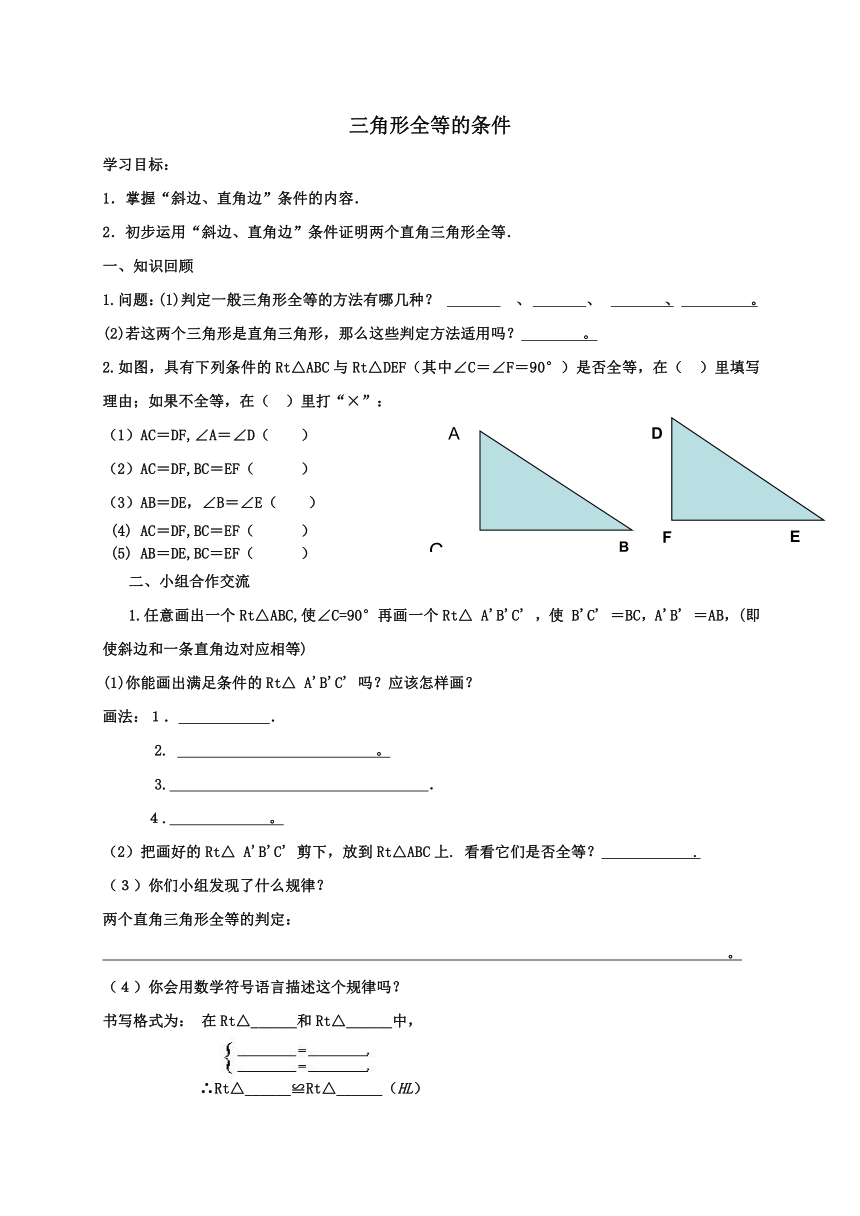
2.如图,具有下列条件的Rt△ABC与Rt△DEF(其中∠C=∠F=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=DF,∠A=∠D( )
(2)AC=DF,BC=EF( )
(3)AB=DE,∠B=∠E( )
(4) AC=DF,BC=EF( )
(5) AB=DE,BC=EF( )
二、小组合作交流
1.任意画出一个Rt△ABC,使∠C=90°再画一个Rt△ A'B'C' ,使 B'C' =BC,A'B' =AB,(即使斜边和一条直角边对应相等)
(1)你能画出满足条件的Rt△ A'B'C' 吗?应该怎样画?
画法:1. .
2. 。
3. .
4. 。
(2)把画好的Rt△ A'B'C' 剪下,放到Rt△ABC上. 看看它们是否全等? .
(3)你们小组发现了什么规律?
两个直角三角形全等的判定:
。
(4)你会用数学符号语言描述这个规律吗?
书写格式为: 在Rt△______和Rt△______中,
∴Rt△______≌Rt△______(HL)
注意“HL”是仅适用于Rt△的特殊方法。应用HL判定时,虽只有两个条件,但必须先有两个Rt△。
(5)你能把证明直角三角形全等的方法列举出来吗?
、 、 、 、 。
三 、小试牛刀
1.如图:AC⊥BC,BD⊥AD,AC=BD.
(1)求证:BC=AD.
(2)你还能找到其他的全等三角形吗?
(3)你可以得到哪些线段相等?
四、跳一跳摘桃子
如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.DA ⊥AB,EB ⊥AB,D,E与路段AB的距离相等吗?为什么?
五、走进中考
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。
F
E
D
B
C
A
学习目标:
1.掌握“斜边、直角边”条件的内容.
2.初步运用“斜边、直角边”条件证明两个直角三角形全等.
一、知识回顾
1.问题:(1)判定一般三角形全等的方法有哪几种? 、 、 、 。
(2)若这两个三角形是直角三角形,那么这些判定方法适用吗? 。
2.如图,具有下列条件的Rt△ABC与Rt△DEF(其中∠C=∠F=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=DF,∠A=∠D( )
(2)AC=DF,BC=EF( )
(3)AB=DE,∠B=∠E( )
(4) AC=DF,BC=EF( )
(5) AB=DE,BC=EF( )
二、小组合作交流
1.任意画出一个Rt△ABC,使∠C=90°再画一个Rt△ A'B'C' ,使 B'C' =BC,A'B' =AB,(即使斜边和一条直角边对应相等)
(1)你能画出满足条件的Rt△ A'B'C' 吗?应该怎样画?
画法:1. .
2. 。
3. .
4. 。
(2)把画好的Rt△ A'B'C' 剪下,放到Rt△ABC上. 看看它们是否全等? .
(3)你们小组发现了什么规律?
两个直角三角形全等的判定:
。
(4)你会用数学符号语言描述这个规律吗?
书写格式为: 在Rt△______和Rt△______中,
∴Rt△______≌Rt△______(HL)
注意“HL”是仅适用于Rt△的特殊方法。应用HL判定时,虽只有两个条件,但必须先有两个Rt△。
(5)你能把证明直角三角形全等的方法列举出来吗?
、 、 、 、 。
三 、小试牛刀
1.如图:AC⊥BC,BD⊥AD,AC=BD.
(1)求证:BC=AD.
(2)你还能找到其他的全等三角形吗?
(3)你可以得到哪些线段相等?
四、跳一跳摘桃子
如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.DA ⊥AB,EB ⊥AB,D,E与路段AB的距离相等吗?为什么?
五、走进中考
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。
F
E
D
B
C
A
