2014-2023年高考数学真题专题分类--2.5 函数的图象(含解析)
文档属性
| 名称 | 2014-2023年高考数学真题专题分类--2.5 函数的图象(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 16:57:52 | ||
图片预览


文档简介
2014-2023年高考数学真题专题分类
2.5 函数的图象
考点 函数的图象
1.(2017课标Ⅰ文,8,5分)函数y=的部分图象大致为( )
答案 C 本题考查函数图象的识辨.
易知y=为奇函数,图象关于原点对称,故排除B选项;sin2≈sin120°=,cos1≈cos60°=,
则f(1)==,故排除A选项;
f(π)==0,故排除D选项,故选C.
方法总结 已知函数解析式判断函数图象的方法:
(1)根据函数的定义域判断图象的左右位置,根据函数的值域判断图象的上下位置;
(2)根据函数的单调性判断图象的变化趋势;
(3)根据函数的奇偶性判断图象的对称性;
(4)根据函数的周期性判断图象的循环往复.
2.(2017课标Ⅲ文,7,5分)函数y=1+x+的部分图象大致为( )
答案 D 当x∈(0,1)时,sinx>0,
∴y=1+x+>1+x>1,排除A、C.
令f(x)=x+,则f(-x)=-x+=-f(x),
∴f(x)=x+是奇函数,
∴y=1+x+的图象关于点(0,1)对称,故排除B.
故选D.
解后反思 函数图象问题,一般从定义域、特殊点的函数值、单调性、奇偶性等方面入手进行分析.选择题通常采用排除法.
3.(2017天津文,8,5分)已知函数f(x)=设a∈R,若关于x的不等式f(x)≥在R上恒成立,则a的取值范围是( )
A.[-2,2] B.[-2,2]
C.[-2,2] D.[-2,2]
答案 A 令g(x)=,
当a≤0时,如图1所示,
若f(x)≥g(x)恒成立,则g(0)≤2,得a≥-2,
∴-2≤a≤0;
图1
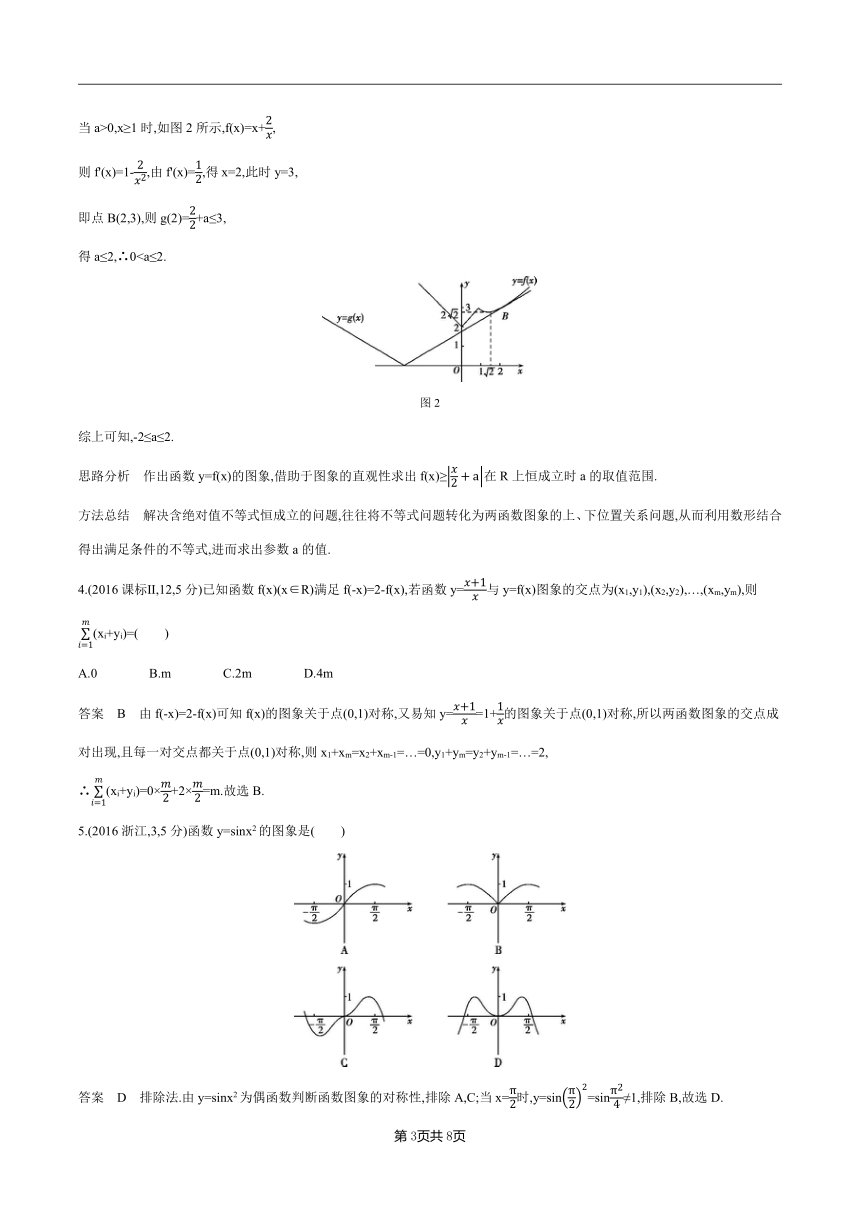
当a>0,x≥1时,如图2所示,f(x)=x+,
则f'(x)=1-,由f'(x)=,得x=2,此时y=3,
即点B(2,3),则g(2)=+a≤3,
得a≤2,∴0图2
综上可知,-2≤a≤2.
思路分析 作出函数y=f(x)的图象,借助于图象的直观性求出f(x)≥在R上恒成立时a的取值范围.
方法总结 解决含绝对值不等式恒成立的问题,往往将不等式问题转化为两函数图象的上、下位置关系问题,从而利用数形结合得出满足条件的不等式,进而求出参数a的值.
4.(2016课标Ⅱ,12,5分)已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则(xi+yi)=( )
A.0 B.m C.2m D.4m
答案 B 由f(-x)=2-f(x)可知f(x)的图象关于点(0,1)对称,又易知y==1+的图象关于点(0,1)对称,所以两函数图象的交点成对出现,且每一对交点都关于点(0,1)对称,则x1+xm=x2+xm-1=…=0,y1+ym=y2+ym-1=…=2,
∴(xi+yi)=0×+2×=m.故选B.
5.(2016浙江,3,5分)函数y=sinx2的图象是( )
答案 D 排除法.由y=sinx2为偶函数判断函数图象的对称性,排除A,C;当x=时,y=sin=sin≠1,排除B,故选D.
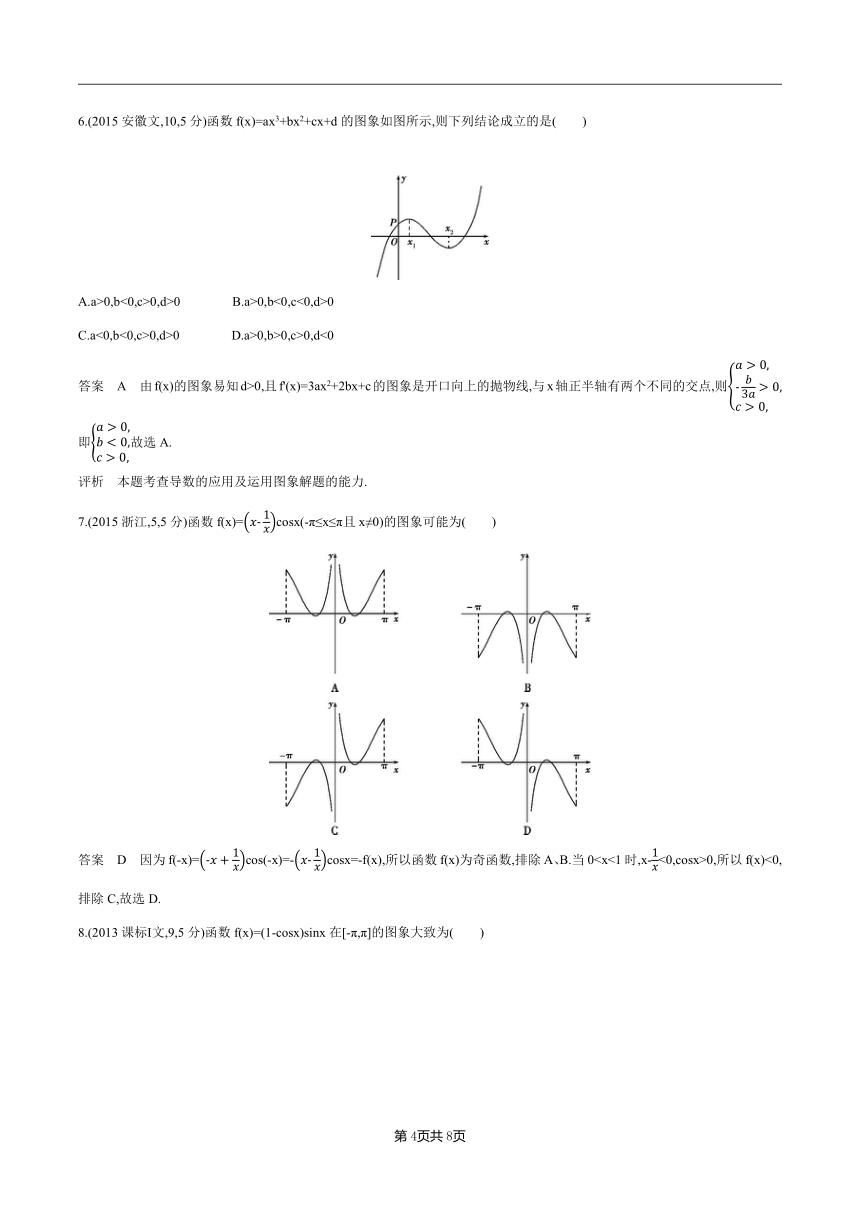
6.(2015安徽文,10,5分)函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是( )
A.a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0
C.a<0,b<0,c>0,d>0 D.a>0,b>0,c>0,d<0
答案 A 由f(x)的图象易知d>0,且f'(x)=3ax2+2bx+c的图象是开口向上的抛物线,与x轴正半轴有两个不同的交点,则即故选A.
评析 本题考查导数的应用及运用图象解题的能力.
7.(2015浙江,5,5分)函数f(x)=cosx(-π≤x≤π且x≠0)的图象可能为( )
答案 D 因为f(-x)=cos(-x)=-cosx=-f(x),所以函数f(x)为奇函数,排除A、B.当00,所以f(x)<0,排除C,故选D.
8.(2013课标Ⅰ文,9,5分)函数f(x)=(1-cosx)sinx在[-π,π]的图象大致为( )
答案 C 因为f(-x)=[1-cos(-x)]sin(-x)=-(1-cosx)·sinx=-f(x),所以函数f(x)为奇函数,图象关于原点对称,排除选项B;当x∈(0,π)时,1-cosx>0,sinx>0,所以f(x)>0,排除选项A;又函数f(x)的导函数f'(x)=sinx·sinx+(1-cosx)·cosx,所以f'(0)=0,排除D.故选C.
评析 本题考查对函数图象的识辨能力,考查综合运用所学知识的意识,体现了数形结合的思想方法;难点是判断选项C中f'(0)=0.
9.(2012课标理,10,5分)已知函数f(x)=,则y=f(x)的图象大致为( )
答案 B 令g(x)=ln(x+1)-x,则g'(x)=-1=,
∴当-10,
当x>0时,g'(x)<0,∴g(x)max=g(0)=0.
∴f(x)<0,排除A、C,又由定义域可排除D,故选B.
评析 本题考查了函数的图象,考查了利用导数判断函数单调性,求值域,考查了数形结合的数学思想.
10.(2013北京理,5,5分)函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)=( )
A.ex+1 B.ex-1 C.e-x+1 D.e-x-1
答案 D 与曲线y=ex关于y轴对称的图象对应的函数为y=e-x,将函数y=e-x的图象向左平移1个单位长度即得y=f(x)的图象,∴f(x)=e-(x+1)=e-x-1,故选D.
11.(2012湖北文,6,5分)已知定义在区间[0,2]上的函数y=f(x)的图象如图所示,则y=-f(2-x)的图象为( )
答案 B 当x=1时,y=-f(1)=-1,排除A、C.
当x=2时,y=-f(0)=0,故选B.
评析 结合选项,利用特殊值求解.
12.(2022全国甲,理5,文7,5分)函数y=(3x-3-x)cos x在区间的图象大致为( )
答案 A 设f(x)=(3x-3-x)cos x.
∵f(-x)=(3-x-3x)cos(-x)=-f(x),且区间关于原点对称,
∴f(x)为奇函数,故排除B,D.
又f(1)=cos 1>0,故排除C.故选A.
13.(2022全国乙文,8,5分)下图是下列四个函数中的某个函数在区间[-3,3]的大致图象,则该函数是 ( )
A.y=
B.y=
C.y=
D.y=
答案 A 由题图可知,当x=3时,y<0.
对于B,当x=3时,y=>0,故排除B.
对于D,∵<3<π,∴sin 3>0,∴当x=3时,y=>0,故排除D.
对于C,当0∴≤cos x<1,由题图可知当014.(2021浙江,7,4分)已知函数f(x)=x2+,g(x)=sin x,则图象为右图的函数可能是( )
A.y=f(x)+g(x)- B.y=f(x)-g(x)-
C.y=f(x)g(x) D.y=
答案 D 解题指导:由f(x)=x2+,g(x)=sin x,结合题设所给函数图象知,其所对应的函数具有以下特性:①奇函数,②在上先增后减.利用排除法得出答案.
解析 由题图可知函数为奇函数且在上先增后减.A选项,y=x2+sin x,B选项,y=x2-sin x均不符合奇函数这条性质,故排除;C选项,y=·sin x,显然f(x),g(x)均在上单调递增,且f(x)>0,g(x)>0,故y=sin x在上单调递增,故排除.故选D.
方法总结:函数图象的识辨问题,一般从以下几个方面进行分析:①定义域,②奇偶性、单调性,③特殊点,④函数值的正负,⑤极限,利用排除法快速选出答案.
15.(2023天津,4,5分,易)函数f(x)的图象如图所示,则f(x)的解析式可能为 ( )
A.f(x)= B.f(x)=
C.f(x)= D.f(x)=
答案 D 由题图可知f(x)为偶函数,而选项A,B中的函数均为奇函数,所以排除A,B.又因为选项C中, f(x)=>0恒成立,故排除C,故选D.
16.(2016山东,15,5分)已知函数f(x)=其中m>0.若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 .
答案 (3,+∞)
解析 f(x)的图象如图所示,
若存在实数b,使得关于x的方程f(x)=b有三个不同的根,只需4m-m23或m<0,又m>0,所以m>3.
方法总结 分段函数问题、函数零点个数问题或方程根的个数问题通常采用数形结合的思想方法来解决.
17.(2015安徽文,14,5分)在平面直角坐标系xOy中,若直线y=2a与函数y=|x-a|-1的图象只有一个交点,则a的值为 .
答案 -
解析 若直线y=2a与函数y=|x-a|-1的图象只有一个交点,则方程2a=|x-a|-1只有一解,即方程|x-a|=2a+1只有一解,故2a+1=0,所以a=-.
(
第
1
页共
7
页
)
2.5 函数的图象
考点 函数的图象
1.(2017课标Ⅰ文,8,5分)函数y=的部分图象大致为( )
答案 C 本题考查函数图象的识辨.
易知y=为奇函数,图象关于原点对称,故排除B选项;sin2≈sin120°=,cos1≈cos60°=,
则f(1)==,故排除A选项;
f(π)==0,故排除D选项,故选C.
方法总结 已知函数解析式判断函数图象的方法:
(1)根据函数的定义域判断图象的左右位置,根据函数的值域判断图象的上下位置;
(2)根据函数的单调性判断图象的变化趋势;
(3)根据函数的奇偶性判断图象的对称性;
(4)根据函数的周期性判断图象的循环往复.
2.(2017课标Ⅲ文,7,5分)函数y=1+x+的部分图象大致为( )
答案 D 当x∈(0,1)时,sinx>0,
∴y=1+x+>1+x>1,排除A、C.
令f(x)=x+,则f(-x)=-x+=-f(x),
∴f(x)=x+是奇函数,
∴y=1+x+的图象关于点(0,1)对称,故排除B.
故选D.
解后反思 函数图象问题,一般从定义域、特殊点的函数值、单调性、奇偶性等方面入手进行分析.选择题通常采用排除法.
3.(2017天津文,8,5分)已知函数f(x)=设a∈R,若关于x的不等式f(x)≥在R上恒成立,则a的取值范围是( )
A.[-2,2] B.[-2,2]
C.[-2,2] D.[-2,2]
答案 A 令g(x)=,
当a≤0时,如图1所示,
若f(x)≥g(x)恒成立,则g(0)≤2,得a≥-2,
∴-2≤a≤0;
图1
当a>0,x≥1时,如图2所示,f(x)=x+,
则f'(x)=1-,由f'(x)=,得x=2,此时y=3,
即点B(2,3),则g(2)=+a≤3,
得a≤2,∴0
综上可知,-2≤a≤2.
思路分析 作出函数y=f(x)的图象,借助于图象的直观性求出f(x)≥在R上恒成立时a的取值范围.
方法总结 解决含绝对值不等式恒成立的问题,往往将不等式问题转化为两函数图象的上、下位置关系问题,从而利用数形结合得出满足条件的不等式,进而求出参数a的值.
4.(2016课标Ⅱ,12,5分)已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则(xi+yi)=( )
A.0 B.m C.2m D.4m
答案 B 由f(-x)=2-f(x)可知f(x)的图象关于点(0,1)对称,又易知y==1+的图象关于点(0,1)对称,所以两函数图象的交点成对出现,且每一对交点都关于点(0,1)对称,则x1+xm=x2+xm-1=…=0,y1+ym=y2+ym-1=…=2,
∴(xi+yi)=0×+2×=m.故选B.
5.(2016浙江,3,5分)函数y=sinx2的图象是( )
答案 D 排除法.由y=sinx2为偶函数判断函数图象的对称性,排除A,C;当x=时,y=sin=sin≠1,排除B,故选D.
6.(2015安徽文,10,5分)函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是( )
A.a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0
C.a<0,b<0,c>0,d>0 D.a>0,b>0,c>0,d<0
答案 A 由f(x)的图象易知d>0,且f'(x)=3ax2+2bx+c的图象是开口向上的抛物线,与x轴正半轴有两个不同的交点,则即故选A.
评析 本题考查导数的应用及运用图象解题的能力.
7.(2015浙江,5,5分)函数f(x)=cosx(-π≤x≤π且x≠0)的图象可能为( )
答案 D 因为f(-x)=cos(-x)=-cosx=-f(x),所以函数f(x)为奇函数,排除A、B.当0
8.(2013课标Ⅰ文,9,5分)函数f(x)=(1-cosx)sinx在[-π,π]的图象大致为( )
答案 C 因为f(-x)=[1-cos(-x)]sin(-x)=-(1-cosx)·sinx=-f(x),所以函数f(x)为奇函数,图象关于原点对称,排除选项B;当x∈(0,π)时,1-cosx>0,sinx>0,所以f(x)>0,排除选项A;又函数f(x)的导函数f'(x)=sinx·sinx+(1-cosx)·cosx,所以f'(0)=0,排除D.故选C.
评析 本题考查对函数图象的识辨能力,考查综合运用所学知识的意识,体现了数形结合的思想方法;难点是判断选项C中f'(0)=0.
9.(2012课标理,10,5分)已知函数f(x)=,则y=f(x)的图象大致为( )
答案 B 令g(x)=ln(x+1)-x,则g'(x)=-1=,
∴当-1
当x>0时,g'(x)<0,∴g(x)max=g(0)=0.
∴f(x)<0,排除A、C,又由定义域可排除D,故选B.
评析 本题考查了函数的图象,考查了利用导数判断函数单调性,求值域,考查了数形结合的数学思想.
10.(2013北京理,5,5分)函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)=( )
A.ex+1 B.ex-1 C.e-x+1 D.e-x-1
答案 D 与曲线y=ex关于y轴对称的图象对应的函数为y=e-x,将函数y=e-x的图象向左平移1个单位长度即得y=f(x)的图象,∴f(x)=e-(x+1)=e-x-1,故选D.
11.(2012湖北文,6,5分)已知定义在区间[0,2]上的函数y=f(x)的图象如图所示,则y=-f(2-x)的图象为( )
答案 B 当x=1时,y=-f(1)=-1,排除A、C.
当x=2时,y=-f(0)=0,故选B.
评析 结合选项,利用特殊值求解.
12.(2022全国甲,理5,文7,5分)函数y=(3x-3-x)cos x在区间的图象大致为( )
答案 A 设f(x)=(3x-3-x)cos x.
∵f(-x)=(3-x-3x)cos(-x)=-f(x),且区间关于原点对称,
∴f(x)为奇函数,故排除B,D.
又f(1)=cos 1>0,故排除C.故选A.
13.(2022全国乙文,8,5分)下图是下列四个函数中的某个函数在区间[-3,3]的大致图象,则该函数是 ( )
A.y=
B.y=
C.y=
D.y=
答案 A 由题图可知,当x=3时,y<0.
对于B,当x=3时,y=>0,故排除B.
对于D,∵<3<π,∴sin 3>0,∴当x=3时,y=>0,故排除D.
对于C,当0
A.y=f(x)+g(x)- B.y=f(x)-g(x)-
C.y=f(x)g(x) D.y=
答案 D 解题指导:由f(x)=x2+,g(x)=sin x,结合题设所给函数图象知,其所对应的函数具有以下特性:①奇函数,②在上先增后减.利用排除法得出答案.
解析 由题图可知函数为奇函数且在上先增后减.A选项,y=x2+sin x,B选项,y=x2-sin x均不符合奇函数这条性质,故排除;C选项,y=·sin x,显然f(x),g(x)均在上单调递增,且f(x)>0,g(x)>0,故y=sin x在上单调递增,故排除.故选D.
方法总结:函数图象的识辨问题,一般从以下几个方面进行分析:①定义域,②奇偶性、单调性,③特殊点,④函数值的正负,⑤极限,利用排除法快速选出答案.
15.(2023天津,4,5分,易)函数f(x)的图象如图所示,则f(x)的解析式可能为 ( )
A.f(x)= B.f(x)=
C.f(x)= D.f(x)=
答案 D 由题图可知f(x)为偶函数,而选项A,B中的函数均为奇函数,所以排除A,B.又因为选项C中, f(x)=>0恒成立,故排除C,故选D.
16.(2016山东,15,5分)已知函数f(x)=其中m>0.若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 .
答案 (3,+∞)
解析 f(x)的图象如图所示,
若存在实数b,使得关于x的方程f(x)=b有三个不同的根,只需4m-m2
方法总结 分段函数问题、函数零点个数问题或方程根的个数问题通常采用数形结合的思想方法来解决.
17.(2015安徽文,14,5分)在平面直角坐标系xOy中,若直线y=2a与函数y=|x-a|-1的图象只有一个交点,则a的值为 .
答案 -
解析 若直线y=2a与函数y=|x-a|-1的图象只有一个交点,则方程2a=|x-a|-1只有一解,即方程|x-a|=2a+1只有一解,故2a+1=0,所以a=-.
(
第
1
页共
7
页
)
同课章节目录
