2014-2023年高考数学真题专题分类--6.2 等差数列(含解析)
文档属性
| 名称 | 2014-2023年高考数学真题专题分类--6.2 等差数列(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 305.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 17:09:42 | ||
图片预览




文档简介
2014-2023年高考数学真题专题分类
6.2 等差数列
考点一 等差数列及其前n项和
1.(2016课标Ⅰ,3,5分)已知等差数列{an}前9项的和为27,a10=8,则a100=( )
A.100 B.99 C.98 D.97
答案 C 设{an}的公差为d,由等差数列前n项和公式及通项公式,得解得∴an=a1+(n-1)·d=n-2,∴a100=100-2=98.故选C.
方法总结 已知条件中有具体的an、Sn的值时,通常用基本量法处理,即在a1、d、n、an、Sn这5个量中知三求二.
一题多解 由S9=·9=·9=9a5=27,可得a5=3,
所以a10-a5=5d=5,所以d=1,
所以a100=a10+90d=98.故选C.
2.(2015课标Ⅰ文,7,5分)已知{an}是公差为1的等差数列,Sn为{an}的前n项和.若S8=4S4,则a10=( )
A. B. C.10 D.12
答案 B 由S8=4S4得8a1+×1=4×,解得a1=,∴a10=a1+9d=,故选B.
评析 本题主要考查等差数列的前n项和,计算准确是解题关键,属容易题.
3.(2015浙江理,3,5分)已知{an}是等差数列,公差d不为零,前n项和是Sn.若a3,a4,a8成等比数列,则( )
A.a1d>0,dS4>0 B.a1d<0,dS4<0
C.a1d>0,dS4<0 D.a1d<0,dS4>0
答案 B 由=a3a8,得(a1+2d)(a1+7d)=(a1+3d)2,整理得d(5d+3a1)=0,又d≠0,∴a1=-d,则a1d=-d2<0,又∵S4=4a1+6d=-d,∴dS4=-d2<0,故选B.
4.(2013课标Ⅰ理,7,5分)设等差数列{an}的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m=( )
A.3 B.4 C.5 D.6
答案 C 解法一:∵Sm-1=-2,Sm=0,Sm+1=3,∴am=Sm-Sm-1=2,am+1=Sm+1-Sm=3,∴公差d=am+1-am=1,由Sn=na1+d=na1+,
得
由①得a1=,代入②可得m=5.
解法二:∵数列{an}为等差数列,且前n项和为Sn,
∴数列也为等差数列.
∴+=,即+=0,解得m=5.经检验为原方程的解.故选C.
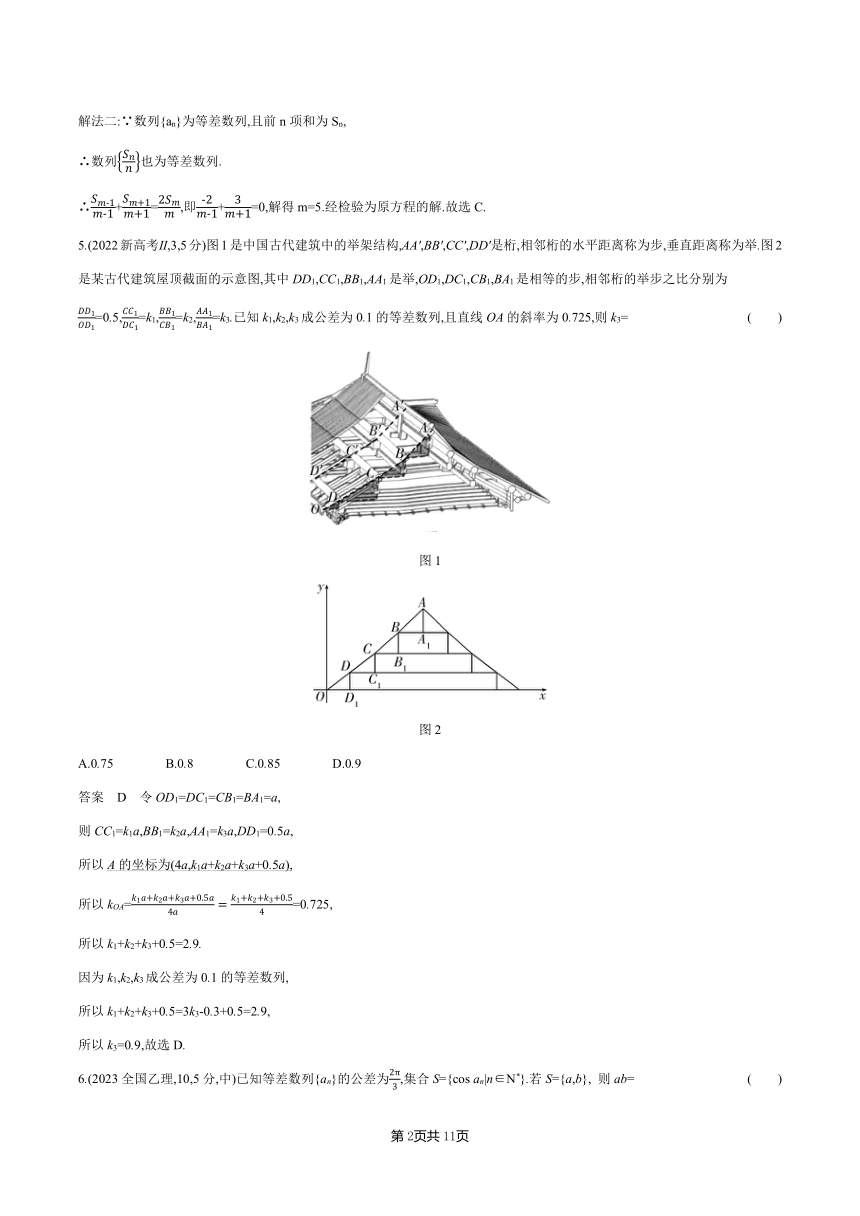
5.(2022新高考Ⅱ,3,5分)图1是中国古代建筑中的举架结构,AA',BB',CC',DD'是桁,相邻桁的水平距离称为步,垂直距离称为举.图2是某古代建筑屋顶截面的示意图,其中DD1,CC1,BB1,AA1是举,OD1,DC1,CB1,BA1是相等的步,相邻桁的举步之比分别为=0.5,=k1,=k2,=k3.已知k1,k2,k3成公差为0.1的等差数列,且直线OA的斜率为0.725,则k3= ( )
图1
图2
A.0.75 B.0.8 C.0.85 D.0.9
答案 D 令OD1=DC1=CB1=BA1=a,
则CC1=k1a,BB1=k2a,AA1=k3a,DD1=0.5a,
所以A的坐标为(4a,k1a+k2a+k3a+0.5a),
所以kOA==0.725,
所以k1+k2+k3+0.5=2.9.
因为k1,k2,k3成公差为0.1的等差数列,
所以k1+k2+k3+0.5=3k3-0.3+0.5=2.9,
所以k3=0.9,故选D.
6.(2023全国乙理,10,5分,中)已知等差数列{an}的公差为,集合S={cos an|n∈N*}.若S={a,b}, 则ab= ( )
A.-1 B.-
答案 B 由题意,得an=a1+(n-1)·,又S={cos an|n∈N*}={a,b},∴cos a1≠cos a2,但cos a1=cos a3,即cos a1=cos,∴a1+a1+=2kπ(k∈Z),∴a1=-+kπ(k∈Z).不妨取k=1,则a1=,a2==π,则S=={a,b},∴ab=-1×.故选B.
7.(2023全国甲文,5,5分,易)记Sn为等差数列{an}的前n项和.若a2+a6=10,a4a8=45,则S5= ( )
A.25 B.22 C.20 D.15
答案 C 设等差数列{an}的公差为d,由已知可得解得∴S5=5a1+×d=5×2+10×1=20.故选C.
8.(2020课标Ⅱ文,14,5分)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2,则S10= .
答案 25
解析 设等差数列{an}的公差为d,
则a2=-2+d,a6=-2+5d,
因为a2+a6=2,所以-2+d+(-2+5d)=2,解得d=1,
所以S10=10×(-2)+×1=-20+45=25.
9.(2019课标Ⅲ文,14,5分)记Sn为等差数列{an}的前n项和.若a3=5,a7=13,则S10= .
答案 100
解析 本题考查等差数列的性质和前n项和公式,考查学生的运算求解能力,考查数学运算的核心素养.
设等差数列{an}的公差为d,则d===2,
∴a1=a3-2d=5-4=1.∴S10=10+×2=100.
失分警示 对等差数列前n项和公式记忆不清,从而导致出错.
10.(2016北京理,12,5分)已知{an}为等差数列,Sn为其前n项和.若a1=6,a3+a5=0,则S6= .
答案 6
解析 设等差数列{an}的公差为d,∵a1=6,a3+a5=0,
∴6+2d+6+4d=0,∴d=-2,∴S6=6×6+×(-2)=6.
评析 本题考查等差数列的前n项和公式,属容易题.
11.(2014天津理,11,5分)设{an}是首项为a1,公差为-1的等差数列,Sn为其前n项和.若S1,S2,S4成等比数列,则a1的值为 .
答案 -
解析 S1=a1,S2=2a1-1,S4=4a1-6.故(2a1-1)2=a1×(4a1-6),解得a1=-.
12.(2022全国乙文,13,5分)记Sn为等差数列{an}的前n项和.若2S3=3S2+6,则公差d= .
答案 2
解析 ∵2S3=3S2+6,∴2(3a1+3d)=3(2a1+d)+6,即6d=3d+6,解得d=2.
13.(2013课标Ⅱ文,17,12分)已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
解析 (1)设{an}的公差为d.由题意,得=a1a13,
即(a1+10d)2=a1(a1+12d).
于是d(2a1+25d)=0.
又a1=25,所以d=0(舍去)或d=-2.
故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.
由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.从而
Sn=(a1+a3n-2)
=(-6n+56)
=-3n2+28n.
14.(2012湖北,理18,文20,12分)已知等差数列{an}前三项的和为-3,前三项的积为8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和.
解析 (1)设等差数列{an}的公差为d,则a2=a1+d,a3=a1+2d,由题意得
解得或
所以由等差数列通项公式可得an=2-3(n-1)=-3n+5或an=-4+3(n-1)=3n-7.
故an=-3n+5或an=3n-7.
(2)当an=-3n+5时,a2,a3,a1分别为-1,-4,2,不成等比数列;
当an=3n-7时,a2,a3,a1分别为-1,2,-4,成等比数列,满足条件.
故|an|=|3n-7|=
记数列{|an|}的前n项和为Sn.
当n=1时,S1=|a1|=4;当n=2时,S2=|a1|+|a2|=5;
当n≥3时,Sn=S2+|a3|+|a4|+…+|an|=5+(3×3-7)+(3×4-7)+…+(3n-7)
=5+=n2-n+10.
当n=2时,满足此式,
综上,Sn=
评析 本题考查等差、等比数列的基础知识,考查运算求解能力.
15.(2016天津,18,13分)已知{an}是各项均为正数的等差数列,公差为d.对任意的n∈N*,bn是an和an+1的等比中项.
(1)设cn=-,n∈N*,求证:数列{cn}是等差数列;
(2)设a1=d,Tn=(-1)k,n∈N*,求证:<.
证明 (1)由题意得=anan+1,有cn=-=an+1an+2-anan+1=2dan+1,因此cn+1-cn=2d(an+2-an+1)=2d2,
所以{cn}是等差数列.
Tn=(-+)+(-+)+…+(-+)=2d(a2+a4+…+a2n)=2d·=2d2n(n+1).所以===·<.
16.(2022全国甲,理17,文18,12分)记Sn为数列{an}的前n项和.已知+n=2an+1.
(1)证明:{an}是等差数列;
(2)若a4,a7,a9成等比数列,求Sn的最小值.
解析 (1)证明:由已知条件+n=2an+1可得,
2Sn=2nan+n-n2①,当n≥2时,由①可得2Sn-1=2(n-1)·an-1+(n-1)-(n-1)2②,由an=Sn-Sn-1及①-②可得,(2n-2)an-(2n-2)an-1=2n-2,n≥2,且n∈N*,
即an-an-1=1,因此{an}是等差数列,公差为1.
(2)∵a4,a7,a9成等比数列,且a4=a1+3,a7=a1+6,a9=a1+8,∴=a4·a9,即(a1+6)2=(a1+3)(a1+8),
解得a1=-12,∴等差数列{an}的通项公式为an=-12+(n-1)·1=n-13,
∴Sn=,
∵n∈N*,∴当n=12或n=13时,Sn最小,
最小值为-78.
17.(2021全国乙理,19,12分)记Sn为数列{an}的前n项和,bn为数列{Sn}的前n项积,已知=2.
(1)证明:数列{bn}是等差数列;
(2)求{an}的通项公式.
解析 (1)证明:由bn=S1·S2·…·Sn可得,
Sn=
由=2知,
当n=1时,=2,即=2,所以b1=S1=,
当n≥2时,=2,即2bn=2bn-1+1,即bn-bn-1=,
故数列{bn}是首项为,公差为的等差数列.
(2)由(1)知,bn=+(n-1)×,
故当n≥2时,Sn=,S1也符合该式,
即Sn=(n∈N*),
从而a1=S1=,
当n≥2时,an=Sn-Sn-1=,a1不符合该式,
所以an=
18.(2022浙江,20,15分)已知等差数列{an}的首项a1=-1,公差d>1.记{an}的前n项和为Sn(n∈N*).
(1)若S4-2a2a3+6=0,求Sn;
(2)若对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,求d的取值范围.
解析 (1)∵{an}为等差数列,∴an=(n-1)d-1,
∴S4-2a2a3+6=6d-4-2(d-1)(2d-1)+6=0,
解得d=3或d=0,又d>1,∴d=3,则an=3n-4,n∈N*,
Sn=,n∈N*.
(2)∵an+cn,an+1+4cn,an+2+15cn成等比数列,
∴(an+1+4cn)2=(an+cn)(an+2+15cn),
∴+(an+2+15an)cn=+(an+2+15an)cn,
∴+(8an+1-an+2-15an)cn+d2=0,
由(1)知an=(n-1)d-1,
∴8an+1-an+2-15an=8+(14-8n)d,
则有+[8+(14-8n)d]cn+d2=0对每个n∈N*都成立,
∴Δ=[8+(14-8n)d]2-4d2=[8+(16-8n)d][8+(12-8n)d]≥0对每个n∈N*都成立,
即≥0对每个n∈N*都成立,
由于n为正整数,d>1,∴+2和只能同处于相邻的整数之间,又∵2<+2<3,∴2≤<3,
∴19.(2021全国甲文,18,12分)记Sn为数列{an}的前n项和,已知an>0,a2=3a1,且数列{}是等差数列.证明:{an}是等差数列.
解题指导:根据已知条件{}为等差数列,求出数列{Sn}的通项公式,利用an=Sn-Sn-1(n≥2,n∈N*)即可求出{an}的通项公式,根据等差数列的定义可证明其为等差数列.
解析 设等差数列{}的公差为d,因为a2=3a1,,所以d=,所以+(n-1),所以Sn=n2a1.
当n≥2时,Sn-1=(n-1)2a1,所以an=Sn-Sn-1=n2a1-(n-1)2a1=(2n-1)a1,经检验,当n=1时,也满足题意,
所以an=(2n-1)a1,n∈N*,
当n≥2时,an-an-1=(2n-1)a1-(2n-3)a1=2a1(常数),
∴{an}是等差数列.
易错警示 应用an=时,不要忽略n=1时的情况.
20.(2021全国甲理,18,12分)已知数列{an}的各项均为正数,记Sn为{an}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立.
①数列{an}是等差数列;②数列{}是等差数列;③a2=3a1.
注:若选择不同的组合分别解答,则按第一个解答计分.
解题指导:先选两个作为条件,余下一个作为结论,然后进行证明.如果是证明③,利用等差中项法,即只需2,通过化简即可得证;如果是证明①或②,可先求数列的通项公式,再利用等差数列的定义证明即可.
解析 选①②作为条件,证明③.
证明:设等差数列{an}的公差为d,因为{}是等差数列,所以2,即2,两边平方,得4(2a1+d)=a1+3a1+3d+2,整理得4a1+d=2,两边平方,得16+8a1d+d2=4(3+3a1d),化简得4-4a1d+d2=0,即=0,所以d=2a1,则a2=a1+d=3a1.
选①③作为条件,证明②.
证明:设等差数列{an}的公差为d.
因为a2=3a1,即a1+d=3a1,所以d=2a1.
所以等差数列{an}的前n项和Sn=na1+·2a1=n2a1.又a1>0,所以.
则=(n+1),所以数列{}是公差为的等差数列.
选②③作为条件,证明①.
证明:设等差数列{}的公差为d,因为,所以d=,则等差数列{}的通项公式为+(n-1),所以Sn=n2a1,当n≥2时,an=Sn-Sn-1=n2a1-(n-1)2a1=(2n-1)a1,且当n=1时,上式也成立,所以数列{an}的通项公式为an=(2n-1)a1,则an+1-an=(2n+1)a1-(2n-1)a1=2a1,所以数列{an}是公差为2a1的等差数列.
方法总结:证明数列{an}是等差数列的方法:
(1)定义法:证明an-an-1=d(n≥2,n∈N*),或an+1-an=d(n∈N*);
(2)等差中项法:证明2an=an-1+an+1(n≥2,n∈N*).
21.(2023新课标Ⅰ,20,12分,中)设等差数列{an}的公差为d,且d>1,令bn=,记Sn,Tn分别为数列{an},{bn}的前n项和.
(1)若3a2=3a1+a3,S3+T3=21,求{an}的通项公式;
(2)若{bn}为等差数列,且S99-T99=99,求d.
解析 (1)∵3a2=3a1+a3,∴3(a1+d)=3a1+a1+2d,
∴a1=d>1,∴S3=a1+a2+a3=a1+a1+d+a1+2d=6a1,
又∵bn=,∴b1=,b2===,b3===,∴T3=b1+b2+b3=,
∴S3+T3=6a1+=21,
解得a1=3或a1=(舍),∴an=3n.
(2)∵{bn}为等差数列,
∴2b2=b1+b3,即=+,
即=+,即-3a1d+2d2=0,
∴a1=2d或a1=d.
当a1=2d时,an=(n+1)d,bn=,
∴S99==99×51d,
T99=·=,
又∵S99-T99=99,∴99×51d-99×50·=99,
∴51d-=1,解得d=1或d=-,
又∵d>1,∴a1≠2d.
当a1=d时,an=nd,bn=,
∴S99==50×99d,
T99=·=,
又∵S99-T99=99,∴50×99d-=99,
∴50d-=1,解得d=或d=-1,
又∵d>1,∴d=.
综上,d=.
22.(2023全国乙文,18,12分,中)记Sn为等差数列{an}的前n项和,已知a2=11,S10=40.
(1)求{an}的通项公式;
(2)求数列{|an|}的前n项和Tn.
解析 (1)设等差数列{an}的公差为d,
则解得
∴an=13-2(n-1)=15-2n.
(2)由an=15-2n知,当n≤7,n∈N*时,an>0,当n≥8,n∈N*时,an<0,
∴当n≤7,n∈N*时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn==-n2+14n,
当n≥8,n∈N*时,Tn=(a1+a2+…+a7)-(a8+a9+…+an)
=2S7-Sn=98-(-n2+14n)=n2-14n+98.
∴Tn=
考点二 等差数列的性质
1.(2021北京,6,4分)已知{an}和{bn}是两个等差数列,且(1≤k≤5)是常数,若a1=288,a5=96,b1=192,则b3的值为 ( )
A.64 B.100 C.128 D.132
答案 C 命题意图:本题以定义新运算为出题背景,考查等差数列的性质,考查学生的运算求解能力,考查的核心素养是逻辑推理及数学运算,落实了应用性、综合性和创新性的考查要求.
解题思路:解法一:因为{an}是等差数列,所以2a3=a1+a5=288+96,所以a3=192,又因为当1≤k≤5时,是常值,所以,即,从而b3=128.
解法二:由题意可知,则b5=64,又{bn}是等差数列,所以b3==128.
2.(2020课标Ⅱ理,4,5分)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石) ( )
A.3 699块 B.3 474块 C.3 402块 D.3 339块
答案 C 由题意可设每层有n个环,则三层共有3n个环,∴每一环扇面形石板的块数构成以a1=9为首项,9为公差的等差数列{an},且项数为3n.不妨设上层扇面形石板总数为S1,中层总数为S2,下层总数为S3,∴S3-S2==9n2=729,解得n=9(负值舍去).
则三层共有扇面形石板(不含天心石)27×9+×9=27×9+27×13×9=27×14×9=3 402(块).故选C.
3.(2015课标Ⅱ文,5,5分)设Sn是等差数列{an}的前n项和.若a1+a3+a5=3,则S5=( )
A.5 B.7 C.9 D.11
答案 A ∵{an}为等差数列,∴a1+a5=2a3,
得3a3=3,则a3=1,
∴S5==5a3=5,故选A.
4.(2015广东理,10,5分)在等差数列{an}中,若a3+a4+a5+a6+a7=25,则a2+a8= .
答案 10
解析 利用等差数列的性质可得a3+a7=a4+a6=2a5,从而a3+a4+a5+a6+a7=5a5=25,故a5=5,所以a2+a8=2a5=10.
5.(2015陕西文,13,5分)中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为 .
答案 5
解析 设该数列的首项为a1,根据等差数列的性质可得a1+2015=2×1010,从而a1=5.
6.(2014北京理,12,5分)若等差数列{an}满足a7+a8+a9>0,a7+a10<0,则当n= 时,{an}的前n项和最大.
答案 8
解析 根据题意知a7+a8+a9=3a8>0,即a8>0.
又a8+a9=a7+a10<0,∴a9<0,∴当n=8时,{an}的前n项和最大.
(
第
1
页共
5
页
)
6.2 等差数列
考点一 等差数列及其前n项和
1.(2016课标Ⅰ,3,5分)已知等差数列{an}前9项的和为27,a10=8,则a100=( )
A.100 B.99 C.98 D.97
答案 C 设{an}的公差为d,由等差数列前n项和公式及通项公式,得解得∴an=a1+(n-1)·d=n-2,∴a100=100-2=98.故选C.
方法总结 已知条件中有具体的an、Sn的值时,通常用基本量法处理,即在a1、d、n、an、Sn这5个量中知三求二.
一题多解 由S9=·9=·9=9a5=27,可得a5=3,
所以a10-a5=5d=5,所以d=1,
所以a100=a10+90d=98.故选C.
2.(2015课标Ⅰ文,7,5分)已知{an}是公差为1的等差数列,Sn为{an}的前n项和.若S8=4S4,则a10=( )
A. B. C.10 D.12
答案 B 由S8=4S4得8a1+×1=4×,解得a1=,∴a10=a1+9d=,故选B.
评析 本题主要考查等差数列的前n项和,计算准确是解题关键,属容易题.
3.(2015浙江理,3,5分)已知{an}是等差数列,公差d不为零,前n项和是Sn.若a3,a4,a8成等比数列,则( )
A.a1d>0,dS4>0 B.a1d<0,dS4<0
C.a1d>0,dS4<0 D.a1d<0,dS4>0
答案 B 由=a3a8,得(a1+2d)(a1+7d)=(a1+3d)2,整理得d(5d+3a1)=0,又d≠0,∴a1=-d,则a1d=-d2<0,又∵S4=4a1+6d=-d,∴dS4=-d2<0,故选B.
4.(2013课标Ⅰ理,7,5分)设等差数列{an}的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m=( )
A.3 B.4 C.5 D.6
答案 C 解法一:∵Sm-1=-2,Sm=0,Sm+1=3,∴am=Sm-Sm-1=2,am+1=Sm+1-Sm=3,∴公差d=am+1-am=1,由Sn=na1+d=na1+,
得
由①得a1=,代入②可得m=5.
解法二:∵数列{an}为等差数列,且前n项和为Sn,
∴数列也为等差数列.
∴+=,即+=0,解得m=5.经检验为原方程的解.故选C.
5.(2022新高考Ⅱ,3,5分)图1是中国古代建筑中的举架结构,AA',BB',CC',DD'是桁,相邻桁的水平距离称为步,垂直距离称为举.图2是某古代建筑屋顶截面的示意图,其中DD1,CC1,BB1,AA1是举,OD1,DC1,CB1,BA1是相等的步,相邻桁的举步之比分别为=0.5,=k1,=k2,=k3.已知k1,k2,k3成公差为0.1的等差数列,且直线OA的斜率为0.725,则k3= ( )
图1
图2
A.0.75 B.0.8 C.0.85 D.0.9
答案 D 令OD1=DC1=CB1=BA1=a,
则CC1=k1a,BB1=k2a,AA1=k3a,DD1=0.5a,
所以A的坐标为(4a,k1a+k2a+k3a+0.5a),
所以kOA==0.725,
所以k1+k2+k3+0.5=2.9.
因为k1,k2,k3成公差为0.1的等差数列,
所以k1+k2+k3+0.5=3k3-0.3+0.5=2.9,
所以k3=0.9,故选D.
6.(2023全国乙理,10,5分,中)已知等差数列{an}的公差为,集合S={cos an|n∈N*}.若S={a,b}, 则ab= ( )
A.-1 B.-
答案 B 由题意,得an=a1+(n-1)·,又S={cos an|n∈N*}={a,b},∴cos a1≠cos a2,但cos a1=cos a3,即cos a1=cos,∴a1+a1+=2kπ(k∈Z),∴a1=-+kπ(k∈Z).不妨取k=1,则a1=,a2==π,则S=={a,b},∴ab=-1×.故选B.
7.(2023全国甲文,5,5分,易)记Sn为等差数列{an}的前n项和.若a2+a6=10,a4a8=45,则S5= ( )
A.25 B.22 C.20 D.15
答案 C 设等差数列{an}的公差为d,由已知可得解得∴S5=5a1+×d=5×2+10×1=20.故选C.
8.(2020课标Ⅱ文,14,5分)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2,则S10= .
答案 25
解析 设等差数列{an}的公差为d,
则a2=-2+d,a6=-2+5d,
因为a2+a6=2,所以-2+d+(-2+5d)=2,解得d=1,
所以S10=10×(-2)+×1=-20+45=25.
9.(2019课标Ⅲ文,14,5分)记Sn为等差数列{an}的前n项和.若a3=5,a7=13,则S10= .
答案 100
解析 本题考查等差数列的性质和前n项和公式,考查学生的运算求解能力,考查数学运算的核心素养.
设等差数列{an}的公差为d,则d===2,
∴a1=a3-2d=5-4=1.∴S10=10+×2=100.
失分警示 对等差数列前n项和公式记忆不清,从而导致出错.
10.(2016北京理,12,5分)已知{an}为等差数列,Sn为其前n项和.若a1=6,a3+a5=0,则S6= .
答案 6
解析 设等差数列{an}的公差为d,∵a1=6,a3+a5=0,
∴6+2d+6+4d=0,∴d=-2,∴S6=6×6+×(-2)=6.
评析 本题考查等差数列的前n项和公式,属容易题.
11.(2014天津理,11,5分)设{an}是首项为a1,公差为-1的等差数列,Sn为其前n项和.若S1,S2,S4成等比数列,则a1的值为 .
答案 -
解析 S1=a1,S2=2a1-1,S4=4a1-6.故(2a1-1)2=a1×(4a1-6),解得a1=-.
12.(2022全国乙文,13,5分)记Sn为等差数列{an}的前n项和.若2S3=3S2+6,则公差d= .
答案 2
解析 ∵2S3=3S2+6,∴2(3a1+3d)=3(2a1+d)+6,即6d=3d+6,解得d=2.
13.(2013课标Ⅱ文,17,12分)已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
解析 (1)设{an}的公差为d.由题意,得=a1a13,
即(a1+10d)2=a1(a1+12d).
于是d(2a1+25d)=0.
又a1=25,所以d=0(舍去)或d=-2.
故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.
由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.从而
Sn=(a1+a3n-2)
=(-6n+56)
=-3n2+28n.
14.(2012湖北,理18,文20,12分)已知等差数列{an}前三项的和为-3,前三项的积为8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和.
解析 (1)设等差数列{an}的公差为d,则a2=a1+d,a3=a1+2d,由题意得
解得或
所以由等差数列通项公式可得an=2-3(n-1)=-3n+5或an=-4+3(n-1)=3n-7.
故an=-3n+5或an=3n-7.
(2)当an=-3n+5时,a2,a3,a1分别为-1,-4,2,不成等比数列;
当an=3n-7时,a2,a3,a1分别为-1,2,-4,成等比数列,满足条件.
故|an|=|3n-7|=
记数列{|an|}的前n项和为Sn.
当n=1时,S1=|a1|=4;当n=2时,S2=|a1|+|a2|=5;
当n≥3时,Sn=S2+|a3|+|a4|+…+|an|=5+(3×3-7)+(3×4-7)+…+(3n-7)
=5+=n2-n+10.
当n=2时,满足此式,
综上,Sn=
评析 本题考查等差、等比数列的基础知识,考查运算求解能力.
15.(2016天津,18,13分)已知{an}是各项均为正数的等差数列,公差为d.对任意的n∈N*,bn是an和an+1的等比中项.
(1)设cn=-,n∈N*,求证:数列{cn}是等差数列;
(2)设a1=d,Tn=(-1)k,n∈N*,求证:<.
证明 (1)由题意得=anan+1,有cn=-=an+1an+2-anan+1=2dan+1,因此cn+1-cn=2d(an+2-an+1)=2d2,
所以{cn}是等差数列.
Tn=(-+)+(-+)+…+(-+)=2d(a2+a4+…+a2n)=2d·=2d2n(n+1).所以===·<.
16.(2022全国甲,理17,文18,12分)记Sn为数列{an}的前n项和.已知+n=2an+1.
(1)证明:{an}是等差数列;
(2)若a4,a7,a9成等比数列,求Sn的最小值.
解析 (1)证明:由已知条件+n=2an+1可得,
2Sn=2nan+n-n2①,当n≥2时,由①可得2Sn-1=2(n-1)·an-1+(n-1)-(n-1)2②,由an=Sn-Sn-1及①-②可得,(2n-2)an-(2n-2)an-1=2n-2,n≥2,且n∈N*,
即an-an-1=1,因此{an}是等差数列,公差为1.
(2)∵a4,a7,a9成等比数列,且a4=a1+3,a7=a1+6,a9=a1+8,∴=a4·a9,即(a1+6)2=(a1+3)(a1+8),
解得a1=-12,∴等差数列{an}的通项公式为an=-12+(n-1)·1=n-13,
∴Sn=,
∵n∈N*,∴当n=12或n=13时,Sn最小,
最小值为-78.
17.(2021全国乙理,19,12分)记Sn为数列{an}的前n项和,bn为数列{Sn}的前n项积,已知=2.
(1)证明:数列{bn}是等差数列;
(2)求{an}的通项公式.
解析 (1)证明:由bn=S1·S2·…·Sn可得,
Sn=
由=2知,
当n=1时,=2,即=2,所以b1=S1=,
当n≥2时,=2,即2bn=2bn-1+1,即bn-bn-1=,
故数列{bn}是首项为,公差为的等差数列.
(2)由(1)知,bn=+(n-1)×,
故当n≥2时,Sn=,S1也符合该式,
即Sn=(n∈N*),
从而a1=S1=,
当n≥2时,an=Sn-Sn-1=,a1不符合该式,
所以an=
18.(2022浙江,20,15分)已知等差数列{an}的首项a1=-1,公差d>1.记{an}的前n项和为Sn(n∈N*).
(1)若S4-2a2a3+6=0,求Sn;
(2)若对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,求d的取值范围.
解析 (1)∵{an}为等差数列,∴an=(n-1)d-1,
∴S4-2a2a3+6=6d-4-2(d-1)(2d-1)+6=0,
解得d=3或d=0,又d>1,∴d=3,则an=3n-4,n∈N*,
Sn=,n∈N*.
(2)∵an+cn,an+1+4cn,an+2+15cn成等比数列,
∴(an+1+4cn)2=(an+cn)(an+2+15cn),
∴+(an+2+15an)cn=+(an+2+15an)cn,
∴+(8an+1-an+2-15an)cn+d2=0,
由(1)知an=(n-1)d-1,
∴8an+1-an+2-15an=8+(14-8n)d,
则有+[8+(14-8n)d]cn+d2=0对每个n∈N*都成立,
∴Δ=[8+(14-8n)d]2-4d2=[8+(16-8n)d][8+(12-8n)d]≥0对每个n∈N*都成立,
即≥0对每个n∈N*都成立,
由于n为正整数,d>1,∴+2和只能同处于相邻的整数之间,又∵2<+2<3,∴2≤<3,
∴
解题指导:根据已知条件{}为等差数列,求出数列{Sn}的通项公式,利用an=Sn-Sn-1(n≥2,n∈N*)即可求出{an}的通项公式,根据等差数列的定义可证明其为等差数列.
解析 设等差数列{}的公差为d,因为a2=3a1,,所以d=,所以+(n-1),所以Sn=n2a1.
当n≥2时,Sn-1=(n-1)2a1,所以an=Sn-Sn-1=n2a1-(n-1)2a1=(2n-1)a1,经检验,当n=1时,也满足题意,
所以an=(2n-1)a1,n∈N*,
当n≥2时,an-an-1=(2n-1)a1-(2n-3)a1=2a1(常数),
∴{an}是等差数列.
易错警示 应用an=时,不要忽略n=1时的情况.
20.(2021全国甲理,18,12分)已知数列{an}的各项均为正数,记Sn为{an}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立.
①数列{an}是等差数列;②数列{}是等差数列;③a2=3a1.
注:若选择不同的组合分别解答,则按第一个解答计分.
解题指导:先选两个作为条件,余下一个作为结论,然后进行证明.如果是证明③,利用等差中项法,即只需2,通过化简即可得证;如果是证明①或②,可先求数列的通项公式,再利用等差数列的定义证明即可.
解析 选①②作为条件,证明③.
证明:设等差数列{an}的公差为d,因为{}是等差数列,所以2,即2,两边平方,得4(2a1+d)=a1+3a1+3d+2,整理得4a1+d=2,两边平方,得16+8a1d+d2=4(3+3a1d),化简得4-4a1d+d2=0,即=0,所以d=2a1,则a2=a1+d=3a1.
选①③作为条件,证明②.
证明:设等差数列{an}的公差为d.
因为a2=3a1,即a1+d=3a1,所以d=2a1.
所以等差数列{an}的前n项和Sn=na1+·2a1=n2a1.又a1>0,所以.
则=(n+1),所以数列{}是公差为的等差数列.
选②③作为条件,证明①.
证明:设等差数列{}的公差为d,因为,所以d=,则等差数列{}的通项公式为+(n-1),所以Sn=n2a1,当n≥2时,an=Sn-Sn-1=n2a1-(n-1)2a1=(2n-1)a1,且当n=1时,上式也成立,所以数列{an}的通项公式为an=(2n-1)a1,则an+1-an=(2n+1)a1-(2n-1)a1=2a1,所以数列{an}是公差为2a1的等差数列.
方法总结:证明数列{an}是等差数列的方法:
(1)定义法:证明an-an-1=d(n≥2,n∈N*),或an+1-an=d(n∈N*);
(2)等差中项法:证明2an=an-1+an+1(n≥2,n∈N*).
21.(2023新课标Ⅰ,20,12分,中)设等差数列{an}的公差为d,且d>1,令bn=,记Sn,Tn分别为数列{an},{bn}的前n项和.
(1)若3a2=3a1+a3,S3+T3=21,求{an}的通项公式;
(2)若{bn}为等差数列,且S99-T99=99,求d.
解析 (1)∵3a2=3a1+a3,∴3(a1+d)=3a1+a1+2d,
∴a1=d>1,∴S3=a1+a2+a3=a1+a1+d+a1+2d=6a1,
又∵bn=,∴b1=,b2===,b3===,∴T3=b1+b2+b3=,
∴S3+T3=6a1+=21,
解得a1=3或a1=(舍),∴an=3n.
(2)∵{bn}为等差数列,
∴2b2=b1+b3,即=+,
即=+,即-3a1d+2d2=0,
∴a1=2d或a1=d.
当a1=2d时,an=(n+1)d,bn=,
∴S99==99×51d,
T99=·=,
又∵S99-T99=99,∴99×51d-99×50·=99,
∴51d-=1,解得d=1或d=-,
又∵d>1,∴a1≠2d.
当a1=d时,an=nd,bn=,
∴S99==50×99d,
T99=·=,
又∵S99-T99=99,∴50×99d-=99,
∴50d-=1,解得d=或d=-1,
又∵d>1,∴d=.
综上,d=.
22.(2023全国乙文,18,12分,中)记Sn为等差数列{an}的前n项和,已知a2=11,S10=40.
(1)求{an}的通项公式;
(2)求数列{|an|}的前n项和Tn.
解析 (1)设等差数列{an}的公差为d,
则解得
∴an=13-2(n-1)=15-2n.
(2)由an=15-2n知,当n≤7,n∈N*时,an>0,当n≥8,n∈N*时,an<0,
∴当n≤7,n∈N*时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn==-n2+14n,
当n≥8,n∈N*时,Tn=(a1+a2+…+a7)-(a8+a9+…+an)
=2S7-Sn=98-(-n2+14n)=n2-14n+98.
∴Tn=
考点二 等差数列的性质
1.(2021北京,6,4分)已知{an}和{bn}是两个等差数列,且(1≤k≤5)是常数,若a1=288,a5=96,b1=192,则b3的值为 ( )
A.64 B.100 C.128 D.132
答案 C 命题意图:本题以定义新运算为出题背景,考查等差数列的性质,考查学生的运算求解能力,考查的核心素养是逻辑推理及数学运算,落实了应用性、综合性和创新性的考查要求.
解题思路:解法一:因为{an}是等差数列,所以2a3=a1+a5=288+96,所以a3=192,又因为当1≤k≤5时,是常值,所以,即,从而b3=128.
解法二:由题意可知,则b5=64,又{bn}是等差数列,所以b3==128.
2.(2020课标Ⅱ理,4,5分)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石) ( )
A.3 699块 B.3 474块 C.3 402块 D.3 339块
答案 C 由题意可设每层有n个环,则三层共有3n个环,∴每一环扇面形石板的块数构成以a1=9为首项,9为公差的等差数列{an},且项数为3n.不妨设上层扇面形石板总数为S1,中层总数为S2,下层总数为S3,∴S3-S2==9n2=729,解得n=9(负值舍去).
则三层共有扇面形石板(不含天心石)27×9+×9=27×9+27×13×9=27×14×9=3 402(块).故选C.
3.(2015课标Ⅱ文,5,5分)设Sn是等差数列{an}的前n项和.若a1+a3+a5=3,则S5=( )
A.5 B.7 C.9 D.11
答案 A ∵{an}为等差数列,∴a1+a5=2a3,
得3a3=3,则a3=1,
∴S5==5a3=5,故选A.
4.(2015广东理,10,5分)在等差数列{an}中,若a3+a4+a5+a6+a7=25,则a2+a8= .
答案 10
解析 利用等差数列的性质可得a3+a7=a4+a6=2a5,从而a3+a4+a5+a6+a7=5a5=25,故a5=5,所以a2+a8=2a5=10.
5.(2015陕西文,13,5分)中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为 .
答案 5
解析 设该数列的首项为a1,根据等差数列的性质可得a1+2015=2×1010,从而a1=5.
6.(2014北京理,12,5分)若等差数列{an}满足a7+a8+a9>0,a7+a10<0,则当n= 时,{an}的前n项和最大.
答案 8
解析 根据题意知a7+a8+a9=3a8>0,即a8>0.
又a8+a9=a7+a10<0,∴a9<0,∴当n=8时,{an}的前n项和最大.
(
第
1
页共
5
页
)
同课章节目录
