2014-2023年高考数学真题专题分类--7.2 简单的线性规划(含解析)
文档属性
| 名称 | 2014-2023年高考数学真题专题分类--7.2 简单的线性规划(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 693.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 17:15:26 | ||
图片预览




文档简介
2014-2023年高考数学真题专题分类
7.2 简单的线性规划
考点 简单的线性规划
1.(2018天津理,2文,2,5分)设变量x,y满足约束条件则目标函数z=3x+5y的最大值为( )
A.6 B.19 C.21 D.45
答案 C 本题主要考查线性目标函数最值的求解.
由变量x,y满足的约束条件画出可行域(如图阴影部分所示).
作出基本直线l0:3x+5y=0,平移直线l0,当经过点A(2,3)时,z取最大值,zmax=3×2+5×3=21,故选C.
2.(2018北京理,8,5分)设集合A={(x,y)|x-y≥1,ax+y>4,x-ay≤2},则( )
A.对任意实数a,(2,1)∈A
B.对任意实数a,(2,1) A
C.当且仅当a<0时,(2,1) A
D.当且仅当a≤时,(2,1) A
答案 D 本题主要考查不等式组的解法,元素与集合的关系.
若(2,1)∈A,则有解得a>.结合四个选项,只有D说法正确.故选D.
易错警示 注意区分集合条件中的“或”与“且”.本题容易把三个不等式的中间联结词认为是“或”而错选A.
3.(2017课标Ⅲ文,5,5分)设x,y满足约束条件则z=x-y的取值范围是( )
A.[-3,0] B.[-3,2] C.[0,2] D.[0,3]
答案 B 由题意,画出可行域(如图中阴影部分所示),易知A(0,3),B(2,0).
由图可知,目标函数z=x-y在点A,B处分别取得最小值与最大值,zmin=0-3=-3,zmax=2-0=2,
故z=x-y的取值范围是[-3,2].故选B.
4.(2017课标Ⅰ文,7,5分)设x,y满足约束条件则z=x+y的最大值为( )
A.0 B.1 C.2 D.3
答案 D 本题考查简单的线性规划问题.
作出约束条件表示的可行域如图:
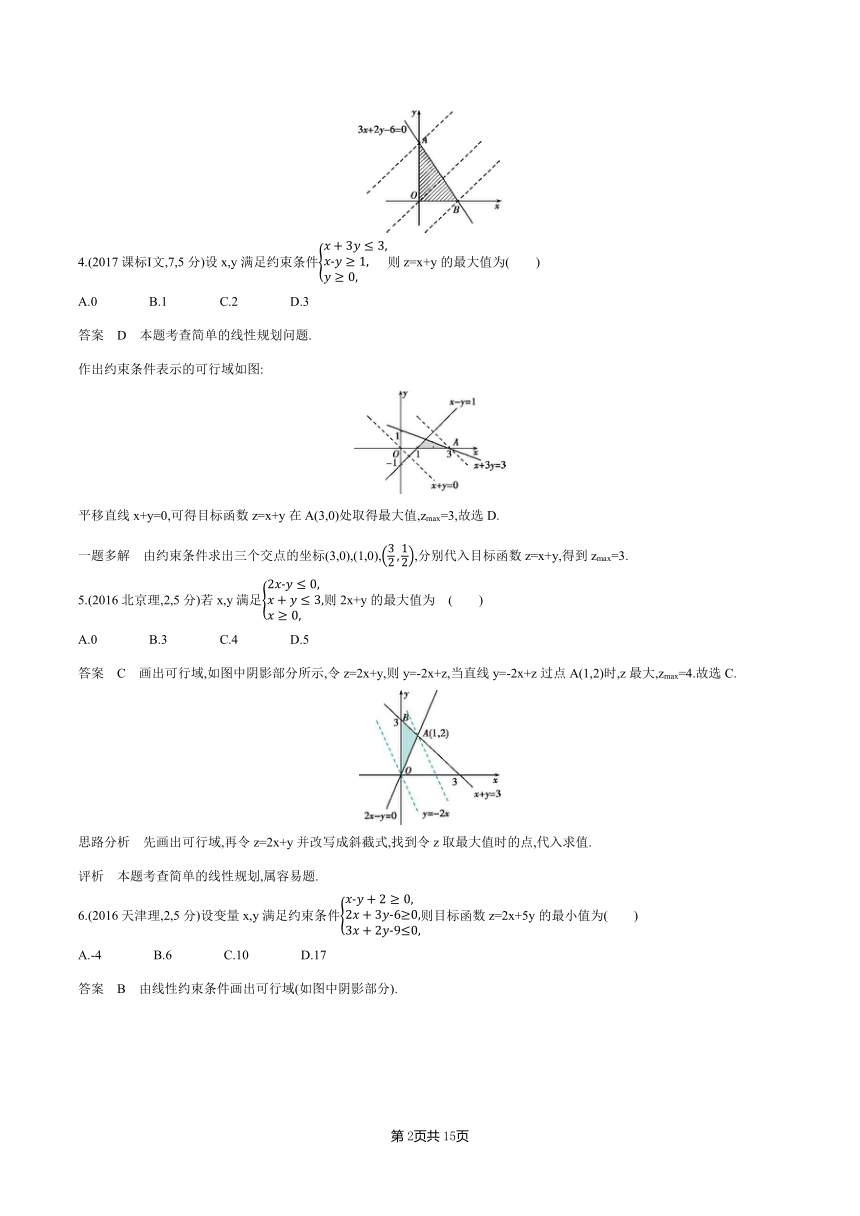
平移直线x+y=0,可得目标函数z=x+y在A(3,0)处取得最大值,zmax=3,故选D.
一题多解 由约束条件求出三个交点的坐标(3,0),(1,0),,分别代入目标函数z=x+y,得到zmax=3.
5.(2016北京理,2,5分)若x,y满足则2x+y的最大值为 ( )
A.0 B.3 C.4 D.5
答案 C 画出可行域,如图中阴影部分所示,令z=2x+y,则y=-2x+z,当直线y=-2x+z过点A(1,2)时,z最大,zmax=4.故选C.
思路分析 先画出可行域,再令z=2x+y并改写成斜截式,找到令z取最大值时的点,代入求值.
评析 本题考查简单的线性规划,属容易题.
6.(2016天津理,2,5分)设变量x,y满足约束条件则目标函数z=2x+5y的最小值为( )
A.-4 B.6 C.10 D.17
答案 B 由线性约束条件画出可行域(如图中阴影部分).
当直线2x+5y-z=0过点A(3,0)时,zmin=2×3+5×0=6,故选B.
评析 本题考查了简单的线性规划问题,正确画出可行域是求解的关键.
7.(2016山东,4,5分)若变量x,y满足则x2+y2的最大值是( )
A.4 B.9 C.10 D.12
答案 C 作出不等式组所表示的平面区域,如图(阴影部分)所示,
x2+y2表示平面区域内的点到原点的距离的平方,由图易知平面区域内的点A(3,-1)到原点的距离最大,所以x2+y2的最大值是10,故选C.
评析 本题考查了数形结合的思想方法.利用x2+y2的几何意义是求解的关键.
8.(2016浙江,4,5分)若平面区域夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是( )
A. B. C. D.
答案 B 作出可行域如图.
由得A(2,1),
由得B(1,2).
斜率为1的平行直线l1,l2分别过A,B两点时它们之间的距离最小.过A(2,1)的直线l1:y=x-1,过B(1,2)的直线l2:y=x+1,此时两平行直线间的距离d==.故选B.
9.(2015重庆,10,5分)若不等式组表示的平面区域为三角形,且其面积等于,则m的值为( )
A.-3 B.1 C. D.3
答案 B 如图,要使不等式组表示的平面区域为三角形,则-2m<2,即m>-1,所围成的区域为△ABC,S△ABC=S△ADC-S△BDC.
点A的纵坐标为1+m,点B的纵坐标为(1+m),C,D两点的横坐标分别为2,-2m,
所以S△ABC=(2+2m)(1+m)-(2+2m)·(1+m)
=(1+m)2=,
解得m=-3(舍去)或m=1.
故选B.
10.(2015山东理,6,5分)已知x,y满足约束条件若z=ax+y的最大值为4,则a=( )
A.3 B.2 C.-2 D.-3
答案 B 作出可行域如图.
①当a<0时,显然z=ax+y的最大值不为4;②当a=0时,z=y在B(1,1)处取得最大值,为1,不符合题意;③当01时,z=ax+y在A(2,0)处取得最大值,zmax=2a=4,得a=2,符合题意.综上,a=2.
11.(2015福建文,10,5分)变量x,y满足约束条件若z=2x-y的最大值为2,则实数m等于( )
A.-2 B.-1 C.1 D.2
答案 C 当m<0时,约束条件所表示的平面区域是开放的,目标函数z=2x-y无最大值,排除A,B,当m=2时,目标函数z=2x-y的最大值为0,于是排除D,故选C.
12.(2014课标Ⅱ理,9,5分,0.798)设x,y满足约束条件则z=2x-y的最大值为( )
A.10 B.8 C.3 D.2
答案 B 由约束条件得可行域如图阴影部分所示.
由得A(5,2).当直线2x-y=z过点A时,z=2x-y取得最大值.其最大值为2×5-2=8.故选B.
方法总结 解决线性规划问题的一般步骤:①画出可行域;②根据目标函数的几何意义确定其取得最优解的点,并求出该点坐标;③求出目标函数的最大值或最小值.
13.(2014课标Ⅱ文,9,5分,0.700)设x,y满足约束条件则z=x+2y的最大值为( )
A.8 B.7
C.2 D.1
答案 B 约束条件表示的平面区域如图中阴影部分所示,
由z=x+2y,得y=-x+,为直线y=-x+在y轴上的截距,要使z最大,则需最大,所以当直线y=-x+经过点B(3,2)时,z最大,最大值为3+2×2=7,故选B.
14.(2014课标Ⅰ文,11,5分,0.236)设x,y满足约束条件且z=x+ay的最小值为7,则a=( )
A.-5 B.3
C.-5或3 D.5或-3
答案 B 二元一次不等式组表示的平面区域如图所示,其中A.平移直线x+ay=0,可知在点A处,z取得最值,
因此+a×=7,化简得a2+2a-15=0,
解得a=3或a=-5,但a=-5时,z取得最大值,故舍去,故选B.
解后反思 本题也可由排除法选出答案,当a=-5时,目标函数无最小值,当a=3时,可以判断出目标函数的最小值为7,所以选B.
15.(2014北京理,6,5分)若x,y满足且z=y-x的最小值为-4,则k的值为( )
A.2 B.-2 C. D.-
答案 D 由得A(4,0).
由图推测直线kx-y+2=0必过A(4,0),得k=-,经验证符合题目条件.故选D.
16.(2014课标Ⅰ理,9,5分)不等式组的解集记为D.有下面四个命题:
p1: (x,y)∈D,x+2y≥-2,
p2: (x,y)∈D,x+2y≥2,
p3: (x,y)∈D,x+2y≤3,
p4: (x,y)∈D,x+2y≤-1.
其中的真命题是( )
A.p2,p3 B.p1,p2 C.p1,p4 D.p1,p3
答案 B 不等式组表示的平面区域D如图阴影区域所示.设z=x+2y,作出基本直线l0:x+2y=0,经平移可知直线l:z=x+2y经过点A(2,-1)时z取得最小值0,无最大值.对于命题p1:由于z的最小值为0,所以 (x,y)∈D,x+2y≥0恒成立,故x+2y≥-2恒成立,因此命题p1为真命题;由于 (x,y)∈D,x+2y≥0,故 (x,y)∈D,x+2y≥2,因此命题p2为真命题;由于z=x+2y的最小值为0,无最大值,故命题p3与p4错误,故选B.
17.(2013课标Ⅱ文,3,5分,0.693)设x,y满足约束条件则z=2x-3y的最小值是( )
A.-7 B.-6 C.-5 D.-3
答案 B 由约束条件得可行域(如图),当直线2x-3y-z=0过点A(3,4)时,zmin=2×3-3×4=-6.故选B.
18.(2013课标Ⅱ理,9,5分,0.788)已知a>0,x,y满足约束条件若z=2x+y的最小值为1,则a=( )
A. B. C.1 D.2
答案 B 由约束条件画出可行域(如图所示的△ABC及其内部),
由得A(1,-2a),
当直线2x+y-z=0过点A时,z=2x+y取得最小值,所以1=2×1-2a,解得a=,故选B.
解题关键 根据约束条件准确画出可行域,从而经过平移确定直线z=2x+y过可行域内的点A时z取得最小值是解题的关键.
19.(2013湖北文,9,5分)某旅行社租用A、B两种型号的客车安排900名客人旅行,A、B两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆.则租金最少为 ( )
A.31200元 B.36000元 C.36800元 D.38400元
答案 C 设旅行社租用A型客车x辆,B型客车y辆,租金为z元,则线性约束条件为目标函数为z=1600x+2400y.
画出可行域:
当目标函数z=1600x+2400y经过点A(5,12)时,zmin=1600×5+2400×12=36800.选C.
20.(2012课标,5,5分)已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是( )
A.(1-,2) B.(0,2)
C.(-1,2) D.(0,1+)
答案 A 由题意知可行域为△ABC(不含边界).
当直线-x+y-z=0过点C(1+,2)时,zmin=1-;当过点B(1,3)时,zmax=2.故选A.
评析 本题考查了简单的线性规划,考查了数形结合的思想.正确理解直线的斜率、截距的几何意义是求解的关键.
21.(2016浙江,3,5分)在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域中的点在直线x+y-2=0上的投影构成的线段记为AB,则|AB|=( )
A.2 B.4 C.3 D.6
答案 C 由不等式组画出可行域,如图中的阴影部分所示.因为直线x+y-2=0与直线x+y=0平行,所以可行域内的点在直线x+y-2=0上的投影构成的线段的长|AB|即为|CD|.易得C(2,-2),D(-1,1),所以|AB|=|CD|==3.故选C.
22.(2022全国乙文,5,5分)若x,y满足约束条件则z=2x-y的最大值是 ( )
A.-2 B.4 C.8 D.12
答案 C 由约束条件作出可行域如图中阴影部分所示,
联立可得A(4,0),
当直线z=2x-y过点A时,z=2x-y取最大值,
zmax=2×4-0=8,故选C.
23.(2021全国乙文,5,5分)若x,y满足约束条件则z=3x+y的最小值为 ( )
A.18 B.10 C.6 D.4
答案 C 解题指导:思路一:先画出可行域,然后移动直线3x+y=0,最后由z与纵截距的关系得最优解,计算即可;
思路二:先求出可行域顶点的坐标,然后分别求出各顶点处目标函数值,通过比较大小得到z的最小值.
解析 解法一:作出不等式组表示的可行域,如图.
作直线l:3x+y=0,平行移动直线l,可知当平移后的直线过点(1,3)时,纵截距最小,即z最小.故zmin=3×1+3=6.故选C.
解法二:根据线性约束条件得出可行域为△ABC及其内部(如上图所示),其中A(3,1),B(1,3),C(5,3),经检验,知目标直线过点B(1,3)时,z取最小值,即zmin=3×1+3=6.
解后反思:对于直线z=Ax+By,若B>0,则当目标直线向上移动时,z变大;若B<0,则当目标直线向下移动时,z变大.
24.(2020课标Ⅰ理,13,5分)若x,y满足约束条件则z=x+7y的最大值为 .
答案 1
审题指导:作出可行域移动直线x+7y=0过A(1,0)时有zmax.
解题思路:作出可行域如图,由z=x+7y得y=-,易知当直线y=-经过点A(1,0)时,z取得最大值,zmax=1+7×0=1.
方法总结:线性规划问题的最优解一般在可行域的边界或顶点处取得,所以可以通过平移目标函数所对应的直线判断最优解,还可以通过比较边界或顶点处的目标函数值进行判断.
25.(2016江苏,12,5分)已知实数x,y满足则x2+y2的取值范围是 .
答案
解析 画出不等式组表示的可行域如图:
由x-2y+4=0及3x-y-3=0得A(2,3),由x2+y2表示可行域内的点(x,y)与点(0,0)的距离的平方可得(x2+y2)max=22+32=13,(x2+y2)min=d2==,其中d表示点(0,0)到直线2x+y-2=0的距离,所以x2+y2的取值范围为.
解后反思 对于线性规划问题,要正确作出可行域,并理解目标函数的几何意义,分清常规的“距离型”“斜率型”与“截距型”是解题的关键.
26.(2020课标Ⅱ文,15,5分)若x,y满足约束条件则z=x+2y的最大值是 .
答案 8
解析 作出约束条件表示的可行域,如图所示.由图可知直线z=x+2y过点A(2,3)时,z取得最大值,最大值为2+2×3=8.
27.(2019课标Ⅱ文,13,5分)若变量x,y满足约束条件则z=3x-y的最大值是 .
答案 9
解析 本题考查简单的线性规划问题;以二元一次不等式组作为约束条件考查学生数形结合思想及运算求解能力;考查数学运算的核心素养.
作出可行域(如图阴影部分所示).
易得A(3,0),B(1,2),C(0,2).
将z=3x-y化为y=3x-z,由图知,当直线y=3x-z经过点A(3,0)时,截距-z取得最小值,从而z取得最大值.
zmax=3×3=9.
易错警示 因为目标函数中y的系数为负值,所以容易理解为在点C处取得最大值,导致错误.
28.(2018课标Ⅲ文,15,5分)若变量x,y满足约束条件则z=x+y的最大值是 .
答案 3
解析 本题考查简单的线性规划.
解法一:根据约束条件作出可行域,如图所示.
z=x+y可化为y=-3x+3z.
求z的最大值可转化为求直线y=-3x+3z纵截距的最大值,
显然当直线y=-3x+3z过A(2,3)时,纵截距最大,
故zmax=2+×3=3.
解法二:画出可行域(如上图),由图知可行域为三角形区域,易求得顶点坐标分别为(2,3),(2,-7),(-2,1),将三点坐标代入,可知zmax=2+×3=3.
29.(2018浙江,12,6分)若x,y满足约束条件则z=x+3y的最小值是 ,最大值是 .
答案 -2;8
解析 本小题考查简单的线性规划.
由约束条件得可行域是以A(1,1),B(2,2),C(4,-2)为顶点的三角形区域(含边界),如图.
当直线y=-x+过点C(4,-2)时,z=x+3y取得最小值-2,过点B(2,2)时,z=x+3y取得最大值8.
思路分析 (1)作出可行域,并求出顶点坐标.
(2)平移直线y=-x,当在y轴上的截距最小时,z=x+3y取得最小值,当在y轴上的截距最大时,z=x+3y取得最大值.
30.(2016课标Ⅲ,13,5分)设x,y满足约束条件则z=2x+3y-5的最小值为 .
答案 -10
解析 可行域如图所示(包括边界),直线2x-y+1=0与x-2y-1=0相交于点(-1,-1),当目标函数线过(-1,-1)时,z取最小值,zmin=-10.
31.(2014安徽,13,5分)不等式组表示的平面区域的面积为 .
答案 4
解析 不等式组表示的平面区域为如图所示的阴影部分.
由得
∴A(0,2),B(2,0),C(8,-2).
直线x+2y-4=0与x轴的交点D的坐标为(4,0).
因此S△ABC=S△ABD+S△BCD=×2×2+×2×2=4.故答案为4.
32.(2013课标Ⅰ,14,5分,0.660)设x,y满足约束条件则z=2x-y的最大值为 .
答案 3
解析 可行域为如图所示的阴影部分,
由z=2x-y,得y=2x-z.-z的几何意义是直线y=2x-z在y轴上的截距,要使z最大,则-z最小,所以当直线y=2x-z过点A(3,3)时,z最大,最大值为2×3-3=3.
33.(2012课标理,14,5分)设x,y满足约束条件则z=x-2y的取值范围为 .
答案 [-3,3]
解析 由不等式组画出可行域(如图所示).
当直线x-2y-z=0过点B(1,2)时,zmin=-3;
过点A(3,0)时,zmax=3.
∴z=x-2y的取值范围是[-3,3].
评析 本题考查了简单线性规划知识;考查了数形结合的思想方法.
34.(2011课标文,14,5分)若变量x,y满足约束条件则z=x+2y的最小值为 .
答案 -6
解析 画出约束条件所表示的平面区域,如图阴影部分所示:
当目标函数表示的直线经过点A(4,-5)时,z有最小值,zmin=4+2×(-5)=-6.
失分警示 本题易将平面区域画错或者将目标函数表示的直线的斜率看成而致错.
评析 本题考查线性规划问题,正确作图是得分的前提.
35.(2023全国甲理,14,5分,易)若x,y满足约束条件则z=3x+2y的最大值为 .
答案 15
解析 画出不等式组所表示的平面区域,如图中阴影部分.
作出直线l0:3x+2y=0,平移直线l0,当直线经过点A时,z取得最大值,由得即A(3,3).故zmax=3×3+2×3=15.
36.(2023全国乙理,14,5分,易)若x,y满足约束条件则z=2x-y的最大值为 .
答案 8
解析 根据题意作出不等式组所表示的平面区域,
由目标函数z=2x-y,可得y=2x-z,
平移直线y=2x,可知过点A时,z有最大值,
联立得所以zmax=2×5-2=8.
37.(2023全国甲文,15,5分,易)若x,y满足约束条件则z=3x+2y的最大值为 .
答案 15
解析 画出不等式组所表示的平面区域,如图中阴影部分.
作出直线l0:3x+2y=0,平移直线l0,当直线经过点A时,z取得最大值,由得即A(3,3).故zmax=3×3+2×3=15.
38.(2023全国乙文,15,5分,中)若x,y满足约束条件则z=2x-y的最大值为 .
答案 8
解析 根据题意作出不等式组所表示的平面区域,
由目标函数z=2x-y,可得y=2x-z,
平移直线y=2x,可知过点A时,z有最大值,
联立得所以zmax=2×5-2=8.
(
第
1
页共
15
页
)
7.2 简单的线性规划
考点 简单的线性规划
1.(2018天津理,2文,2,5分)设变量x,y满足约束条件则目标函数z=3x+5y的最大值为( )
A.6 B.19 C.21 D.45
答案 C 本题主要考查线性目标函数最值的求解.
由变量x,y满足的约束条件画出可行域(如图阴影部分所示).
作出基本直线l0:3x+5y=0,平移直线l0,当经过点A(2,3)时,z取最大值,zmax=3×2+5×3=21,故选C.
2.(2018北京理,8,5分)设集合A={(x,y)|x-y≥1,ax+y>4,x-ay≤2},则( )
A.对任意实数a,(2,1)∈A
B.对任意实数a,(2,1) A
C.当且仅当a<0时,(2,1) A
D.当且仅当a≤时,(2,1) A
答案 D 本题主要考查不等式组的解法,元素与集合的关系.
若(2,1)∈A,则有解得a>.结合四个选项,只有D说法正确.故选D.
易错警示 注意区分集合条件中的“或”与“且”.本题容易把三个不等式的中间联结词认为是“或”而错选A.
3.(2017课标Ⅲ文,5,5分)设x,y满足约束条件则z=x-y的取值范围是( )
A.[-3,0] B.[-3,2] C.[0,2] D.[0,3]
答案 B 由题意,画出可行域(如图中阴影部分所示),易知A(0,3),B(2,0).
由图可知,目标函数z=x-y在点A,B处分别取得最小值与最大值,zmin=0-3=-3,zmax=2-0=2,
故z=x-y的取值范围是[-3,2].故选B.
4.(2017课标Ⅰ文,7,5分)设x,y满足约束条件则z=x+y的最大值为( )
A.0 B.1 C.2 D.3
答案 D 本题考查简单的线性规划问题.
作出约束条件表示的可行域如图:
平移直线x+y=0,可得目标函数z=x+y在A(3,0)处取得最大值,zmax=3,故选D.
一题多解 由约束条件求出三个交点的坐标(3,0),(1,0),,分别代入目标函数z=x+y,得到zmax=3.
5.(2016北京理,2,5分)若x,y满足则2x+y的最大值为 ( )
A.0 B.3 C.4 D.5
答案 C 画出可行域,如图中阴影部分所示,令z=2x+y,则y=-2x+z,当直线y=-2x+z过点A(1,2)时,z最大,zmax=4.故选C.
思路分析 先画出可行域,再令z=2x+y并改写成斜截式,找到令z取最大值时的点,代入求值.
评析 本题考查简单的线性规划,属容易题.
6.(2016天津理,2,5分)设变量x,y满足约束条件则目标函数z=2x+5y的最小值为( )
A.-4 B.6 C.10 D.17
答案 B 由线性约束条件画出可行域(如图中阴影部分).
当直线2x+5y-z=0过点A(3,0)时,zmin=2×3+5×0=6,故选B.
评析 本题考查了简单的线性规划问题,正确画出可行域是求解的关键.
7.(2016山东,4,5分)若变量x,y满足则x2+y2的最大值是( )
A.4 B.9 C.10 D.12
答案 C 作出不等式组所表示的平面区域,如图(阴影部分)所示,
x2+y2表示平面区域内的点到原点的距离的平方,由图易知平面区域内的点A(3,-1)到原点的距离最大,所以x2+y2的最大值是10,故选C.
评析 本题考查了数形结合的思想方法.利用x2+y2的几何意义是求解的关键.
8.(2016浙江,4,5分)若平面区域夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是( )
A. B. C. D.
答案 B 作出可行域如图.
由得A(2,1),
由得B(1,2).
斜率为1的平行直线l1,l2分别过A,B两点时它们之间的距离最小.过A(2,1)的直线l1:y=x-1,过B(1,2)的直线l2:y=x+1,此时两平行直线间的距离d==.故选B.
9.(2015重庆,10,5分)若不等式组表示的平面区域为三角形,且其面积等于,则m的值为( )
A.-3 B.1 C. D.3
答案 B 如图,要使不等式组表示的平面区域为三角形,则-2m<2,即m>-1,所围成的区域为△ABC,S△ABC=S△ADC-S△BDC.
点A的纵坐标为1+m,点B的纵坐标为(1+m),C,D两点的横坐标分别为2,-2m,
所以S△ABC=(2+2m)(1+m)-(2+2m)·(1+m)
=(1+m)2=,
解得m=-3(舍去)或m=1.
故选B.
10.(2015山东理,6,5分)已知x,y满足约束条件若z=ax+y的最大值为4,则a=( )
A.3 B.2 C.-2 D.-3
答案 B 作出可行域如图.
①当a<0时,显然z=ax+y的最大值不为4;②当a=0时,z=y在B(1,1)处取得最大值,为1,不符合题意;③当0
11.(2015福建文,10,5分)变量x,y满足约束条件若z=2x-y的最大值为2,则实数m等于( )
A.-2 B.-1 C.1 D.2
答案 C 当m<0时,约束条件所表示的平面区域是开放的,目标函数z=2x-y无最大值,排除A,B,当m=2时,目标函数z=2x-y的最大值为0,于是排除D,故选C.
12.(2014课标Ⅱ理,9,5分,0.798)设x,y满足约束条件则z=2x-y的最大值为( )
A.10 B.8 C.3 D.2
答案 B 由约束条件得可行域如图阴影部分所示.
由得A(5,2).当直线2x-y=z过点A时,z=2x-y取得最大值.其最大值为2×5-2=8.故选B.
方法总结 解决线性规划问题的一般步骤:①画出可行域;②根据目标函数的几何意义确定其取得最优解的点,并求出该点坐标;③求出目标函数的最大值或最小值.
13.(2014课标Ⅱ文,9,5分,0.700)设x,y满足约束条件则z=x+2y的最大值为( )
A.8 B.7
C.2 D.1
答案 B 约束条件表示的平面区域如图中阴影部分所示,
由z=x+2y,得y=-x+,为直线y=-x+在y轴上的截距,要使z最大,则需最大,所以当直线y=-x+经过点B(3,2)时,z最大,最大值为3+2×2=7,故选B.
14.(2014课标Ⅰ文,11,5分,0.236)设x,y满足约束条件且z=x+ay的最小值为7,则a=( )
A.-5 B.3
C.-5或3 D.5或-3
答案 B 二元一次不等式组表示的平面区域如图所示,其中A.平移直线x+ay=0,可知在点A处,z取得最值,
因此+a×=7,化简得a2+2a-15=0,
解得a=3或a=-5,但a=-5时,z取得最大值,故舍去,故选B.
解后反思 本题也可由排除法选出答案,当a=-5时,目标函数无最小值,当a=3时,可以判断出目标函数的最小值为7,所以选B.
15.(2014北京理,6,5分)若x,y满足且z=y-x的最小值为-4,则k的值为( )
A.2 B.-2 C. D.-
答案 D 由得A(4,0).
由图推测直线kx-y+2=0必过A(4,0),得k=-,经验证符合题目条件.故选D.
16.(2014课标Ⅰ理,9,5分)不等式组的解集记为D.有下面四个命题:
p1: (x,y)∈D,x+2y≥-2,
p2: (x,y)∈D,x+2y≥2,
p3: (x,y)∈D,x+2y≤3,
p4: (x,y)∈D,x+2y≤-1.
其中的真命题是( )
A.p2,p3 B.p1,p2 C.p1,p4 D.p1,p3
答案 B 不等式组表示的平面区域D如图阴影区域所示.设z=x+2y,作出基本直线l0:x+2y=0,经平移可知直线l:z=x+2y经过点A(2,-1)时z取得最小值0,无最大值.对于命题p1:由于z的最小值为0,所以 (x,y)∈D,x+2y≥0恒成立,故x+2y≥-2恒成立,因此命题p1为真命题;由于 (x,y)∈D,x+2y≥0,故 (x,y)∈D,x+2y≥2,因此命题p2为真命题;由于z=x+2y的最小值为0,无最大值,故命题p3与p4错误,故选B.
17.(2013课标Ⅱ文,3,5分,0.693)设x,y满足约束条件则z=2x-3y的最小值是( )
A.-7 B.-6 C.-5 D.-3
答案 B 由约束条件得可行域(如图),当直线2x-3y-z=0过点A(3,4)时,zmin=2×3-3×4=-6.故选B.
18.(2013课标Ⅱ理,9,5分,0.788)已知a>0,x,y满足约束条件若z=2x+y的最小值为1,则a=( )
A. B. C.1 D.2
答案 B 由约束条件画出可行域(如图所示的△ABC及其内部),
由得A(1,-2a),
当直线2x+y-z=0过点A时,z=2x+y取得最小值,所以1=2×1-2a,解得a=,故选B.
解题关键 根据约束条件准确画出可行域,从而经过平移确定直线z=2x+y过可行域内的点A时z取得最小值是解题的关键.
19.(2013湖北文,9,5分)某旅行社租用A、B两种型号的客车安排900名客人旅行,A、B两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆.则租金最少为 ( )
A.31200元 B.36000元 C.36800元 D.38400元
答案 C 设旅行社租用A型客车x辆,B型客车y辆,租金为z元,则线性约束条件为目标函数为z=1600x+2400y.
画出可行域:
当目标函数z=1600x+2400y经过点A(5,12)时,zmin=1600×5+2400×12=36800.选C.
20.(2012课标,5,5分)已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是( )
A.(1-,2) B.(0,2)
C.(-1,2) D.(0,1+)
答案 A 由题意知可行域为△ABC(不含边界).
当直线-x+y-z=0过点C(1+,2)时,zmin=1-;当过点B(1,3)时,zmax=2.故选A.
评析 本题考查了简单的线性规划,考查了数形结合的思想.正确理解直线的斜率、截距的几何意义是求解的关键.
21.(2016浙江,3,5分)在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域中的点在直线x+y-2=0上的投影构成的线段记为AB,则|AB|=( )
A.2 B.4 C.3 D.6
答案 C 由不等式组画出可行域,如图中的阴影部分所示.因为直线x+y-2=0与直线x+y=0平行,所以可行域内的点在直线x+y-2=0上的投影构成的线段的长|AB|即为|CD|.易得C(2,-2),D(-1,1),所以|AB|=|CD|==3.故选C.
22.(2022全国乙文,5,5分)若x,y满足约束条件则z=2x-y的最大值是 ( )
A.-2 B.4 C.8 D.12
答案 C 由约束条件作出可行域如图中阴影部分所示,
联立可得A(4,0),
当直线z=2x-y过点A时,z=2x-y取最大值,
zmax=2×4-0=8,故选C.
23.(2021全国乙文,5,5分)若x,y满足约束条件则z=3x+y的最小值为 ( )
A.18 B.10 C.6 D.4
答案 C 解题指导:思路一:先画出可行域,然后移动直线3x+y=0,最后由z与纵截距的关系得最优解,计算即可;
思路二:先求出可行域顶点的坐标,然后分别求出各顶点处目标函数值,通过比较大小得到z的最小值.
解析 解法一:作出不等式组表示的可行域,如图.
作直线l:3x+y=0,平行移动直线l,可知当平移后的直线过点(1,3)时,纵截距最小,即z最小.故zmin=3×1+3=6.故选C.
解法二:根据线性约束条件得出可行域为△ABC及其内部(如上图所示),其中A(3,1),B(1,3),C(5,3),经检验,知目标直线过点B(1,3)时,z取最小值,即zmin=3×1+3=6.
解后反思:对于直线z=Ax+By,若B>0,则当目标直线向上移动时,z变大;若B<0,则当目标直线向下移动时,z变大.
24.(2020课标Ⅰ理,13,5分)若x,y满足约束条件则z=x+7y的最大值为 .
答案 1
审题指导:作出可行域移动直线x+7y=0过A(1,0)时有zmax.
解题思路:作出可行域如图,由z=x+7y得y=-,易知当直线y=-经过点A(1,0)时,z取得最大值,zmax=1+7×0=1.
方法总结:线性规划问题的最优解一般在可行域的边界或顶点处取得,所以可以通过平移目标函数所对应的直线判断最优解,还可以通过比较边界或顶点处的目标函数值进行判断.
25.(2016江苏,12,5分)已知实数x,y满足则x2+y2的取值范围是 .
答案
解析 画出不等式组表示的可行域如图:
由x-2y+4=0及3x-y-3=0得A(2,3),由x2+y2表示可行域内的点(x,y)与点(0,0)的距离的平方可得(x2+y2)max=22+32=13,(x2+y2)min=d2==,其中d表示点(0,0)到直线2x+y-2=0的距离,所以x2+y2的取值范围为.
解后反思 对于线性规划问题,要正确作出可行域,并理解目标函数的几何意义,分清常规的“距离型”“斜率型”与“截距型”是解题的关键.
26.(2020课标Ⅱ文,15,5分)若x,y满足约束条件则z=x+2y的最大值是 .
答案 8
解析 作出约束条件表示的可行域,如图所示.由图可知直线z=x+2y过点A(2,3)时,z取得最大值,最大值为2+2×3=8.
27.(2019课标Ⅱ文,13,5分)若变量x,y满足约束条件则z=3x-y的最大值是 .
答案 9
解析 本题考查简单的线性规划问题;以二元一次不等式组作为约束条件考查学生数形结合思想及运算求解能力;考查数学运算的核心素养.
作出可行域(如图阴影部分所示).
易得A(3,0),B(1,2),C(0,2).
将z=3x-y化为y=3x-z,由图知,当直线y=3x-z经过点A(3,0)时,截距-z取得最小值,从而z取得最大值.
zmax=3×3=9.
易错警示 因为目标函数中y的系数为负值,所以容易理解为在点C处取得最大值,导致错误.
28.(2018课标Ⅲ文,15,5分)若变量x,y满足约束条件则z=x+y的最大值是 .
答案 3
解析 本题考查简单的线性规划.
解法一:根据约束条件作出可行域,如图所示.
z=x+y可化为y=-3x+3z.
求z的最大值可转化为求直线y=-3x+3z纵截距的最大值,
显然当直线y=-3x+3z过A(2,3)时,纵截距最大,
故zmax=2+×3=3.
解法二:画出可行域(如上图),由图知可行域为三角形区域,易求得顶点坐标分别为(2,3),(2,-7),(-2,1),将三点坐标代入,可知zmax=2+×3=3.
29.(2018浙江,12,6分)若x,y满足约束条件则z=x+3y的最小值是 ,最大值是 .
答案 -2;8
解析 本小题考查简单的线性规划.
由约束条件得可行域是以A(1,1),B(2,2),C(4,-2)为顶点的三角形区域(含边界),如图.
当直线y=-x+过点C(4,-2)时,z=x+3y取得最小值-2,过点B(2,2)时,z=x+3y取得最大值8.
思路分析 (1)作出可行域,并求出顶点坐标.
(2)平移直线y=-x,当在y轴上的截距最小时,z=x+3y取得最小值,当在y轴上的截距最大时,z=x+3y取得最大值.
30.(2016课标Ⅲ,13,5分)设x,y满足约束条件则z=2x+3y-5的最小值为 .
答案 -10
解析 可行域如图所示(包括边界),直线2x-y+1=0与x-2y-1=0相交于点(-1,-1),当目标函数线过(-1,-1)时,z取最小值,zmin=-10.
31.(2014安徽,13,5分)不等式组表示的平面区域的面积为 .
答案 4
解析 不等式组表示的平面区域为如图所示的阴影部分.
由得
∴A(0,2),B(2,0),C(8,-2).
直线x+2y-4=0与x轴的交点D的坐标为(4,0).
因此S△ABC=S△ABD+S△BCD=×2×2+×2×2=4.故答案为4.
32.(2013课标Ⅰ,14,5分,0.660)设x,y满足约束条件则z=2x-y的最大值为 .
答案 3
解析 可行域为如图所示的阴影部分,
由z=2x-y,得y=2x-z.-z的几何意义是直线y=2x-z在y轴上的截距,要使z最大,则-z最小,所以当直线y=2x-z过点A(3,3)时,z最大,最大值为2×3-3=3.
33.(2012课标理,14,5分)设x,y满足约束条件则z=x-2y的取值范围为 .
答案 [-3,3]
解析 由不等式组画出可行域(如图所示).
当直线x-2y-z=0过点B(1,2)时,zmin=-3;
过点A(3,0)时,zmax=3.
∴z=x-2y的取值范围是[-3,3].
评析 本题考查了简单线性规划知识;考查了数形结合的思想方法.
34.(2011课标文,14,5分)若变量x,y满足约束条件则z=x+2y的最小值为 .
答案 -6
解析 画出约束条件所表示的平面区域,如图阴影部分所示:
当目标函数表示的直线经过点A(4,-5)时,z有最小值,zmin=4+2×(-5)=-6.
失分警示 本题易将平面区域画错或者将目标函数表示的直线的斜率看成而致错.
评析 本题考查线性规划问题,正确作图是得分的前提.
35.(2023全国甲理,14,5分,易)若x,y满足约束条件则z=3x+2y的最大值为 .
答案 15
解析 画出不等式组所表示的平面区域,如图中阴影部分.
作出直线l0:3x+2y=0,平移直线l0,当直线经过点A时,z取得最大值,由得即A(3,3).故zmax=3×3+2×3=15.
36.(2023全国乙理,14,5分,易)若x,y满足约束条件则z=2x-y的最大值为 .
答案 8
解析 根据题意作出不等式组所表示的平面区域,
由目标函数z=2x-y,可得y=2x-z,
平移直线y=2x,可知过点A时,z有最大值,
联立得所以zmax=2×5-2=8.
37.(2023全国甲文,15,5分,易)若x,y满足约束条件则z=3x+2y的最大值为 .
答案 15
解析 画出不等式组所表示的平面区域,如图中阴影部分.
作出直线l0:3x+2y=0,平移直线l0,当直线经过点A时,z取得最大值,由得即A(3,3).故zmax=3×3+2×3=15.
38.(2023全国乙文,15,5分,中)若x,y满足约束条件则z=2x-y的最大值为 .
答案 8
解析 根据题意作出不等式组所表示的平面区域,
由目标函数z=2x-y,可得y=2x-z,
平移直线y=2x,可知过点A时,z有最大值,
联立得所以zmax=2×5-2=8.
(
第
1
页共
15
页
)
同课章节目录
