2014-2023年高考数学真题专题分类--8.2 直线、平面平行的判定与性质(含解析)
文档属性
| 名称 | 2014-2023年高考数学真题专题分类--8.2 直线、平面平行的判定与性质(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 17:18:53 | ||
图片预览




文档简介
2014-2023年高考数学真题专题分类
8.3 直线、平面平行的判定与性质
考点 直线、平面平行的判定与性质
1.(2011辽宁理,8,5分)如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
答案 D ∵四边形ABCD是正方形,∴AC⊥BD.
又∵SD⊥底面ABCD,∴SD⊥AC.
其中SD∩BD=D,∴AC⊥面SDB,从而AC⊥SB.故A正确.易知B正确.
设AC与DB交于O点,连接SO.
则SA与平面SBD所成的角为∠ASO,SC与平面SBD所成的角为∠CSO,
又OA=OC,SA=SC,∴∠ASO=∠CSO.故C正确.
由排除法可知选D.
评析 本题主要考查了线面平行与垂直的判断及线面角、线线角的概念.属中档题.
2.(2023全国甲理,15,5分,中)在正方体ABCD-A1B1C1D1中,E,F分别为AB,C1D1的中点.以EF为直径的球的球面与该正方体的棱共有 个公共点.
答案 12
解析 设正方体的棱长为2,则EF=2,所以以EF为直径的球的半径为,球心为正方体的中心O,由于正方体的中心O到正方体各棱的距离均为,所以正方体各棱的中点都在球面上,并且为各棱与球的唯一交点,所以以EF为直径的球的球面与该正方体的棱共有12个公共点.
3.(2023全国乙文,16,5分,中)已知点S,A,B,C均在半径为2的球面上,△ABC是边长为3的等边三角形,SA⊥平面ABC,则SA= .
答案 2
解析 由题意知△ABC的外接圆半径r满足2r=,则r=,
如图,O为球心,O1为△ABC外接圆的圆心,连接OS,OA,OO1,AO1,易得OO1⊥平面ABC,作OM⊥SA交SA于点M,由OA=OS得MA=SA,
又因为SA⊥平面ABC,所以OO1=MA=SA,
所以+r2=22,
所以SA=2.
4.(2021浙江,6,4分)如图,已知正方体ABCD-A1B1C1D1,M,N分别是A1D,D1B的中点,则 ( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
答案 A 解题指导:利用线面平行的判定定理和线面垂直的判定定理解决此类问题.
解析 连接AD1,在正方形ADD1A1中,
由M为A1D的中点,可知AD1∩A1D=M,且M为AD1的中点,AD1⊥A1D.
又∵N为D1B的中点,∴MN∥AB.
∵AB 平面ABCD,MN 平面ABCD,∴MN∥平面ABCD.
∵AB⊥平面ADD1A1,A1D 平面ADD1A1,∴AB⊥A1D,
∵AB∩AD1=A,∴A1D⊥平面ABD1,
∴A1D⊥D1B.故A正确.
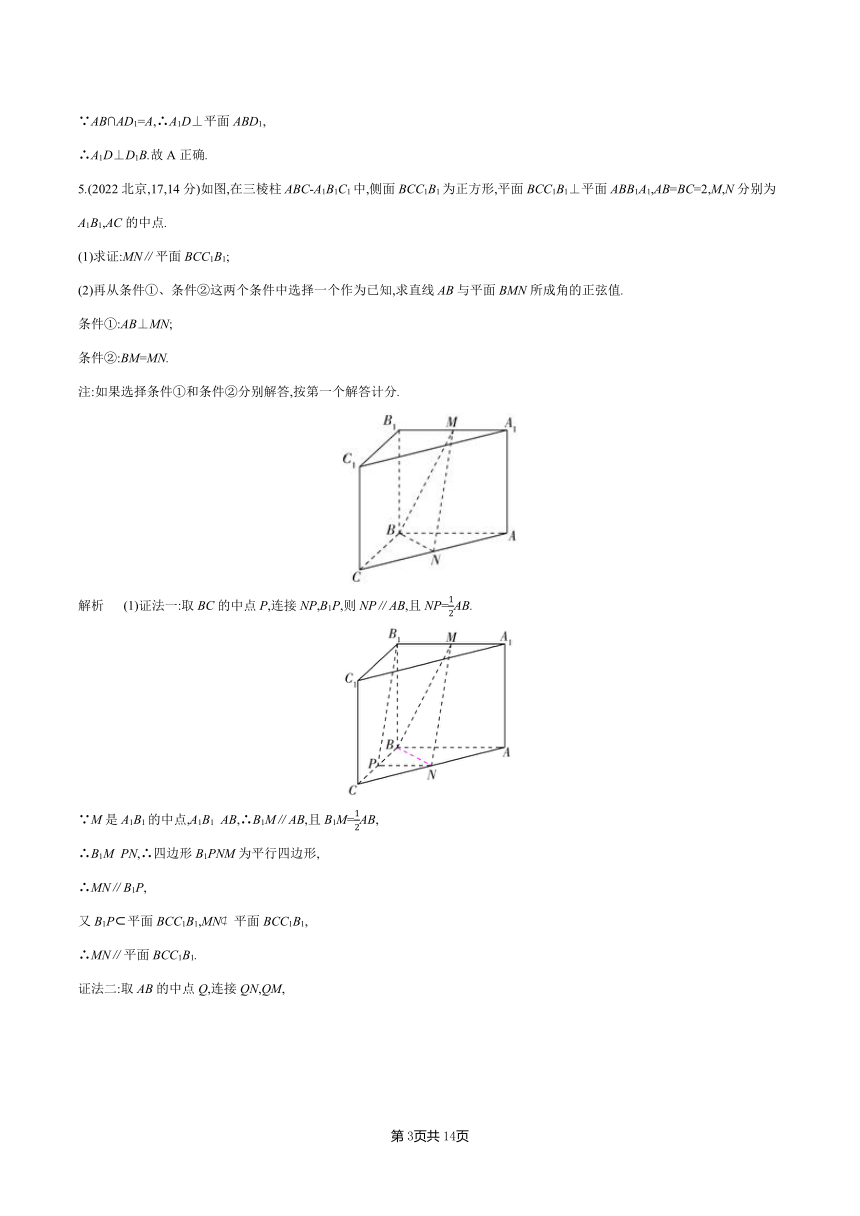
5.(2022北京,17,14分)如图,在三棱柱ABC-A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.
(1)求证:MN∥平面BCC1B1;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:AB⊥MN;
条件②:BM=MN.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
解析 (1)证法一:取BC的中点P,连接NP,B1P,则NP∥AB,且NP=AB.
∵M是A1B1的中点,A1B1 AB,∴B1M∥AB,且B1M=AB,
∴B1M PN,∴四边形B1PNM为平行四边形,
∴MN∥B1P,
又B1P 平面BCC1B1,MN 平面BCC1B1,
∴MN∥平面BCC1B1.
证法二:取AB的中点Q,连接QN,QM,
∵M,N分别是A1B1,AC的中点,
∴QN∥BC,QM∥B1B,
∵QN 平面BCC1B1,BC 平面BCC1B1,
∴QN∥平面BCC1B1,同理,QM∥平面BCC1B1,
又QM∩QN=Q,∴平面MNQ∥平面BCC1B1,
又MN 平面MNQ,∴MN∥平面BCC1B1.
(2)选择条件①.
∵侧面BCC1B1为正方形,∴BC⊥BB1,又平面BCC1B1⊥平面ABB1A1,平面BCC1B1∩平面ABB1A1=BB1,BC 平面BCC1B1,∴BC⊥平面ABB1A1,∴BC⊥AB.
解法一:由(1)中证法一知MN∥B1P,又AB⊥MN,∴AB⊥B1P.
∵BC∩B1P=P,∴AB⊥平面BCC1B1.∴AB⊥BB1.
∴BC,B1B,BA两两垂直.
以B为原点,建立如图所示的空间直角坐标系,
则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2),
∴=(0,1,2),=(1,1,0),=(0,-2,0).
设平面BMN的法向量为n=(x,y,z),
则令z=1,得n=(2,-2,1).
∴cos故直线AB与平面BMN所成角的正弦值为.
解法二:连接MA.
易知NQ⊥AB,又AB⊥MN,MN∩NQ=N,∴AB⊥平面MNQ,∴AB⊥MQ.
结合(1)中证法二知NQ⊥MQ.又AB∩NQ=Q,
∴MQ⊥平面ABN,∴点M到平面ABN的距离为2.
∴V三棱锥M-ABN=.
易知BM=,BN=,MN=,
∴S△BMN=.
设A到平面BMN的距离为h,
则VA-BMN=VM-ABN=,
即,∴h=,
∴直线AB与平面BMN所成角的正弦值为.
选择条件②.
∵侧面BCC1B1为正方形,∴BC⊥BB1,又平面BCC1B1⊥平面ABB1A1,平面BCC1B1∩平面ABB1A1=BB1,BC 平面BCC1B1,∴BC⊥平面ABB1A1,∴BC⊥AB.
结合(1)中证法二易知MQ⊥NQ.∵AB=BC=2,∴NQ=BQ=1.又BM=MN,MQ=MQ,∴△MBQ≌△MNQ,
∴MQ⊥BQ.∴BB1,BC,BA两两垂直.
解法一(向量法):同选①的解法一.
解法二(几何法):同选①的解法二.
6.(2019课标Ⅰ文,19,12分)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
解析 本题考查了线面平行、垂直的判定和点到平面的距离,通过平行、垂直的证明,考查了学生的空间想象力,体现了直观想象的核心素养.
(1)连接B1C,ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME=B1C.又因为N为A1D的中点,所以ND=A1D.
由题设知A1B1 DC,可得B1C A1D,故ME ND,因此四边形MNDE为平行四边形,MN∥ED.
又MN 平面C1DE,所以MN∥平面C1DE.
(2)过C作C1E的垂线,垂足为H.
由已知可得DE⊥BC,DE⊥C1C,所以DE⊥平面C1CE,
故DE⊥CH.
从而CH⊥平面C1DE,
故CH的长即为C到平面C1DE的距离.
由已知可得CE=1,C1C=4,所以C1E=,
故CH=.
从而点C到平面C1DE的距离为.
思路分析 (1)连接B1C,ME.证明四边形MNDE是平行四边形,得出MN∥DE,然后利用线面平行的判定定理证出结论.(2)注意到DE⊥平面BCC1B1,只需过点C作C1E的垂线便可求解.
7.(2017课标Ⅱ文,18,12分)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.
(1)证明:直线BC∥平面PAD;
(2)若△PCD的面积为2,求四棱锥P-ABCD的体积.
解析 本题考查线面平行的判定和体积的计算.
(1)证明:在平面ABCD内,
因为∠BAD=∠ABC=90°,
所以BC∥AD.
又BC 平面PAD,AD 平面PAD,故BC∥平面PAD.
(2)取AD的中点M,连接PM,CM.
由AB=BC=AD及BC∥AD,∠ABC=90°得四边形ABCM为正方形,则CM⊥AD.
因为侧面PAD为等边三角形且垂直于底面ABCD,平面PAD∩平面ABCD=AD,所以PM⊥AD,PM⊥底面ABCD.
因为CM 底面ABCD,
所以PM⊥CM.
设BC=x,则CM=x,CD=x,PM=x,PC=PD=2x.
取CD的中点N,连接PN,
则PN⊥CD,所以PN=x.
因为△PCD的面积为2,
所以×x×x=2,
解得x=-2(舍去)或x=2.于是AB=BC=2,AD=4,PM=2.
所以四棱锥P-ABCD的体积V=××2=4.
8.(2016课标Ⅲ文,19,12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明MN∥平面PAB;
(2)求四面体N-BCM的体积.
解析 (1)证明:由已知得AM=AD=2,
取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.(3分)
又AD∥BC,故TN AM,故四边形AMNT为平行四边形,于是MN∥AT.
因为AT 平面PAB,MN 平面PAB,所以MN∥平面PAB.(6分)
(2)因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为PA.(9分)
取BC的中点E,连接AE.
由AB=AC=3得AE⊥BC,AE==.
由AM∥BC得M到BC的距离为,
故S△BCM=×4×=2.
所以四面体N-BCM的体积VN-BCM=·S△BCM·=.(12分)
评析 本题考查了线面平行的判定,考查了三棱锥的体积,考查了空间想象能力.线段的中点问题一般应用三角形的中位线求解.
9.(2014课标Ⅱ文,18,12分)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=,三棱锥P-ABD的体积V=,求A到平面PBC的距离.
解析 (1)证明:设BD与AC的交点为O,连接EO.
因为ABCD为矩形,
所以O为BD的中点.
又E为PD的中点,
所以EO∥PB.
EO 平面AEC,PB 平面AEC,
所以PB∥平面AEC.
(2)V=PA·AB·AD=AB.
又V=,
所以AB=,
所以PB==.
作AH⊥PB交PB于H.
由题设知BC⊥平面PAB,
因为AH 平面PAB,
所以BC⊥AH,
又BC∩BP=B,
故AH⊥平面PBC.
又AH==,
所以A到平面PBC的距离为.
思路分析 (1)由线线平行证出线面平行;
(2)首先由题设求出AB,然后过A作AH⊥PB于H,证明AH就是A到平面PBC的距离,通过解三角形求解即可.
10.(2014安徽,19,13分)如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
(1)证明:GH∥EF;
(2)若EB=2,求四边形GEFH的面积.
解析 (1)证明:因为BC∥平面GEFH,BC 平面PBC,且平面PBC∩平面GEFH=GH,所以GH∥BC.
同理可证EF∥BC,
因此GH∥EF.
(2)连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.
又BD∩AC=O,且AC,BD都在底面内,所以PO⊥底面ABCD.又因为平面GEFH⊥平面ABCD,且PO 平面GEFH,
所以PO∥平面GEFH.
因为平面PBD∩平面GEFH=GK,
所以PO∥GK,且GK⊥底面ABCD,
从而GK⊥EF.
所以GK是梯形GEFH的高.
由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,
从而KB=DB=OB,即K为OB的中点.
再由PO∥GK得GK=PO,即G是PB的中点,且GH=BC=4.
由已知可得OB=4,PO===6,
所以GK=3.
故四边形GEFH的面积S=·GK=×3=18.
评析 本题考查线面平行与垂直关系的转化,同时考查空间想象能力和逻辑推理能力,解题时要有较强的分析问题、解决问题的能力.
11.(2013课标Ⅱ文,18,12分)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2,求三棱锥C-A1DE的体积.
解析 (1)证明:连接AC1交A1C于点F,
则F为AC1中点.
由D是AB中点,连接DF,则BC1∥DF.
因为DF 平面A1CD,BC1 平面A1CD,
所以BC1∥平面A1CD.
(2)因为ABC-A1B1C1是直三棱柱,
所以AA1⊥CD.由已知AC=CB,D为AB的中点,
所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2得
∠ACB=90°,CD=,A1D=,DE=,A1E=3,
故A1D2+DE2=A1E2,即DE⊥A1D.
所以=××××=1.
思路分析 (1)利用线面平行的判定定理在平面A1CD内找出一条直线与直线BC1平行即可;
(2)先证明CD⊥平面ABB1A1,再根据题目给的条件算出三棱锥C-A1DE的高和底面面积,利用三棱锥的体积公式计算即可.
一题多解 证明第(1)问时,也可以利用面面平行的性质,即:取A1B1的中点G,连接C1G,GB,因为GB∥A1D,C1G∥CD,C1G 平面GBC1,GB 平面GBC1,且C1G∩GB=G,A1D 平面A1CD,CD 平面A1CD,A1D∩CD=D,所以平面GBC1∥平面A1CD.又BC1 平面GBC1,所以BC1∥平面A1CD.
12.(2011北京文,17,14分)如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
(1)求证:DE∥平面BCP;
(2)求证:四边形DEFG为矩形;
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等 说明理由.
解析 (1)证明:因为D,E分别为AP,AC的中点,所以DE∥PC.又因为DE 平面BCP,PC 平面BCP,
所以DE∥平面BCP.
(2)证明:因为D,E,F,G分别为AP,AC,BC,PB的中点,所以DE∥PC∥FG,DG∥AB∥EF.
所以四边形DEFG为平行四边形.又因为PC⊥AB,
所以DE⊥DG.所以四边形DEFG为矩形.
(3)存在点Q满足条件.理由如下:
连接DF,EG,设Q为EG的中点.
由(2)知,DF∩EG=Q,且QD=QE=QF=QG=EG.
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN.
与(2)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,且QM=QN=EG,所以Q为满足条件的点.
13.(2015课标Ⅱ文,19,12分)如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求平面α把该长方体分成的两部分体积的比值.
解析 (1)交线围成的正方形EHGF如图:
(2)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.
因为EHGF为正方形,所以EH=EF=BC=10.
于是MH==6,AH=10,HB=6.
因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为.
14.(2023全国甲文,18,12分,中)如图,在三棱柱ABC-A1B1C1中,A1C⊥平面ABC,∠ACB=90°.
(1)证明:平面ACC1A1⊥平面BB1C1C;
(2)设AB=A1B,AA1=2,求四棱锥A1-BB1C1C的高.
解析 (1)证明:∵A1C⊥平面ABC,BC 平面ABC,
∴A1C⊥BC.∵∠ACB=90°,∴AC⊥BC,
又∵A1C,AC 平面ACC1A1,且A1C∩AC=C,
∴BC⊥平面ACC1A1,又∵BC 平面BB1C1C,
∴平面ACC1A1⊥平面BB1C1C.
(2)过A1作A1O⊥CC1,垂足为O,
∵平面ACC1A1⊥平面BB1C1C,且平面ACC1A1∩平面BB1C1C=CC1,A1O 平面ACC1A1,
∴A1O⊥平面BB1C1C,即A1O是四棱锥A1-BB1C1C的高.
由(1)知∠A1CB=∠BCA=90°.
在Rt△A1CB与Rt△ACB中,A1B=AB,BC=BC,
∴Rt△A1CB≌Rt△ACB,∴A1C=AC,∴A1C=A1C1,
又知A1C⊥A1C1,
∴△CA1C1为等腰直角三角形,∴A1O=CC1=AA1=1,即四棱锥A1-BB1C1C的高为1.
(
第
1
页共
14
页
)
8.3 直线、平面平行的判定与性质
考点 直线、平面平行的判定与性质
1.(2011辽宁理,8,5分)如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
答案 D ∵四边形ABCD是正方形,∴AC⊥BD.
又∵SD⊥底面ABCD,∴SD⊥AC.
其中SD∩BD=D,∴AC⊥面SDB,从而AC⊥SB.故A正确.易知B正确.
设AC与DB交于O点,连接SO.
则SA与平面SBD所成的角为∠ASO,SC与平面SBD所成的角为∠CSO,
又OA=OC,SA=SC,∴∠ASO=∠CSO.故C正确.
由排除法可知选D.
评析 本题主要考查了线面平行与垂直的判断及线面角、线线角的概念.属中档题.
2.(2023全国甲理,15,5分,中)在正方体ABCD-A1B1C1D1中,E,F分别为AB,C1D1的中点.以EF为直径的球的球面与该正方体的棱共有 个公共点.
答案 12
解析 设正方体的棱长为2,则EF=2,所以以EF为直径的球的半径为,球心为正方体的中心O,由于正方体的中心O到正方体各棱的距离均为,所以正方体各棱的中点都在球面上,并且为各棱与球的唯一交点,所以以EF为直径的球的球面与该正方体的棱共有12个公共点.
3.(2023全国乙文,16,5分,中)已知点S,A,B,C均在半径为2的球面上,△ABC是边长为3的等边三角形,SA⊥平面ABC,则SA= .
答案 2
解析 由题意知△ABC的外接圆半径r满足2r=,则r=,
如图,O为球心,O1为△ABC外接圆的圆心,连接OS,OA,OO1,AO1,易得OO1⊥平面ABC,作OM⊥SA交SA于点M,由OA=OS得MA=SA,
又因为SA⊥平面ABC,所以OO1=MA=SA,
所以+r2=22,
所以SA=2.
4.(2021浙江,6,4分)如图,已知正方体ABCD-A1B1C1D1,M,N分别是A1D,D1B的中点,则 ( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
答案 A 解题指导:利用线面平行的判定定理和线面垂直的判定定理解决此类问题.
解析 连接AD1,在正方形ADD1A1中,
由M为A1D的中点,可知AD1∩A1D=M,且M为AD1的中点,AD1⊥A1D.
又∵N为D1B的中点,∴MN∥AB.
∵AB 平面ABCD,MN 平面ABCD,∴MN∥平面ABCD.
∵AB⊥平面ADD1A1,A1D 平面ADD1A1,∴AB⊥A1D,
∵AB∩AD1=A,∴A1D⊥平面ABD1,
∴A1D⊥D1B.故A正确.
5.(2022北京,17,14分)如图,在三棱柱ABC-A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.
(1)求证:MN∥平面BCC1B1;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:AB⊥MN;
条件②:BM=MN.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
解析 (1)证法一:取BC的中点P,连接NP,B1P,则NP∥AB,且NP=AB.
∵M是A1B1的中点,A1B1 AB,∴B1M∥AB,且B1M=AB,
∴B1M PN,∴四边形B1PNM为平行四边形,
∴MN∥B1P,
又B1P 平面BCC1B1,MN 平面BCC1B1,
∴MN∥平面BCC1B1.
证法二:取AB的中点Q,连接QN,QM,
∵M,N分别是A1B1,AC的中点,
∴QN∥BC,QM∥B1B,
∵QN 平面BCC1B1,BC 平面BCC1B1,
∴QN∥平面BCC1B1,同理,QM∥平面BCC1B1,
又QM∩QN=Q,∴平面MNQ∥平面BCC1B1,
又MN 平面MNQ,∴MN∥平面BCC1B1.
(2)选择条件①.
∵侧面BCC1B1为正方形,∴BC⊥BB1,又平面BCC1B1⊥平面ABB1A1,平面BCC1B1∩平面ABB1A1=BB1,BC 平面BCC1B1,∴BC⊥平面ABB1A1,∴BC⊥AB.
解法一:由(1)中证法一知MN∥B1P,又AB⊥MN,∴AB⊥B1P.
∵BC∩B1P=P,∴AB⊥平面BCC1B1.∴AB⊥BB1.
∴BC,B1B,BA两两垂直.
以B为原点,建立如图所示的空间直角坐标系,
则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2),
∴=(0,1,2),=(1,1,0),=(0,-2,0).
设平面BMN的法向量为n=(x,y,z),
则令z=1,得n=(2,-2,1).
∴cos
解法二:连接MA.
易知NQ⊥AB,又AB⊥MN,MN∩NQ=N,∴AB⊥平面MNQ,∴AB⊥MQ.
结合(1)中证法二知NQ⊥MQ.又AB∩NQ=Q,
∴MQ⊥平面ABN,∴点M到平面ABN的距离为2.
∴V三棱锥M-ABN=.
易知BM=,BN=,MN=,
∴S△BMN=.
设A到平面BMN的距离为h,
则VA-BMN=VM-ABN=,
即,∴h=,
∴直线AB与平面BMN所成角的正弦值为.
选择条件②.
∵侧面BCC1B1为正方形,∴BC⊥BB1,又平面BCC1B1⊥平面ABB1A1,平面BCC1B1∩平面ABB1A1=BB1,BC 平面BCC1B1,∴BC⊥平面ABB1A1,∴BC⊥AB.
结合(1)中证法二易知MQ⊥NQ.∵AB=BC=2,∴NQ=BQ=1.又BM=MN,MQ=MQ,∴△MBQ≌△MNQ,
∴MQ⊥BQ.∴BB1,BC,BA两两垂直.
解法一(向量法):同选①的解法一.
解法二(几何法):同选①的解法二.
6.(2019课标Ⅰ文,19,12分)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
解析 本题考查了线面平行、垂直的判定和点到平面的距离,通过平行、垂直的证明,考查了学生的空间想象力,体现了直观想象的核心素养.
(1)连接B1C,ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME=B1C.又因为N为A1D的中点,所以ND=A1D.
由题设知A1B1 DC,可得B1C A1D,故ME ND,因此四边形MNDE为平行四边形,MN∥ED.
又MN 平面C1DE,所以MN∥平面C1DE.
(2)过C作C1E的垂线,垂足为H.
由已知可得DE⊥BC,DE⊥C1C,所以DE⊥平面C1CE,
故DE⊥CH.
从而CH⊥平面C1DE,
故CH的长即为C到平面C1DE的距离.
由已知可得CE=1,C1C=4,所以C1E=,
故CH=.
从而点C到平面C1DE的距离为.
思路分析 (1)连接B1C,ME.证明四边形MNDE是平行四边形,得出MN∥DE,然后利用线面平行的判定定理证出结论.(2)注意到DE⊥平面BCC1B1,只需过点C作C1E的垂线便可求解.
7.(2017课标Ⅱ文,18,12分)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.
(1)证明:直线BC∥平面PAD;
(2)若△PCD的面积为2,求四棱锥P-ABCD的体积.
解析 本题考查线面平行的判定和体积的计算.
(1)证明:在平面ABCD内,
因为∠BAD=∠ABC=90°,
所以BC∥AD.
又BC 平面PAD,AD 平面PAD,故BC∥平面PAD.
(2)取AD的中点M,连接PM,CM.
由AB=BC=AD及BC∥AD,∠ABC=90°得四边形ABCM为正方形,则CM⊥AD.
因为侧面PAD为等边三角形且垂直于底面ABCD,平面PAD∩平面ABCD=AD,所以PM⊥AD,PM⊥底面ABCD.
因为CM 底面ABCD,
所以PM⊥CM.
设BC=x,则CM=x,CD=x,PM=x,PC=PD=2x.
取CD的中点N,连接PN,
则PN⊥CD,所以PN=x.
因为△PCD的面积为2,
所以×x×x=2,
解得x=-2(舍去)或x=2.于是AB=BC=2,AD=4,PM=2.
所以四棱锥P-ABCD的体积V=××2=4.
8.(2016课标Ⅲ文,19,12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明MN∥平面PAB;
(2)求四面体N-BCM的体积.
解析 (1)证明:由已知得AM=AD=2,
取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.(3分)
又AD∥BC,故TN AM,故四边形AMNT为平行四边形,于是MN∥AT.
因为AT 平面PAB,MN 平面PAB,所以MN∥平面PAB.(6分)
(2)因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为PA.(9分)
取BC的中点E,连接AE.
由AB=AC=3得AE⊥BC,AE==.
由AM∥BC得M到BC的距离为,
故S△BCM=×4×=2.
所以四面体N-BCM的体积VN-BCM=·S△BCM·=.(12分)
评析 本题考查了线面平行的判定,考查了三棱锥的体积,考查了空间想象能力.线段的中点问题一般应用三角形的中位线求解.
9.(2014课标Ⅱ文,18,12分)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=,三棱锥P-ABD的体积V=,求A到平面PBC的距离.
解析 (1)证明:设BD与AC的交点为O,连接EO.
因为ABCD为矩形,
所以O为BD的中点.
又E为PD的中点,
所以EO∥PB.
EO 平面AEC,PB 平面AEC,
所以PB∥平面AEC.
(2)V=PA·AB·AD=AB.
又V=,
所以AB=,
所以PB==.
作AH⊥PB交PB于H.
由题设知BC⊥平面PAB,
因为AH 平面PAB,
所以BC⊥AH,
又BC∩BP=B,
故AH⊥平面PBC.
又AH==,
所以A到平面PBC的距离为.
思路分析 (1)由线线平行证出线面平行;
(2)首先由题设求出AB,然后过A作AH⊥PB于H,证明AH就是A到平面PBC的距离,通过解三角形求解即可.
10.(2014安徽,19,13分)如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
(1)证明:GH∥EF;
(2)若EB=2,求四边形GEFH的面积.
解析 (1)证明:因为BC∥平面GEFH,BC 平面PBC,且平面PBC∩平面GEFH=GH,所以GH∥BC.
同理可证EF∥BC,
因此GH∥EF.
(2)连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.
又BD∩AC=O,且AC,BD都在底面内,所以PO⊥底面ABCD.又因为平面GEFH⊥平面ABCD,且PO 平面GEFH,
所以PO∥平面GEFH.
因为平面PBD∩平面GEFH=GK,
所以PO∥GK,且GK⊥底面ABCD,
从而GK⊥EF.
所以GK是梯形GEFH的高.
由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,
从而KB=DB=OB,即K为OB的中点.
再由PO∥GK得GK=PO,即G是PB的中点,且GH=BC=4.
由已知可得OB=4,PO===6,
所以GK=3.
故四边形GEFH的面积S=·GK=×3=18.
评析 本题考查线面平行与垂直关系的转化,同时考查空间想象能力和逻辑推理能力,解题时要有较强的分析问题、解决问题的能力.
11.(2013课标Ⅱ文,18,12分)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2,求三棱锥C-A1DE的体积.
解析 (1)证明:连接AC1交A1C于点F,
则F为AC1中点.
由D是AB中点,连接DF,则BC1∥DF.
因为DF 平面A1CD,BC1 平面A1CD,
所以BC1∥平面A1CD.
(2)因为ABC-A1B1C1是直三棱柱,
所以AA1⊥CD.由已知AC=CB,D为AB的中点,
所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2得
∠ACB=90°,CD=,A1D=,DE=,A1E=3,
故A1D2+DE2=A1E2,即DE⊥A1D.
所以=××××=1.
思路分析 (1)利用线面平行的判定定理在平面A1CD内找出一条直线与直线BC1平行即可;
(2)先证明CD⊥平面ABB1A1,再根据题目给的条件算出三棱锥C-A1DE的高和底面面积,利用三棱锥的体积公式计算即可.
一题多解 证明第(1)问时,也可以利用面面平行的性质,即:取A1B1的中点G,连接C1G,GB,因为GB∥A1D,C1G∥CD,C1G 平面GBC1,GB 平面GBC1,且C1G∩GB=G,A1D 平面A1CD,CD 平面A1CD,A1D∩CD=D,所以平面GBC1∥平面A1CD.又BC1 平面GBC1,所以BC1∥平面A1CD.
12.(2011北京文,17,14分)如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
(1)求证:DE∥平面BCP;
(2)求证:四边形DEFG为矩形;
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等 说明理由.
解析 (1)证明:因为D,E分别为AP,AC的中点,所以DE∥PC.又因为DE 平面BCP,PC 平面BCP,
所以DE∥平面BCP.
(2)证明:因为D,E,F,G分别为AP,AC,BC,PB的中点,所以DE∥PC∥FG,DG∥AB∥EF.
所以四边形DEFG为平行四边形.又因为PC⊥AB,
所以DE⊥DG.所以四边形DEFG为矩形.
(3)存在点Q满足条件.理由如下:
连接DF,EG,设Q为EG的中点.
由(2)知,DF∩EG=Q,且QD=QE=QF=QG=EG.
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN.
与(2)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,且QM=QN=EG,所以Q为满足条件的点.
13.(2015课标Ⅱ文,19,12分)如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求平面α把该长方体分成的两部分体积的比值.
解析 (1)交线围成的正方形EHGF如图:
(2)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.
因为EHGF为正方形,所以EH=EF=BC=10.
于是MH==6,AH=10,HB=6.
因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为.
14.(2023全国甲文,18,12分,中)如图,在三棱柱ABC-A1B1C1中,A1C⊥平面ABC,∠ACB=90°.
(1)证明:平面ACC1A1⊥平面BB1C1C;
(2)设AB=A1B,AA1=2,求四棱锥A1-BB1C1C的高.
解析 (1)证明:∵A1C⊥平面ABC,BC 平面ABC,
∴A1C⊥BC.∵∠ACB=90°,∴AC⊥BC,
又∵A1C,AC 平面ACC1A1,且A1C∩AC=C,
∴BC⊥平面ACC1A1,又∵BC 平面BB1C1C,
∴平面ACC1A1⊥平面BB1C1C.
(2)过A1作A1O⊥CC1,垂足为O,
∵平面ACC1A1⊥平面BB1C1C,且平面ACC1A1∩平面BB1C1C=CC1,A1O 平面ACC1A1,
∴A1O⊥平面BB1C1C,即A1O是四棱锥A1-BB1C1C的高.
由(1)知∠A1CB=∠BCA=90°.
在Rt△A1CB与Rt△ACB中,A1B=AB,BC=BC,
∴Rt△A1CB≌Rt△ACB,∴A1C=AC,∴A1C=A1C1,
又知A1C⊥A1C1,
∴△CA1C1为等腰直角三角形,∴A1O=CC1=AA1=1,即四棱锥A1-BB1C1C的高为1.
(
第
1
页共
14
页
)
同课章节目录
