2014-2023年高考数学真题专题分类--专题十五 不等式选讲(含解析)
文档属性
| 名称 | 2014-2023年高考数学真题专题分类--专题十五 不等式选讲(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 277.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 09:46:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2014-2023年高考数学真题专题分类
专题十五 不等式选讲
考点一 绝对值不等式
1.(2018课标Ⅱ文,23,10分)[选修4—5:不等式选讲]
设函数f(x)=5-|x+a|-|x-2|.
(1)当a=1时,求不等式f(x)≥0的解集;
(2)若f(x)≤1,求a的取值范围.
解析 (1)当a=1时,f(x)=
可得f(x)≥0的解集为{x|-2≤x≤3}.
(2)f(x)≤1等价于|x+a|+|x-2|≥4.
而|x+a|+|x-2|≥|a+2|,且当x=2时等号成立.
故f(x)≤1等价于|a+2|≥4.
由|a+2|≥4可得a≤-6或a≥2.
所以a的取值范围是(-∞,-6]∪[2,+∞).
方法总结 解含有两个或两个以上绝对值的不等式,常用零点分段法或数形结合法;若函数中含有两个或两个以上的绝对值,在求函数最值时,常用绝对值三角不等式或数形结合法求解.
2.(2017课标Ⅲ理,23,10分)已知函数f(x)=|x+1|-|x-2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.
解析 本题考查绝对值不等式的解法.
(1)f(x)=
当x<-1时,f(x)≥1无解;
当-1≤x≤2时,由f(x)≥1得,2x-1≥1,解得1≤x≤2;
当x>2时,由f(x)≥1解得x>2.
所以f(x)≥1的解集为{x|x≥1}.
(2)由f(x)≥x2-x+m得m≤|x+1|-|x-2|-x2+x.
而|x+1|-|x-2|-x2+x≤|x|+1+|x|-2-x2+|x|
=-+≤,
且当x=时,|x+1|-|x-2|-x2+x=.
故m的取值范围为.
思路分析 (1)分段讨论,求得符合题意的x的取值范围,最后取并集.(2)不等式的解集非空,即不等式能成立,转化为求函数的最值处理.
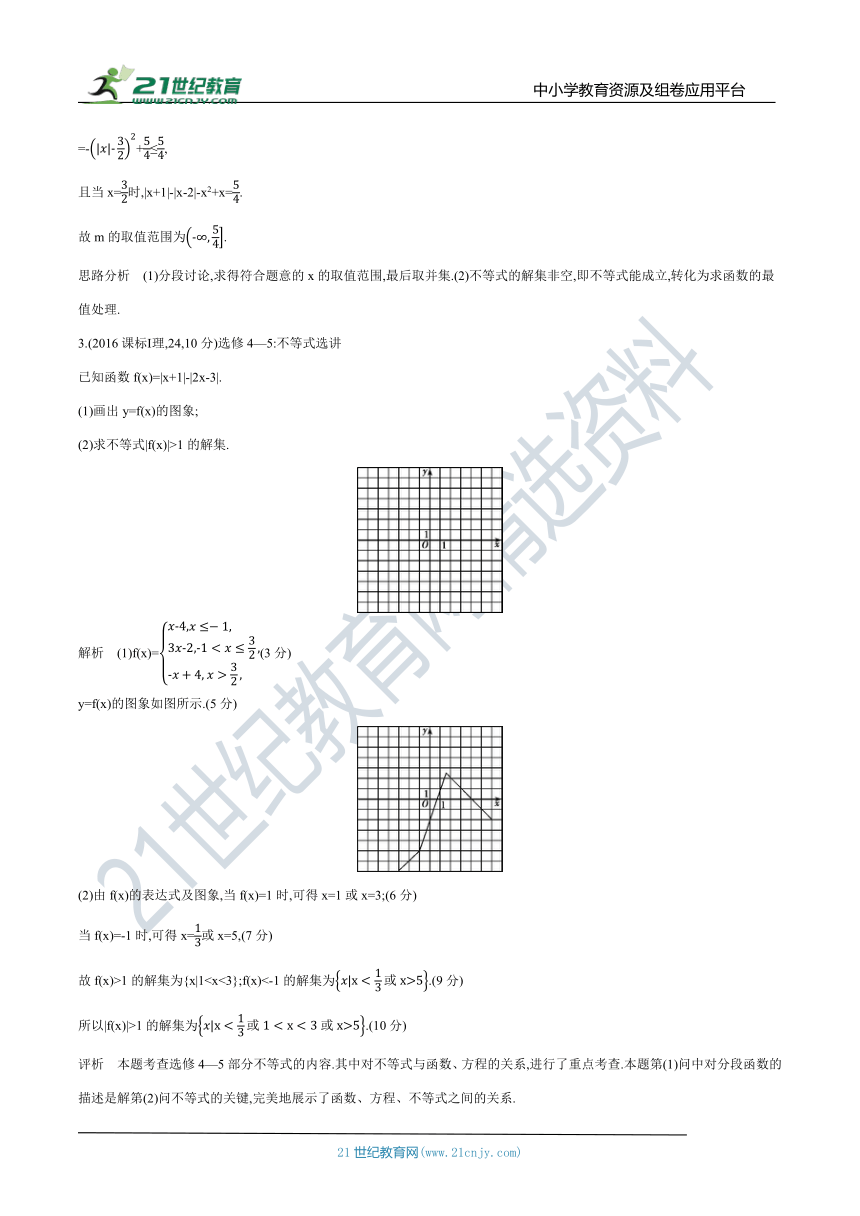
3.(2016课标Ⅰ理,24,10分)选修4—5:不等式选讲
已知函数f(x)=|x+1|-|2x-3|.
(1)画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
解析 (1)f(x)=(3分)
y=f(x)的图象如图所示.(5分)
(2)由f(x)的表达式及图象,当f(x)=1时,可得x=1或x=3;(6分)
当f(x)=-1时,可得x=或x=5,(7分)
故f(x)>1的解集为{x|1所以|f(x)|>1的解集为.(10分)
评析 本题考查选修4—5部分不等式的内容.其中对不等式与函数、方程的关系,进行了重点考查.本题第(1)问中对分段函数的描述是解第(2)问不等式的关键,完美地展示了函数、方程、不等式之间的关系.
4.(2016课标Ⅲ理,24,10分)已知函数f(x)=|2x-a|+a.
(1)当a=2时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x-1|.当x∈R时,f(x)+g(x)≥3,求a的取值范围.
解析 (1)当a=2时,f(x)=|2x-2|+2.
解不等式|2x-2|+2≤6得-1≤x≤3.
因此f(x)≤6的解集为{x|-1≤x≤3}.(5分)
(2)当x∈R时,
f(x)+g(x)=|2x-a|+a+|1-2x|≥|2x-a+1-2x|+a=|1-a|+a,
当x=时等号成立,所以当x∈R时,f(x)+g(x)≥3等价于|1-a|+a≥3.①(7分)
当a≤1时,①等价于1-a+a≥3,无解.
当a>1时,①等价于a-1+a≥3,解得a≥2.
所以a的取值范围是[2,+∞).(10分)
方法总结 (1)解含一个绝对值不等式利用|m(x)|≤n -n≤m(x)≤n求解即可;
(2)解决f(x)+g(x)≥3恒成立,只需f(x)+g(x)的最小值≥3即可,利用|x|+|y|≥|x±y|来求最值即可.
评析 本题主要考查了绝对值不等式的解法及不等式恒成立问题,要f(x)+g(x)≥3恒成立,只需f(x)+g(x)的最小值≥3即可.
5.(2015课标Ⅰ理,24,10分)选修4—5:不等式选讲
已知函数f(x)=|x+1|-2|x-a|,a>0.
(1)当a=1时,求不等式f(x)>1的解集;
(2)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
解析 (1)当a=1时,f(x)>1化为|x+1|-2|x-1|-1>0.
当x≤-1时,不等式化为x-4>0,无解;
当-10,解得当x≥1时,不等式化为-x+2>0,解得1≤x<2.
所以f(x)>1的解集为.
(2)由题设可得,f(x)=
所以函数f(x)的图象与x轴围成的三角形的三个顶点分别为A,B(2a+1,0),C(a,a+1),△ABC的面积为(a+1)2.
由题设得(a+1)2>6,故a>2.
所以a的取值范围为(2,+∞).
6.(2014课标Ⅱ理,24,10分)选修4—5:不等式选讲
设函数f(x)=+|x-a|(a>0).
(1)证明:f(x)≥2;
(2)若f(3)<5,求a的取值范围.
解析 (1)证明:由a>0,得f(x)=+|x-a|≥=+a≥2.
所以f(x)≥2.
(2)f(3)=+|3-a|.
当a>3时,f(3)=a+,由f(3)<5得3当0综上,a的取值范围是.
评析 本题考查了含绝对值不等式的解法,考查了分类讨论思想.
7.(2014辽宁,24,10分)选修4—5:不等式选讲
设函数f(x)=2|x-1|+x-1,g(x)=16x2-8x+1,记f(x)≤1的解集为M,g(x)≤4的解集为N.
(1)求M;
(2)当x∈M∩N时,证明:x2f(x)+x[f(x)]2≤.
解析 (1)f(x)=
当x≥1时,由f(x)=3x-3≤1得x≤,故1≤x≤;
当x<1时,由f(x)=1-x≤1得x≥0,故0≤x<1.
所以f(x)≤1的解集为M=.
(2)证明:由g(x)=16x2-8x+1≤4得16≤4,
解得-≤x≤.
因此N=,故M∩N=.
当x∈M∩N时,f(x)=1-x,于是x2f(x)+x·[f(x)]2
=xf(x)[x+f(x)]=x·f(x)=x(1-x)=-≤.
8.(2013课标Ⅰ理,24,10分)选修4—5:不等式选讲
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)(2)设a>-1,且当x∈时,f(x)≤g(x),求a的取值范围.
解析 (1)当a=-2时,不等式f(x)设函数y=|2x-1|+|2x-2|-x-3,则
y=
其图象如图所示.从图象可知,当且仅当x∈(0,2)时,y<0.所以原不等式的解集是{x|0(2)当x∈时,f(x)=1+a.
不等式f(x)≤g(x)化为1+a≤x+3.
所以x≥a-2对x∈都成立.
故-≥a-2,即a≤.
从而a的取值范围是.
9.(2012课标理,24,10分)选修4—5:不等式选讲
已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
解析 (1)当a=-3时,
f(x)=
当x≤2时,由f(x)≥3得-2x+5≥3,解得x≤1;
当2当x≥3时,由f(x)≥3得2x-5≥3,解得x≥4,
所以f(x)≥3的解集为{x|x≤1}∪{x|x≥4}.
(2)f(x)≤|x-4| |x-4|-|x-2|≥|x+a|.
当x∈[1,2]时,|x-4|-|x-2|≥|x+a|
4-x-(2-x)≥|x+a| -2-a≤x≤2-a.
由条件得-2-a≤1且2-a≥2,即-3≤a≤0.
故满足条件的a的取值范围为[-3,0].
评析 本题考查了含绝对值不等式的解法,运用分类讨论解含绝对值的不等式,考查了学生的运算求解能力.
10.(2011课标,24,10分)选修4—5:不等式选讲
设函数f(x)=|x-a|+3x,其中a>0.
(1)当a=1时,求不等式f(x)≥3x+2的解集;
(2)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
解析 (1)当a=1时,f(x)≥3x+2可化为|x-1|≥2.
由此可得x≥3或x≤-1.故不等式f(x)≥3x+2的解集为{x|x≥3或x≤-1}.
(2)由f(x)≤0得|x-a|+3x≤0.
此不等式化为不等式组或
即或
因为a>0,所以不等式组的解集为.
由题设可得-=-1,故a=2.
评析 本题考查绝对值不等式的解法和分类讨论的数学思想方法,属中等难度题.
11.(2021全国甲理,23,10分)已知函数f(x)=|x-2|,g(x)=|2x+3|-|2x-1|.
(1)画出y=f(x)和y=g(x)的图象;
(2)若f(x+a)≥g(x),求a的取值范围.
解题指导:(1)先将含绝对值的函数转化为分段函数,再画图.
(2)先将f(x)的图象平移找到满足f(x+a)≥g(x)的a的临界值,再结合图象确定a的取值范围.
解析 (1)依题意,可得f(x)=
g(x)=
画出f(x)与g(x)的图象,如下:
(2)函数f(x+a)的图象是由f(x)的图象向左或向右平移|a|个单位长度所得,由(1)中图象可知,要使f(x+a)≥g(x),则需要f(x)的图象向左平移a个单位长度,且a>0,当f(x+a)的图象过点时,=4,解得a=,
∴要使f(x+a)≥g(x),则a≥,
∴a的取值范围为.
方法总结:解决含参数的不等式问题常采用数形结合法,由图象确定参数的范围.
12.(2021全国乙文,23,10分)已知函数f(x)=|x-a|+|x+3|.
(1)当a=1时,求不等式f(x)≥6的解集;
(2)若f(x)>-a,求a的取值范围.
解题指导:(1)当a=1时,通过零点分区间化简f(x),然后解不等式组;(2)把f(x)>-a转化为f(x)min>-a来求解.
解析 (1)当a=1时, f(x)=
则f(x)≥6等价于解得x≤-4或x∈ 或x≥2,所以f(x)≥6的解集为(-∞,-4]∪[2,+∞).
(2)f(x)>-a,即为f(x)min>-a,
因为f(x)=|x-a|+|x+3|≥|(x-a)-(x+3)|=|a+3|(当且仅当(x-a)(x+3)≤0时等号成立),所以f(x)min=|a+3|,所以|a+3|>-a,即为a+3-a,解得a∈.
易错警示 ①含绝对值的函数在转化为分段函数过程中易忽略x的取值范围;②在不等式放缩的过程中要注意等号成立的条件.
13.(2020课标Ⅰ理,23,10分)已知函数f(x)=|3x+1|-2|x-1|.
(1)画出y=f(x)的图象;
(2)求不等式f(x)>f(x+1)的解集.
解析 (1)由题设知f(x)=
y=f(x)的图象如图所示.
(2)函数y=f(x)的图象向左平移1个单位长度后得到函数y=f(x+1)的图象.
y=f(x)的图象与y=f(x+1)的图象的交点坐标为.
由图象可知当且仅当x<-时,y=f(x)的图象在y=f(x+1)的图象上方.
故不等式f(x)>f(x+1)的解集为.
14.(2020课标Ⅱ理,23,10分)已知函数f(x)=|x-a2|+|x-2a+1|.
(1)当a=2时,求不等式f(x)≥4的解集;
(2)若f(x)≥4,求a的取值范围.
解析 (1)当a=2时, f(x)=
因此,不等式f(x)≥4的解集为.
(2)因为f(x)=|x-a2|+|x-2a+1|≥|a2-2a+1|=(a-1)2,故当(a-1)2≥4,即|a-1|≥2时, f(x)≥4.所以当a≥3或a≤-1时, f(x)≥4.
当-1所以a的取值范围是(-∞,-1]∪[3,+∞).
15.(2023全国甲理,23,10分,中)设a>0,函数f(x)=2|x-a|-a.
(1)求不等式f(x)(2)若曲线y=f(x)与x轴所围成的图形的面积为2,求a.
解析 (1)依题意, f(x)=
则f(x)解得a≤x<3a或所以f(x)(2)曲线y=f(x)如图所示.
曲线f(x)与x轴围成的图形的面积S=·a=2,即a2=4,又∵a>0,∴a=2.
16.(2023全国乙理,23,10分,中)已知f(x)=2|x|+|x-2|.
(1)求不等式f(x)≤6-x的解集;
(2)在直角坐标系xOy中,求不等式组所确定的平面区域的面积.
解析 (1)f(x)=2|x|+|x-2|=
不等式f(x)≤6-x等价于或或
解得-2≤x≤0或0(2)不等式组等价于f(x)≤6-x,分别作出y=f(x)的图象及直线y=6-x,
∴不等式组所表示的平面区域如图中阴影部分所示(△ABC及其内部).
由解得A(-2,8).
由解得C(2,4),又B(0,2),D(0,6),
∴S△ABC=×4×4=8.
一题多解 (2)由(1)知不等式组可以等价转化为或或
画出上述不等式组所表示的平面区域,如图中阴影部分所示.
其中A(-2,8),B(0,2),C(2,4),D(0,6),
∴所求平面区域的面积S=×4×4=8.
考点二 不等式的证明
1.(2015课标Ⅱ理,24,10分)选修4—5:不等式选讲
设a,b,c,d均为正数,且a+b=c+d,证明:
(1)若ab>cd,则+>+;
(2)+>+是|a-b|<|c-d|的充要条件.
证明 (1)因为(+)2=a+b+2,(+)2=c+d+2,
由题设a+b=c+d,ab>cd得(+)2>(+)2.
因此+>+.
(2)(i)若|a-b|<|c-d|,则(a-b)2<(c-d)2,
即(a+b)2-4ab<(c+d)2-4cd.
因为a+b=c+d,所以ab>cd.
由(1)得+>+.
(ii)若+>+,则(+)2>(+)2,
即a+b+2>c+d+2.
因为a+b=c+d,所以ab>cd.于是
(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.
因此|a-b|<|c-d|.
综上,+>+是|a-b|<|c-d|的充要条件.
2.(2015湖南理,16(3),6分)选修4—5:不等式选讲
设a>0,b>0,且a+b=+.证明:
(1)a+b≥2;
(2)a2+a<2与b2+b<2不可能同时成立.
证明 证明:由a+b=+=,a>0,b>0,得ab=1.
(1)由基本不等式及ab=1,有a+b≥2=2,即a+b≥2.
(2)假设a2+a<2与b2+b<2同时成立,则由a2+a<2及a>0得0评析 本题考查基本不等式的应用、一元二次不等式的解法、反证法等知识.难度不大.
3.(2014课标Ⅰ理,24,10分)选修4—5:不等式选讲
若a>0,b>0,且+=.
(1)求a3+b3的最小值;
(2)是否存在a,b,使得2a+3b=6 并说明理由.
解析 (1)由=+≥,得ab≥2,且当a=b=时等号成立.
故a3+b3≥2≥4,且当a=b=时等号成立.
所以a3+b3的最小值为4.
(2)由(1)知,2a+3b≥2≥4.
由于4>6,从而不存在a,b,使得2a+3b=6.
4.(2013课标Ⅱ理,24,10分)选修4—5:不等式选讲
设a,b,c均为正数,且a+b+c=1,证明:
(1)ab+bc+ca≤;
(2)++≥1.
证明 (1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca得a2+b2+c2≥ab+bc+ca.
由题设得(a+b+c)2=1,
即a2+b2+c2+2ab+2bc+2ca=1.
所以3(ab+bc+ca)≤1,即ab+bc+ca≤.
(2)因为+b≥2a,+c≥2b,+a≥2c,故+++(a+b+c)≥2(a+b+c),即++≥a+b+c.
所以++≥1.
5.(2022全国甲,23,10分)已知a,b,c均为正数,且a2+b2+4c2=3,证明:
(1)a+b+2c≤3;
(2)若b=2c,则≥3.
证明:(1)证法一:由柯西不等式可得[a2+b2+(2c)2](12+12+12)≥(a+b+2c)2,当且仅当a=b=2c时,取“=”,
又∵a2+b2+4c2=3,∴(a+b+2c)2≤9,
又∵a,b,c均为正数,∴a+b+2c≤3.
证法二:∵a2+b2≥2ab,a2+4c2≥4ac,b2+4c2≥4bc,
∴a2+b2+(2c)2≥ab+2ac+2bc,当且仅当a=b=2c时,取“=”.
又∵a2+b2+4c2=3,∴ab+2ac+2bc≤3,
∴(a+b+2c)2=a2+b2+4c2+2(ab+2ac+2bc)=3+2(ab+2ac+2bc)≤9.
又∵a,b,c均为正数,∴a+b+2c≤3.
(2)∵三个正数的算术平均数不小于它们的调和平均数,∴,当且仅当a=b=2c时,取“=”.
由(1)得a+b+2c≤3,
∴≥3,又∵b=2c,∴≥3.
6.(2022全国乙,23,10分)已知a,b,c都是正数,且=1,证明:
(1)abc≤;
(2).
证明 (1)因为a,b,c都是正数,所以1=,当且仅当a=b=c=时取等号,所以3≤1,即abc≤.
(2)证法一:要证成立,只需证,因为b+c≥2,a+c≥2,a+b≥2,当且仅当a=b=c=时取等号,所以.
证法二:因为b+c≥2,
所以(当且仅当b=c时取等号),
同理(当且仅当a=c时取等号),
(当且仅当a=b时取等号),
所以,
当且仅当a=b=c=时取等号.
7.(2020课标Ⅲ理,23,10分)设a,b,c∈R,a+b+c=0,abc=1.
(1)证明:ab+bc+ca<0;
(2)用max{a,b,c}表示a,b,c的最大值,证明:max{a,b,c}≥.
解析 (1)由题设可知,a,b,c均不为零,所以ab+bc+ca=[(a+b+c)2-(a2+b2+c2)]=-(a2+b2+c2)<0.
(2)不妨设max{a,b,c}=a,因为abc=1,a=-(b+c),
所以a>0,b<0,c<0.由bc≤,可得abc≤,
故a≥,所以max{a,b,c}≥.
21世纪教育网(www.21cnjy.com)
2014-2023年高考数学真题专题分类
专题十五 不等式选讲
考点一 绝对值不等式
1.(2018课标Ⅱ文,23,10分)[选修4—5:不等式选讲]
设函数f(x)=5-|x+a|-|x-2|.
(1)当a=1时,求不等式f(x)≥0的解集;
(2)若f(x)≤1,求a的取值范围.
解析 (1)当a=1时,f(x)=
可得f(x)≥0的解集为{x|-2≤x≤3}.
(2)f(x)≤1等价于|x+a|+|x-2|≥4.
而|x+a|+|x-2|≥|a+2|,且当x=2时等号成立.
故f(x)≤1等价于|a+2|≥4.
由|a+2|≥4可得a≤-6或a≥2.
所以a的取值范围是(-∞,-6]∪[2,+∞).
方法总结 解含有两个或两个以上绝对值的不等式,常用零点分段法或数形结合法;若函数中含有两个或两个以上的绝对值,在求函数最值时,常用绝对值三角不等式或数形结合法求解.
2.(2017课标Ⅲ理,23,10分)已知函数f(x)=|x+1|-|x-2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.
解析 本题考查绝对值不等式的解法.
(1)f(x)=
当x<-1时,f(x)≥1无解;
当-1≤x≤2时,由f(x)≥1得,2x-1≥1,解得1≤x≤2;
当x>2时,由f(x)≥1解得x>2.
所以f(x)≥1的解集为{x|x≥1}.
(2)由f(x)≥x2-x+m得m≤|x+1|-|x-2|-x2+x.
而|x+1|-|x-2|-x2+x≤|x|+1+|x|-2-x2+|x|
=-+≤,
且当x=时,|x+1|-|x-2|-x2+x=.
故m的取值范围为.
思路分析 (1)分段讨论,求得符合题意的x的取值范围,最后取并集.(2)不等式的解集非空,即不等式能成立,转化为求函数的最值处理.
3.(2016课标Ⅰ理,24,10分)选修4—5:不等式选讲
已知函数f(x)=|x+1|-|2x-3|.
(1)画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
解析 (1)f(x)=(3分)
y=f(x)的图象如图所示.(5分)
(2)由f(x)的表达式及图象,当f(x)=1时,可得x=1或x=3;(6分)
当f(x)=-1时,可得x=或x=5,(7分)
故f(x)>1的解集为{x|1
评析 本题考查选修4—5部分不等式的内容.其中对不等式与函数、方程的关系,进行了重点考查.本题第(1)问中对分段函数的描述是解第(2)问不等式的关键,完美地展示了函数、方程、不等式之间的关系.
4.(2016课标Ⅲ理,24,10分)已知函数f(x)=|2x-a|+a.
(1)当a=2时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x-1|.当x∈R时,f(x)+g(x)≥3,求a的取值范围.
解析 (1)当a=2时,f(x)=|2x-2|+2.
解不等式|2x-2|+2≤6得-1≤x≤3.
因此f(x)≤6的解集为{x|-1≤x≤3}.(5分)
(2)当x∈R时,
f(x)+g(x)=|2x-a|+a+|1-2x|≥|2x-a+1-2x|+a=|1-a|+a,
当x=时等号成立,所以当x∈R时,f(x)+g(x)≥3等价于|1-a|+a≥3.①(7分)
当a≤1时,①等价于1-a+a≥3,无解.
当a>1时,①等价于a-1+a≥3,解得a≥2.
所以a的取值范围是[2,+∞).(10分)
方法总结 (1)解含一个绝对值不等式利用|m(x)|≤n -n≤m(x)≤n求解即可;
(2)解决f(x)+g(x)≥3恒成立,只需f(x)+g(x)的最小值≥3即可,利用|x|+|y|≥|x±y|来求最值即可.
评析 本题主要考查了绝对值不等式的解法及不等式恒成立问题,要f(x)+g(x)≥3恒成立,只需f(x)+g(x)的最小值≥3即可.
5.(2015课标Ⅰ理,24,10分)选修4—5:不等式选讲
已知函数f(x)=|x+1|-2|x-a|,a>0.
(1)当a=1时,求不等式f(x)>1的解集;
(2)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
解析 (1)当a=1时,f(x)>1化为|x+1|-2|x-1|-1>0.
当x≤-1时,不等式化为x-4>0,无解;
当-1
所以f(x)>1的解集为.
(2)由题设可得,f(x)=
所以函数f(x)的图象与x轴围成的三角形的三个顶点分别为A,B(2a+1,0),C(a,a+1),△ABC的面积为(a+1)2.
由题设得(a+1)2>6,故a>2.
所以a的取值范围为(2,+∞).
6.(2014课标Ⅱ理,24,10分)选修4—5:不等式选讲
设函数f(x)=+|x-a|(a>0).
(1)证明:f(x)≥2;
(2)若f(3)<5,求a的取值范围.
解析 (1)证明:由a>0,得f(x)=+|x-a|≥=+a≥2.
所以f(x)≥2.
(2)f(3)=+|3-a|.
当a>3时,f(3)=a+,由f(3)<5得3
评析 本题考查了含绝对值不等式的解法,考查了分类讨论思想.
7.(2014辽宁,24,10分)选修4—5:不等式选讲
设函数f(x)=2|x-1|+x-1,g(x)=16x2-8x+1,记f(x)≤1的解集为M,g(x)≤4的解集为N.
(1)求M;
(2)当x∈M∩N时,证明:x2f(x)+x[f(x)]2≤.
解析 (1)f(x)=
当x≥1时,由f(x)=3x-3≤1得x≤,故1≤x≤;
当x<1时,由f(x)=1-x≤1得x≥0,故0≤x<1.
所以f(x)≤1的解集为M=.
(2)证明:由g(x)=16x2-8x+1≤4得16≤4,
解得-≤x≤.
因此N=,故M∩N=.
当x∈M∩N时,f(x)=1-x,于是x2f(x)+x·[f(x)]2
=xf(x)[x+f(x)]=x·f(x)=x(1-x)=-≤.
8.(2013课标Ⅰ理,24,10分)选修4—5:不等式选讲
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)
解析 (1)当a=-2时,不等式f(x)
y=
其图象如图所示.从图象可知,当且仅当x∈(0,2)时,y<0.所以原不等式的解集是{x|0
不等式f(x)≤g(x)化为1+a≤x+3.
所以x≥a-2对x∈都成立.
故-≥a-2,即a≤.
从而a的取值范围是.
9.(2012课标理,24,10分)选修4—5:不等式选讲
已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
解析 (1)当a=-3时,
f(x)=
当x≤2时,由f(x)≥3得-2x+5≥3,解得x≤1;
当2
所以f(x)≥3的解集为{x|x≤1}∪{x|x≥4}.
(2)f(x)≤|x-4| |x-4|-|x-2|≥|x+a|.
当x∈[1,2]时,|x-4|-|x-2|≥|x+a|
4-x-(2-x)≥|x+a| -2-a≤x≤2-a.
由条件得-2-a≤1且2-a≥2,即-3≤a≤0.
故满足条件的a的取值范围为[-3,0].
评析 本题考查了含绝对值不等式的解法,运用分类讨论解含绝对值的不等式,考查了学生的运算求解能力.
10.(2011课标,24,10分)选修4—5:不等式选讲
设函数f(x)=|x-a|+3x,其中a>0.
(1)当a=1时,求不等式f(x)≥3x+2的解集;
(2)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
解析 (1)当a=1时,f(x)≥3x+2可化为|x-1|≥2.
由此可得x≥3或x≤-1.故不等式f(x)≥3x+2的解集为{x|x≥3或x≤-1}.
(2)由f(x)≤0得|x-a|+3x≤0.
此不等式化为不等式组或
即或
因为a>0,所以不等式组的解集为.
由题设可得-=-1,故a=2.
评析 本题考查绝对值不等式的解法和分类讨论的数学思想方法,属中等难度题.
11.(2021全国甲理,23,10分)已知函数f(x)=|x-2|,g(x)=|2x+3|-|2x-1|.
(1)画出y=f(x)和y=g(x)的图象;
(2)若f(x+a)≥g(x),求a的取值范围.
解题指导:(1)先将含绝对值的函数转化为分段函数,再画图.
(2)先将f(x)的图象平移找到满足f(x+a)≥g(x)的a的临界值,再结合图象确定a的取值范围.
解析 (1)依题意,可得f(x)=
g(x)=
画出f(x)与g(x)的图象,如下:
(2)函数f(x+a)的图象是由f(x)的图象向左或向右平移|a|个单位长度所得,由(1)中图象可知,要使f(x+a)≥g(x),则需要f(x)的图象向左平移a个单位长度,且a>0,当f(x+a)的图象过点时,=4,解得a=,
∴要使f(x+a)≥g(x),则a≥,
∴a的取值范围为.
方法总结:解决含参数的不等式问题常采用数形结合法,由图象确定参数的范围.
12.(2021全国乙文,23,10分)已知函数f(x)=|x-a|+|x+3|.
(1)当a=1时,求不等式f(x)≥6的解集;
(2)若f(x)>-a,求a的取值范围.
解题指导:(1)当a=1时,通过零点分区间化简f(x),然后解不等式组;(2)把f(x)>-a转化为f(x)min>-a来求解.
解析 (1)当a=1时, f(x)=
则f(x)≥6等价于解得x≤-4或x∈ 或x≥2,所以f(x)≥6的解集为(-∞,-4]∪[2,+∞).
(2)f(x)>-a,即为f(x)min>-a,
因为f(x)=|x-a|+|x+3|≥|(x-a)-(x+3)|=|a+3|(当且仅当(x-a)(x+3)≤0时等号成立),所以f(x)min=|a+3|,所以|a+3|>-a,即为a+3
易错警示 ①含绝对值的函数在转化为分段函数过程中易忽略x的取值范围;②在不等式放缩的过程中要注意等号成立的条件.
13.(2020课标Ⅰ理,23,10分)已知函数f(x)=|3x+1|-2|x-1|.
(1)画出y=f(x)的图象;
(2)求不等式f(x)>f(x+1)的解集.
解析 (1)由题设知f(x)=
y=f(x)的图象如图所示.
(2)函数y=f(x)的图象向左平移1个单位长度后得到函数y=f(x+1)的图象.
y=f(x)的图象与y=f(x+1)的图象的交点坐标为.
由图象可知当且仅当x<-时,y=f(x)的图象在y=f(x+1)的图象上方.
故不等式f(x)>f(x+1)的解集为.
14.(2020课标Ⅱ理,23,10分)已知函数f(x)=|x-a2|+|x-2a+1|.
(1)当a=2时,求不等式f(x)≥4的解集;
(2)若f(x)≥4,求a的取值范围.
解析 (1)当a=2时, f(x)=
因此,不等式f(x)≥4的解集为.
(2)因为f(x)=|x-a2|+|x-2a+1|≥|a2-2a+1|=(a-1)2,故当(a-1)2≥4,即|a-1|≥2时, f(x)≥4.所以当a≥3或a≤-1时, f(x)≥4.
当-1
15.(2023全国甲理,23,10分,中)设a>0,函数f(x)=2|x-a|-a.
(1)求不等式f(x)
解析 (1)依题意, f(x)=
则f(x)
曲线f(x)与x轴围成的图形的面积S=·a=2,即a2=4,又∵a>0,∴a=2.
16.(2023全国乙理,23,10分,中)已知f(x)=2|x|+|x-2|.
(1)求不等式f(x)≤6-x的解集;
(2)在直角坐标系xOy中,求不等式组所确定的平面区域的面积.
解析 (1)f(x)=2|x|+|x-2|=
不等式f(x)≤6-x等价于或或
解得-2≤x≤0或0
∴不等式组所表示的平面区域如图中阴影部分所示(△ABC及其内部).
由解得A(-2,8).
由解得C(2,4),又B(0,2),D(0,6),
∴S△ABC=×4×4=8.
一题多解 (2)由(1)知不等式组可以等价转化为或或
画出上述不等式组所表示的平面区域,如图中阴影部分所示.
其中A(-2,8),B(0,2),C(2,4),D(0,6),
∴所求平面区域的面积S=×4×4=8.
考点二 不等式的证明
1.(2015课标Ⅱ理,24,10分)选修4—5:不等式选讲
设a,b,c,d均为正数,且a+b=c+d,证明:
(1)若ab>cd,则+>+;
(2)+>+是|a-b|<|c-d|的充要条件.
证明 (1)因为(+)2=a+b+2,(+)2=c+d+2,
由题设a+b=c+d,ab>cd得(+)2>(+)2.
因此+>+.
(2)(i)若|a-b|<|c-d|,则(a-b)2<(c-d)2,
即(a+b)2-4ab<(c+d)2-4cd.
因为a+b=c+d,所以ab>cd.
由(1)得+>+.
(ii)若+>+,则(+)2>(+)2,
即a+b+2>c+d+2.
因为a+b=c+d,所以ab>cd.于是
(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.
因此|a-b|<|c-d|.
综上,+>+是|a-b|<|c-d|的充要条件.
2.(2015湖南理,16(3),6分)选修4—5:不等式选讲
设a>0,b>0,且a+b=+.证明:
(1)a+b≥2;
(2)a2+a<2与b2+b<2不可能同时成立.
证明 证明:由a+b=+=,a>0,b>0,得ab=1.
(1)由基本不等式及ab=1,有a+b≥2=2,即a+b≥2.
(2)假设a2+a<2与b2+b<2同时成立,则由a2+a<2及a>0得0
3.(2014课标Ⅰ理,24,10分)选修4—5:不等式选讲
若a>0,b>0,且+=.
(1)求a3+b3的最小值;
(2)是否存在a,b,使得2a+3b=6 并说明理由.
解析 (1)由=+≥,得ab≥2,且当a=b=时等号成立.
故a3+b3≥2≥4,且当a=b=时等号成立.
所以a3+b3的最小值为4.
(2)由(1)知,2a+3b≥2≥4.
由于4>6,从而不存在a,b,使得2a+3b=6.
4.(2013课标Ⅱ理,24,10分)选修4—5:不等式选讲
设a,b,c均为正数,且a+b+c=1,证明:
(1)ab+bc+ca≤;
(2)++≥1.
证明 (1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca得a2+b2+c2≥ab+bc+ca.
由题设得(a+b+c)2=1,
即a2+b2+c2+2ab+2bc+2ca=1.
所以3(ab+bc+ca)≤1,即ab+bc+ca≤.
(2)因为+b≥2a,+c≥2b,+a≥2c,故+++(a+b+c)≥2(a+b+c),即++≥a+b+c.
所以++≥1.
5.(2022全国甲,23,10分)已知a,b,c均为正数,且a2+b2+4c2=3,证明:
(1)a+b+2c≤3;
(2)若b=2c,则≥3.
证明:(1)证法一:由柯西不等式可得[a2+b2+(2c)2](12+12+12)≥(a+b+2c)2,当且仅当a=b=2c时,取“=”,
又∵a2+b2+4c2=3,∴(a+b+2c)2≤9,
又∵a,b,c均为正数,∴a+b+2c≤3.
证法二:∵a2+b2≥2ab,a2+4c2≥4ac,b2+4c2≥4bc,
∴a2+b2+(2c)2≥ab+2ac+2bc,当且仅当a=b=2c时,取“=”.
又∵a2+b2+4c2=3,∴ab+2ac+2bc≤3,
∴(a+b+2c)2=a2+b2+4c2+2(ab+2ac+2bc)=3+2(ab+2ac+2bc)≤9.
又∵a,b,c均为正数,∴a+b+2c≤3.
(2)∵三个正数的算术平均数不小于它们的调和平均数,∴,当且仅当a=b=2c时,取“=”.
由(1)得a+b+2c≤3,
∴≥3,又∵b=2c,∴≥3.
6.(2022全国乙,23,10分)已知a,b,c都是正数,且=1,证明:
(1)abc≤;
(2).
证明 (1)因为a,b,c都是正数,所以1=,当且仅当a=b=c=时取等号,所以3≤1,即abc≤.
(2)证法一:要证成立,只需证,因为b+c≥2,a+c≥2,a+b≥2,当且仅当a=b=c=时取等号,所以.
证法二:因为b+c≥2,
所以(当且仅当b=c时取等号),
同理(当且仅当a=c时取等号),
(当且仅当a=b时取等号),
所以,
当且仅当a=b=c=时取等号.
7.(2020课标Ⅲ理,23,10分)设a,b,c∈R,a+b+c=0,abc=1.
(1)证明:ab+bc+ca<0;
(2)用max{a,b,c}表示a,b,c的最大值,证明:max{a,b,c}≥.
解析 (1)由题设可知,a,b,c均不为零,所以ab+bc+ca=[(a+b+c)2-(a2+b2+c2)]=-(a2+b2+c2)<0.
(2)不妨设max{a,b,c}=a,因为abc=1,a=-(b+c),
所以a>0,b<0,c<0.由bc≤,可得abc≤,
故a≥,所以max{a,b,c}≥.
21世纪教育网(www.21cnjy.com)
同课章节目录
