22.1.4二次函数的图像与性质导学案(无答案)_北师大版
文档属性
| 名称 | 22.1.4二次函数的图像与性质导学案(无答案)_北师大版 | 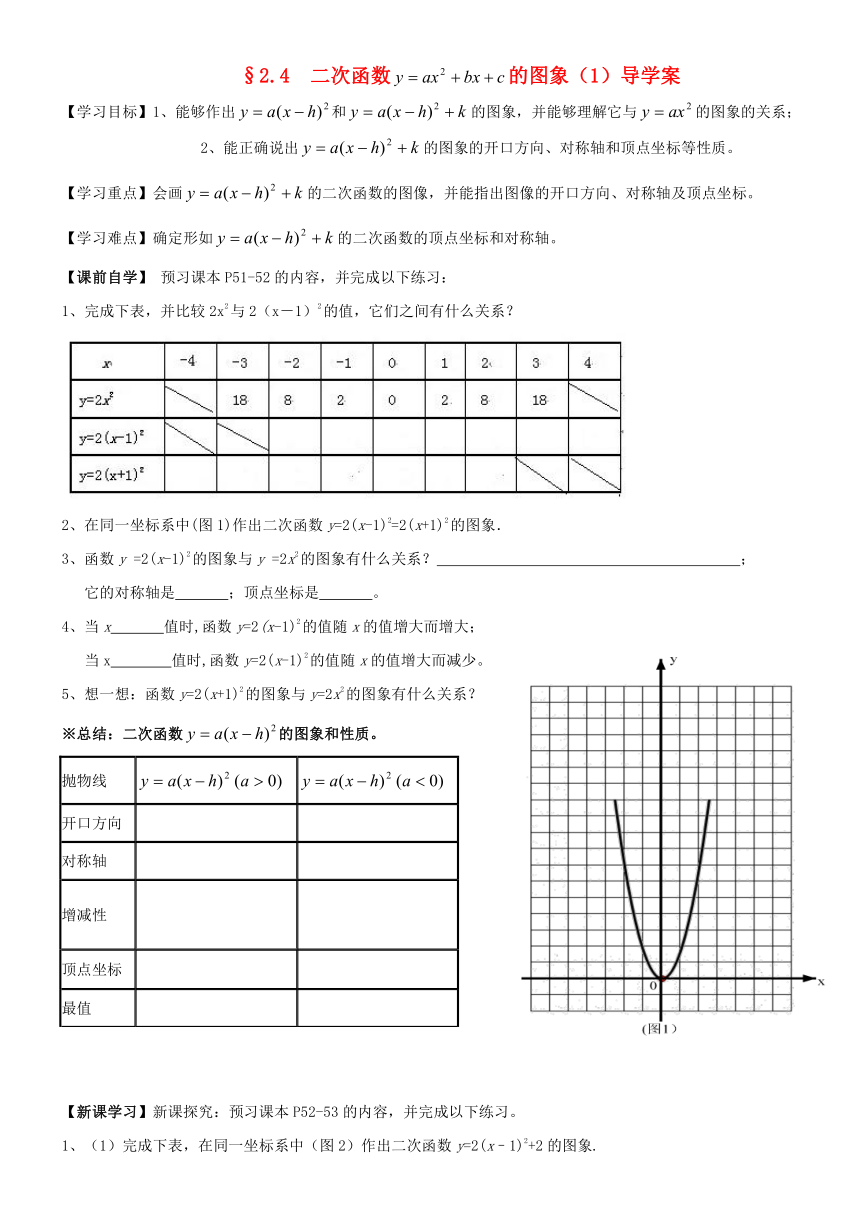 | |
| 格式 | zip | ||
| 文件大小 | 98.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-30 17:02:02 | ||
图片预览

文档简介
§2.4 二次函数的图象(1)导学案
【学习目标】1、能够作出和的图象,并能够理解它与的图象的关系;
2、能正确说出的图象的开口方向、对称轴和顶点坐标等性质。
【学习重点】会画的二次函数的图像,并能指出图像的开口方向、对称轴及顶点坐标。
【学习难点】确定形如的二次函数的顶点坐标和对称轴。
【课前自学】 预习课本P51-52的内容,并完成以下练习:
完成下表,并比较2x2与2(x-1)2的值,它们之间有什么关系?
( http: / / www.21cnjy.com )
2、在同一坐标系中(图1)作出二次函数y=2(x-1)2=2(x+1)2的图象.
3、函数y =2(x-1)2的图象与y ( http: / / www.21cnjy.com )=2x2的图象有什么关系? ;
它的对称轴是 ;顶点坐标是 。
4、当x 值时,函数y=2(x-1)2的值随x的值增大而增大;
当x 值时,函数y=2(x-1)2的值随x的值增大而减少。
5、想一想:函数y=2(x+1)2的图象与y=2x2的图象有什么关系?
※总结:二次函数的图象和性质。
抛物线
开口方向
对称轴
增减性
顶点坐标
最值
【新课学习】新课探究:预习课本P52-53的内容,并完成以下练习。
1、(1)完成下表,在同一坐标系中(图2)作出二次函数y=2(x–1)2+2的图象.
x -2 -1 0 1 2 3 4
(2)二次函数的图象是 ;开口是 ;对称轴是 ;顶点坐标是 。
2、结合图象探究:
的图象可以看成y=2x 的图象,
先沿 轴整体向 平移 个单位;
再沿 轴整体向 平移 个单位得到的。
3、想一想:
(1)二次函数的图象是 ;
开口是 ;对称轴是 ;顶点坐标是 。
(2)的图象与y =2x2的图象有什么关系?
总结:
二次函数的性质。
抛物线
开口方向
对称轴
增减性
顶点坐标
最值
【例题学习】
【例题学习】
(1)二次函数y=–0.5(x+1)2的开口方向是 ;对称轴是 ;顶点坐标是 。
(2)对于二次函数y=2(x–2)2+5,当x 时,y的值随x值的增大而增大;
当x 时,y的值随x值的增大而减小。
【巩固练习】
1、指出下列函数图象的开口方向、对称轴和顶点坐标、增减性和最值:
(1)y=2(x+3)2–2的开口方向是 ;对称轴是 ;顶点坐标是 ;
当x 时,y的值随x值的增大而增大,最小值是 。
(2)y=–0.3(x–1)2+5的开口方向是 ;对称轴是 ;顶点坐标是 ;
当x 时,y的值随x值的增大而增大,最大值是 。
2、将二次函数y=–2x2的图像向上平移2个单位,再向左平移3个单位,得到二次函数是 。
§2.4 二次函数的图象(1)当堂训练
1、抛物线是y=-2x2+1的顶点坐标是( )
A.(-2,1); B.(0,1); C.(1,0); D.(1,-2)。
2、抛物线y=2(x-3)2-5的开口方向是 ;对称轴 ;顶点坐标是 。
3、抛物线y=0.5(x+4)2+2,当x= 时,y有最 值,值为 。
4、对于二次函数y=–(x+1)2-5,当x 时,y的值随x值的增大而增大;
5、将抛物线y=2x2先向右平移3个单位,再向下平移2个单位,所得到的抛物线的
关系式为:__ _____。
【学习目标】1、能够作出和的图象,并能够理解它与的图象的关系;
2、能正确说出的图象的开口方向、对称轴和顶点坐标等性质。
【学习重点】会画的二次函数的图像,并能指出图像的开口方向、对称轴及顶点坐标。
【学习难点】确定形如的二次函数的顶点坐标和对称轴。
【课前自学】 预习课本P51-52的内容,并完成以下练习:
完成下表,并比较2x2与2(x-1)2的值,它们之间有什么关系?
( http: / / www.21cnjy.com )
2、在同一坐标系中(图1)作出二次函数y=2(x-1)2=2(x+1)2的图象.
3、函数y =2(x-1)2的图象与y ( http: / / www.21cnjy.com )=2x2的图象有什么关系? ;
它的对称轴是 ;顶点坐标是 。
4、当x 值时,函数y=2(x-1)2的值随x的值增大而增大;
当x 值时,函数y=2(x-1)2的值随x的值增大而减少。
5、想一想:函数y=2(x+1)2的图象与y=2x2的图象有什么关系?
※总结:二次函数的图象和性质。
抛物线
开口方向
对称轴
增减性
顶点坐标
最值
【新课学习】新课探究:预习课本P52-53的内容,并完成以下练习。
1、(1)完成下表,在同一坐标系中(图2)作出二次函数y=2(x–1)2+2的图象.
x -2 -1 0 1 2 3 4
(2)二次函数的图象是 ;开口是 ;对称轴是 ;顶点坐标是 。
2、结合图象探究:
的图象可以看成y=2x 的图象,
先沿 轴整体向 平移 个单位;
再沿 轴整体向 平移 个单位得到的。
3、想一想:
(1)二次函数的图象是 ;
开口是 ;对称轴是 ;顶点坐标是 。
(2)的图象与y =2x2的图象有什么关系?
总结:
二次函数的性质。
抛物线
开口方向
对称轴
增减性
顶点坐标
最值
【例题学习】
【例题学习】
(1)二次函数y=–0.5(x+1)2的开口方向是 ;对称轴是 ;顶点坐标是 。
(2)对于二次函数y=2(x–2)2+5,当x 时,y的值随x值的增大而增大;
当x 时,y的值随x值的增大而减小。
【巩固练习】
1、指出下列函数图象的开口方向、对称轴和顶点坐标、增减性和最值:
(1)y=2(x+3)2–2的开口方向是 ;对称轴是 ;顶点坐标是 ;
当x 时,y的值随x值的增大而增大,最小值是 。
(2)y=–0.3(x–1)2+5的开口方向是 ;对称轴是 ;顶点坐标是 ;
当x 时,y的值随x值的增大而增大,最大值是 。
2、将二次函数y=–2x2的图像向上平移2个单位,再向左平移3个单位,得到二次函数是 。
§2.4 二次函数的图象(1)当堂训练
1、抛物线是y=-2x2+1的顶点坐标是( )
A.(-2,1); B.(0,1); C.(1,0); D.(1,-2)。
2、抛物线y=2(x-3)2-5的开口方向是 ;对称轴 ;顶点坐标是 。
3、抛物线y=0.5(x+4)2+2,当x= 时,y有最 值,值为 。
4、对于二次函数y=–(x+1)2-5,当x 时,y的值随x值的增大而增大;
5、将抛物线y=2x2先向右平移3个单位,再向下平移2个单位,所得到的抛物线的
关系式为:__ _____。
同课章节目录
