2023年秋数学鲁教版(五四制)九年级上册 3.7 二次函数与一元二次方程 教案
文档属性
| 名称 | 2023年秋数学鲁教版(五四制)九年级上册 3.7 二次函数与一元二次方程 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 83.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 14:32:19 | ||
图片预览

文档简介
3.7 二次函数与一元二次方程
教学目标
1、掌握二次函数图像与x轴的交点情况,会求抛物线与x轴的交点坐标;
2、理解二次函数的图像和x轴的交点与一元二次方程的方程根的关系;
3、会用判别式 判断抛物线与x轴的交点情况。
教学难点
1、熟练判断二次函数的图像和x轴的交点与一元二次方程的方程根的关系;
2、会用判别式 判断抛物线与x轴的交点情况。
教学过程
一、复习引入
下列二次函数的图象与x轴有公共点吗 如果有,公共点的横坐标是多少 当x取公共点的横坐标时,函数的值是多少 由此,你能得出相应的一元二次方程的根吗
y=x+x-2
(2)y=x-6x+9
(3)y=x-x+1
二、探究新知
一次函数y=x+1的图象与x轴的交点为( , )
一元一次方程x+2=0的根为________
思考:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根
探索活动
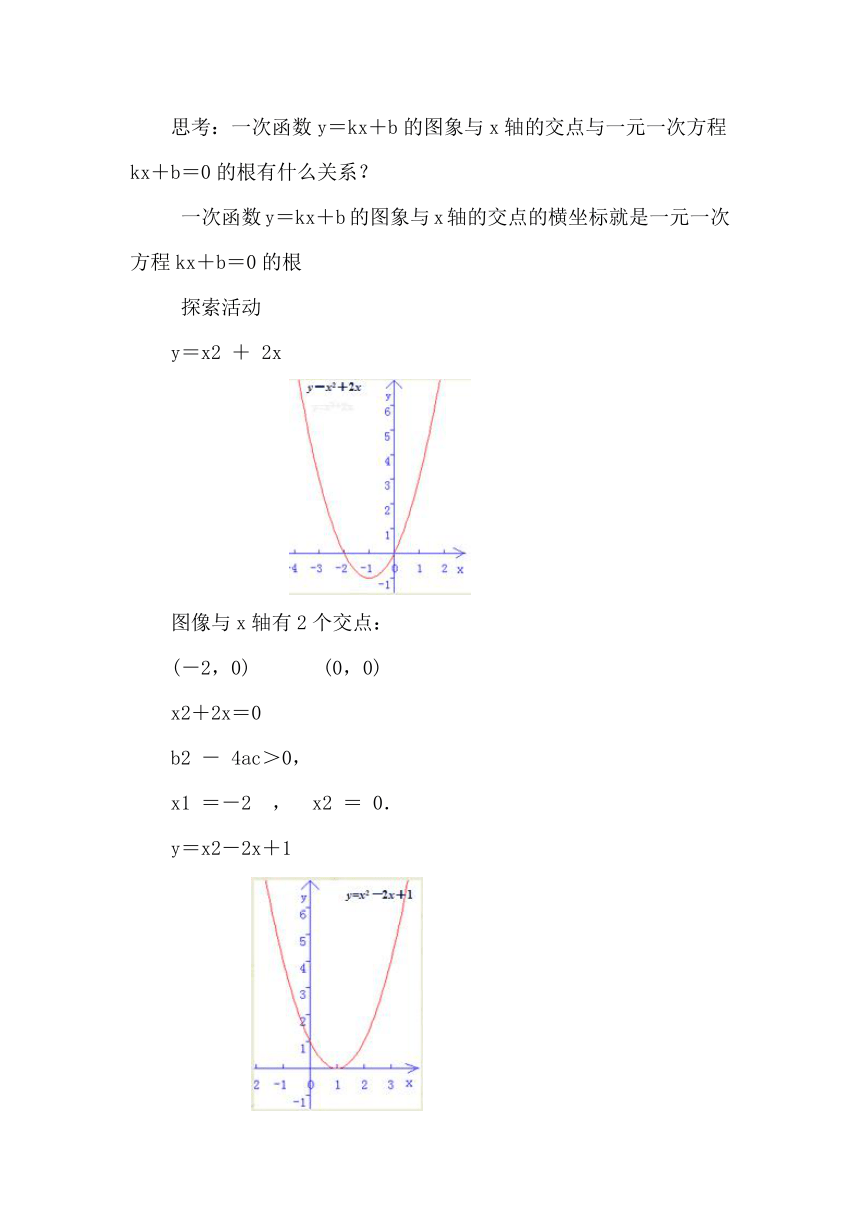
y=x2 + 2x
图像与x轴有2个交点:
(-2,0) (0,0)
x2+2x=0
b2 - 4ac>0,
x1 =-2 , x2 = 0.
y=x2-2x+1
图像与x轴有1个交点:(1,0).
x2-2x+1=0
b2-4ac=0,
x1=x2=1.
y=x2-2x+2
图像与x轴没有交点.
x2-2x+2=0
b2-4ac<0,
没有实数根.
y=x2+2x y=x2-2x+1 y=x2-2x+2
图像与x轴有2个交点. 图像与x轴有1个交点.
图像与x轴没有交点.
x2+2x=0 x2-2x+1=0 x2-2x+2=0
b2-4ac> 0 b2-4ac=0 b2- 4ac< 0
二次函数y=ax2+bx+c的图像和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图像和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
抛物线 y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
1.b2-4ac>0 一元二次方程ax2 + bx+c=0有两个不等的实数根.
抛物线y=ax2 + bx + c与x轴有两个交点.
2. b2-4ac=0 一元二次方程ax2 + bx + c = 0有两个相等的实数根.
抛物线y = ax2 + bx + c与x轴有唯一公共点.
3. b2-4ac<0 一元二次方程ax2 + bx + c=0没有实数根.
抛物线y=ax2 + bx + c与x轴没有公共点.
三、典例精析
例1 阅读材料,解答问题.
利用图象法解一元二次不等式:x2-2x-3>0.
例2
(1)观察图象,直接写出一元二次不等式x2-2x-3<0的解集是____________;
(2)仿照上例,用图象法解一元二次不等式:x2-1>0.
巩固练习
同学们做练习题
课堂小结
谈谈你的收获
教学目标
1、掌握二次函数图像与x轴的交点情况,会求抛物线与x轴的交点坐标;
2、理解二次函数的图像和x轴的交点与一元二次方程的方程根的关系;
3、会用判别式 判断抛物线与x轴的交点情况。
教学难点
1、熟练判断二次函数的图像和x轴的交点与一元二次方程的方程根的关系;
2、会用判别式 判断抛物线与x轴的交点情况。
教学过程
一、复习引入
下列二次函数的图象与x轴有公共点吗 如果有,公共点的横坐标是多少 当x取公共点的横坐标时,函数的值是多少 由此,你能得出相应的一元二次方程的根吗
y=x+x-2
(2)y=x-6x+9
(3)y=x-x+1
二、探究新知
一次函数y=x+1的图象与x轴的交点为( , )
一元一次方程x+2=0的根为________
思考:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根
探索活动
y=x2 + 2x
图像与x轴有2个交点:
(-2,0) (0,0)
x2+2x=0
b2 - 4ac>0,
x1 =-2 , x2 = 0.
y=x2-2x+1
图像与x轴有1个交点:(1,0).
x2-2x+1=0
b2-4ac=0,
x1=x2=1.
y=x2-2x+2
图像与x轴没有交点.
x2-2x+2=0
b2-4ac<0,
没有实数根.
y=x2+2x y=x2-2x+1 y=x2-2x+2
图像与x轴有2个交点. 图像与x轴有1个交点.
图像与x轴没有交点.
x2+2x=0 x2-2x+1=0 x2-2x+2=0
b2-4ac> 0 b2-4ac=0 b2- 4ac< 0
二次函数y=ax2+bx+c的图像和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图像和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
抛物线 y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
1.b2-4ac>0 一元二次方程ax2 + bx+c=0有两个不等的实数根.
抛物线y=ax2 + bx + c与x轴有两个交点.
2. b2-4ac=0 一元二次方程ax2 + bx + c = 0有两个相等的实数根.
抛物线y = ax2 + bx + c与x轴有唯一公共点.
3. b2-4ac<0 一元二次方程ax2 + bx + c=0没有实数根.
抛物线y=ax2 + bx + c与x轴没有公共点.
三、典例精析
例1 阅读材料,解答问题.
利用图象法解一元二次不等式:x2-2x-3>0.
例2
(1)观察图象,直接写出一元二次不等式x2-2x-3<0的解集是____________;
(2)仿照上例,用图象法解一元二次不等式:x2-1>0.
巩固练习
同学们做练习题
课堂小结
谈谈你的收获
