22.2 相似三角形的判定同步练习(3) (含答案)沪科版数学九年级上册
文档属性
| 名称 | 22.2 相似三角形的判定同步练习(3) (含答案)沪科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 16:01:10 | ||
图片预览

文档简介
沪科版九年级数学第22章相似性
第2节相似三角形的判定同步练习(3)
姓名:___________班级:___________
一、单选题
1.下列说法正确的是( )
A.两个直角三角形相似
B.两条边对应成比例,一组对应角相等的两个三角形相似
C.有一个角为40°的两个等腰三角形相似
D.有一个角为100°的两个等腰三角形相似
2.如图,点、分别在的边、上,且与不平行.下列条件中,能判定与相似的是( )
A. B. C. D.
3.如图,点E是矩形ABCD的AB边上任意一点,点F是AD边上一点,∠EFC=90°,图中一定相似的三角形是( )
A.①与② B.③与④ C.②与③ D.①与④
(2)(3)(4)(5)
4.如图,△ABC的高CD和高BE相交于D,则与△DOB相似的三角形个数是( )
A.2个 B.3个 C.4个 D.5个
5.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
6.如图,∥,∥,与交于点G,则图中相似三角形共有 对.
(6)(7)
7.如图,,请你补充一个条件: ,使.
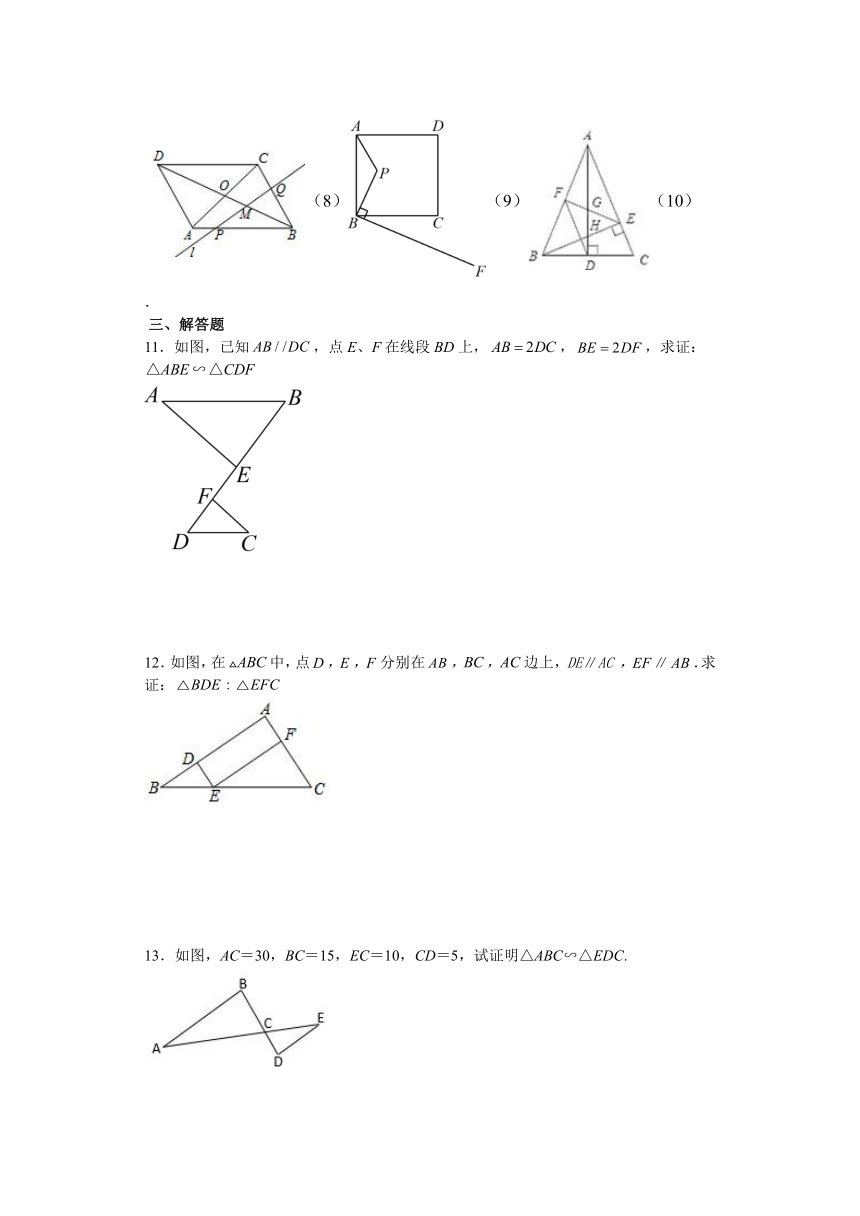
8.如右上图,直线l截□ABCD的边AB、BC和对角线BD于P、Q、M,对角线AC、BD 相交于点O,且PB=3PA,CQ︰BQ=1︰2,则BM︰BO= .
9.如图,已知P是边长为5的正方形内一点,且,于,若在射线上找一点M,使以点B,M,C为顶点的三角形一定与相似,则的值为 .
10.如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC AD=AE2;④S△ABC=4S△ADF.其中正确的有 .
(8)(9)(10)
.
三、解答题
11.如图,已知,点E、F在线段BD上,,,求证:
12.如图,在中,点,,分别在,,边上,,.求证:
13.如图,AC=30,BC=15,EC=10,CD=5,试证明△ABC∽△EDC.
14.如图,四边形的对角线与相交于点,,,,.求证:与是相似三角形.
15.如图,在和中,,.
求证:.
参考答案:
1.D
2.A
3.A
4.B
5.C
6.3
7.(答案不唯一)
8.12:17
9.3或
10.①②③④
11.证明:∵
∴
又∵,
∴
∴.
12.证明:∵,
∴,
∵,
∴,
∴.
13.解:∵,
∴
∴
∴
14.证明:,,,,
,
.
,
与是相似三角形.
15证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
又∵∠ABC=∠ADE,
∴△ABC∽△ADE,
∴.
又∵∠BAD=∠CAE,∴△ABD∽△ACE.
第2节相似三角形的判定同步练习(3)
姓名:___________班级:___________
一、单选题
1.下列说法正确的是( )
A.两个直角三角形相似
B.两条边对应成比例,一组对应角相等的两个三角形相似
C.有一个角为40°的两个等腰三角形相似
D.有一个角为100°的两个等腰三角形相似
2.如图,点、分别在的边、上,且与不平行.下列条件中,能判定与相似的是( )
A. B. C. D.
3.如图,点E是矩形ABCD的AB边上任意一点,点F是AD边上一点,∠EFC=90°,图中一定相似的三角形是( )
A.①与② B.③与④ C.②与③ D.①与④
(2)(3)(4)(5)
4.如图,△ABC的高CD和高BE相交于D,则与△DOB相似的三角形个数是( )
A.2个 B.3个 C.4个 D.5个
5.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
6.如图,∥,∥,与交于点G,则图中相似三角形共有 对.
(6)(7)
7.如图,,请你补充一个条件: ,使.
8.如右上图,直线l截□ABCD的边AB、BC和对角线BD于P、Q、M,对角线AC、BD 相交于点O,且PB=3PA,CQ︰BQ=1︰2,则BM︰BO= .
9.如图,已知P是边长为5的正方形内一点,且,于,若在射线上找一点M,使以点B,M,C为顶点的三角形一定与相似,则的值为 .
10.如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC AD=AE2;④S△ABC=4S△ADF.其中正确的有 .
(8)(9)(10)
.
三、解答题
11.如图,已知,点E、F在线段BD上,,,求证:
12.如图,在中,点,,分别在,,边上,,.求证:
13.如图,AC=30,BC=15,EC=10,CD=5,试证明△ABC∽△EDC.
14.如图,四边形的对角线与相交于点,,,,.求证:与是相似三角形.
15.如图,在和中,,.
求证:.
参考答案:
1.D
2.A
3.A
4.B
5.C
6.3
7.(答案不唯一)
8.12:17
9.3或
10.①②③④
11.证明:∵
∴
又∵,
∴
∴.
12.证明:∵,
∴,
∵,
∴,
∴.
13.解:∵,
∴
∴
∴
14.证明:,,,,
,
.
,
与是相似三角形.
15证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
又∵∠ABC=∠ADE,
∴△ABC∽△ADE,
∴.
又∵∠BAD=∠CAE,∴△ABD∽△ACE.
