山东省青岛市市南区青岛大学附属中学2023-2024学年九年级上学期开学数学试卷(含解析)
文档属性
| 名称 | 山东省青岛市市南区青岛大学附属中学2023-2024学年九年级上学期开学数学试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 00:00:00 | ||
图片预览


文档简介
山东省青岛大学附中2023-2024学年九年级上学期开学数学试卷
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.(3分)下列四个图形中,不是中心对称图形的是( )
A. B.
C. D.
2.(3分)据交通运输部发布消息,某年春节期间,全国共发送旅客29.06亿人次,将29.06亿这个数据用科学记数法可以表示为( )
A.29.06×108 B.2.906×108 C.29.06×109 D.2.906×109
3.(3分)下列运算正确的是( )
A.3a2+5a2=8a4
B.(﹣a3)4÷(﹣a4)3=1
C.(﹣2a2)3﹣(﹣a4)(3a)2=﹣17a6
D.(a﹣b)(a2+ab+b2)=a3﹣b3
4.(3分)不等式组的解集是x>2,则m的取值范围是( )
A.m<1 B.m>1 C.m≤1 D.m≥1
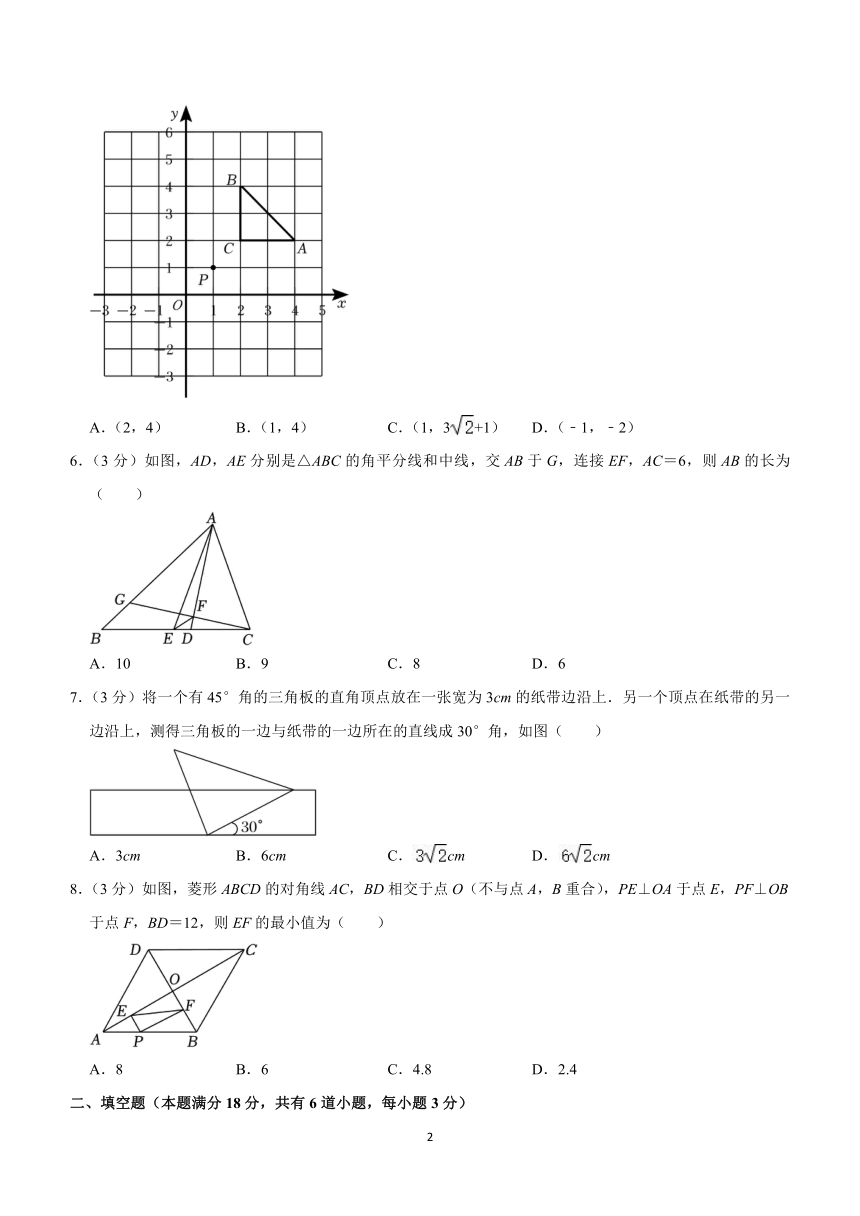
5.(3分)如图,将△ABC向下平移2个单位,再绕点P按逆时针方向旋转90°,点A的对应点A′的坐标是( )
A.(2,4) B.(1,4) C.(1,3+1) D.(﹣1,﹣2)
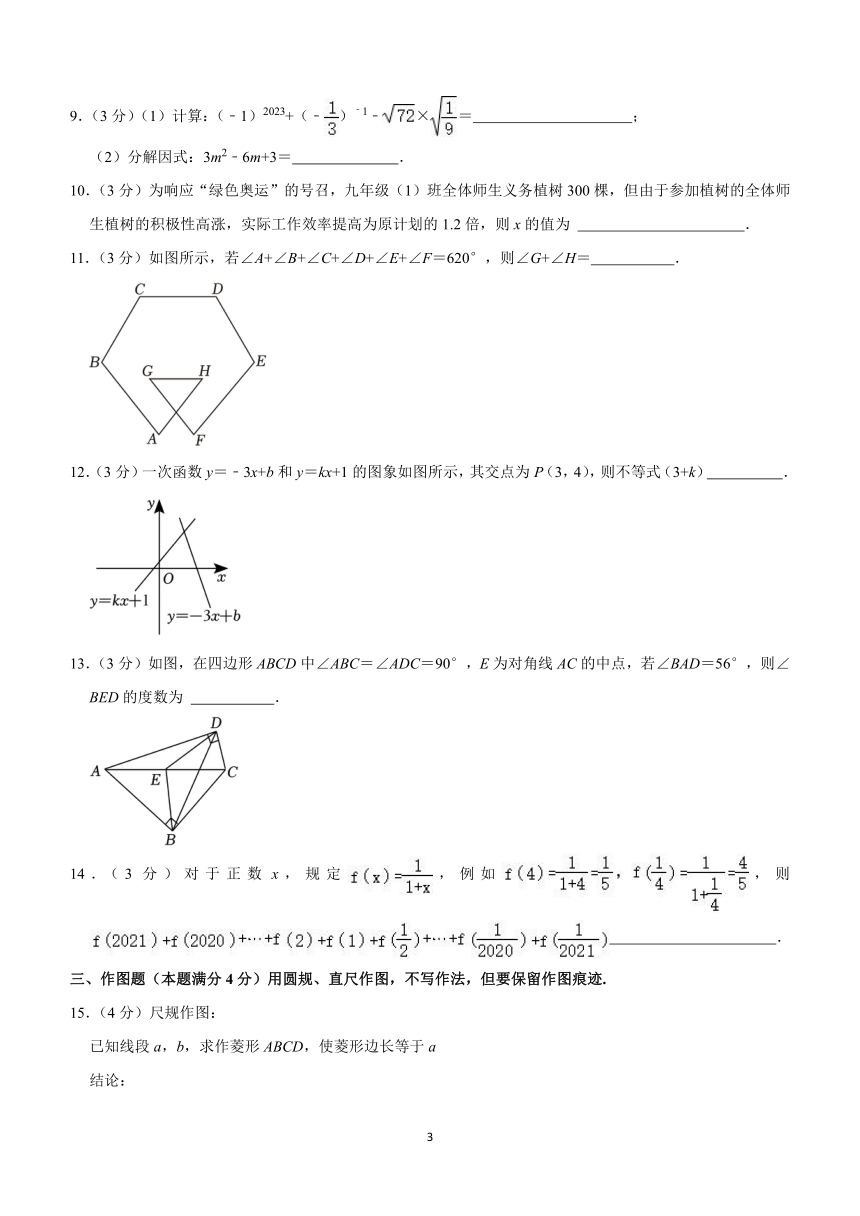
6.(3分)如图,AD,AE分别是△ABC的角平分线和中线,交AB于G,连接EF,AC=6,则AB的长为( )
A.10 B.9 C.8 D.6
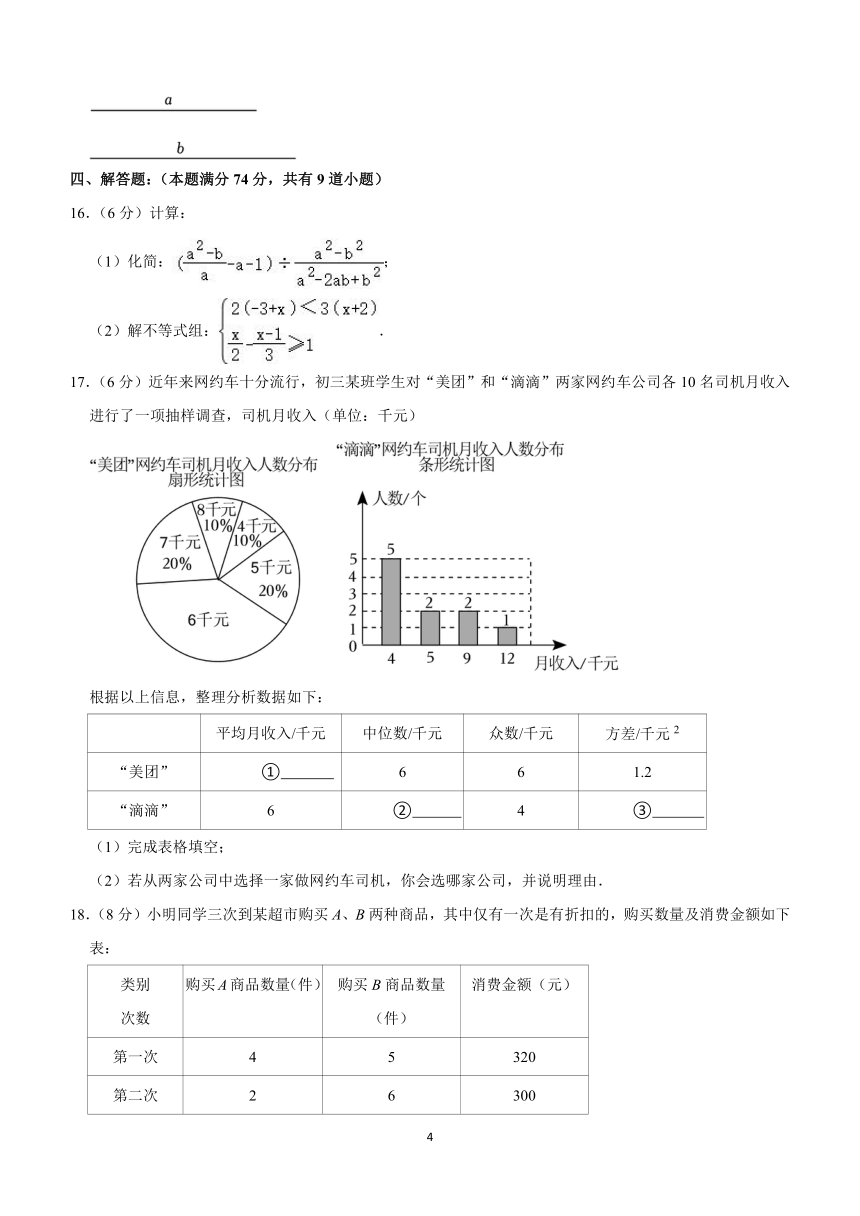
7.(3分)将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图( )
A.3cm B.6cm C.cm D.cm
8.(3分)如图,菱形ABCD的对角线AC,BD相交于点O(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,BD=12,则EF的最小值为( )
A.8 B.6 C.4.8 D.2.4
二、填空题(本题满分18分,共有6道小题,每小题3分)
9.(3分)(1)计算:(﹣1)2023+(﹣)﹣1﹣×= ;
(2)分解因式:3m2﹣6m+3= .
10.(3分)为响应“绿色奥运”的号召,九年级(1)班全体师生义务植树300棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,则x的值为 .
11.(3分)如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=620°,则∠G+∠H= .
12.(3分)一次函数y=﹣3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式(3+k) .
13.(3分)如图,在四边形ABCD中∠ABC=∠ADC=90°,E为对角线AC的中点,若∠BAD=56°,则∠BED的度数为 .
14.(3分)对于正数x,规定,例如,则 .
三、作图题(本题满分4分)用圆规、直尺作图,不写作法,但要保留作图痕迹.
15.(4分)尺规作图:
已知线段a,b,求作菱形ABCD,使菱形边长等于a
结论:
四、解答题:(本题满分74分,共有9道小题)
16.(6分)计算:
(1)化简:;
(2)解不等式组:.
17.(6分)近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)
根据以上信息,整理分析数据如下:
平均月收入/千元 中位数/千元 众数/千元 方差/千元2
“美团” ① 6 6 1.2
“滴滴” 6 ② 4 ③
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
18.(8分)小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别次数 购买A商品数量(件) 购买B商品数量(件) 消费金额(元)
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元
19.(8分)“节能减排,绿色出行”,越来越多的人喜欢骑自行车出行.某自行车车行经营的A型自行车去年销售总额为60000元,那么今年的销售总量需要比去年增加20%.请解答以下问题:
(1)A型自行车今年每辆售价为多少?
(2)该车行今年计划新进一批A型车和新款B型车共80辆,且B型进货数量不超过A型车数量的3倍.A型车和B型车每辆的进价分别为400元和500元,B型车每辆的售价为700元
20.(8分)如图,在平面直角坐标系xOy中,一次函数,与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)请直接写出k、b的值;k= ,b= .
(2)若D线段OC上的动点,过D作DE∥y轴交AC于点E.
①设D点的横坐标为x,线段DE的长为y,则y与x的函数关系式为 ;
②若△AOD为等腰三角形,请求出点D的坐标.
(3)平面内是否存在一点P,使以O、A、C、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标,请说明理由.
21.(8分)如图,平行四边形ABCD的对角线AC、BD交于点O,E为OC中点,连接CH与DH.
(1)求证:△BCE≌△HOE;
(2)当四边形ABCD是怎样的特殊四边形时,四边形OCHD为菱形?请说明理由.
22.(8分)甲、乙两名同学沿直线进行登山,甲、乙沿相同的路线同时从山脚出发到达山顶甲同学到达山顶休息1h后再沿原路下山,他们离山脚的距离S(km)(h)变化的图象如图所示,根据图象中的有关信息回答下列问题:
(1)甲同学上山过程中S甲与t的函数解析式为 ;点D的坐标为 .
(2)若甲同学下山时在点F处与乙同学相遇,此时点F与山顶的距离为0.75km.
①求甲同学下山过程中S与t的函数解析式;
②相遇后甲、乙各自继续下山和上山,求当乙到达山顶时,甲与乙的距离是多少千米.
23.(10分)【问题提出】
如果从1,2,3……m,m个连续的自然数中选择n个连续的自然数(n≤m)
【问题探究】
为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,最后得出一般性的结论
探究一:
如果从1,2,3……m,m个连续的自然数中选择2个连续的自然数
如图1,当m=3,n=2时;
如图2,当m=4,n=2时,2;2,3;3,4这3种不同的选择方法;
如图3,当m=5,n=2时 种不同的选择方法;
……
由上可知:从m个连续的自然数中选择2个连续的自然数,有 种不同的选择方法.
探究二:
如果从1,2,3……100,100个连续的自然数中选择3个(n≤100)个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空
1 2 3 … 93 94 95 96 97 98 99 100
从100个连续的自然数中选择3个连续的自然数,有 种不同的选择方法;
从100个连续的自然数中选择4个连续的自然数,有 种不同的选择方法;
……
从100个连续的自然数中选择8个连续的自然数,有 种不同的选择方法;
……
由上可知:如果从1,2,3……100,100个连续的自然数中选择n(n≤100),有 种不同的选择方法.
【问题解决】
如果从1,2,3……m,m个连续的自然数中选择n个连续的自然数(n≤m) 种不同的选择方法.
【实际应用】
我们运用上面探究得到的结论,可以解决生活中的一些实际问题.
(1)今年国庆七天长假期间,小亮想参加某旅行社组织的青岛两日游,在出行日期上 种不同的选择.
(2)星期天,小明、小强和小华三个好朋友去电影院观看《我和我的祖国》,售票员李阿姨为他们提供了第七排3号到15号的电影票让他们选择,则一共有 种不同的选择方法.
【拓展延伸】
如图4,将一个2×2的图案放置在8×6的方格纸中,使它恰好盖住其中的四个小正方形 种不同的放置方法.
24.(12分)如图,在平面直角坐标系中,O是坐标原点,B分别在x轴与y轴上,已知OA=6,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)求△OPD的面积S关于t的函数解析式;
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在
答案解析
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.(3分)下列四个图形中,不是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形的定义(绕一个点旋转180°能够与自身重合的图形)判断即可.
【解答】解:选项A、C、D中的图形都能找到一个点,所以是中心对称图形.
选项B中的图形不能找到一个点,使图形绕某一点旋转180°后与原来的图形重合.
故选:B.
【点评】本题考查的是中心对称图形,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
2.(3分)据交通运输部发布消息,某年春节期间,全国共发送旅客29.06亿人次,将29.06亿这个数据用科学记数法可以表示为( )
A.29.06×108 B.2.906×108 C.29.06×109 D.2.906×109
【分析】将一个数表示成a×10n的形式,其中1≤|a|<10,n为整数,这种记数方法叫做科学记数法,据此即可得出答案.
【解答】解:29.06亿=2906000000=2.906×109,
故选:D.
【点评】本题考查科学记数法,熟练掌握其定义是解题的关键.
3.(3分)下列运算正确的是( )
A.3a2+5a2=8a4
B.(﹣a3)4÷(﹣a4)3=1
C.(﹣2a2)3﹣(﹣a4)(3a)2=﹣17a6
D.(a﹣b)(a2+ab+b2)=a3﹣b3
【分析】利用整式的混合运算法则计算并判断.
【解答】解:3a2+4a2=8a3,A选项错误;
(﹣a3)4÷(﹣a2)3=﹣1,B选项错误;
(﹣5a2)3﹣(﹣a5)(3a)2
=﹣5a6+9a8
=a6,C选项错误;
(a﹣b)(a2+ab+b4)=a3﹣b3,D选项正确.
故选:D.
【点评】本题考查了整式的混合运算,解题的关键是掌握整式的混合运算法则.
4.(3分)不等式组的解集是x>2,则m的取值范围是( )
A.m<1 B.m>1 C.m≤1 D.m≥1
【分析】根据解不等式,可得每个不等式的解集,再根据每个不等式的解集,可得不等式组的解集,根据不等式的解集,可得答案.
【解答】解:∵不等式组的解集是x>2,
解不等式①得x>8,
解不等式②得x>m+1,
∵不等式组的解集是x>2,
∴m+5≤2,
m≤1,
故选:C.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
5.(3分)如图,将△ABC向下平移2个单位,再绕点P按逆时针方向旋转90°,点A的对应点A′的坐标是( )
A.(2,4) B.(1,4) C.(1,3+1) D.(﹣1,﹣2)
【分析】根据平移和旋转的性质,将△ABC向下平移2个单位,再绕点P按逆时针方向旋转90°,得到△A′B′C′,即可得点A的对应点A′的坐标.
【解答】解:如图,
则△A'B'C'为所求,
∴点A的对应点A′的坐标是(2,4),
故选:A.
【点评】本题考查了坐标与图形变换﹣旋转、平移,解决本题的关键是掌握旋转的性质.
6.(3分)如图,AD,AE分别是△ABC的角平分线和中线,交AB于G,连接EF,AC=6,则AB的长为( )
A.10 B.9 C.8 D.6
【分析】首先证明△ACG是等腰三角形,则AG=AC=6,FG=CF,则EF是△BCG的中位线,利用三角形的中位线定理即可求解.
【解答】解:∵AD为△ABC的角平分线,CG⊥AD,
∴△ACG是等腰三角形,
∴AG=AC,
∵AC=6,
∴AG=AC=6,FG=CF,
∵AE为△ABC的中线,
∴EF是△BCG的中位线,
∴BG=7EF=2,
∴AB=AG+BG=8,
故选:C.
【点评】本题考查了等腰三角形的判定以及三角形的中位线定理,正确证明FG=CF是关键.
7.(3分)将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图( )
A.3cm B.6cm C.cm D.cm
【分析】过另一个顶点C作垂线CD如图,可得直角三角形,根据直角三角形中30°角所对的边等于斜边的一半,可求出有45°角的三角板的直角边,再由等腰直角三角形求出最大边.
【解答】解:过点C作CD⊥AD,∴CD=3cm,
在直角三角形ADC中,
∵∠CAD=30°,
∴AC=2CD=2×3=6cm,
又∵三角板是有45°角的三角板,
∴AB=AC=5cm,
∴BC2=AB2+AC5=62+52=72,
∴BC=6,
故选:D.
【点评】此题考查的知识点是含30°角的直角三角形及等腰直角三角形问题,关键是先求得直角边,再由勾股定理求出最大边.
8.(3分)如图,菱形ABCD的对角线AC,BD相交于点O(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,BD=12,则EF的最小值为( )
A.8 B.6 C.4.8 D.2.4
【分析】连接OP,作OH⊥AB于点H,由菱形的性质得AC⊥BD,OA=OC=AC=8,OB=OD=BD=6,由勾股定理得AB==10,由×10OH=×8×6=S△AOB,求得OH=4.8,再证明四边形PEOF是矩形,则EF=OP,因为OP≥OH,所以EF≥4.8,则EF的最小值为4.8,于是得到问题的答案.
【解答】解:连接OP,作OH⊥AB于点H,
∵四边形ABCD是菱形,对角线AC,
∴AC⊥BD,OA=OC=×16=8BD=,
∴∠AOB=90°,
∴AB===10,
∵AB OH=△AOB,
∴×10OH=,
解得OH=6.8,
∵PE⊥OA于点E,PF⊥OB于点F,
∴∠PEO=∠PFO=∠EOF=90°,
∴四边形PEOF是矩形,
∴EF=OP,
∴OP≥OH,
∴EF≥4.5,
∴EF的最小值为4.8,
故选:C.
【点评】此题重点考查菱形的性质、矩形的判定与性质、勾股定理、根据面积等式求线段的长度、垂线段最短等知识与方法,正确地作出所需要的辅助线是解题的关键.
二、填空题(本题满分18分,共有6道小题,每小题3分)
9.(3分)(1)计算:(﹣1)2023+(﹣)﹣1﹣×= ﹣4﹣2 ;
(2)分解因式:3m2﹣6m+3= 3(m﹣1)2 .
【分析】(1)原式利用乘方的意义,负整数指数幂法则,以及二次根式乘法法则计算即可得到结果;
(2)原式提取公因式,再利用完全平方公式分解即可.
【解答】解:(1)原式=﹣1﹣3﹣
=﹣1﹣7﹣2
=﹣7﹣2;
(2)原式=7(m2﹣2m+4)
=3(m﹣1)6.
故答案为:(1)﹣4﹣2;(2)3(m﹣1)2.
【点评】此题考查了提公因式法与公式法的综合运用,实数的运算,负整数指数幂,熟练掌握运算法则是解本题的关键.
10.(3分)为响应“绿色奥运”的号召,九年级(1)班全体师生义务植树300棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,则x的值为 ﹣= .
【分析】原计划每小时植树x棵,实际工作效率提高为原计划的1.2倍,故每小时植1.2x棵,原计划植300棵树可用时小时,实际用了小时,根据关键语句“结果提前20分钟完成任务”可得方程﹣=.
【解答】解:原计划每小时植树x棵,实际工作效率提高为原计划的1.2倍,由题意得:
﹣=,
故答案为:﹣=.
【点评】此题主要考查了由实际问题抽象出分式方程,关键是弄清题意,表示出原计划植300棵树所用时间与实际所用时间.
11.(3分)如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=620°,则∠G+∠H= 100° .
【分析】根据多边形内角和定理可得∠MAF+∠MFA=100°,从而可得答案.
【解答】解:连接AF,如图:
∵六边形ABCDEF的内角和为(6﹣2)×180°=720°,∠MAB+∠B+∠C+∠D+∠E+∠MFE=620°,
∴∠MAF+∠MFA=720°﹣620°=100°,
∴∠AMF=180°﹣(∠MAF+∠MFA)=80°,
∴∠GMH=∠AMF=80°,
∴∠G+∠H=100°,
故答案为:100°.
【点评】本题考查多边形内角和,解题的关键是求出∠MAF+∠MFA=100°.
12.(3分)一次函数y=﹣3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式(3+k) x≥3 .
【分析】由于不等式(3+k)x≥b﹣1就是不等式kx+1≥﹣3x+b,观察图象,直线y=kx+1落在直线y=﹣3x+b上方的部分对应的x的取值范围即为所求.
【解答】解:∵一次函数y=﹣3x+b和y=kx+1的图象交点为P(8,4),
∴当x≥3时,kx+3≥﹣3x+b,
∴不等式(3+k)x≥b﹣8的解集为x≥3.
故答案为x≥3.
【点评】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
13.(3分)如图,在四边形ABCD中∠ABC=∠ADC=90°,E为对角线AC的中点,若∠BAD=56°,则∠BED的度数为 112° .
【分析】由直角三角形斜边中线的性质得到DE=BE=AE,推出∠DAE=∠ADE,∠BAE=∠ABE,得到∠ADE+∠ABE=∠BAD=56°,由三角形外角的性质得到∠DEC=∠DAE+∠ADE,∠BEC=∠BAE+∠ABE,即可推出∠BED=∠BAD+∠ADE+∠ABE=56°+56°=112°.
【解答】解:∵∠ABC=∠ADC=90°,E是AC的中点,
∴DE=ACAC,
∴DE=BE=AE,
∴∠DAE=∠ADE,∠BAE=∠ABE,
∴∠ADE+∠ABE=∠DAE+∠BAE=∠BAD=56°,
∵∠DEC=∠DAE+∠ADE,∠BEC=∠BAE+∠ABE,
∴∠DEC+∠BEC=∠DAE+∠ADE+∠BAE+∠ABE,
∴∠BED=∠BAD+∠ADE+∠ABE=56°+56°=112°.
故答案为:112°.
【点评】本题考查直角三角形斜边的中线,等腰三角形的性质,三角形外角的性质,关键是由直角三角形斜边中线的性质得到DE=BE=AE,由等腰三角形的性质,三角形外角的性质即可求解.
14.(3分)对于正数x,规定,例如,则 .
【分析】计算出f(2),f(),f(3),f()的值,总结出其规律,再求所求的式子的值即可.
【解答】解:∵f(2)=,f(,f(3)=)=,…,
∴f(2)+f()=,f(3)+f(=8,
∴f(x)+f()=1,
∴
=[f(2021)+f()]+[f(2020)+f()]+f(1)
=1×(2021﹣5)+f(1)
=2020+
=.
故答案为:.
【点评】本题考查数字的变化类、有理数的混合运算,代数式求值,解答本题的关键是明确题意,利用题目中的新规定解答.
三、作图题(本题满分4分)用圆规、直尺作图,不写作法,但要保留作图痕迹.
15.(4分)尺规作图:
已知线段a,b,求作菱形ABCD,使菱形边长等于a
结论:
【分析】①作直线m,在m上截取线段AC=b;
②作线段AC的垂直平分线EF,交线段AC于点O;
③以点A为圆心,线段a的长为半径画弧,交直线EF于点B,D;
④分别连接AB,BC,CD,DA;
则四边形ABCD就是所求作的菱形.
【解答】解:如图,四边形ABCD即为所求.
【点评】本题考查了作图﹣复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的作法、菱形的判定.
四、解答题:(本题满分74分,共有9道小题)
16.(6分)计算:
(1)化简:;
(2)解不等式组:.
【分析】(1)先计算括号,再计算乘除即可;
(2)分别求出两个不等式的解集,寻找公共部分即可.
【解答】解:(1)原式=×
=﹣;
(2),
由①可得﹣5+2x<3x+6,
∴x>﹣12,
由②可得3x﹣2x+2≥6,
∴x≥4,
∴不等式组的解集为:x≥5.
【点评】本题考查分式的混合运算,解一元一次不等式组等知识,解题的关键是掌握分式的混合运算法则,属于中考常考题型.
17.(6分)近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)
根据以上信息,整理分析数据如下:
平均月收入/千元 中位数/千元 众数/千元 方差/千元2
“美团” ① 6 6 6 1.2
“滴滴” 6 ② 4.5 4 ③ 7.6
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
【分析】(1)利用平均数、中位数、众数及方差的定义分别计算后即可确定正确的答案;
(2)根据平均数一样,中位数及众数的大小和方差的大小进行选择即可.
【解答】解:(1)①美团平均月收入:1.4+4.8+0.5+1+2.3=6千元;
②滴滴中位数为4.2千元;
③方差:[5×(4﹣4)2+8×1+2×7+36]=7.6千元7;
故答案为:6,4.5;
(2)选美团,因为平均数一样、众数美团大于滴滴,更稳定.
【点评】本题考查了统计的有关知识,解题的关键是能够了解有关的计算公式,难度不大.
18.(8分)小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别次数 购买A商品数量(件) 购买B商品数量(件) 消费金额(元)
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
解答下列问题:
(1)第 三 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元
【分析】(1)由第三次购买的A、B两种商品均比头两次多,总价反而少,可得出第三次购物有折扣;
(2)设A商品的原价为x元/件,B商品的原价为y元/件,根据总价=单价×数量结合前两次购物的数量及总价,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(3)设折扣数为z,根据总价=单价×数量,即可得出关于z的一元一次方程,解之即可得出结论;
(4)设购买A商品m件,则购买B商品(10﹣m)件,根据总价=单价×数量结合消费金额不超过200元,即可得出关于m的一元一次不等式,解之取其中的最小整数即可得出结论.
【解答】解:(1)观察表格数据,可知:第三次购买的A,总价反而少,
∴第三次购买有折扣.
故答案为:三.
(2)设A商品的原价为x元/件,B商品的原价为y元/件,
根据题意得:,
解得:.
答:A商品的原价为30元/件,B商品的原价为40元/件.
(3)设折扣数为z,
根据题意得:5×30×+2×40×,
解得:z=6.
答:折扣数为6.
(4)设购买A商品m件,则购买B商品(10﹣m)件,
根据题意得:30×m+40×,
解得:m≥,
∵m为整数,
∴m的最小值为3.
答:至少购买A商品7件.
【点评】本题考查了一元一次方程的应用、二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)观察三次购物的数量及总价,找出哪次购物有折扣;(2)找准等量关系,正确列出二元一次方程组;(3)找准等量关系,正确列出一元一次方程;(4)根据各数量间的关系,正确列出一元一次不等式.
19.(8分)“节能减排,绿色出行”,越来越多的人喜欢骑自行车出行.某自行车车行经营的A型自行车去年销售总额为60000元,那么今年的销售总量需要比去年增加20%.请解答以下问题:
(1)A型自行车今年每辆售价为多少?
(2)该车行今年计划新进一批A型车和新款B型车共80辆,且B型进货数量不超过A型车数量的3倍.A型车和B型车每辆的进价分别为400元和500元,B型车每辆的售价为700元
【分析】(1)设A型自行车今年每辆售价为x元,则去年每辆售价为(x+100)元,根据题意列出分式方程,解方程即可求解;
(2)设购进A型车a辆,则购进B型车共(80﹣a)辆,求得a≥20,设利润为y元,根据题意,列出函数关系式,根据一次函数的性质即可求解.
【解答】解:(1)设A型自行车今年每辆售价为x元,则去年每辆售价为(x+100)元,
,
解得:x=500,
经检验,x=500是原方程的解,
答:A型自行车今年每辆售价为500元;
(2)解:设购进A型车a辆,则购进B型车共(80﹣a)辆,
依题意,80﹣a≤3a,
解得:a≥20,
根据题意,A型车和B型车每辆的进价分别为400元和500元;B型车每辆的售价为700元,
设利润为y元,则y=(500﹣400)a+(700﹣500)(80﹣a),
即y=16000﹣100a,
∵﹣100<5,
∴当a=20时取得最大值,最大值为16000﹣100×20=14000(元),
∴购进A型车20辆,购进B型车共60辆,获利最多14000元.
【点评】本题考查了分式方程的意义,一元一次不等式的应用,一次函数的应用,根据题意找到等量关系,列出方程与不等式是解题的关键.
20.(8分)如图,在平面直角坐标系xOy中,一次函数,与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)请直接写出k、b的值;k= ,b= 2 .
(2)若D线段OC上的动点,过D作DE∥y轴交AC于点E.
①设D点的横坐标为x,线段DE的长为y,则y与x的函数关系式为 y=﹣x+2 ;
②若△AOD为等腰三角形,请求出点D的坐标.
(3)平面内是否存在一点P,使以O、A、C、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标,请说明理由.
【分析】(1)把点C的坐标代入即可解答.
(2)①由D(x,x),E(x,x+2),可得y=x+2﹣x=﹣x+2;
②求出A(﹣3,0),根据D为线段OC上的动点,△AOD为等腰三角形,可得x2=9,即可求得D(,);
(3)设P(m,n),分三种情况:①当PO,AC为对角线,则PO,AC的中点重合,②当PA,OC为对角线时,PA,OC的中点重合,③当PC,OA为对角线,则PC,OA的中点重合,分别列出方程组,即可解得答案.
【解答】解:(1)把点C的坐标代入y=中可得b=3,
故答案为:,6;
(2)①直线CD的解析式为y=x,
∵DE∥y轴,D点的横坐标为x,
∴D(x,x),x+2),
∴y=DE=x+2﹣x+5,
故答案为:y=﹣x+8,
②在y=x+7中,
∴A(﹣3,0),
∵D(x,x),0),
∴DO6=x2+(x)2=x8,OA2=9,
∵D为线段OC上的动点,△AOD为等腰三角形,
∴x2=9,
解得:x=或x=﹣,舍去),
∴D(,);
(3)存在一点P,使以O,A,C,理由如下:
设P(m,n),
又O(0,0),2),4),
①当PO,AC为对角线,AC的中点重合,
∴,
解得,
∴P(0,4);
②当PA,OC为对角线时,OC的中点重合,
∴,
解得,
∴P(6,5);
③当PC,OA为对角线,OA的中点重合,
∴,
解得,
∴P(﹣7,﹣4);
综上所述,P的坐标为(0,7)或(﹣6.
【点评】本题考查一次函数的综合应用,涉及待定系数法,等腰三角形,平行四边形等知识,解题的关键是分类讨论思想的应用.
21.(8分)如图,平行四边形ABCD的对角线AC、BD交于点O,E为OC中点,连接CH与DH.
(1)求证:△BCE≌△HOE;
(2)当四边形ABCD是怎样的特殊四边形时,四边形OCHD为菱形?请说明理由.
【分析】(1)由ASA证明△BCE≌△HOE即可;
(2)先证四边形BCHO是平行四边形,得CH=OB,CH∥OB,再证四边形OCHD是平行四边形,然后由菱形的判定即可得出结论.
【解答】(1)证明:∵OH∥BC,
∴∠BCE=∠HOE,
∵E是OC的中点,
∴CE=OE,
在△BCE和△HOE中,
,
∴△BCE≌△HOE(ASA);
(2)解:当四边形ABCD是矩形时,四边形OCHD为菱形
由(1)可知,△BCE≌△HOE,
∴BE=HE,
∵CE=OE,
∴四边形BCHO是平行四边形,
∴CH=OB,CH∥OB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,
∴CH=OD,OC=OD,
∴四边形OCHD是平行四边形,
又∵OC=OD,
∴平行四边形OCHD是菱形.
【点评】本题考查了菱形的判定、矩形的性质、全等三角形的判定与性质、平行四边形的判定与性质等知识,熟练掌握菱形的判定和平行四边形的判定与性质是解题的关键.
22.(8分)甲、乙两名同学沿直线进行登山,甲、乙沿相同的路线同时从山脚出发到达山顶甲同学到达山顶休息1h后再沿原路下山,他们离山脚的距离S(km)(h)变化的图象如图所示,根据图象中的有关信息回答下列问题:
(1)甲同学上山过程中S甲与t的函数解析式为 S甲=t ;点D的坐标为 (9,4) .
(2)若甲同学下山时在点F处与乙同学相遇,此时点F与山顶的距离为0.75km.
①求甲同学下山过程中S与t的函数解析式;
②相遇后甲、乙各自继续下山和上山,求当乙到达山顶时,甲与乙的距离是多少千米.
【分析】(1)由图可知,甲同学登山过程中路程s与时间t成正比例函数,设S甲=kt,用待定系数法可求解,当S甲=4时,可得t=8,即可得D的坐标;
(2)①把y=4﹣0.75代入(1)中乙同学上山过程中S与t的函数解析式,求出点F的横坐标,再利用待定系数法求解即可;
②把y=4代入(1)中乙同学上山过程中S与t的函数解析式,求出乙到山顶所用时间,再代入①的关系式求解即可.
【解答】解:(1)设甲同学登山过程中,路程s(千米)与时间t(时)的函数解析式分别为S甲=kt,
由图象得2=4k,
∴k=,
∴解析式为S甲=t;
当S甲=4时,t=8,
∴甲到达山顶时间是3小时,而甲同学到达山顶休息1小时后再沿原路下山,
∴D(9,2),
故答案为:S甲=t;(7;
(2)①当y=4﹣0.75=时,t=,
解得t=,
∴点F(,),
设甲同学下山过程中S与t的函数解析式为s=kt+b,将D(9,)代入得:
则:,
解答,
答:甲同学下山过程中S与t的函数解析式为S=﹣t+13;
②乙到山顶所用时间为:8÷=12(小时),
当t=12时,S=﹣12+13=2,
当乙到山顶时,甲离乙的距离是:4﹣1=8(千米).
答:甲与乙的距离是3千米.
【点评】本题考查学生利用待定系数法求解一次函数关系式,并利用关系式求值的运算技能和从坐标系中提取信息的能力,是一道综合性较强的代数应用题,有一定的能力要求.
23.(10分)【问题提出】
如果从1,2,3……m,m个连续的自然数中选择n个连续的自然数(n≤m)
【问题探究】
为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,最后得出一般性的结论
探究一:
如果从1,2,3……m,m个连续的自然数中选择2个连续的自然数
如图1,当m=3,n=2时;
如图2,当m=4,n=2时,2;2,3;3,4这3种不同的选择方法;
如图3,当m=5,n=2时 4 种不同的选择方法;
……
由上可知:从m个连续的自然数中选择2个连续的自然数,有 m﹣1 种不同的选择方法.
探究二:
如果从1,2,3……100,100个连续的自然数中选择3个(n≤100)个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空
1 2 3 … 93 94 95 96 97 98 99 100
从100个连续的自然数中选择3个连续的自然数,有 98 种不同的选择方法;
从100个连续的自然数中选择4个连续的自然数,有 97 种不同的选择方法;
……
从100个连续的自然数中选择8个连续的自然数,有 93 种不同的选择方法;
……
由上可知:如果从1,2,3……100,100个连续的自然数中选择n(n≤100),有 (100﹣n+1) 种不同的选择方法.
【问题解决】
如果从1,2,3……m,m个连续的自然数中选择n个连续的自然数(n≤m) (m﹣n+1) 种不同的选择方法.
【实际应用】
我们运用上面探究得到的结论,可以解决生活中的一些实际问题.
(1)今年国庆七天长假期间,小亮想参加某旅行社组织的青岛两日游,在出行日期上 6 种不同的选择.
(2)星期天,小明、小强和小华三个好朋友去电影院观看《我和我的祖国》,售票员李阿姨为他们提供了第七排3号到15号的电影票让他们选择,则一共有 11 种不同的选择方法.
【拓展延伸】
如图4,将一个2×2的图案放置在8×6的方格纸中,使它恰好盖住其中的四个小正方形 35 种不同的放置方法.
【分析】探究一:观察规律可知,选择方法的数量比数的个数少1,由此可得结果;
探究二:选择3个连续的自然数,选择方法的数量比数的个数少2,
选择4个连续的自然数,选择方法的数量比数的个数少3,
以此类推,选择8个连续的自然数,选择方法的数量比数的个数少7,
选择n个连续自然数,选择方法的数量比数的个数少(n﹣1);
【问题解决】:将探究二结论中的100换成m即可;
【实际应用】(1)将m=7,n=2,代入之前的结论即可;
(2)将m=13,n=3,代入之前的结论即可;
【拓展延伸】图案向右移动,每次一格,可得横向的放置方法数,图案向下移动,每次一格,可得纵向的放置方法数,两者相乘即为总数.
【解答】解:探究1:当m=5,n=7时,
根据规律可知:
从m个连续的自然数中选择2个连续的自然数,有(m﹣1)种不同的选择方法;
故答案为:6、m﹣1.
探究2:选择5个连续的自然数,选择方法的数量比数的个数少2,
选择4个连续的自然数,选择方法的数量比数的个数少7,
以此类推,选择8个连续的自然数,
选择n个连续自然数,选择方法的数量比数的个数少(n﹣1);
故从100个连续的自然数中选择7个连续的自然数,有100﹣2=98种不同的选择方法;
从100个连续的自然数中选择4个连续的自然数,有100﹣3=97种不同的选择方法;
……
从100个连续的自然数中选择8个连续的自然数,有100﹣7=93种不同的选择方法;
……
由上可知:如果从2,2,3……100,有(100﹣n+7)种不同的选择方法.
故答案为:98、97、100﹣n+1.
【问题解决】
由规律可知:
从m个连续的自然数中选择n个连续的自然数(n≤m),有(m﹣n+1)种不同的选择方法.
故答案为:(m﹣n+2).
【实际应用】
(1)从连续7天选择连续2天,则m=5,总共有(7﹣2+3)=6种选择;
(2)3号到15号总共13张电影票,选择2连号,n=3;
故答案为:6、11.
【拓展延伸】
图案向右移动,每次一格,可得7种放置方法,
图案向下移动,每次一格,6选2,
故总共7×5=35种放置方法.
故答案为:35.
【点评】本题考查了规律型﹣图形的变化类,先从最简单的问题入手,再逐次递进,最后得出一般性的结论是解决此类问题的关键.
24.(12分)如图,在平面直角坐标系中,O是坐标原点,B分别在x轴与y轴上,已知OA=6,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)求△OPD的面积S关于t的函数解析式;
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在
【分析】(1)设直线DP解析式为y=kx+b,将D与C坐标代入求出k与b的值,即可确定出解析式;
(2)当P在AC段时,三角形ODP底OD与高为固定值,求出此时面积;当P在BC段时,底边OD为固定值,表示出高,即可列出S与t的关系式;
(3)存在,分别以BD,DP,BP为底边三种情况考虑,利用勾股定理及图形与坐标性质求出P坐标即可.
【解答】解:(1)∵OA=6,OB=10,
∴C(6,10).
设此时直线DP解析式为y=kx+b,
把D(4,2),10)分别代入得,
,
解得,
∴此时直线DP的函数解析式为y=x+6;
(2)当点P在线段AC上,0≤t<5时,高为7×7×6=6,
当点P在线段BC上,7≤t<8时,高为6+10﹣8t=16﹣2t×2×(16﹣2t)=﹣6t+16,
∴△OPD的面积S关于t的函数解析式为S=;
(3)存在,理由为:
因为BD>BC,所以满足条件的点AC上.
若△BDP为等腰三角形,分三种情况考虑,
①当BD=BP=OB﹣OD=10﹣2=8时,
在Rt△BCP中,BP=5
根据勾股定理得:CP==2,
∴AP=10﹣2,即P(4);
②当BP=DP时,过点P作PQ⊥OB于Q,
∴BQ=DQ=×(10﹣2)=4,
∴OQ=6+4=6,
∴P(8,6);
③当DB=DP=8时,过点D作DE⊥AC于E,
在Rt△DEP中,DE=7,
根据勾股定理得:PE==2,
∴AP=AE+EP=2+8,
∴P(6,2+2),
综上,满足题意的P坐标为(6,6+2)或(6).
【点评】此题属于一次函数综合题,考查了待定系数法确定一次函数解析式,坐标与图形性质,等腰三角形的性质,勾股定理,利用了分类讨论的思想,熟练掌握待定系数法是解本题的关键.
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.(3分)下列四个图形中,不是中心对称图形的是( )
A. B.
C. D.
2.(3分)据交通运输部发布消息,某年春节期间,全国共发送旅客29.06亿人次,将29.06亿这个数据用科学记数法可以表示为( )
A.29.06×108 B.2.906×108 C.29.06×109 D.2.906×109
3.(3分)下列运算正确的是( )
A.3a2+5a2=8a4
B.(﹣a3)4÷(﹣a4)3=1
C.(﹣2a2)3﹣(﹣a4)(3a)2=﹣17a6
D.(a﹣b)(a2+ab+b2)=a3﹣b3
4.(3分)不等式组的解集是x>2,则m的取值范围是( )
A.m<1 B.m>1 C.m≤1 D.m≥1
5.(3分)如图,将△ABC向下平移2个单位,再绕点P按逆时针方向旋转90°,点A的对应点A′的坐标是( )
A.(2,4) B.(1,4) C.(1,3+1) D.(﹣1,﹣2)
6.(3分)如图,AD,AE分别是△ABC的角平分线和中线,交AB于G,连接EF,AC=6,则AB的长为( )
A.10 B.9 C.8 D.6
7.(3分)将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图( )
A.3cm B.6cm C.cm D.cm
8.(3分)如图,菱形ABCD的对角线AC,BD相交于点O(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,BD=12,则EF的最小值为( )
A.8 B.6 C.4.8 D.2.4
二、填空题(本题满分18分,共有6道小题,每小题3分)
9.(3分)(1)计算:(﹣1)2023+(﹣)﹣1﹣×= ;
(2)分解因式:3m2﹣6m+3= .
10.(3分)为响应“绿色奥运”的号召,九年级(1)班全体师生义务植树300棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,则x的值为 .
11.(3分)如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=620°,则∠G+∠H= .
12.(3分)一次函数y=﹣3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式(3+k) .
13.(3分)如图,在四边形ABCD中∠ABC=∠ADC=90°,E为对角线AC的中点,若∠BAD=56°,则∠BED的度数为 .
14.(3分)对于正数x,规定,例如,则 .
三、作图题(本题满分4分)用圆规、直尺作图,不写作法,但要保留作图痕迹.
15.(4分)尺规作图:
已知线段a,b,求作菱形ABCD,使菱形边长等于a
结论:
四、解答题:(本题满分74分,共有9道小题)
16.(6分)计算:
(1)化简:;
(2)解不等式组:.
17.(6分)近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)
根据以上信息,整理分析数据如下:
平均月收入/千元 中位数/千元 众数/千元 方差/千元2
“美团” ① 6 6 1.2
“滴滴” 6 ② 4 ③
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
18.(8分)小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别次数 购买A商品数量(件) 购买B商品数量(件) 消费金额(元)
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元
19.(8分)“节能减排,绿色出行”,越来越多的人喜欢骑自行车出行.某自行车车行经营的A型自行车去年销售总额为60000元,那么今年的销售总量需要比去年增加20%.请解答以下问题:
(1)A型自行车今年每辆售价为多少?
(2)该车行今年计划新进一批A型车和新款B型车共80辆,且B型进货数量不超过A型车数量的3倍.A型车和B型车每辆的进价分别为400元和500元,B型车每辆的售价为700元
20.(8分)如图,在平面直角坐标系xOy中,一次函数,与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)请直接写出k、b的值;k= ,b= .
(2)若D线段OC上的动点,过D作DE∥y轴交AC于点E.
①设D点的横坐标为x,线段DE的长为y,则y与x的函数关系式为 ;
②若△AOD为等腰三角形,请求出点D的坐标.
(3)平面内是否存在一点P,使以O、A、C、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标,请说明理由.
21.(8分)如图,平行四边形ABCD的对角线AC、BD交于点O,E为OC中点,连接CH与DH.
(1)求证:△BCE≌△HOE;
(2)当四边形ABCD是怎样的特殊四边形时,四边形OCHD为菱形?请说明理由.
22.(8分)甲、乙两名同学沿直线进行登山,甲、乙沿相同的路线同时从山脚出发到达山顶甲同学到达山顶休息1h后再沿原路下山,他们离山脚的距离S(km)(h)变化的图象如图所示,根据图象中的有关信息回答下列问题:
(1)甲同学上山过程中S甲与t的函数解析式为 ;点D的坐标为 .
(2)若甲同学下山时在点F处与乙同学相遇,此时点F与山顶的距离为0.75km.
①求甲同学下山过程中S与t的函数解析式;
②相遇后甲、乙各自继续下山和上山,求当乙到达山顶时,甲与乙的距离是多少千米.
23.(10分)【问题提出】
如果从1,2,3……m,m个连续的自然数中选择n个连续的自然数(n≤m)
【问题探究】
为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,最后得出一般性的结论
探究一:
如果从1,2,3……m,m个连续的自然数中选择2个连续的自然数
如图1,当m=3,n=2时;
如图2,当m=4,n=2时,2;2,3;3,4这3种不同的选择方法;
如图3,当m=5,n=2时 种不同的选择方法;
……
由上可知:从m个连续的自然数中选择2个连续的自然数,有 种不同的选择方法.
探究二:
如果从1,2,3……100,100个连续的自然数中选择3个(n≤100)个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空
1 2 3 … 93 94 95 96 97 98 99 100
从100个连续的自然数中选择3个连续的自然数,有 种不同的选择方法;
从100个连续的自然数中选择4个连续的自然数,有 种不同的选择方法;
……
从100个连续的自然数中选择8个连续的自然数,有 种不同的选择方法;
……
由上可知:如果从1,2,3……100,100个连续的自然数中选择n(n≤100),有 种不同的选择方法.
【问题解决】
如果从1,2,3……m,m个连续的自然数中选择n个连续的自然数(n≤m) 种不同的选择方法.
【实际应用】
我们运用上面探究得到的结论,可以解决生活中的一些实际问题.
(1)今年国庆七天长假期间,小亮想参加某旅行社组织的青岛两日游,在出行日期上 种不同的选择.
(2)星期天,小明、小强和小华三个好朋友去电影院观看《我和我的祖国》,售票员李阿姨为他们提供了第七排3号到15号的电影票让他们选择,则一共有 种不同的选择方法.
【拓展延伸】
如图4,将一个2×2的图案放置在8×6的方格纸中,使它恰好盖住其中的四个小正方形 种不同的放置方法.
24.(12分)如图,在平面直角坐标系中,O是坐标原点,B分别在x轴与y轴上,已知OA=6,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)求△OPD的面积S关于t的函数解析式;
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在
答案解析
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.(3分)下列四个图形中,不是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形的定义(绕一个点旋转180°能够与自身重合的图形)判断即可.
【解答】解:选项A、C、D中的图形都能找到一个点,所以是中心对称图形.
选项B中的图形不能找到一个点,使图形绕某一点旋转180°后与原来的图形重合.
故选:B.
【点评】本题考查的是中心对称图形,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
2.(3分)据交通运输部发布消息,某年春节期间,全国共发送旅客29.06亿人次,将29.06亿这个数据用科学记数法可以表示为( )
A.29.06×108 B.2.906×108 C.29.06×109 D.2.906×109
【分析】将一个数表示成a×10n的形式,其中1≤|a|<10,n为整数,这种记数方法叫做科学记数法,据此即可得出答案.
【解答】解:29.06亿=2906000000=2.906×109,
故选:D.
【点评】本题考查科学记数法,熟练掌握其定义是解题的关键.
3.(3分)下列运算正确的是( )
A.3a2+5a2=8a4
B.(﹣a3)4÷(﹣a4)3=1
C.(﹣2a2)3﹣(﹣a4)(3a)2=﹣17a6
D.(a﹣b)(a2+ab+b2)=a3﹣b3
【分析】利用整式的混合运算法则计算并判断.
【解答】解:3a2+4a2=8a3,A选项错误;
(﹣a3)4÷(﹣a2)3=﹣1,B选项错误;
(﹣5a2)3﹣(﹣a5)(3a)2
=﹣5a6+9a8
=a6,C选项错误;
(a﹣b)(a2+ab+b4)=a3﹣b3,D选项正确.
故选:D.
【点评】本题考查了整式的混合运算,解题的关键是掌握整式的混合运算法则.
4.(3分)不等式组的解集是x>2,则m的取值范围是( )
A.m<1 B.m>1 C.m≤1 D.m≥1
【分析】根据解不等式,可得每个不等式的解集,再根据每个不等式的解集,可得不等式组的解集,根据不等式的解集,可得答案.
【解答】解:∵不等式组的解集是x>2,
解不等式①得x>8,
解不等式②得x>m+1,
∵不等式组的解集是x>2,
∴m+5≤2,
m≤1,
故选:C.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
5.(3分)如图,将△ABC向下平移2个单位,再绕点P按逆时针方向旋转90°,点A的对应点A′的坐标是( )
A.(2,4) B.(1,4) C.(1,3+1) D.(﹣1,﹣2)
【分析】根据平移和旋转的性质,将△ABC向下平移2个单位,再绕点P按逆时针方向旋转90°,得到△A′B′C′,即可得点A的对应点A′的坐标.
【解答】解:如图,
则△A'B'C'为所求,
∴点A的对应点A′的坐标是(2,4),
故选:A.
【点评】本题考查了坐标与图形变换﹣旋转、平移,解决本题的关键是掌握旋转的性质.
6.(3分)如图,AD,AE分别是△ABC的角平分线和中线,交AB于G,连接EF,AC=6,则AB的长为( )
A.10 B.9 C.8 D.6
【分析】首先证明△ACG是等腰三角形,则AG=AC=6,FG=CF,则EF是△BCG的中位线,利用三角形的中位线定理即可求解.
【解答】解:∵AD为△ABC的角平分线,CG⊥AD,
∴△ACG是等腰三角形,
∴AG=AC,
∵AC=6,
∴AG=AC=6,FG=CF,
∵AE为△ABC的中线,
∴EF是△BCG的中位线,
∴BG=7EF=2,
∴AB=AG+BG=8,
故选:C.
【点评】本题考查了等腰三角形的判定以及三角形的中位线定理,正确证明FG=CF是关键.
7.(3分)将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图( )
A.3cm B.6cm C.cm D.cm
【分析】过另一个顶点C作垂线CD如图,可得直角三角形,根据直角三角形中30°角所对的边等于斜边的一半,可求出有45°角的三角板的直角边,再由等腰直角三角形求出最大边.
【解答】解:过点C作CD⊥AD,∴CD=3cm,
在直角三角形ADC中,
∵∠CAD=30°,
∴AC=2CD=2×3=6cm,
又∵三角板是有45°角的三角板,
∴AB=AC=5cm,
∴BC2=AB2+AC5=62+52=72,
∴BC=6,
故选:D.
【点评】此题考查的知识点是含30°角的直角三角形及等腰直角三角形问题,关键是先求得直角边,再由勾股定理求出最大边.
8.(3分)如图,菱形ABCD的对角线AC,BD相交于点O(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,BD=12,则EF的最小值为( )
A.8 B.6 C.4.8 D.2.4
【分析】连接OP,作OH⊥AB于点H,由菱形的性质得AC⊥BD,OA=OC=AC=8,OB=OD=BD=6,由勾股定理得AB==10,由×10OH=×8×6=S△AOB,求得OH=4.8,再证明四边形PEOF是矩形,则EF=OP,因为OP≥OH,所以EF≥4.8,则EF的最小值为4.8,于是得到问题的答案.
【解答】解:连接OP,作OH⊥AB于点H,
∵四边形ABCD是菱形,对角线AC,
∴AC⊥BD,OA=OC=×16=8BD=,
∴∠AOB=90°,
∴AB===10,
∵AB OH=△AOB,
∴×10OH=,
解得OH=6.8,
∵PE⊥OA于点E,PF⊥OB于点F,
∴∠PEO=∠PFO=∠EOF=90°,
∴四边形PEOF是矩形,
∴EF=OP,
∴OP≥OH,
∴EF≥4.5,
∴EF的最小值为4.8,
故选:C.
【点评】此题重点考查菱形的性质、矩形的判定与性质、勾股定理、根据面积等式求线段的长度、垂线段最短等知识与方法,正确地作出所需要的辅助线是解题的关键.
二、填空题(本题满分18分,共有6道小题,每小题3分)
9.(3分)(1)计算:(﹣1)2023+(﹣)﹣1﹣×= ﹣4﹣2 ;
(2)分解因式:3m2﹣6m+3= 3(m﹣1)2 .
【分析】(1)原式利用乘方的意义,负整数指数幂法则,以及二次根式乘法法则计算即可得到结果;
(2)原式提取公因式,再利用完全平方公式分解即可.
【解答】解:(1)原式=﹣1﹣3﹣
=﹣1﹣7﹣2
=﹣7﹣2;
(2)原式=7(m2﹣2m+4)
=3(m﹣1)6.
故答案为:(1)﹣4﹣2;(2)3(m﹣1)2.
【点评】此题考查了提公因式法与公式法的综合运用,实数的运算,负整数指数幂,熟练掌握运算法则是解本题的关键.
10.(3分)为响应“绿色奥运”的号召,九年级(1)班全体师生义务植树300棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,则x的值为 ﹣= .
【分析】原计划每小时植树x棵,实际工作效率提高为原计划的1.2倍,故每小时植1.2x棵,原计划植300棵树可用时小时,实际用了小时,根据关键语句“结果提前20分钟完成任务”可得方程﹣=.
【解答】解:原计划每小时植树x棵,实际工作效率提高为原计划的1.2倍,由题意得:
﹣=,
故答案为:﹣=.
【点评】此题主要考查了由实际问题抽象出分式方程,关键是弄清题意,表示出原计划植300棵树所用时间与实际所用时间.
11.(3分)如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=620°,则∠G+∠H= 100° .
【分析】根据多边形内角和定理可得∠MAF+∠MFA=100°,从而可得答案.
【解答】解:连接AF,如图:
∵六边形ABCDEF的内角和为(6﹣2)×180°=720°,∠MAB+∠B+∠C+∠D+∠E+∠MFE=620°,
∴∠MAF+∠MFA=720°﹣620°=100°,
∴∠AMF=180°﹣(∠MAF+∠MFA)=80°,
∴∠GMH=∠AMF=80°,
∴∠G+∠H=100°,
故答案为:100°.
【点评】本题考查多边形内角和,解题的关键是求出∠MAF+∠MFA=100°.
12.(3分)一次函数y=﹣3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式(3+k) x≥3 .
【分析】由于不等式(3+k)x≥b﹣1就是不等式kx+1≥﹣3x+b,观察图象,直线y=kx+1落在直线y=﹣3x+b上方的部分对应的x的取值范围即为所求.
【解答】解:∵一次函数y=﹣3x+b和y=kx+1的图象交点为P(8,4),
∴当x≥3时,kx+3≥﹣3x+b,
∴不等式(3+k)x≥b﹣8的解集为x≥3.
故答案为x≥3.
【点评】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
13.(3分)如图,在四边形ABCD中∠ABC=∠ADC=90°,E为对角线AC的中点,若∠BAD=56°,则∠BED的度数为 112° .
【分析】由直角三角形斜边中线的性质得到DE=BE=AE,推出∠DAE=∠ADE,∠BAE=∠ABE,得到∠ADE+∠ABE=∠BAD=56°,由三角形外角的性质得到∠DEC=∠DAE+∠ADE,∠BEC=∠BAE+∠ABE,即可推出∠BED=∠BAD+∠ADE+∠ABE=56°+56°=112°.
【解答】解:∵∠ABC=∠ADC=90°,E是AC的中点,
∴DE=ACAC,
∴DE=BE=AE,
∴∠DAE=∠ADE,∠BAE=∠ABE,
∴∠ADE+∠ABE=∠DAE+∠BAE=∠BAD=56°,
∵∠DEC=∠DAE+∠ADE,∠BEC=∠BAE+∠ABE,
∴∠DEC+∠BEC=∠DAE+∠ADE+∠BAE+∠ABE,
∴∠BED=∠BAD+∠ADE+∠ABE=56°+56°=112°.
故答案为:112°.
【点评】本题考查直角三角形斜边的中线,等腰三角形的性质,三角形外角的性质,关键是由直角三角形斜边中线的性质得到DE=BE=AE,由等腰三角形的性质,三角形外角的性质即可求解.
14.(3分)对于正数x,规定,例如,则 .
【分析】计算出f(2),f(),f(3),f()的值,总结出其规律,再求所求的式子的值即可.
【解答】解:∵f(2)=,f(,f(3)=)=,…,
∴f(2)+f()=,f(3)+f(=8,
∴f(x)+f()=1,
∴
=[f(2021)+f()]+[f(2020)+f()]+f(1)
=1×(2021﹣5)+f(1)
=2020+
=.
故答案为:.
【点评】本题考查数字的变化类、有理数的混合运算,代数式求值,解答本题的关键是明确题意,利用题目中的新规定解答.
三、作图题(本题满分4分)用圆规、直尺作图,不写作法,但要保留作图痕迹.
15.(4分)尺规作图:
已知线段a,b,求作菱形ABCD,使菱形边长等于a
结论:
【分析】①作直线m,在m上截取线段AC=b;
②作线段AC的垂直平分线EF,交线段AC于点O;
③以点A为圆心,线段a的长为半径画弧,交直线EF于点B,D;
④分别连接AB,BC,CD,DA;
则四边形ABCD就是所求作的菱形.
【解答】解:如图,四边形ABCD即为所求.
【点评】本题考查了作图﹣复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的作法、菱形的判定.
四、解答题:(本题满分74分,共有9道小题)
16.(6分)计算:
(1)化简:;
(2)解不等式组:.
【分析】(1)先计算括号,再计算乘除即可;
(2)分别求出两个不等式的解集,寻找公共部分即可.
【解答】解:(1)原式=×
=﹣;
(2),
由①可得﹣5+2x<3x+6,
∴x>﹣12,
由②可得3x﹣2x+2≥6,
∴x≥4,
∴不等式组的解集为:x≥5.
【点评】本题考查分式的混合运算,解一元一次不等式组等知识,解题的关键是掌握分式的混合运算法则,属于中考常考题型.
17.(6分)近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)
根据以上信息,整理分析数据如下:
平均月收入/千元 中位数/千元 众数/千元 方差/千元2
“美团” ① 6 6 6 1.2
“滴滴” 6 ② 4.5 4 ③ 7.6
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
【分析】(1)利用平均数、中位数、众数及方差的定义分别计算后即可确定正确的答案;
(2)根据平均数一样,中位数及众数的大小和方差的大小进行选择即可.
【解答】解:(1)①美团平均月收入:1.4+4.8+0.5+1+2.3=6千元;
②滴滴中位数为4.2千元;
③方差:[5×(4﹣4)2+8×1+2×7+36]=7.6千元7;
故答案为:6,4.5;
(2)选美团,因为平均数一样、众数美团大于滴滴,更稳定.
【点评】本题考查了统计的有关知识,解题的关键是能够了解有关的计算公式,难度不大.
18.(8分)小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别次数 购买A商品数量(件) 购买B商品数量(件) 消费金额(元)
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
解答下列问题:
(1)第 三 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元
【分析】(1)由第三次购买的A、B两种商品均比头两次多,总价反而少,可得出第三次购物有折扣;
(2)设A商品的原价为x元/件,B商品的原价为y元/件,根据总价=单价×数量结合前两次购物的数量及总价,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(3)设折扣数为z,根据总价=单价×数量,即可得出关于z的一元一次方程,解之即可得出结论;
(4)设购买A商品m件,则购买B商品(10﹣m)件,根据总价=单价×数量结合消费金额不超过200元,即可得出关于m的一元一次不等式,解之取其中的最小整数即可得出结论.
【解答】解:(1)观察表格数据,可知:第三次购买的A,总价反而少,
∴第三次购买有折扣.
故答案为:三.
(2)设A商品的原价为x元/件,B商品的原价为y元/件,
根据题意得:,
解得:.
答:A商品的原价为30元/件,B商品的原价为40元/件.
(3)设折扣数为z,
根据题意得:5×30×+2×40×,
解得:z=6.
答:折扣数为6.
(4)设购买A商品m件,则购买B商品(10﹣m)件,
根据题意得:30×m+40×,
解得:m≥,
∵m为整数,
∴m的最小值为3.
答:至少购买A商品7件.
【点评】本题考查了一元一次方程的应用、二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)观察三次购物的数量及总价,找出哪次购物有折扣;(2)找准等量关系,正确列出二元一次方程组;(3)找准等量关系,正确列出一元一次方程;(4)根据各数量间的关系,正确列出一元一次不等式.
19.(8分)“节能减排,绿色出行”,越来越多的人喜欢骑自行车出行.某自行车车行经营的A型自行车去年销售总额为60000元,那么今年的销售总量需要比去年增加20%.请解答以下问题:
(1)A型自行车今年每辆售价为多少?
(2)该车行今年计划新进一批A型车和新款B型车共80辆,且B型进货数量不超过A型车数量的3倍.A型车和B型车每辆的进价分别为400元和500元,B型车每辆的售价为700元
【分析】(1)设A型自行车今年每辆售价为x元,则去年每辆售价为(x+100)元,根据题意列出分式方程,解方程即可求解;
(2)设购进A型车a辆,则购进B型车共(80﹣a)辆,求得a≥20,设利润为y元,根据题意,列出函数关系式,根据一次函数的性质即可求解.
【解答】解:(1)设A型自行车今年每辆售价为x元,则去年每辆售价为(x+100)元,
,
解得:x=500,
经检验,x=500是原方程的解,
答:A型自行车今年每辆售价为500元;
(2)解:设购进A型车a辆,则购进B型车共(80﹣a)辆,
依题意,80﹣a≤3a,
解得:a≥20,
根据题意,A型车和B型车每辆的进价分别为400元和500元;B型车每辆的售价为700元,
设利润为y元,则y=(500﹣400)a+(700﹣500)(80﹣a),
即y=16000﹣100a,
∵﹣100<5,
∴当a=20时取得最大值,最大值为16000﹣100×20=14000(元),
∴购进A型车20辆,购进B型车共60辆,获利最多14000元.
【点评】本题考查了分式方程的意义,一元一次不等式的应用,一次函数的应用,根据题意找到等量关系,列出方程与不等式是解题的关键.
20.(8分)如图,在平面直角坐标系xOy中,一次函数,与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)请直接写出k、b的值;k= ,b= 2 .
(2)若D线段OC上的动点,过D作DE∥y轴交AC于点E.
①设D点的横坐标为x,线段DE的长为y,则y与x的函数关系式为 y=﹣x+2 ;
②若△AOD为等腰三角形,请求出点D的坐标.
(3)平面内是否存在一点P,使以O、A、C、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标,请说明理由.
【分析】(1)把点C的坐标代入即可解答.
(2)①由D(x,x),E(x,x+2),可得y=x+2﹣x=﹣x+2;
②求出A(﹣3,0),根据D为线段OC上的动点,△AOD为等腰三角形,可得x2=9,即可求得D(,);
(3)设P(m,n),分三种情况:①当PO,AC为对角线,则PO,AC的中点重合,②当PA,OC为对角线时,PA,OC的中点重合,③当PC,OA为对角线,则PC,OA的中点重合,分别列出方程组,即可解得答案.
【解答】解:(1)把点C的坐标代入y=中可得b=3,
故答案为:,6;
(2)①直线CD的解析式为y=x,
∵DE∥y轴,D点的横坐标为x,
∴D(x,x),x+2),
∴y=DE=x+2﹣x+5,
故答案为:y=﹣x+8,
②在y=x+7中,
∴A(﹣3,0),
∵D(x,x),0),
∴DO6=x2+(x)2=x8,OA2=9,
∵D为线段OC上的动点,△AOD为等腰三角形,
∴x2=9,
解得:x=或x=﹣,舍去),
∴D(,);
(3)存在一点P,使以O,A,C,理由如下:
设P(m,n),
又O(0,0),2),4),
①当PO,AC为对角线,AC的中点重合,
∴,
解得,
∴P(0,4);
②当PA,OC为对角线时,OC的中点重合,
∴,
解得,
∴P(6,5);
③当PC,OA为对角线,OA的中点重合,
∴,
解得,
∴P(﹣7,﹣4);
综上所述,P的坐标为(0,7)或(﹣6.
【点评】本题考查一次函数的综合应用,涉及待定系数法,等腰三角形,平行四边形等知识,解题的关键是分类讨论思想的应用.
21.(8分)如图,平行四边形ABCD的对角线AC、BD交于点O,E为OC中点,连接CH与DH.
(1)求证:△BCE≌△HOE;
(2)当四边形ABCD是怎样的特殊四边形时,四边形OCHD为菱形?请说明理由.
【分析】(1)由ASA证明△BCE≌△HOE即可;
(2)先证四边形BCHO是平行四边形,得CH=OB,CH∥OB,再证四边形OCHD是平行四边形,然后由菱形的判定即可得出结论.
【解答】(1)证明:∵OH∥BC,
∴∠BCE=∠HOE,
∵E是OC的中点,
∴CE=OE,
在△BCE和△HOE中,
,
∴△BCE≌△HOE(ASA);
(2)解:当四边形ABCD是矩形时,四边形OCHD为菱形
由(1)可知,△BCE≌△HOE,
∴BE=HE,
∵CE=OE,
∴四边形BCHO是平行四边形,
∴CH=OB,CH∥OB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,
∴CH=OD,OC=OD,
∴四边形OCHD是平行四边形,
又∵OC=OD,
∴平行四边形OCHD是菱形.
【点评】本题考查了菱形的判定、矩形的性质、全等三角形的判定与性质、平行四边形的判定与性质等知识,熟练掌握菱形的判定和平行四边形的判定与性质是解题的关键.
22.(8分)甲、乙两名同学沿直线进行登山,甲、乙沿相同的路线同时从山脚出发到达山顶甲同学到达山顶休息1h后再沿原路下山,他们离山脚的距离S(km)(h)变化的图象如图所示,根据图象中的有关信息回答下列问题:
(1)甲同学上山过程中S甲与t的函数解析式为 S甲=t ;点D的坐标为 (9,4) .
(2)若甲同学下山时在点F处与乙同学相遇,此时点F与山顶的距离为0.75km.
①求甲同学下山过程中S与t的函数解析式;
②相遇后甲、乙各自继续下山和上山,求当乙到达山顶时,甲与乙的距离是多少千米.
【分析】(1)由图可知,甲同学登山过程中路程s与时间t成正比例函数,设S甲=kt,用待定系数法可求解,当S甲=4时,可得t=8,即可得D的坐标;
(2)①把y=4﹣0.75代入(1)中乙同学上山过程中S与t的函数解析式,求出点F的横坐标,再利用待定系数法求解即可;
②把y=4代入(1)中乙同学上山过程中S与t的函数解析式,求出乙到山顶所用时间,再代入①的关系式求解即可.
【解答】解:(1)设甲同学登山过程中,路程s(千米)与时间t(时)的函数解析式分别为S甲=kt,
由图象得2=4k,
∴k=,
∴解析式为S甲=t;
当S甲=4时,t=8,
∴甲到达山顶时间是3小时,而甲同学到达山顶休息1小时后再沿原路下山,
∴D(9,2),
故答案为:S甲=t;(7;
(2)①当y=4﹣0.75=时,t=,
解得t=,
∴点F(,),
设甲同学下山过程中S与t的函数解析式为s=kt+b,将D(9,)代入得:
则:,
解答,
答:甲同学下山过程中S与t的函数解析式为S=﹣t+13;
②乙到山顶所用时间为:8÷=12(小时),
当t=12时,S=﹣12+13=2,
当乙到山顶时,甲离乙的距离是:4﹣1=8(千米).
答:甲与乙的距离是3千米.
【点评】本题考查学生利用待定系数法求解一次函数关系式,并利用关系式求值的运算技能和从坐标系中提取信息的能力,是一道综合性较强的代数应用题,有一定的能力要求.
23.(10分)【问题提出】
如果从1,2,3……m,m个连续的自然数中选择n个连续的自然数(n≤m)
【问题探究】
为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,最后得出一般性的结论
探究一:
如果从1,2,3……m,m个连续的自然数中选择2个连续的自然数
如图1,当m=3,n=2时;
如图2,当m=4,n=2时,2;2,3;3,4这3种不同的选择方法;
如图3,当m=5,n=2时 4 种不同的选择方法;
……
由上可知:从m个连续的自然数中选择2个连续的自然数,有 m﹣1 种不同的选择方法.
探究二:
如果从1,2,3……100,100个连续的自然数中选择3个(n≤100)个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空
1 2 3 … 93 94 95 96 97 98 99 100
从100个连续的自然数中选择3个连续的自然数,有 98 种不同的选择方法;
从100个连续的自然数中选择4个连续的自然数,有 97 种不同的选择方法;
……
从100个连续的自然数中选择8个连续的自然数,有 93 种不同的选择方法;
……
由上可知:如果从1,2,3……100,100个连续的自然数中选择n(n≤100),有 (100﹣n+1) 种不同的选择方法.
【问题解决】
如果从1,2,3……m,m个连续的自然数中选择n个连续的自然数(n≤m) (m﹣n+1) 种不同的选择方法.
【实际应用】
我们运用上面探究得到的结论,可以解决生活中的一些实际问题.
(1)今年国庆七天长假期间,小亮想参加某旅行社组织的青岛两日游,在出行日期上 6 种不同的选择.
(2)星期天,小明、小强和小华三个好朋友去电影院观看《我和我的祖国》,售票员李阿姨为他们提供了第七排3号到15号的电影票让他们选择,则一共有 11 种不同的选择方法.
【拓展延伸】
如图4,将一个2×2的图案放置在8×6的方格纸中,使它恰好盖住其中的四个小正方形 35 种不同的放置方法.
【分析】探究一:观察规律可知,选择方法的数量比数的个数少1,由此可得结果;
探究二:选择3个连续的自然数,选择方法的数量比数的个数少2,
选择4个连续的自然数,选择方法的数量比数的个数少3,
以此类推,选择8个连续的自然数,选择方法的数量比数的个数少7,
选择n个连续自然数,选择方法的数量比数的个数少(n﹣1);
【问题解决】:将探究二结论中的100换成m即可;
【实际应用】(1)将m=7,n=2,代入之前的结论即可;
(2)将m=13,n=3,代入之前的结论即可;
【拓展延伸】图案向右移动,每次一格,可得横向的放置方法数,图案向下移动,每次一格,可得纵向的放置方法数,两者相乘即为总数.
【解答】解:探究1:当m=5,n=7时,
根据规律可知:
从m个连续的自然数中选择2个连续的自然数,有(m﹣1)种不同的选择方法;
故答案为:6、m﹣1.
探究2:选择5个连续的自然数,选择方法的数量比数的个数少2,
选择4个连续的自然数,选择方法的数量比数的个数少7,
以此类推,选择8个连续的自然数,
选择n个连续自然数,选择方法的数量比数的个数少(n﹣1);
故从100个连续的自然数中选择7个连续的自然数,有100﹣2=98种不同的选择方法;
从100个连续的自然数中选择4个连续的自然数,有100﹣3=97种不同的选择方法;
……
从100个连续的自然数中选择8个连续的自然数,有100﹣7=93种不同的选择方法;
……
由上可知:如果从2,2,3……100,有(100﹣n+7)种不同的选择方法.
故答案为:98、97、100﹣n+1.
【问题解决】
由规律可知:
从m个连续的自然数中选择n个连续的自然数(n≤m),有(m﹣n+1)种不同的选择方法.
故答案为:(m﹣n+2).
【实际应用】
(1)从连续7天选择连续2天,则m=5,总共有(7﹣2+3)=6种选择;
(2)3号到15号总共13张电影票,选择2连号,n=3;
故答案为:6、11.
【拓展延伸】
图案向右移动,每次一格,可得7种放置方法,
图案向下移动,每次一格,6选2,
故总共7×5=35种放置方法.
故答案为:35.
【点评】本题考查了规律型﹣图形的变化类,先从最简单的问题入手,再逐次递进,最后得出一般性的结论是解决此类问题的关键.
24.(12分)如图,在平面直角坐标系中,O是坐标原点,B分别在x轴与y轴上,已知OA=6,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)求△OPD的面积S关于t的函数解析式;
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在
【分析】(1)设直线DP解析式为y=kx+b,将D与C坐标代入求出k与b的值,即可确定出解析式;
(2)当P在AC段时,三角形ODP底OD与高为固定值,求出此时面积;当P在BC段时,底边OD为固定值,表示出高,即可列出S与t的关系式;
(3)存在,分别以BD,DP,BP为底边三种情况考虑,利用勾股定理及图形与坐标性质求出P坐标即可.
【解答】解:(1)∵OA=6,OB=10,
∴C(6,10).
设此时直线DP解析式为y=kx+b,
把D(4,2),10)分别代入得,
,
解得,
∴此时直线DP的函数解析式为y=x+6;
(2)当点P在线段AC上,0≤t<5时,高为7×7×6=6,
当点P在线段BC上,7≤t<8时,高为6+10﹣8t=16﹣2t×2×(16﹣2t)=﹣6t+16,
∴△OPD的面积S关于t的函数解析式为S=;
(3)存在,理由为:
因为BD>BC,所以满足条件的点AC上.
若△BDP为等腰三角形,分三种情况考虑,
①当BD=BP=OB﹣OD=10﹣2=8时,
在Rt△BCP中,BP=5
根据勾股定理得:CP==2,
∴AP=10﹣2,即P(4);
②当BP=DP时,过点P作PQ⊥OB于Q,
∴BQ=DQ=×(10﹣2)=4,
∴OQ=6+4=6,
∴P(8,6);
③当DB=DP=8时,过点D作DE⊥AC于E,
在Rt△DEP中,DE=7,
根据勾股定理得:PE==2,
∴AP=AE+EP=2+8,
∴P(6,2+2),
综上,满足题意的P坐标为(6,6+2)或(6).
【点评】此题属于一次函数综合题,考查了待定系数法确定一次函数解析式,坐标与图形性质,等腰三角形的性质,勾股定理,利用了分类讨论的思想,熟练掌握待定系数法是解本题的关键.
同课章节目录
