青岛版数学八年级上册 5.6.5 直角三角形全等的证明课件(共17张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 5.6.5 直角三角形全等的证明课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 443.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 15:31:07 | ||
图片预览





文档简介
(共17张PPT)
第5章 几何证明初步
5.6 几何证明举例
第5课时 直角三角形全等的证明
学习目标
进一步熟悉证明题的题型,根据三角形全等推导“HL”定理;
熟练应用“斜边、直角边”定理及其它三角形全等的判定方法进行证明;
增强合作意识,提高逻辑思维能力.
复习导入
要判定两个三角形全等,你有哪些方法?
边角边 简称 “SAS”
角边角 简称 “ASA”
边边边 简称 “SSS”
角角边 简称 “AAS”
探究新知
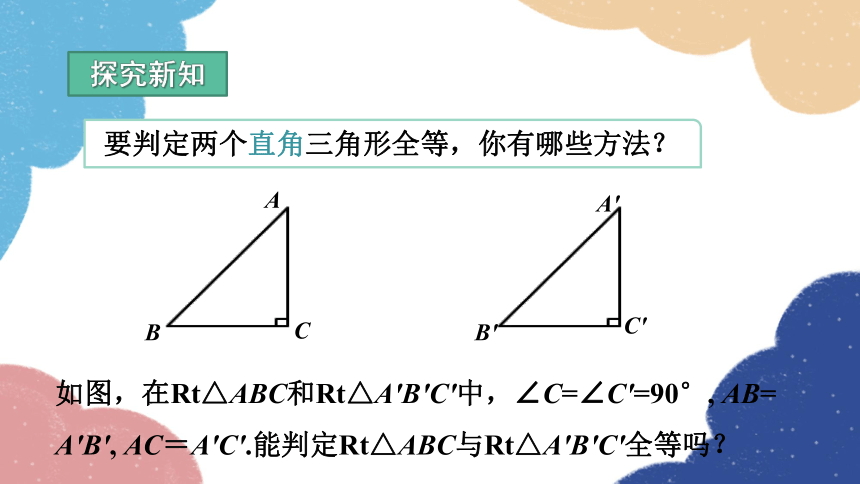
要判定两个直角三角形全等,你有哪些方法?
A
B
C
A′
B′
C′
如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°, AB=
A′B′, AC=A′C′.能判定Rt△ABC与Rt△A′B′C′全等吗?
A
B
C
A′
B′
C′
(A′)
(C′)
B′
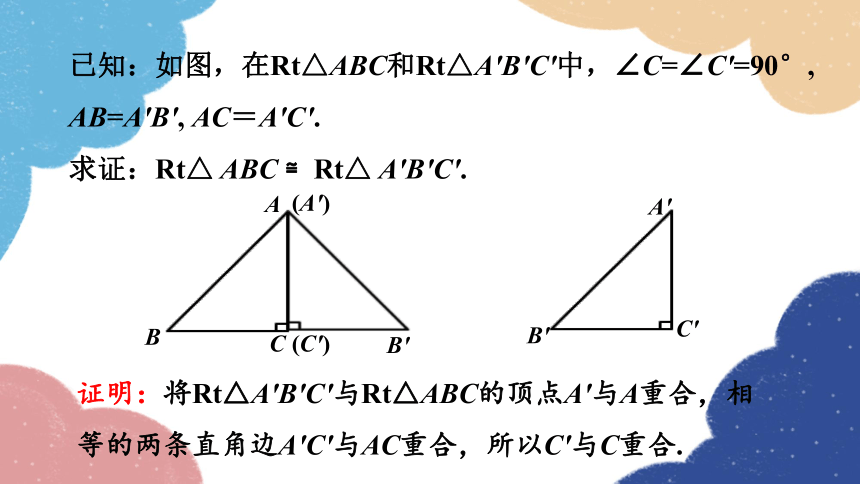
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°, AB=A′B′, AC=A′C′.
求证:Rt△ ABC ≌Rt△ A′B′C′.
证明:将Rt△A′B′C′与Rt△ABC的顶点A′与A重合,相等的两条直角边A′C′与AC重合,所以C′与C重合.
∵∠ACB=∠ A′B′C′ =90°,
∴点B,C,B′在同一条直线上,
∵在△ABB′中,AB=A′B,
∴ ∠B=∠B′.
又∵ AC=A′C′ ,
∴ Rt△ABC≌Rt△ A′B′C′ (AAS).
通过这个例子,你发现了什么?
直角三角形全等的判定定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
这个定理可以简单地记作“斜边、直角边”或“HL”.
由HL定理可知,两边及一角相等的两个三角形,当其中较大的一边的对角是直角是时,它们全等.
它有什么特点呢?
注意:
(1)“HL”是判定两个直角三角形全等的特殊方法,只适用于直角三角形全等的判定,对于一般三角形不适用,而前面学习的一般三角形全等的四种判定方法都可以在直角三角形中使用.
(2)在用一般方法证明时,由于两个直角三角形中已具备一对直角相等这一条件,故只需找到另外两个条件即可.
A
F
C
E
D
B
【例】AB=CD,BF⊥AC,DE⊥AC,AE=CF.
求证:BF=DE.
证明:在Rt△ABF和Rt△CDE中,
∵AE=CF,
∴AF=CE.
∵AB=CD,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
【例】已知:如下图,在△ABC中,D为BC的中点,DE⊥
AB于点E,DF⊥AC于点F,DE=DF.
求证:AD⊥BC.
证明:∵DE⊥AB,DF⊥AC(已知),
∴ ∠AED=∠DEB=∠AFD=∠DFC=90°
∵ D为BC的中点(已知),
∴ BD=DC(线段中点的定义).
在Rt△BED和Rt△CFD中,
∵BD=CD(已证),DE=DF(已知),
∴ Rt△BED≌Rt△CFD(HL),
∴ ∠B=∠C(全等三角形的对应角相等),
∴ AB=AC(有两个角相等的三角形是等腰三角形),
∴ AD⊥BC(等腰三角形“三线合一”).
课堂练习
1. 如图,在△ABC中,∠C=90°,DE⊥AB于点D,BC=BD,若AC=8 cm,则AE+DE=________cm.
分析:由 DE⊥AB知,∠BDE=90°,
所以∠BDE=∠C,又BC=BD,
所以△ BDE ≌△BCE(HL).
故DE=CE,AE+DE=AE+CE=AC=8 cm.
8
2.如图,Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交与点O,则有________ ≌_________,判定的根据是______.还有________≌________判断的根据是_______.
A
B
C
D
O
Rt△ABC
Rt△DCB
HL
Rt△ABO
Rt△DCO
ASA
3.已知:如下图,BE=CF,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F,且DB=DC.
求证:AD平分∠BAC.
证明:∵DE⊥AB,DF⊥AC(已知),
∴ ∠AED=∠CFD=90°(垂直的定义).
∴ △BDE与△CDF是直角三角形.
∵ BE=CF,BD=CD (已知) ,
∴ Rt△BDE≌Rt△CDF ( HL ).
∴ DE=DF(全等三角形的对应边相等).
∵ DE⊥AB,DF⊥AC(已知),
∴ AD平分∠BAC(角的内部到角的两边距离相等的点在这个角的平分线上).
证明一条射线是角的平分线时,通常转化为证明此射线上的点到角两边的距离相等.
课堂小结
直角三角形全等的判定定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
这个定理可以简单地记作“斜边、直角边”或“HL”.
谢谢!
第5章 几何证明初步
5.6 几何证明举例
第5课时 直角三角形全等的证明
学习目标
进一步熟悉证明题的题型,根据三角形全等推导“HL”定理;
熟练应用“斜边、直角边”定理及其它三角形全等的判定方法进行证明;
增强合作意识,提高逻辑思维能力.
复习导入
要判定两个三角形全等,你有哪些方法?
边角边 简称 “SAS”
角边角 简称 “ASA”
边边边 简称 “SSS”
角角边 简称 “AAS”
探究新知
要判定两个直角三角形全等,你有哪些方法?
A
B
C
A′
B′
C′
如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°, AB=
A′B′, AC=A′C′.能判定Rt△ABC与Rt△A′B′C′全等吗?
A
B
C
A′
B′
C′
(A′)
(C′)
B′
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°, AB=A′B′, AC=A′C′.
求证:Rt△ ABC ≌Rt△ A′B′C′.
证明:将Rt△A′B′C′与Rt△ABC的顶点A′与A重合,相等的两条直角边A′C′与AC重合,所以C′与C重合.
∵∠ACB=∠ A′B′C′ =90°,
∴点B,C,B′在同一条直线上,
∵在△ABB′中,AB=A′B,
∴ ∠B=∠B′.
又∵ AC=A′C′ ,
∴ Rt△ABC≌Rt△ A′B′C′ (AAS).
通过这个例子,你发现了什么?
直角三角形全等的判定定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
这个定理可以简单地记作“斜边、直角边”或“HL”.
由HL定理可知,两边及一角相等的两个三角形,当其中较大的一边的对角是直角是时,它们全等.
它有什么特点呢?
注意:
(1)“HL”是判定两个直角三角形全等的特殊方法,只适用于直角三角形全等的判定,对于一般三角形不适用,而前面学习的一般三角形全等的四种判定方法都可以在直角三角形中使用.
(2)在用一般方法证明时,由于两个直角三角形中已具备一对直角相等这一条件,故只需找到另外两个条件即可.
A
F
C
E
D
B
【例】AB=CD,BF⊥AC,DE⊥AC,AE=CF.
求证:BF=DE.
证明:在Rt△ABF和Rt△CDE中,
∵AE=CF,
∴AF=CE.
∵AB=CD,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
【例】已知:如下图,在△ABC中,D为BC的中点,DE⊥
AB于点E,DF⊥AC于点F,DE=DF.
求证:AD⊥BC.
证明:∵DE⊥AB,DF⊥AC(已知),
∴ ∠AED=∠DEB=∠AFD=∠DFC=90°
∵ D为BC的中点(已知),
∴ BD=DC(线段中点的定义).
在Rt△BED和Rt△CFD中,
∵BD=CD(已证),DE=DF(已知),
∴ Rt△BED≌Rt△CFD(HL),
∴ ∠B=∠C(全等三角形的对应角相等),
∴ AB=AC(有两个角相等的三角形是等腰三角形),
∴ AD⊥BC(等腰三角形“三线合一”).
课堂练习
1. 如图,在△ABC中,∠C=90°,DE⊥AB于点D,BC=BD,若AC=8 cm,则AE+DE=________cm.
分析:由 DE⊥AB知,∠BDE=90°,
所以∠BDE=∠C,又BC=BD,
所以△ BDE ≌△BCE(HL).
故DE=CE,AE+DE=AE+CE=AC=8 cm.
8
2.如图,Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交与点O,则有________ ≌_________,判定的根据是______.还有________≌________判断的根据是_______.
A
B
C
D
O
Rt△ABC
Rt△DCB
HL
Rt△ABO
Rt△DCO
ASA
3.已知:如下图,BE=CF,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F,且DB=DC.
求证:AD平分∠BAC.
证明:∵DE⊥AB,DF⊥AC(已知),
∴ ∠AED=∠CFD=90°(垂直的定义).
∴ △BDE与△CDF是直角三角形.
∵ BE=CF,BD=CD (已知) ,
∴ Rt△BDE≌Rt△CDF ( HL ).
∴ DE=DF(全等三角形的对应边相等).
∵ DE⊥AB,DF⊥AC(已知),
∴ AD平分∠BAC(角的内部到角的两边距离相等的点在这个角的平分线上).
证明一条射线是角的平分线时,通常转化为证明此射线上的点到角两边的距离相等.
课堂小结
直角三角形全等的判定定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
这个定理可以简单地记作“斜边、直角边”或“HL”.
谢谢!
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
