人教版数学八年级上册 周末培优二 (11.1-11.3)(含答案)
文档属性
| 名称 | 人教版数学八年级上册 周末培优二 (11.1-11.3)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 17:35:18 | ||
图片预览



文档简介
人教版数学八年级上册 周末培优二
(范围:11.1-11.3)
一、选择题
1.一个四边形截去一个角后,可以变成 ( )
A.三角形 B.四边形 C.五边形 D.以上都有可能
2.下列说法不正确的是 ( )
A.各边都相等的多边形是正多边形 B.正多边形的各边都相等
C.正三角形就是等边三角形 D.各内角相等的多边形不一定是正多边形
3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为 ( )
A.4,3 B.3,3 C.3,4 D.4,4
5.如图,在七边形ABCDEFG中,AB,ED的延长线相交于O点.若∠1+∠2+∠3+∠4=225°,则∠BOD的度数为 ( )
A.40° B.45° C.50° D.60°
第5题图 第6题图 第7题图
6.把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG= ( )
A.141° B.144° C.147° D.150°
7.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是 ( )
A.40° B.80° C.90° D.140°
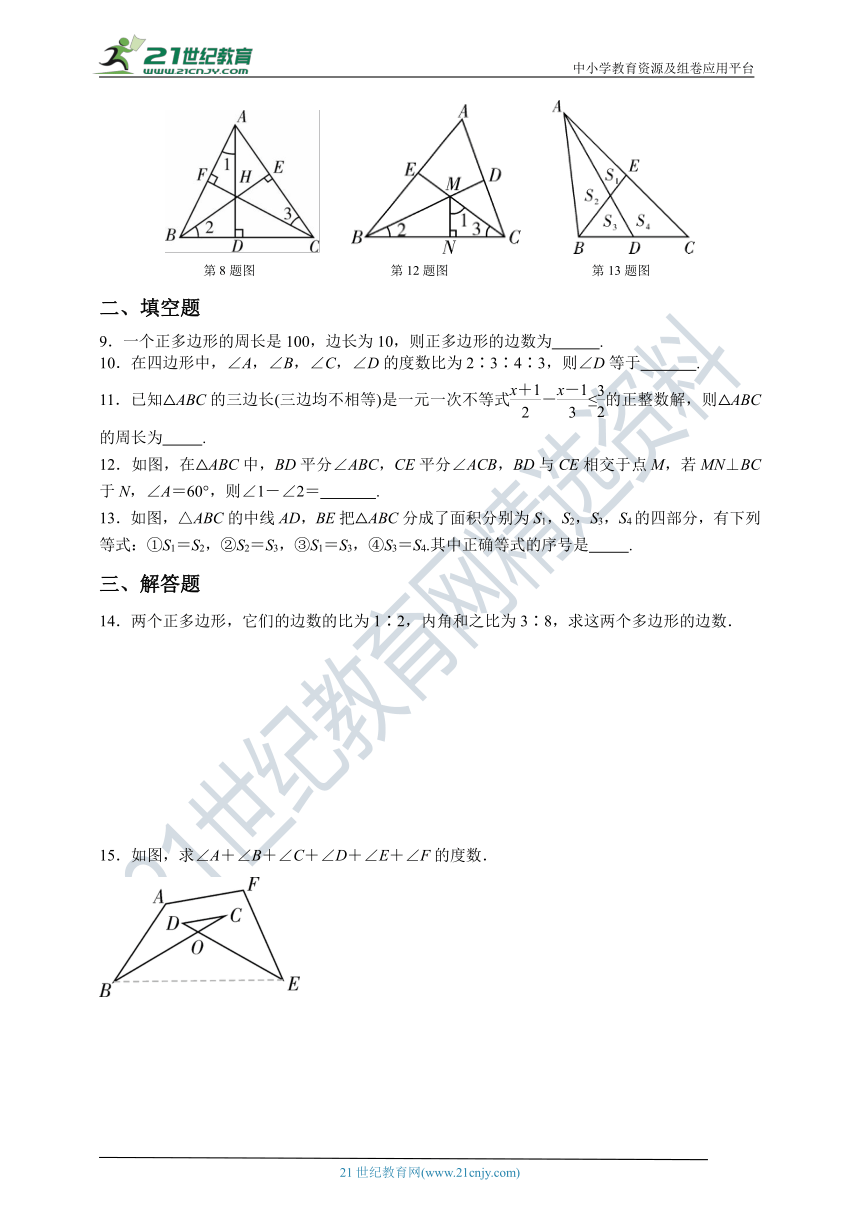
8.如图,△ABC的高AD,BE,CF相交于点H.有如下结论:
①图中能作为三角形的高的线段有6条;
②AD·BC=BE·AC=CF·AB;
③∠1+∠2+∠3=90°;
④∠CAD=∠CBE.
其中正确结论的个数有 ( )
A.1个 B.2个 C.3个 D.4个
第8题图 第12题图 第13题图
二、填空题
9.一个正多边形的周长是100,边长为10,则正多边形的边数为 .
10.在四边形中,∠A,∠B,∠C,∠D的度数比为2∶3∶4∶3,则∠D等于 .
11.已知△ABC的三边长(三边均不相等)是一元一次不等式-≤的正整数解,则△ABC的周长为 .
12.如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE相交于点M,若MN⊥BC于N,∠A=60°,则∠1-∠2= .
13.如图,△ABC的中线AD,BE把△ABC分成了面积分别为S1,S2,S3,S4的四部分,有下列等式:①S1=S2,②S2=S3,③S1=S3,④S3=S4.其中正确等式的序号是 .
三、解答题
14.两个正多边形,它们的边数的比为1∶2,内角和之比为3∶8,求这两个多边形的边数.
15.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
16.如图,在△ABC中,∠B=∠ACB,∠A=36°,线段CD和CE分别为△ABC的角平分线和高线,求∠ADC,∠DCE的大小.
17.小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.
(1)请用含m的式子表示第三条边长;
(2)第一条边长能否为10米?为什么?
(3)若第一条边长最短,求m的取值范围.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.一个四边形截去一个角后,可以变成 ( D )
A.三角形 B.四边形 C.五边形 D.以上都有可能
2.下列说法不正确的是 ( A )
A.各边都相等的多边形是正多边形 B.正多边形的各边都相等
C.正三角形就是等边三角形 D.各内角相等的多边形不一定是正多边形
3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( C )
A.108° B.90° C.72° D.60°
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为 ( C )
A.4,3 B.3,3 C.3,4 D.4,4
5.如图,在七边形ABCDEFG中,AB,ED的延长线相交于O点.若∠1+∠2+∠3+∠4=225°,则∠BOD的度数为 ( B )
A.40° B.45° C.50° D.60°
第5题图 第6题图 第7题图
6.把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG= ( B )
A.141° B.144° C.147° D.150°
7.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是 ( B )
A.40° B.80° C.90° D.140°
8.如图,△ABC的高AD,BE,CF相交于点H.有如下结论:
①图中能作为三角形的高的线段有6条;
②AD·BC=BE·AC=CF·AB;
③∠1+∠2+∠3=90°;
④∠CAD=∠CBE.
其中正确结论的个数有 ( C )
A.1个 B.2个 C.3个 D.4个
第8题图 第12题图 第13题图
二、填空题
9.一个正多边形的周长是100,边长为10,则正多边形的边数为 .
【答案】10
10.在四边形中,∠A,∠B,∠C,∠D的度数比为2∶3∶4∶3,则∠D等于 .
【答案】90°
11.已知△ABC的三边长(三边均不相等)是一元一次不等式-≤的正整数解,则△ABC的周长为 .
【答案】9
12.如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE相交于点M,若MN⊥BC于N,∠A=60°,则∠1-∠2= .
【答案】30°
13.如图,△ABC的中线AD,BE把△ABC分成了面积分别为S1,S2,S3,S4的四部分,有下列等式:①S1=S2,②S2=S3,③S1=S3,④S3=S4.其中正确等式的序号是 .
【答案】③
三、解答题
14.两个正多边形,它们的边数的比为1∶2,内角和之比为3∶8,求这两个多边形的边数.
解:设两个正多边形的边数分别为k,2k,
则其内角和分别为
(k-2)×180°,(2k-2)×180°,
根据题意列出方程得
[(k-2)×180°]∶[(2k-2)×180°]=3∶8,
解得k=5,∴2k=10.
∴这两个多边形的边数分别为5,10.
15.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
解:连接BE.
∵∠C+∠D+∠COD=180°,∠OBE+∠OEB+∠BOE=180°,
∠COD=∠BOE.
∴∠OBE+∠OEB=∠C+∠D,
∴∠A+∠ABC+∠C+∠D+∠FED+∠F
=∠A+∠ABC+∠OBE+∠OEB+∠FED+∠F=∠A+∠ABE+∠BEF+∠F=(4-2)×180°=360°.
16.如图,在△ABC中,∠B=∠ACB,∠A=36°,线段CD和CE分别为△ABC的角平分线和高线,求∠ADC,∠DCE的大小.
解:∵在△ABC中,
∠ACB=∠B,∠A=36°,
∴∠ACB=∠B=(180°-36°)=72°.
∵线段CD为△ABC的角平分线,
∴∠ACD=∠BCD=36°,
∴∠ADC=180°-∠A-∠ACD
=180°-36°-36°
=108°.
∵线段CE为△ABC的高线,
∴∠BEC=90°,
∴∠ECB=180°-∠B-∠BEC
=180°-72°-90°=18°,
∴∠DCE=∠DCB-∠BCE
=36°-18°=18°.
即∠ADC=108°,∠DCE=18°.
17.小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.
(1)请用含m的式子表示第三条边长;
解:∵第二条边长为(3m-2)米,
∴第三条边长为50-m-(3m-2)=(52-4m)米.
(2)第一条边长能否为10米?为什么?
解:当m=10时,三边长分别为10米,28米,12米,
∵10+12<28,
∴不能构成三角形,即第一条边长不能为10米.
(3)若第一条边长最短,求m的取值范围.
解:由题意得
解得<m<9.
(范围:11.1-11.3)
一、选择题
1.一个四边形截去一个角后,可以变成 ( )
A.三角形 B.四边形 C.五边形 D.以上都有可能
2.下列说法不正确的是 ( )
A.各边都相等的多边形是正多边形 B.正多边形的各边都相等
C.正三角形就是等边三角形 D.各内角相等的多边形不一定是正多边形
3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为 ( )
A.4,3 B.3,3 C.3,4 D.4,4
5.如图,在七边形ABCDEFG中,AB,ED的延长线相交于O点.若∠1+∠2+∠3+∠4=225°,则∠BOD的度数为 ( )
A.40° B.45° C.50° D.60°
第5题图 第6题图 第7题图
6.把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG= ( )
A.141° B.144° C.147° D.150°
7.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是 ( )
A.40° B.80° C.90° D.140°
8.如图,△ABC的高AD,BE,CF相交于点H.有如下结论:
①图中能作为三角形的高的线段有6条;
②AD·BC=BE·AC=CF·AB;
③∠1+∠2+∠3=90°;
④∠CAD=∠CBE.
其中正确结论的个数有 ( )
A.1个 B.2个 C.3个 D.4个
第8题图 第12题图 第13题图
二、填空题
9.一个正多边形的周长是100,边长为10,则正多边形的边数为 .
10.在四边形中,∠A,∠B,∠C,∠D的度数比为2∶3∶4∶3,则∠D等于 .
11.已知△ABC的三边长(三边均不相等)是一元一次不等式-≤的正整数解,则△ABC的周长为 .
12.如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE相交于点M,若MN⊥BC于N,∠A=60°,则∠1-∠2= .
13.如图,△ABC的中线AD,BE把△ABC分成了面积分别为S1,S2,S3,S4的四部分,有下列等式:①S1=S2,②S2=S3,③S1=S3,④S3=S4.其中正确等式的序号是 .
三、解答题
14.两个正多边形,它们的边数的比为1∶2,内角和之比为3∶8,求这两个多边形的边数.
15.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
16.如图,在△ABC中,∠B=∠ACB,∠A=36°,线段CD和CE分别为△ABC的角平分线和高线,求∠ADC,∠DCE的大小.
17.小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.
(1)请用含m的式子表示第三条边长;
(2)第一条边长能否为10米?为什么?
(3)若第一条边长最短,求m的取值范围.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.一个四边形截去一个角后,可以变成 ( D )
A.三角形 B.四边形 C.五边形 D.以上都有可能
2.下列说法不正确的是 ( A )
A.各边都相等的多边形是正多边形 B.正多边形的各边都相等
C.正三角形就是等边三角形 D.各内角相等的多边形不一定是正多边形
3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( C )
A.108° B.90° C.72° D.60°
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为 ( C )
A.4,3 B.3,3 C.3,4 D.4,4
5.如图,在七边形ABCDEFG中,AB,ED的延长线相交于O点.若∠1+∠2+∠3+∠4=225°,则∠BOD的度数为 ( B )
A.40° B.45° C.50° D.60°
第5题图 第6题图 第7题图
6.把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG= ( B )
A.141° B.144° C.147° D.150°
7.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是 ( B )
A.40° B.80° C.90° D.140°
8.如图,△ABC的高AD,BE,CF相交于点H.有如下结论:
①图中能作为三角形的高的线段有6条;
②AD·BC=BE·AC=CF·AB;
③∠1+∠2+∠3=90°;
④∠CAD=∠CBE.
其中正确结论的个数有 ( C )
A.1个 B.2个 C.3个 D.4个
第8题图 第12题图 第13题图
二、填空题
9.一个正多边形的周长是100,边长为10,则正多边形的边数为 .
【答案】10
10.在四边形中,∠A,∠B,∠C,∠D的度数比为2∶3∶4∶3,则∠D等于 .
【答案】90°
11.已知△ABC的三边长(三边均不相等)是一元一次不等式-≤的正整数解,则△ABC的周长为 .
【答案】9
12.如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE相交于点M,若MN⊥BC于N,∠A=60°,则∠1-∠2= .
【答案】30°
13.如图,△ABC的中线AD,BE把△ABC分成了面积分别为S1,S2,S3,S4的四部分,有下列等式:①S1=S2,②S2=S3,③S1=S3,④S3=S4.其中正确等式的序号是 .
【答案】③
三、解答题
14.两个正多边形,它们的边数的比为1∶2,内角和之比为3∶8,求这两个多边形的边数.
解:设两个正多边形的边数分别为k,2k,
则其内角和分别为
(k-2)×180°,(2k-2)×180°,
根据题意列出方程得
[(k-2)×180°]∶[(2k-2)×180°]=3∶8,
解得k=5,∴2k=10.
∴这两个多边形的边数分别为5,10.
15.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
解:连接BE.
∵∠C+∠D+∠COD=180°,∠OBE+∠OEB+∠BOE=180°,
∠COD=∠BOE.
∴∠OBE+∠OEB=∠C+∠D,
∴∠A+∠ABC+∠C+∠D+∠FED+∠F
=∠A+∠ABC+∠OBE+∠OEB+∠FED+∠F=∠A+∠ABE+∠BEF+∠F=(4-2)×180°=360°.
16.如图,在△ABC中,∠B=∠ACB,∠A=36°,线段CD和CE分别为△ABC的角平分线和高线,求∠ADC,∠DCE的大小.
解:∵在△ABC中,
∠ACB=∠B,∠A=36°,
∴∠ACB=∠B=(180°-36°)=72°.
∵线段CD为△ABC的角平分线,
∴∠ACD=∠BCD=36°,
∴∠ADC=180°-∠A-∠ACD
=180°-36°-36°
=108°.
∵线段CE为△ABC的高线,
∴∠BEC=90°,
∴∠ECB=180°-∠B-∠BEC
=180°-72°-90°=18°,
∴∠DCE=∠DCB-∠BCE
=36°-18°=18°.
即∠ADC=108°,∠DCE=18°.
17.小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.
(1)请用含m的式子表示第三条边长;
解:∵第二条边长为(3m-2)米,
∴第三条边长为50-m-(3m-2)=(52-4m)米.
(2)第一条边长能否为10米?为什么?
解:当m=10时,三边长分别为10米,28米,12米,
∵10+12<28,
∴不能构成三角形,即第一条边长不能为10米.
(3)若第一条边长最短,求m的取值范围.
解:由题意得
解得<m<9.
