人教版数学八年级上册 周末培优一 (11.1-11.2)(含答案)
文档属性
| 名称 | 人教版数学八年级上册 周末培优一 (11.1-11.2)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 17:39:29 | ||
图片预览



文档简介
人教版数学八年级上册 周末培优一
(范围:11.1-11.2)
一、选择题
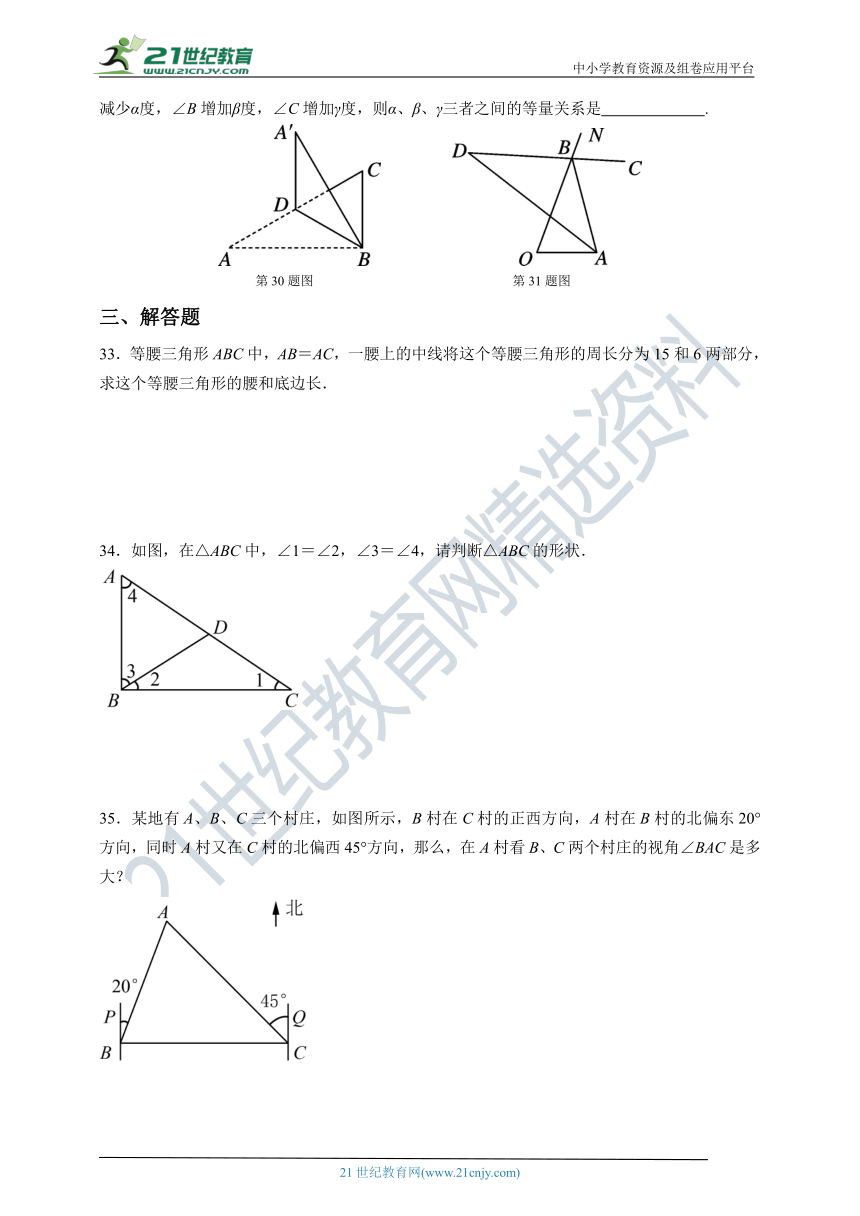
1.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( )
A.稳定性 B.灵活性 C.对称性 D.全等性
第1题图 第6题图 第7题图
2.(长沙中考)下列长度的三条线段,能组成三角形的是( )
A.4cm、5cm、9cm B.8cm、8cm、15cm
C.5cm、5cm、10cm D.6cm、7cm、14cm
3.已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )
A.11 B.5 C.2 D.1
4.以下列各组数据为边长,可以构成等腰三角形的是( )
A.2,3,4 B.5,5,10 C.2,2,1 D.1,2,3
5.具备下列条件的△ABC中,不为直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=∠C C.∠A=90°-∠B D.∠A-∠B=90°
6.(滨州期末)如图的图形中,三角形的个数为( )
A.3 B.4 C.5 D.6
7.如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
A.50° B.30° C.20° D.15°
8.30°角的直角三角尺与直线l1,l2的位置关系如图所示,已知l1∥l2,∠ACD=26°,则∠1的度数为( )
A.36° B.46° C.56° D.66°
第8题图 第9题图 第10题图
9.(广东中考)如图,AB∥CD,且∠DEC=100°,∠C=40°,则∠B的大小是( )
A.30° B.40° C.50° D.60°
10.如图,在△ABC中,BD⊥AC,EF∥AC,交BD于点G,那么下列结论错误的是( )
A.BD是△ABC的高 B.CD是△BCD的高 C.EG是△ABD的高 D.BG是△BEF的高
11.下图能说明∠1>∠2的是( )
12.△ABC的三个内角满足下列条件:
①∠A∶∠B∶∠C=3∶4∶5;②∠B+∠C=∠A;③∠A=2∠B=3∠C.
其中能判定△ABC是直角三角形的是( )
A.①②③ B.② C.①③ D.②③
13.如图是A,B,C三岛的平面图,B岛在A岛的西偏南40°方向,C岛在A岛的南偏东20°方向,C岛在B岛的北偏东80°方向,则从C岛看A,B两岛的视角∠ACB为( )
A.80° B.90° C.100° D.110°
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠B、∠C的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC等于( )
A.118° B.119° C.120° D.121°
15.如图所示,在△ABC中,E、F分别在边AB、AC上,则下列各式不能成立的是( )
A.∠BOC=∠2+∠6+∠A B.∠2=∠5-∠A
C.∠5=∠1+∠4 D.∠1=∠ABC+∠4
16.在△ABC中,∠A∶∠B∶∠C=3∶4∶5,则∠C等于( )
A.45° B.60° C.75° D.90°
17.如图,若量得∠B=∠C=∠D=∠E=35°,那么∠A等于( )
A.35° B.45° C.40° D.50°
第17题图 第18题图 第19题图
18.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,下列说法中,正确的个数为( )
①点A与点B的距离是线段AB的长;②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高;④线段CD是△BCD边BD上的高.
A.1个 B.2个 C.3个 D.4个
19.(黄石中考)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD等于( )
A.75° B.80° C.85° D.90°
二、填空题
20.如图:(1)在△ABC中,BC边上的高是 ;(2)在△AEC中,AE边上的高是 .
第20题图 第22题图 第25题图
21.(泰州中考)已知三角形两边的长分别为1、5,第三边的长为整数,则第三边的长为 .
22.如图所示,建高楼时常需用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?答: (填“稳定性”或“不稳定性”).
23.若a,b,c为三角形的三边,且a,b满足|a-9|+(b-2)2=0,第三边c为奇数,则c=___.
24.若直角三角形的两锐角之差为34°,则较大一个锐角的度数是_________.
25.如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板的另外一个角是 度.
26.(盐城中考)在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1= .
第26题图 第27题图 第28题图
27.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分面积是 .
28.如图,在△ABC中,D、E分别是BC、AD的中点,S△ABC=24cm2,则S△ABE= cm2.
29.若三角形的三边长是三个连续自然数,其周长m满足10<m<22,则这样的三角形有 个.
30.如图,△ABC中,∠C=60°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A′BD,此时A′D∥BC,则∠ABC=_________.
31.如图,在△OAB中,∠AOB=70°,∠OAB的平分线与△OAB的外角∠ABN的平分线所在的直线交于点D,则∠ADB的大小为_________.
32.在△ABC中,边BC不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减少α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是 .
第30题图 第31题图
三、解答题
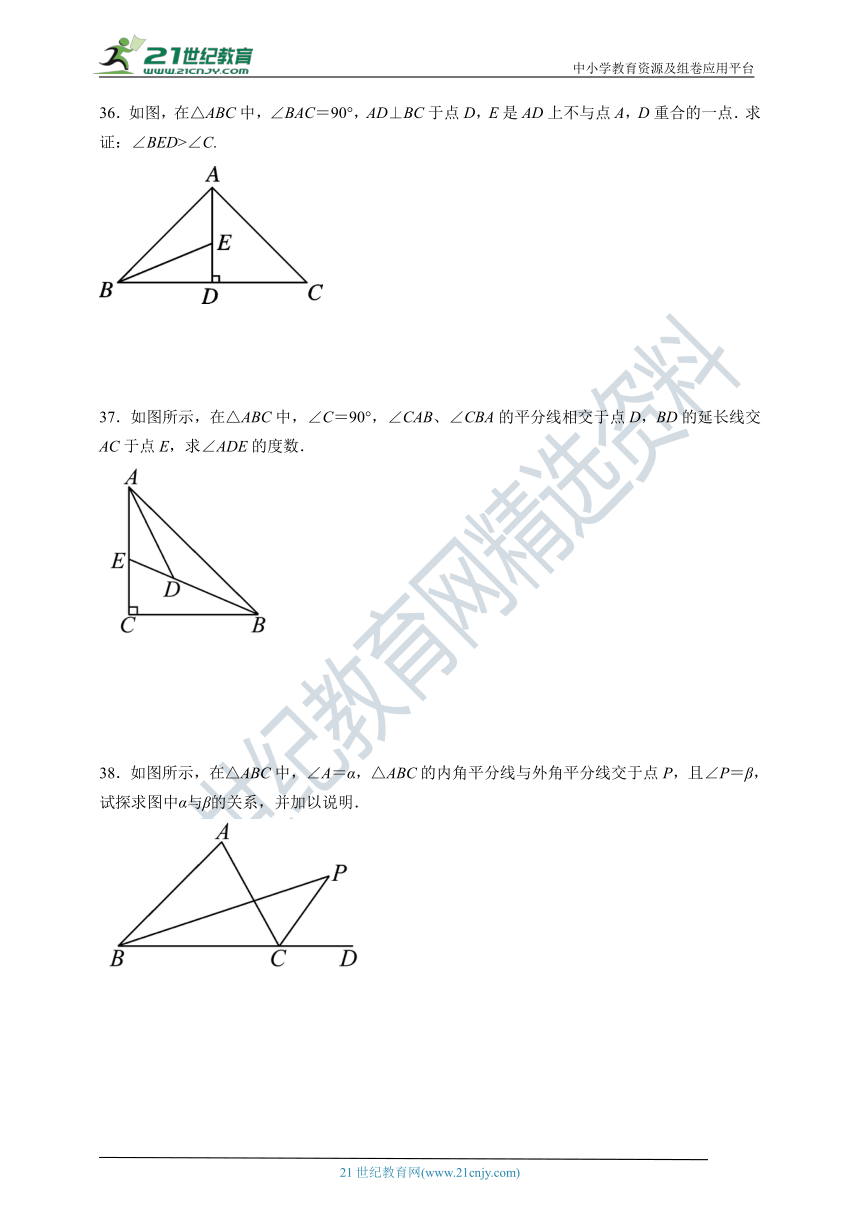
33.等腰三角形ABC中,AB=AC,一腰上的中线将这个等腰三角形的周长分为15和6两部分,求这个等腰三角形的腰和底边长.
34.如图,在△ABC中,∠1=∠2,∠3=∠4,请判断△ABC的形状.
35.某地有A、B、C三个村庄,如图所示,B村在C村的正西方向,A村在B村的北偏东20°方向,同时A村又在C村的北偏西45°方向,那么,在A村看B、C两个村庄的视角∠BAC是多大?
36.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上不与点A,D重合的一点.求证:∠BED>∠C.
37.如图所示,在△ABC中,∠C=90°,∠CAB、∠CBA的平分线相交于点D,BD的延长线交AC于点E,求∠ADE的度数.
38.如图所示,在△ABC中,∠A=α,△ABC的内角平分线与外角平分线交于点P,且∠P=β,试探求图中α与β的关系,并加以说明.
39.如图所示,(1)图中有几个三角形?请分别表示出来;
(2)∠AFC、∠ABD分别是哪些三角形的内角?
(3)以BD为边的三角形有哪些?
40.如图,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
41.如图,在△ABC中,点D,E分别在边AB,AC上,BE与CD交于点F,∠A=62°,∠ACD=25°,∠EFC=53°.求∠BDC和∠DBE的度数.
42.如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
43.用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵________.
∴ ∠BAE+∠1 +∠CBF+∠2+∠ACD+∠3=180°×3=540°.
∴ ∠BAE+∠CBF+∠ACD=540°-∠1-∠2-∠3,∵________.∴ ∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同方法完成证法2.
44.如图,BD平分∠OBC,AD平分∠OAC,∠C=80°,求∠D的大小.
45.如图,有一块含30°角的直角三角尺XYZ放置在△ABC中,三角尺的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角尺的位置,但仍使点B,C在三角尺的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
46.如图所示,BE与CD相交于点A,CF为∠BCD的角平分线,EF为∠BED的角平分线.
(1)试探求∠F与∠B、∠D间有何种等量关系;
(2)EF与FC能垂直吗?请给出证明;
(3)若∠B∶∠D∶∠F=2∶x∶3,求x的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( A )
A.稳定性 B.灵活性 C.对称性 D.全等性
第1题图 第6题图 第7题图
2.(长沙中考)下列长度的三条线段,能组成三角形的是( B )
A.4cm、5cm、9cm B.8cm、8cm、15cm
C.5cm、5cm、10cm D.6cm、7cm、14cm
3.已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( B )
A.11 B.5 C.2 D.1
4.以下列各组数据为边长,可以构成等腰三角形的是( C )
A.2,3,4 B.5,5,10 C.2,2,1 D.1,2,3
5.具备下列条件的△ABC中,不为直角三角形的是( D )
A.∠A+∠B=∠C B.∠A=∠B=∠C C.∠A=90°-∠B D.∠A-∠B=90°
6.(滨州期末)如图的图形中,三角形的个数为( C )
A.3 B.4 C.5 D.6
7.如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( C )
A.50° B.30° C.20° D.15°
8.30°角的直角三角尺与直线l1,l2的位置关系如图所示,已知l1∥l2,∠ACD=26°,则∠1的度数为( C )
A.36° B.46° C.56° D.66°
第8题图 第9题图 第10题图
9.(广东中考)如图,AB∥CD,且∠DEC=100°,∠C=40°,则∠B的大小是( B )
A.30° B.40° C.50° D.60°
10.如图,在△ABC中,BD⊥AC,EF∥AC,交BD于点G,那么下列结论错误的是( C )
A.BD是△ABC的高 B.CD是△BCD的高 C.EG是△ABD的高 D.BG是△BEF的高
11.下图能说明∠1>∠2的是( C )
12.△ABC的三个内角满足下列条件:
①∠A∶∠B∶∠C=3∶4∶5;②∠B+∠C=∠A;③∠A=2∠B=3∠C.
其中能判定△ABC是直角三角形的是( B )
A.①②③ B.② C.①③ D.②③
13.如图是A,B,C三岛的平面图,B岛在A岛的西偏南40°方向,C岛在A岛的南偏东20°方向,C岛在B岛的北偏东80°方向,则从C岛看A,B两岛的视角∠ACB为( A )
A.80° B.90° C.100° D.110°
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠B、∠C的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC等于( C )
A.118° B.119° C.120° D.121°
15.如图所示,在△ABC中,E、F分别在边AB、AC上,则下列各式不能成立的是( C )
A.∠BOC=∠2+∠6+∠A B.∠2=∠5-∠A
C.∠5=∠1+∠4 D.∠1=∠ABC+∠4
16.在△ABC中,∠A∶∠B∶∠C=3∶4∶5,则∠C等于( C )
A.45° B.60° C.75° D.90°
17.如图,若量得∠B=∠C=∠D=∠E=35°,那么∠A等于( C )
A.35° B.45° C.40° D.50°
第17题图 第18题图 第19题图
18.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,下列说法中,正确的个数为( D )
①点A与点B的距离是线段AB的长;②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高;④线段CD是△BCD边BD上的高.
A.1个 B.2个 C.3个 D.4个
19.(黄石中考)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD等于( A )
A.75° B.80° C.85° D.90°
【解析】 依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°,依据∠BAC=50°,AE平分∠BAC,即可得到∠DAE=5°,再根据△ABC中,∠C=180°-∠ABC-∠BAC=70°,可得∠EAD+∠ACD=75°.
二、填空题
20.如图:(1)在△ABC中,BC边上的高是 ;(2)在△AEC中,AE边上的高是 .
【答案】AB CD
第20题图 第22题图 第25题图
21.(泰州中考)已知三角形两边的长分别为1、5,第三边的长为整数,则第三边的长为 .
【答案】5
22.如图所示,建高楼时常需用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?答: (填“稳定性”或“不稳定性”).
【答案】稳定性
23.若a,b,c为三角形的三边,且a,b满足|a-9|+(b-2)2=0,第三边c为奇数,则c=___.
【答案】9
24.若直角三角形的两锐角之差为34°,则较大一个锐角的度数是_________.
【答案】62°
25.如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板的另外一个角是 度.
【答案】40
26.(盐城中考)在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1= .
【答案】120°
第26题图 第27题图 第28题图
27.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分面积是 .
【答案】4
28.如图,在△ABC中,D、E分别是BC、AD的中点,S△ABC=24cm2,则S△ABE= cm2.
【答案】6
29.若三角形的三边长是三个连续自然数,其周长m满足10<m<22,则这样的三角形有 个.
【答案】4
30.如图,△ABC中,∠C=60°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A′BD,此时A′D∥BC,则∠ABC=_________.
【答案】90°
第30题图 第31题图
31.如图,在△OAB中,∠AOB=70°,∠OAB的平分线与△OAB的外角∠ABN的平分线所在的直线交于点D,则∠ADB的大小为_________.
【答案】35°
32.在△ABC中,边BC不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减少α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是 .
【答案】α=β+γ
三、解答题
33.等腰三角形ABC中,AB=AC,一腰上的中线将这个等腰三角形的周长分为15和6两部分,求这个等腰三角形的腰和底边长.
解:设BD为中线.①若AB+AD=15,CD+BC=6,可得AB=AC=10,BC=1;②若AB+AD=6,BC+CD=15,可得AB=AC=4,BC=13.∵4+4<13,∴不合题意.故腰长为10,底边为1.
34.如图,在△ABC中,∠1=∠2,∠3=∠4,请判断△ABC的形状.
解:在△ABC中,∠1+∠2+∠3+∠4=180°,∵∠1=∠2,∠3=∠4,∴∠2+∠3=×180°=90°,即∠ABC=90°,∴△ABC是直角三角形.
35.某地有A、B、C三个村庄,如图所示,B村在C村的正西方向,A村在B村的北偏东20°方向,同时A村又在C村的北偏西45°方向,那么,在A村看B、C两个村庄的视角∠BAC是多大?
解:由A村在B村的北偏东20°,得∠ABC=∠PBC-∠PBA=90°-20°=70°.由A村在C村的北偏西45°方向,得∠ACB=∠QCB-∠QCA=90°-45°=45°.∴∠BAC=180°-∠ABC-∠ACB=180°-70°-45°=65°.∴在A村看B、C两个村庄的视角∠BAC是65°.
36.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上不与点A,D重合的一点.求证:∠BED>∠C.
证明:∵∠BAC=90°,AD⊥BC,
∴∠BAE+∠DAC=90°,
∠C+∠DAC=90°,
∴∠C=∠BAE.
∵∠BED为△ABE的外角,
∴∠BED>∠BAE,
∴∠BED>∠C.
37.如图所示,在△ABC中,∠C=90°,∠CAB、∠CBA的平分线相交于点D,BD的延长线交AC于点E,求∠ADE的度数.
解:∵∠C=90°,∴∠CAB+∠CBA=90°,又∵AD平分∠CAB,BD平分∠CBA,∴∠BAD=∠BAC,∠DBA=∠CBA,∴∠BAD+∠DBA=×90°=45°,∴∠ADB=180°-(∠BAD+∠DBA)=135°,∴∠ADE=180°-∠ADB=45°.
38.如图所示,在△ABC中,∠A=α,△ABC的内角平分线与外角平分线交于点P,且∠P=β,试探求图中α与β的关系,并加以说明.
解:β=α.因为∠P=∠PCD-∠PBC,而∠PCD=∠ACD,∠PBC=∠ABC,所以∠P=∠ACD-∠ABC=(∠ACD-∠ABC)=∠A,即β=α.
39.如图所示,(1)图中有几个三角形?请分别表示出来;
(2)∠AFC、∠ABD分别是哪些三角形的内角?
(3)以BD为边的三角形有哪些?
解:(1)图中共有8个三角形,分别是△ABD、△ACF、
△ABC、△DBC、△DEC、△CBE、△CBF、△BEF;
(2)∠AFC是△AFC的内角,∠ABD是△ABD和△BEF的内角;
(3)以BD为边的三角形有△ABD和△BDC.
40.如图,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
解:(1)∵∠B=66°,∠C=54°,∴∠BAC=180°-∠B-∠C=60°.又∵AD平分∠BAC,∴∠BAD=∠CAD=∠BAC=30°,∴∠ADB=180°-∠B-∠BAD=180°-66°-30°=84°,∠ADC=∠B+∠BAD=66°+30°=96°;
(2)∵DE⊥AC,∴∠EDC=90°-∠C=36°,∴∠ADE=∠ADC-∠EDC=96°-36°=60°.
41.如图,在△ABC中,点D,E分别在边AB,AC上,BE与CD交于点F,∠A=62°,∠ACD=25°,∠EFC=53°.求∠BDC和∠DBE的度数.
解:∵∠A=62°,∠ACD=25°,
∴∠BDC=∠A+∠ACD=62°+25°=87°.
∵∠EFC=∠DFB=53°,
∴∠DBE=180°-∠BDC-∠DFB=40°.
42.如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
解:∵AD是BC边上的中线,AC=2BC,∴BD=CD,设BD=CD=x,AB=y,则AC=4x,分为两种情况:①AC+CD=60,AB+BD=40,则4x+x=60,x+y=40,解得:x=12,y=28,即AC=4x=48,AB=28;②AC+CD=40,AB+BD=60,则4x+x=40,x+y=60,解得:x=8,y=52,即AC=4x=32,AB=52,BC=2x=16,此时不符合三角形三边关系定理,综合上述:AC=48,AB=28.
43.用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵________.
∴ ∠BAE+∠1 +∠CBF+∠2+∠ACD+∠3=180°×3=540°.
∴ ∠BAE+∠CBF+∠ACD=540°-∠1-∠2-∠3,∵________.∴ ∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同方法完成证法2.
解:∠BAE+∠1=∠CBF+∠2=∠ACD+∠3=180°. ∠1+∠2+∠3=180°. 证法2:过点A作射线AP,使AP∥BD. ∵ AP∥BD,∴ ∠CBF=∠PAB,∠ACD=∠EAP.∵∠BAE+∠PAB+∠EAP=360°,∴∠BAE+∠CBF+∠ACD=360°.
44.如图,BD平分∠OBC,AD平分∠OAC,∠C=80°,求∠D的大小.
解:设BC交y轴于点E,由△OBE与△ACE为对顶三角形知,∠CAE+∠C=∠OBE+∠BOE,
即2∠1+∠C=2∠2+90°,
∴∠1-∠2=5°.
同理可得∠1+∠D=∠2+∠BOE,
即∠D=∠2-∠1+90°=90°-5°=85°.
45.如图,有一块含30°角的直角三角尺XYZ放置在△ABC中,三角尺的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角尺的位置,但仍使点B,C在三角尺的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
解:(1)60°.
(2)∠ABX+∠ACX的大小没有变化.理由如下:
∵∠ABC+∠ACB=180°-∠A,∠YXZ=90°,
∴∠XBC+∠XCB=90°.
∴∠ABX+∠ACX=180°-∠A-90°=90°-∠A.
即∠ABX+∠ACX的大小没有变化.
46.如图所示,BE与CD相交于点A,CF为∠BCD的角平分线,EF为∠BED的角平分线.
(1)试探求∠F与∠B、∠D间有何种等量关系;
(2)EF与FC能垂直吗?请给出证明;
(3)若∠B∶∠D∶∠F=2∶x∶3,求x的值.
解:(1)∠D+∠B=2∠F;
(2)能.理由:若EF与FC垂直,即∠F=90°,则∠B+∠D=180°,也就是说,如果∠D与∠B互补,则EF⊥FC; (3)∵∠B∶∠D∶∠F=2∶x∶3,∴设∠B=2k,∠D=xk,∠F=3k,由(1)得xk+2k=6k,∴x=4.
(范围:11.1-11.2)
一、选择题
1.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( )
A.稳定性 B.灵活性 C.对称性 D.全等性
第1题图 第6题图 第7题图
2.(长沙中考)下列长度的三条线段,能组成三角形的是( )
A.4cm、5cm、9cm B.8cm、8cm、15cm
C.5cm、5cm、10cm D.6cm、7cm、14cm
3.已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )
A.11 B.5 C.2 D.1
4.以下列各组数据为边长,可以构成等腰三角形的是( )
A.2,3,4 B.5,5,10 C.2,2,1 D.1,2,3
5.具备下列条件的△ABC中,不为直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=∠C C.∠A=90°-∠B D.∠A-∠B=90°
6.(滨州期末)如图的图形中,三角形的个数为( )
A.3 B.4 C.5 D.6
7.如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
A.50° B.30° C.20° D.15°
8.30°角的直角三角尺与直线l1,l2的位置关系如图所示,已知l1∥l2,∠ACD=26°,则∠1的度数为( )
A.36° B.46° C.56° D.66°
第8题图 第9题图 第10题图
9.(广东中考)如图,AB∥CD,且∠DEC=100°,∠C=40°,则∠B的大小是( )
A.30° B.40° C.50° D.60°
10.如图,在△ABC中,BD⊥AC,EF∥AC,交BD于点G,那么下列结论错误的是( )
A.BD是△ABC的高 B.CD是△BCD的高 C.EG是△ABD的高 D.BG是△BEF的高
11.下图能说明∠1>∠2的是( )
12.△ABC的三个内角满足下列条件:
①∠A∶∠B∶∠C=3∶4∶5;②∠B+∠C=∠A;③∠A=2∠B=3∠C.
其中能判定△ABC是直角三角形的是( )
A.①②③ B.② C.①③ D.②③
13.如图是A,B,C三岛的平面图,B岛在A岛的西偏南40°方向,C岛在A岛的南偏东20°方向,C岛在B岛的北偏东80°方向,则从C岛看A,B两岛的视角∠ACB为( )
A.80° B.90° C.100° D.110°
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠B、∠C的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC等于( )
A.118° B.119° C.120° D.121°
15.如图所示,在△ABC中,E、F分别在边AB、AC上,则下列各式不能成立的是( )
A.∠BOC=∠2+∠6+∠A B.∠2=∠5-∠A
C.∠5=∠1+∠4 D.∠1=∠ABC+∠4
16.在△ABC中,∠A∶∠B∶∠C=3∶4∶5,则∠C等于( )
A.45° B.60° C.75° D.90°
17.如图,若量得∠B=∠C=∠D=∠E=35°,那么∠A等于( )
A.35° B.45° C.40° D.50°
第17题图 第18题图 第19题图
18.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,下列说法中,正确的个数为( )
①点A与点B的距离是线段AB的长;②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高;④线段CD是△BCD边BD上的高.
A.1个 B.2个 C.3个 D.4个
19.(黄石中考)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD等于( )
A.75° B.80° C.85° D.90°
二、填空题
20.如图:(1)在△ABC中,BC边上的高是 ;(2)在△AEC中,AE边上的高是 .
第20题图 第22题图 第25题图
21.(泰州中考)已知三角形两边的长分别为1、5,第三边的长为整数,则第三边的长为 .
22.如图所示,建高楼时常需用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?答: (填“稳定性”或“不稳定性”).
23.若a,b,c为三角形的三边,且a,b满足|a-9|+(b-2)2=0,第三边c为奇数,则c=___.
24.若直角三角形的两锐角之差为34°,则较大一个锐角的度数是_________.
25.如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板的另外一个角是 度.
26.(盐城中考)在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1= .
第26题图 第27题图 第28题图
27.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分面积是 .
28.如图,在△ABC中,D、E分别是BC、AD的中点,S△ABC=24cm2,则S△ABE= cm2.
29.若三角形的三边长是三个连续自然数,其周长m满足10<m<22,则这样的三角形有 个.
30.如图,△ABC中,∠C=60°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A′BD,此时A′D∥BC,则∠ABC=_________.
31.如图,在△OAB中,∠AOB=70°,∠OAB的平分线与△OAB的外角∠ABN的平分线所在的直线交于点D,则∠ADB的大小为_________.
32.在△ABC中,边BC不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减少α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是 .
第30题图 第31题图
三、解答题
33.等腰三角形ABC中,AB=AC,一腰上的中线将这个等腰三角形的周长分为15和6两部分,求这个等腰三角形的腰和底边长.
34.如图,在△ABC中,∠1=∠2,∠3=∠4,请判断△ABC的形状.
35.某地有A、B、C三个村庄,如图所示,B村在C村的正西方向,A村在B村的北偏东20°方向,同时A村又在C村的北偏西45°方向,那么,在A村看B、C两个村庄的视角∠BAC是多大?
36.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上不与点A,D重合的一点.求证:∠BED>∠C.
37.如图所示,在△ABC中,∠C=90°,∠CAB、∠CBA的平分线相交于点D,BD的延长线交AC于点E,求∠ADE的度数.
38.如图所示,在△ABC中,∠A=α,△ABC的内角平分线与外角平分线交于点P,且∠P=β,试探求图中α与β的关系,并加以说明.
39.如图所示,(1)图中有几个三角形?请分别表示出来;
(2)∠AFC、∠ABD分别是哪些三角形的内角?
(3)以BD为边的三角形有哪些?
40.如图,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
41.如图,在△ABC中,点D,E分别在边AB,AC上,BE与CD交于点F,∠A=62°,∠ACD=25°,∠EFC=53°.求∠BDC和∠DBE的度数.
42.如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
43.用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵________.
∴ ∠BAE+∠1 +∠CBF+∠2+∠ACD+∠3=180°×3=540°.
∴ ∠BAE+∠CBF+∠ACD=540°-∠1-∠2-∠3,∵________.∴ ∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同方法完成证法2.
44.如图,BD平分∠OBC,AD平分∠OAC,∠C=80°,求∠D的大小.
45.如图,有一块含30°角的直角三角尺XYZ放置在△ABC中,三角尺的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角尺的位置,但仍使点B,C在三角尺的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
46.如图所示,BE与CD相交于点A,CF为∠BCD的角平分线,EF为∠BED的角平分线.
(1)试探求∠F与∠B、∠D间有何种等量关系;
(2)EF与FC能垂直吗?请给出证明;
(3)若∠B∶∠D∶∠F=2∶x∶3,求x的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( A )
A.稳定性 B.灵活性 C.对称性 D.全等性
第1题图 第6题图 第7题图
2.(长沙中考)下列长度的三条线段,能组成三角形的是( B )
A.4cm、5cm、9cm B.8cm、8cm、15cm
C.5cm、5cm、10cm D.6cm、7cm、14cm
3.已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( B )
A.11 B.5 C.2 D.1
4.以下列各组数据为边长,可以构成等腰三角形的是( C )
A.2,3,4 B.5,5,10 C.2,2,1 D.1,2,3
5.具备下列条件的△ABC中,不为直角三角形的是( D )
A.∠A+∠B=∠C B.∠A=∠B=∠C C.∠A=90°-∠B D.∠A-∠B=90°
6.(滨州期末)如图的图形中,三角形的个数为( C )
A.3 B.4 C.5 D.6
7.如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( C )
A.50° B.30° C.20° D.15°
8.30°角的直角三角尺与直线l1,l2的位置关系如图所示,已知l1∥l2,∠ACD=26°,则∠1的度数为( C )
A.36° B.46° C.56° D.66°
第8题图 第9题图 第10题图
9.(广东中考)如图,AB∥CD,且∠DEC=100°,∠C=40°,则∠B的大小是( B )
A.30° B.40° C.50° D.60°
10.如图,在△ABC中,BD⊥AC,EF∥AC,交BD于点G,那么下列结论错误的是( C )
A.BD是△ABC的高 B.CD是△BCD的高 C.EG是△ABD的高 D.BG是△BEF的高
11.下图能说明∠1>∠2的是( C )
12.△ABC的三个内角满足下列条件:
①∠A∶∠B∶∠C=3∶4∶5;②∠B+∠C=∠A;③∠A=2∠B=3∠C.
其中能判定△ABC是直角三角形的是( B )
A.①②③ B.② C.①③ D.②③
13.如图是A,B,C三岛的平面图,B岛在A岛的西偏南40°方向,C岛在A岛的南偏东20°方向,C岛在B岛的北偏东80°方向,则从C岛看A,B两岛的视角∠ACB为( A )
A.80° B.90° C.100° D.110°
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠B、∠C的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC等于( C )
A.118° B.119° C.120° D.121°
15.如图所示,在△ABC中,E、F分别在边AB、AC上,则下列各式不能成立的是( C )
A.∠BOC=∠2+∠6+∠A B.∠2=∠5-∠A
C.∠5=∠1+∠4 D.∠1=∠ABC+∠4
16.在△ABC中,∠A∶∠B∶∠C=3∶4∶5,则∠C等于( C )
A.45° B.60° C.75° D.90°
17.如图,若量得∠B=∠C=∠D=∠E=35°,那么∠A等于( C )
A.35° B.45° C.40° D.50°
第17题图 第18题图 第19题图
18.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,下列说法中,正确的个数为( D )
①点A与点B的距离是线段AB的长;②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高;④线段CD是△BCD边BD上的高.
A.1个 B.2个 C.3个 D.4个
19.(黄石中考)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD等于( A )
A.75° B.80° C.85° D.90°
【解析】 依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°,依据∠BAC=50°,AE平分∠BAC,即可得到∠DAE=5°,再根据△ABC中,∠C=180°-∠ABC-∠BAC=70°,可得∠EAD+∠ACD=75°.
二、填空题
20.如图:(1)在△ABC中,BC边上的高是 ;(2)在△AEC中,AE边上的高是 .
【答案】AB CD
第20题图 第22题图 第25题图
21.(泰州中考)已知三角形两边的长分别为1、5,第三边的长为整数,则第三边的长为 .
【答案】5
22.如图所示,建高楼时常需用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?答: (填“稳定性”或“不稳定性”).
【答案】稳定性
23.若a,b,c为三角形的三边,且a,b满足|a-9|+(b-2)2=0,第三边c为奇数,则c=___.
【答案】9
24.若直角三角形的两锐角之差为34°,则较大一个锐角的度数是_________.
【答案】62°
25.如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板的另外一个角是 度.
【答案】40
26.(盐城中考)在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1= .
【答案】120°
第26题图 第27题图 第28题图
27.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分面积是 .
【答案】4
28.如图,在△ABC中,D、E分别是BC、AD的中点,S△ABC=24cm2,则S△ABE= cm2.
【答案】6
29.若三角形的三边长是三个连续自然数,其周长m满足10<m<22,则这样的三角形有 个.
【答案】4
30.如图,△ABC中,∠C=60°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A′BD,此时A′D∥BC,则∠ABC=_________.
【答案】90°
第30题图 第31题图
31.如图,在△OAB中,∠AOB=70°,∠OAB的平分线与△OAB的外角∠ABN的平分线所在的直线交于点D,则∠ADB的大小为_________.
【答案】35°
32.在△ABC中,边BC不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减少α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是 .
【答案】α=β+γ
三、解答题
33.等腰三角形ABC中,AB=AC,一腰上的中线将这个等腰三角形的周长分为15和6两部分,求这个等腰三角形的腰和底边长.
解:设BD为中线.①若AB+AD=15,CD+BC=6,可得AB=AC=10,BC=1;②若AB+AD=6,BC+CD=15,可得AB=AC=4,BC=13.∵4+4<13,∴不合题意.故腰长为10,底边为1.
34.如图,在△ABC中,∠1=∠2,∠3=∠4,请判断△ABC的形状.
解:在△ABC中,∠1+∠2+∠3+∠4=180°,∵∠1=∠2,∠3=∠4,∴∠2+∠3=×180°=90°,即∠ABC=90°,∴△ABC是直角三角形.
35.某地有A、B、C三个村庄,如图所示,B村在C村的正西方向,A村在B村的北偏东20°方向,同时A村又在C村的北偏西45°方向,那么,在A村看B、C两个村庄的视角∠BAC是多大?
解:由A村在B村的北偏东20°,得∠ABC=∠PBC-∠PBA=90°-20°=70°.由A村在C村的北偏西45°方向,得∠ACB=∠QCB-∠QCA=90°-45°=45°.∴∠BAC=180°-∠ABC-∠ACB=180°-70°-45°=65°.∴在A村看B、C两个村庄的视角∠BAC是65°.
36.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上不与点A,D重合的一点.求证:∠BED>∠C.
证明:∵∠BAC=90°,AD⊥BC,
∴∠BAE+∠DAC=90°,
∠C+∠DAC=90°,
∴∠C=∠BAE.
∵∠BED为△ABE的外角,
∴∠BED>∠BAE,
∴∠BED>∠C.
37.如图所示,在△ABC中,∠C=90°,∠CAB、∠CBA的平分线相交于点D,BD的延长线交AC于点E,求∠ADE的度数.
解:∵∠C=90°,∴∠CAB+∠CBA=90°,又∵AD平分∠CAB,BD平分∠CBA,∴∠BAD=∠BAC,∠DBA=∠CBA,∴∠BAD+∠DBA=×90°=45°,∴∠ADB=180°-(∠BAD+∠DBA)=135°,∴∠ADE=180°-∠ADB=45°.
38.如图所示,在△ABC中,∠A=α,△ABC的内角平分线与外角平分线交于点P,且∠P=β,试探求图中α与β的关系,并加以说明.
解:β=α.因为∠P=∠PCD-∠PBC,而∠PCD=∠ACD,∠PBC=∠ABC,所以∠P=∠ACD-∠ABC=(∠ACD-∠ABC)=∠A,即β=α.
39.如图所示,(1)图中有几个三角形?请分别表示出来;
(2)∠AFC、∠ABD分别是哪些三角形的内角?
(3)以BD为边的三角形有哪些?
解:(1)图中共有8个三角形,分别是△ABD、△ACF、
△ABC、△DBC、△DEC、△CBE、△CBF、△BEF;
(2)∠AFC是△AFC的内角,∠ABD是△ABD和△BEF的内角;
(3)以BD为边的三角形有△ABD和△BDC.
40.如图,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
解:(1)∵∠B=66°,∠C=54°,∴∠BAC=180°-∠B-∠C=60°.又∵AD平分∠BAC,∴∠BAD=∠CAD=∠BAC=30°,∴∠ADB=180°-∠B-∠BAD=180°-66°-30°=84°,∠ADC=∠B+∠BAD=66°+30°=96°;
(2)∵DE⊥AC,∴∠EDC=90°-∠C=36°,∴∠ADE=∠ADC-∠EDC=96°-36°=60°.
41.如图,在△ABC中,点D,E分别在边AB,AC上,BE与CD交于点F,∠A=62°,∠ACD=25°,∠EFC=53°.求∠BDC和∠DBE的度数.
解:∵∠A=62°,∠ACD=25°,
∴∠BDC=∠A+∠ACD=62°+25°=87°.
∵∠EFC=∠DFB=53°,
∴∠DBE=180°-∠BDC-∠DFB=40°.
42.如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
解:∵AD是BC边上的中线,AC=2BC,∴BD=CD,设BD=CD=x,AB=y,则AC=4x,分为两种情况:①AC+CD=60,AB+BD=40,则4x+x=60,x+y=40,解得:x=12,y=28,即AC=4x=48,AB=28;②AC+CD=40,AB+BD=60,则4x+x=40,x+y=60,解得:x=8,y=52,即AC=4x=32,AB=52,BC=2x=16,此时不符合三角形三边关系定理,综合上述:AC=48,AB=28.
43.用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵________.
∴ ∠BAE+∠1 +∠CBF+∠2+∠ACD+∠3=180°×3=540°.
∴ ∠BAE+∠CBF+∠ACD=540°-∠1-∠2-∠3,∵________.∴ ∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同方法完成证法2.
解:∠BAE+∠1=∠CBF+∠2=∠ACD+∠3=180°. ∠1+∠2+∠3=180°. 证法2:过点A作射线AP,使AP∥BD. ∵ AP∥BD,∴ ∠CBF=∠PAB,∠ACD=∠EAP.∵∠BAE+∠PAB+∠EAP=360°,∴∠BAE+∠CBF+∠ACD=360°.
44.如图,BD平分∠OBC,AD平分∠OAC,∠C=80°,求∠D的大小.
解:设BC交y轴于点E,由△OBE与△ACE为对顶三角形知,∠CAE+∠C=∠OBE+∠BOE,
即2∠1+∠C=2∠2+90°,
∴∠1-∠2=5°.
同理可得∠1+∠D=∠2+∠BOE,
即∠D=∠2-∠1+90°=90°-5°=85°.
45.如图,有一块含30°角的直角三角尺XYZ放置在△ABC中,三角尺的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角尺的位置,但仍使点B,C在三角尺的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
解:(1)60°.
(2)∠ABX+∠ACX的大小没有变化.理由如下:
∵∠ABC+∠ACB=180°-∠A,∠YXZ=90°,
∴∠XBC+∠XCB=90°.
∴∠ABX+∠ACX=180°-∠A-90°=90°-∠A.
即∠ABX+∠ACX的大小没有变化.
46.如图所示,BE与CD相交于点A,CF为∠BCD的角平分线,EF为∠BED的角平分线.
(1)试探求∠F与∠B、∠D间有何种等量关系;
(2)EF与FC能垂直吗?请给出证明;
(3)若∠B∶∠D∶∠F=2∶x∶3,求x的值.
解:(1)∠D+∠B=2∠F;
(2)能.理由:若EF与FC垂直,即∠F=90°,则∠B+∠D=180°,也就是说,如果∠D与∠B互补,则EF⊥FC; (3)∵∠B∶∠D∶∠F=2∶x∶3,∴设∠B=2k,∠D=xk,∠F=3k,由(1)得xk+2k=6k,∴x=4.
