4.3 角 同步练习 (含解析)2022-2023学年上学期广西各地七年级数学期末试题选编
文档属性
| 名称 | 4.3 角 同步练习 (含解析)2022-2023学年上学期广西各地七年级数学期末试题选编 |  | |
| 格式 | docx | ||
| 文件大小 | 782.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 15:53:30 | ||
图片预览




文档简介
4.3 角
一、单选题
1.(2022秋·广西贺州·七年级统考期末)如图,从的顶点引出两条射线OC,OD,图中的角共有( )
A.3个 B.4个 C.6个 D.7个
2.(2022秋·广西河池·七年级统考期末)下列四个图中,能用三种方法表示同一个角的是( )
A. B.
C. D.
3.(2022秋·广西崇左·七年级统考期末)如图,从8点钟开始,过了20分钟后,分针与时针所夹的度数是( )
A. B. C. D.
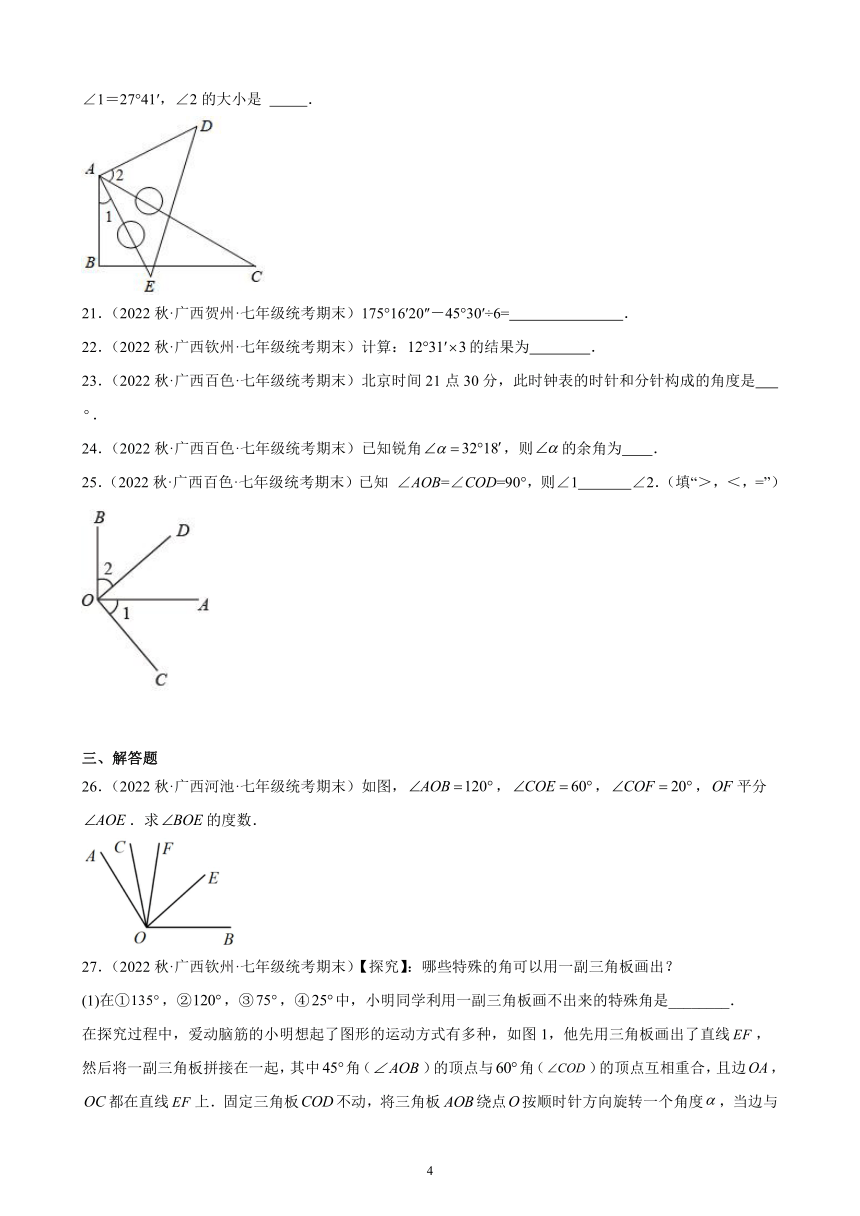
4.(2022秋·广西防城港·七年级统考期末)某测绘装置上一枚指针原来指向南偏西50°(如图),把这枚指针按逆时针方向旋转周,则结果指针的指向( )
A.南偏东50° B.西偏北50° C.南偏东40° D.东南方向
5.(2022秋·广西柳州·七年级统考期末)点看点的方向是北偏东,那么点看点的方向是( )
A.南偏东 B.南偏西 C.南偏东 D.南偏西
6.(2022秋·广西桂林·七年级统考期末)下列各角中,为锐角的是( )
A.平角 B.周角 C.直角 D.周角
7.(2022秋·广西钦州·七年级统考期末)把两块三角板按如图所示那样拼在一起,则∠ABC等于( )
A.70° B.90° C.105° D.120°
8.(2022春·广西玉林·七年级统考期末)如图,已知//,平分,平分.若,则的度数为( )(注:四边形内角和等于)
A. B. C. D.
9.(2022秋·广西贺州·七年级统考期末)一个角的度数是,则这个角的余角是( )
A. B. C. D.
10.(2022秋·广西崇左·七年级统考期末)若,则补角的大小是( )
A. B. C. D.
11.(2022秋·广西梧州·七年级统考期末)关于补角有下列四个叙述:①锐角的补角是钝角;②只有锐角才有补角;③互为补角的两个角不可能相等;④同角或等角的补角一定相等. 其中正确的个数有( )
A.1 个 B.2个 C.3个 D.4个
12.(2022秋·广西桂林·七年级统考期末)下列说法:①所有直角都相等;②相等的角是直角;③同角的补角相等;④两点之间直线最短.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
13.(2022秋·广西崇左·七年级期末)如图所示,点A,O,B在同一直线上,∠COA=90°,若∠1=∠2,则图中互余的角共有( )
A.5对 B.4对 C.3对 D.2对
二、填空题
14.(2022秋·广西河池·七年级统考期末)如图,点C在点O的东北方向,点D在点O的北偏西方向,那么 .
15.(2022秋·广西梧州·七年级统考期末)从海岛A点观察海上两艘轮船B、C.轮船B在点A的北偏东60°方向;轮船C在点A的南偏西15°方向,则AB、AC组成的最小的角的度数是 度.
16.(2022秋·广西贺州·七年级统考期末) 度.
17.(2022秋·广西玉林·七年级统考期末) .
18.(2022秋·广西桂林·七年级统考期末)72.125°= 度 分 秒.
19.(2022秋·广西河池·七年级统考期末)一副三角板摆放在一起的示意图如下,若,则∠2的度数是 .
20.(2022秋·广西崇左·七年级期末)如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°41′,∠2的大小是 .
21.(2022秋·广西贺州·七年级统考期末)175°16′20″-45°30′÷6= .
22.(2022秋·广西钦州·七年级统考期末)计算:的结果为 .
23.(2022秋·广西百色·七年级统考期末)北京时间21点30分,此时钟表的时针和分针构成的角度是 .
24.(2022秋·广西百色·七年级统考期末)已知锐角,则的余角为 .
25.(2022秋·广西百色·七年级统考期末)已知 ∠AOB=∠COD=90°,则∠1 ∠2.(填“>,<,=”)
三、解答题
26.(2022秋·广西河池·七年级统考期末)如图,,,,平分.求的度数.
27.(2022秋·广西钦州·七年级统考期末)【探究】:哪些特殊的角可以用一副三角板画出?
(1)在①,②,③,④中,小明同学利用一副三角板画不出来的特殊角是________.
在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种,如图1,他先用三角板画出了直线,然后将一副三角板拼接在一起,其中角()的顶点与角()的顶点互相重合,且边,都在直线上.固定三角板不动,将三角板绕点按顺时针方向旋转一个角度,当边与射线第一次重合时停止.
(2)当平分时,求旋转角度.
(3)是否存在?若存在,求旋转角度;若不存在,请说明理由.
28.(2022秋·广西贵港·七年级统考期末)已知分别是和的平分线.
(1)如图1,如果重合,且在的内部,则 度;
(2)如图2,固定,将图1中的绕点O顺时针旋转().与旋转度数有怎样的数量关系?说明理由;
(3)如果的位置和大小不变,的边的位置不变,改变的大小;将图1中的绕着O点顺时针旋转(),如图3,请直接写出与旋转度数之间的数量关系: .
29.(2022秋·广西柳州·七年级统考期末)如图,已知为直线上一点,过点向直线上方引三条射线、、,且平分,,,求的度数.
30.(2022秋·广西梧州·七年级统考期末)如图,为直角,为锐角,且平分,平分.
(1)如果,求的度数.
(2)如果=,求的补角度数.
31.(2022秋·广西崇左·七年级统考期末)若一个角的余角是它的补角的,求这个角的度数.
32.(2022秋·广西桂林·七年级统考期末)如图,点A,O,B在一条直线上,,OD是的平分线.
(1)求和的度数.
(2)请直接写出图中的余角和补角.
参考答案:
1.C
【分析】按一定的规律数角的个数即可.
【详解】解:以OA 为一边的角有:,
以OD为一边的角有:,
以OC为一边的角有:,
所以,图中共有6个角,
故选:C.
【点睛】本题通过数角的个数,巩固角的概念,难度适中.
2.B
【分析】利用角度的三种表示方法,逐个进行分析即可.
【详解】解:A、图中表示的是不同的角,不能表示图中的角,不符合题意;
B、图中表示的是同一个角,符合题意;
C、图中表示的是同一个角,不能表示图中的角,不符合题意;
D、图中表示的是同一个角,表示的是另一个角,不符合题意;
故选B.
【点睛】本题考查了角的表示方法的应用,角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.
3.B
【分析】此时时针超过8点,分针指向4,根据每2个数字之间相隔30度和时针1分钟走0.5度可得夹角度数.
【详解】解:时针超过20分所走的度数为20×0.5=10°,
分针与8点之间的夹角为4×30=120°,
∴此时时钟面上的时针与分针的夹角是120+10=130°.
故选:B.
【点睛】本题考查钟面角的计算,用到的知识点为:钟面上每2个数字之间相隔30度;时针1分钟走0.5度.
4.C
【分析】根据一枚指针原来指向南偏西50°,逆时针旋转90°,可得答案.
【详解】解:指针原来指向南偏西50°,把这枚指针按逆时针方向旋转周,
即:南偏东40°,
故选:C.
【点睛】解答此类题需要从运动的角度,正确画出方位角,再结合角的和差关系求解.
5.D
【分析】根据方位角的概念,画图正确表示出方位角,即可求解.
【详解】解:由题意可知∠1=30°,
∵AP∥BQ,
∴∠1=∠2,由方向角的概念可知点Q看点P的方向是南偏西30°.
故选:D.
【点睛】本题考查了方向角的知识,属于基础题,解答此类题需要从运动的角度,正确画出方位角,找准中心是解答这类题的关键.
6.B
【分析】求出各个选项的角的度数,再判断即可.
【详解】解:A. 平角=90°,不符合题意;
B. 周角=72°,符合题意;
C. 直角=135°,不符合题意;
D. 周角=180°,不符合题意;
故选:B.
【点睛】本题考查了角的度量,解题关键是明确周角、平角、直角的度数.
7.D
【分析】∠ABC等于30度角与直角的和,据此即可计算得到.
【详解】解:∠ABC=30°+90°=120°.
故选:D.
【点睛】本题考查了角度的计算,理解三角板的角的度数是关键.
8.B
【分析】根据四边形的内角和等于及角平分线的定义即可求解.
【详解】解:∵,
∴,
又∵平分,平分,
∴,,
,
∴,
,
故选:B.
【点睛】本题考查了角平分线的有关计算,熟练掌握角平分线的定义是解题的关键.
9.D
【分析】根据互余两个角的数量关系,即可得到答案.
【详解】一个角的度数是,则这个角的余角是,
故选:.
【点睛】本题考查的是余角,熟练掌握定义是解题的关键.
10.D
【分析】根据补角的定义解答即可.
【详解】解:∵∠A=56°20′,
∴∠A的补角=180° ∠A=180° 56°20′=123°40′.
故选:D.
【点睛】本题主要考查了补角的定义以及角的度分秒换算,正确理解补角的定义是解题的关键.
11.B
【分析】根据和为180°的两个角互为补角即可判断①②③,根据等角或同角的补角相等即可判断④
【详解】解:锐角的补角是钝角,故①正确;
和为180°的两个角互为补角,故②不正确;
两个90°的角互为补角,且相等,故③不正确;
同角或等角的补角一定相等,故④正确
故正确的有①④,共2个
故选B
【点睛】本题考查了补角的定义,掌握补角的定义是解题的关键.
12.B
【分析】根据直角的定义,补角的定义以及两点之间线段最短,逐个分析个选项即可得出结果.
【详解】解:①直角都是90°,故所有的直角都相等,故①正确,
②相等的角不一定是直角,还有可能是对顶角,故②错误,
③两个角的和为180°的角互为补角,故同角的补角相等,故③正确,
④两点之间线段最短,故④错误,
所以①③两个正确.
故选:B.
【点睛】本题考查了直角的定义,补角的定义以及两点之间线段最短,需仔细分析每个选项,难度适中.
13.B
【分析】由∠AOC=90°,可求∠BOC=90°,推出∠1+∠AOE=90°,∠2+∠DOC=90°,求出∠DOC=∠AOE,推出∠1+∠COD=90°,∠2+∠AOE=90°,根据余角的定义得出即可.
【详解】解∵∠COA=90°∠AOC+∠BOC=180°
∴∠BOC=180°-90°=90°
∴∠AOC=∠BOC=90°,
∴∠1+∠AOE=90°,∠2+∠COD=90°.
∵∠1=∠2,
∴∠COD=∠AOE,
∴∠1+∠COD=90°,∠2+∠AOE=90°,
∴图中互余的角共有4对.
故选B.
【点睛】本题考查了邻补角,互余的应用,关键是熟悉:如果∠A和∠B互余,则∠A+∠B=90°.
14.
【分析】按照题目中已知的方位角,求和即可得到答案.
【详解】解:∵点C在点O的东北方向,点D在点O的北偏西方向,
∴,
故答案为:.
【点睛】此题考查了方位角,熟练掌握方位角的表示方法是是解题的关键.
15.135
【分析】首先根据题意画出草图,然后由方向角的定义,确定AB、AC与正北方向、正南方向的夹角;然后根据角的关系计算,即可求出∠BAC的度数.
【详解】解:如图,
∵轮船B在点A的北偏东60°方向;轮船C在点A的南偏西15°方向,
∴AB、AC组成的最小的角的度数∠BAC=15°+90°+90°-60°=135°.
故答案为:135.
【点睛】本题主要考查了方向角的知识,解决本题的关键是掌握方向角的定义.
16.
【分析】进行度、分、秒的转化运算,注意以60为进制,将度的小数部分化为分,将分的小数部分化为秒.
【详解】解:,,
度.
故答案为:.
【点睛】本题考查度分秒换算,由度化分应乘以60,由分化度应除以60,解题关键是注意度、分、秒都是60进制的,由小单位化大单位要除60即可.
17.
【分析】根据角度换算进制是,类比正常的实数运算进行即可得出结论.
【详解】解:
,
故答案为:.
【点睛】本题考查角度的运算,类比实数运算操作,掌握角度运算的换算进制是六十进制:是解决问题的关键.
18. 72 7 30
【分析】根据,进行转化即可.
【详解】解:∵,
∴72.125°=72度7分30秒
故答案为:72,7,30.
【点睛】本题考查了角的转化.解题的关键在于正确的计算.
19.35°/35度
【分析】根据图形直接用平角减去一个直角及∠1即可得出结果.
【详解】解:根据图形可得:
∠2=180°-90°-∠1=35°,
故答案为:35°.
【点睛】题目主要考查简单的三角板中的角度计算,结合图形进行求解是解题关键.
20.57°41′
【分析】先利用∠1求出∠EAC的度数,再利用90°减去∠EAC即可解答.
【详解】解:∵∠BAC=60°,∠1=27°41′,
∴∠EAC=∠BAC ∠1=60° 27°41′=32°19′,
∵∠EAD=90°,
∴∠2=∠EAD ∠EAC=90° 32°19′=57°41′,
故答案为:57°41′.
【点睛】本题考查了度分秒的换算,熟练掌握度分秒的进制是解题的关键.
21.167°41′20″
【分析】先计算除法,再计算减法运算,注意要根据度分秒的进制进行计算.
【详解】解:175°16′20″-45°30′÷6
=175°16′20″-42°210′÷6
=175°16′20″-7°35′
=174°76′20″-7°35′
=167°41′20″,
故答案为:167°41′20″.
【点睛】本题考查了度分秒的换算,熟练掌握度分秒的进制是解题的关键.
22.
【分析】根据角的运算法则进行计算即可得到结果.
【详解】解:,
故答案为:.
【点睛】此题主要考查了角的运算,解题的关键是注意:,.
23.105
【分析】根据题意,得3、9点所在直线和6、12点所在直线垂直,通过角度的乘除和和差运算,即可得到答案.
【详解】如图
∵3、9点所在直线和6、12点所在直线垂直
∴北京时间21点30分时,分针和x的夹角为:
∴此时钟表的时针和分针构成的角度是:
故答案为:105.
【点睛】本题考查了角的知识;解题的关键是熟练掌握角度的乘除和和差计算,即可得到答案.
24./
【分析】根据余角的概念进行计算即可.
【详解】或
故答案为:或
【点睛】本题考查了余角的定义,即和为90度的两个角,还涉及角的和差,熟练掌握知识点是解题的关键.
25.=
【分析】根据等角的余角相等即可求解.
【详解】解:;∠AOB=∠COD=90°
故答案为:=
【点睛】此题考查角的计算,掌握等角的余角相等是解题的关键.
26.
【分析】根据已知得出根据角平分线的定义得出即根据即可求解.
【详解】解:
∴
∵平分,
∴
∴
∴
【点睛】本题考查了角平分线的定义,几何图形中角度的计算,数形结合是解题的关键.
27.(1)④
(2)
(3)或
【分析】(1)根据一副三角板中的特殊角,运用角的和与差的计算,只要是15°的倍数的角都可以画出来;
(2)根据已知条件得到,根据角平分线的定义得到,于是得到结论;
(3)当在的左侧时,当在的右侧时,列方程即可得到结论.
【详解】(1)解:∵,,,
∴不能写成的和或差,故画不出;
故答案为:④;
(2)解:∵,
∴,
∵平分,
∴,
∵,
∴;
(3)当OA在OD的左侧时,如图 ①,
则,,
∵,
∴,
∴;
当在的右侧时如图②,则,,
∵,
∴,
∴,
综上所述,当或时,存在.
【点睛】本题考查了解得计算,特殊角,角平分线的定义,正确的理解题意是解题的关键.
28.(1)25°
(2),见解析
(3)
【分析】(1)利用角平分线的定义可求得的度数,结论可得;
(2)利用(1)中的方法计算的度数,利用旋转度数表示;
(3)利用角平分线的定义可求得的度数,再利用角的和差得出结论.
【详解】(1)解:如图1,∵平分,
∴,
∵平分,
∴,
∴;
(2)解:如图2,;
(3)解:如图3中,当在内部时,
,
当在外部时,
,
综上所述,.
故答案为:.
【点睛】本题考查了角平分线的定义,邻补角定义,角的和差关系,掌握角的和差关系,分类讨论是关键.
29.
【分析】设,则,根据题意的,根据角平分线的定义可得,根据,建立方程,解方程即可求解.
【详解】解:设,则,
∵,
∴
∵平分,
∴,
∵,
∴
解得:,
∴,
答:的度数为
【点睛】本题考查了几何图形中角度的计算,平角的定义,角平分线的定义,一元一次方程的应用,数形结合是解题的关键.
30.(1)45°
(2)135°
【分析】(1)根据∠AOB=90°,∠AOC=50° ,可得∠BOC=140° ,再由平分,平分,可得∠MOC=70°,∠NOC=25°,即可求解;
(2)根据=,可得∠BOC=90°+,再由平分,平分,可得,即可求解.
【详解】(1)解:∵∠AOB=90°,∠AOC=50° ,
∴∠BOC=∠AOB+∠AOC=90°+50°=140° ,
又∵OM平分∠BOC,ON平分∠AOC ,
∴∠MOC=70°,∠NOC=25°,
∴∠MON=∠MOC-∠NOC=70°-25°=45°,
(2)解:∵=,
∴∠BOC=∠AOB+∠AOC=90°+,
∵OM平分∠BOC,ON平分∠AOC,
∴
∴的补角为:.
【点睛】本题主要考查了有关角平分线的计算,求一个角的补角,明确题意,准确得到角与角之间的数量关系是解题的关键.
31.这个角的度数是
【分析】首先根据余角与补角的定义,设这个角为,则它的余角为,补角为,再根据题中给出的等量关系列方程即可求解.
【详解】解:设这个角为,
由题意,得,
解得:,
所以这个角的度数是.
【点睛】此题综合考查余角与补角,解题的关键是掌握一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式和方程求解.
32.(1),
(2)的余角为和, 的补角为
【分析】(1)根据∠AOE=∠AOC+∠COE代入数据进行计算即可得解;根据角平分线的定义可得∠COD=∠AOC,然后根据∠DOE=∠COD+∠COE代入数据进行计算即可得解;
(2)根据∠COD的度数确定其余角和补角.
【详解】(1)解:∵,,
∴.
∵OD是的平分线,
∴,
∴.
(2)解:的余角为和;
的补角为.
【点睛】本题考查了余角和补角,角平分线的定义,熟记概念并准确识图,确定出图中各角度之间的关系是解题的关键.
一、单选题
1.(2022秋·广西贺州·七年级统考期末)如图,从的顶点引出两条射线OC,OD,图中的角共有( )
A.3个 B.4个 C.6个 D.7个
2.(2022秋·广西河池·七年级统考期末)下列四个图中,能用三种方法表示同一个角的是( )
A. B.
C. D.
3.(2022秋·广西崇左·七年级统考期末)如图,从8点钟开始,过了20分钟后,分针与时针所夹的度数是( )
A. B. C. D.
4.(2022秋·广西防城港·七年级统考期末)某测绘装置上一枚指针原来指向南偏西50°(如图),把这枚指针按逆时针方向旋转周,则结果指针的指向( )
A.南偏东50° B.西偏北50° C.南偏东40° D.东南方向
5.(2022秋·广西柳州·七年级统考期末)点看点的方向是北偏东,那么点看点的方向是( )
A.南偏东 B.南偏西 C.南偏东 D.南偏西
6.(2022秋·广西桂林·七年级统考期末)下列各角中,为锐角的是( )
A.平角 B.周角 C.直角 D.周角
7.(2022秋·广西钦州·七年级统考期末)把两块三角板按如图所示那样拼在一起,则∠ABC等于( )
A.70° B.90° C.105° D.120°
8.(2022春·广西玉林·七年级统考期末)如图,已知//,平分,平分.若,则的度数为( )(注:四边形内角和等于)
A. B. C. D.
9.(2022秋·广西贺州·七年级统考期末)一个角的度数是,则这个角的余角是( )
A. B. C. D.
10.(2022秋·广西崇左·七年级统考期末)若,则补角的大小是( )
A. B. C. D.
11.(2022秋·广西梧州·七年级统考期末)关于补角有下列四个叙述:①锐角的补角是钝角;②只有锐角才有补角;③互为补角的两个角不可能相等;④同角或等角的补角一定相等. 其中正确的个数有( )
A.1 个 B.2个 C.3个 D.4个
12.(2022秋·广西桂林·七年级统考期末)下列说法:①所有直角都相等;②相等的角是直角;③同角的补角相等;④两点之间直线最短.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
13.(2022秋·广西崇左·七年级期末)如图所示,点A,O,B在同一直线上,∠COA=90°,若∠1=∠2,则图中互余的角共有( )
A.5对 B.4对 C.3对 D.2对
二、填空题
14.(2022秋·广西河池·七年级统考期末)如图,点C在点O的东北方向,点D在点O的北偏西方向,那么 .
15.(2022秋·广西梧州·七年级统考期末)从海岛A点观察海上两艘轮船B、C.轮船B在点A的北偏东60°方向;轮船C在点A的南偏西15°方向,则AB、AC组成的最小的角的度数是 度.
16.(2022秋·广西贺州·七年级统考期末) 度.
17.(2022秋·广西玉林·七年级统考期末) .
18.(2022秋·广西桂林·七年级统考期末)72.125°= 度 分 秒.
19.(2022秋·广西河池·七年级统考期末)一副三角板摆放在一起的示意图如下,若,则∠2的度数是 .
20.(2022秋·广西崇左·七年级期末)如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°41′,∠2的大小是 .
21.(2022秋·广西贺州·七年级统考期末)175°16′20″-45°30′÷6= .
22.(2022秋·广西钦州·七年级统考期末)计算:的结果为 .
23.(2022秋·广西百色·七年级统考期末)北京时间21点30分,此时钟表的时针和分针构成的角度是 .
24.(2022秋·广西百色·七年级统考期末)已知锐角,则的余角为 .
25.(2022秋·广西百色·七年级统考期末)已知 ∠AOB=∠COD=90°,则∠1 ∠2.(填“>,<,=”)
三、解答题
26.(2022秋·广西河池·七年级统考期末)如图,,,,平分.求的度数.
27.(2022秋·广西钦州·七年级统考期末)【探究】:哪些特殊的角可以用一副三角板画出?
(1)在①,②,③,④中,小明同学利用一副三角板画不出来的特殊角是________.
在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种,如图1,他先用三角板画出了直线,然后将一副三角板拼接在一起,其中角()的顶点与角()的顶点互相重合,且边,都在直线上.固定三角板不动,将三角板绕点按顺时针方向旋转一个角度,当边与射线第一次重合时停止.
(2)当平分时,求旋转角度.
(3)是否存在?若存在,求旋转角度;若不存在,请说明理由.
28.(2022秋·广西贵港·七年级统考期末)已知分别是和的平分线.
(1)如图1,如果重合,且在的内部,则 度;
(2)如图2,固定,将图1中的绕点O顺时针旋转().与旋转度数有怎样的数量关系?说明理由;
(3)如果的位置和大小不变,的边的位置不变,改变的大小;将图1中的绕着O点顺时针旋转(),如图3,请直接写出与旋转度数之间的数量关系: .
29.(2022秋·广西柳州·七年级统考期末)如图,已知为直线上一点,过点向直线上方引三条射线、、,且平分,,,求的度数.
30.(2022秋·广西梧州·七年级统考期末)如图,为直角,为锐角,且平分,平分.
(1)如果,求的度数.
(2)如果=,求的补角度数.
31.(2022秋·广西崇左·七年级统考期末)若一个角的余角是它的补角的,求这个角的度数.
32.(2022秋·广西桂林·七年级统考期末)如图,点A,O,B在一条直线上,,OD是的平分线.
(1)求和的度数.
(2)请直接写出图中的余角和补角.
参考答案:
1.C
【分析】按一定的规律数角的个数即可.
【详解】解:以OA 为一边的角有:,
以OD为一边的角有:,
以OC为一边的角有:,
所以,图中共有6个角,
故选:C.
【点睛】本题通过数角的个数,巩固角的概念,难度适中.
2.B
【分析】利用角度的三种表示方法,逐个进行分析即可.
【详解】解:A、图中表示的是不同的角,不能表示图中的角,不符合题意;
B、图中表示的是同一个角,符合题意;
C、图中表示的是同一个角,不能表示图中的角,不符合题意;
D、图中表示的是同一个角,表示的是另一个角,不符合题意;
故选B.
【点睛】本题考查了角的表示方法的应用,角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.
3.B
【分析】此时时针超过8点,分针指向4,根据每2个数字之间相隔30度和时针1分钟走0.5度可得夹角度数.
【详解】解:时针超过20分所走的度数为20×0.5=10°,
分针与8点之间的夹角为4×30=120°,
∴此时时钟面上的时针与分针的夹角是120+10=130°.
故选:B.
【点睛】本题考查钟面角的计算,用到的知识点为:钟面上每2个数字之间相隔30度;时针1分钟走0.5度.
4.C
【分析】根据一枚指针原来指向南偏西50°,逆时针旋转90°,可得答案.
【详解】解:指针原来指向南偏西50°,把这枚指针按逆时针方向旋转周,
即:南偏东40°,
故选:C.
【点睛】解答此类题需要从运动的角度,正确画出方位角,再结合角的和差关系求解.
5.D
【分析】根据方位角的概念,画图正确表示出方位角,即可求解.
【详解】解:由题意可知∠1=30°,
∵AP∥BQ,
∴∠1=∠2,由方向角的概念可知点Q看点P的方向是南偏西30°.
故选:D.
【点睛】本题考查了方向角的知识,属于基础题,解答此类题需要从运动的角度,正确画出方位角,找准中心是解答这类题的关键.
6.B
【分析】求出各个选项的角的度数,再判断即可.
【详解】解:A. 平角=90°,不符合题意;
B. 周角=72°,符合题意;
C. 直角=135°,不符合题意;
D. 周角=180°,不符合题意;
故选:B.
【点睛】本题考查了角的度量,解题关键是明确周角、平角、直角的度数.
7.D
【分析】∠ABC等于30度角与直角的和,据此即可计算得到.
【详解】解:∠ABC=30°+90°=120°.
故选:D.
【点睛】本题考查了角度的计算,理解三角板的角的度数是关键.
8.B
【分析】根据四边形的内角和等于及角平分线的定义即可求解.
【详解】解:∵,
∴,
又∵平分,平分,
∴,,
,
∴,
,
故选:B.
【点睛】本题考查了角平分线的有关计算,熟练掌握角平分线的定义是解题的关键.
9.D
【分析】根据互余两个角的数量关系,即可得到答案.
【详解】一个角的度数是,则这个角的余角是,
故选:.
【点睛】本题考查的是余角,熟练掌握定义是解题的关键.
10.D
【分析】根据补角的定义解答即可.
【详解】解:∵∠A=56°20′,
∴∠A的补角=180° ∠A=180° 56°20′=123°40′.
故选:D.
【点睛】本题主要考查了补角的定义以及角的度分秒换算,正确理解补角的定义是解题的关键.
11.B
【分析】根据和为180°的两个角互为补角即可判断①②③,根据等角或同角的补角相等即可判断④
【详解】解:锐角的补角是钝角,故①正确;
和为180°的两个角互为补角,故②不正确;
两个90°的角互为补角,且相等,故③不正确;
同角或等角的补角一定相等,故④正确
故正确的有①④,共2个
故选B
【点睛】本题考查了补角的定义,掌握补角的定义是解题的关键.
12.B
【分析】根据直角的定义,补角的定义以及两点之间线段最短,逐个分析个选项即可得出结果.
【详解】解:①直角都是90°,故所有的直角都相等,故①正确,
②相等的角不一定是直角,还有可能是对顶角,故②错误,
③两个角的和为180°的角互为补角,故同角的补角相等,故③正确,
④两点之间线段最短,故④错误,
所以①③两个正确.
故选:B.
【点睛】本题考查了直角的定义,补角的定义以及两点之间线段最短,需仔细分析每个选项,难度适中.
13.B
【分析】由∠AOC=90°,可求∠BOC=90°,推出∠1+∠AOE=90°,∠2+∠DOC=90°,求出∠DOC=∠AOE,推出∠1+∠COD=90°,∠2+∠AOE=90°,根据余角的定义得出即可.
【详解】解∵∠COA=90°∠AOC+∠BOC=180°
∴∠BOC=180°-90°=90°
∴∠AOC=∠BOC=90°,
∴∠1+∠AOE=90°,∠2+∠COD=90°.
∵∠1=∠2,
∴∠COD=∠AOE,
∴∠1+∠COD=90°,∠2+∠AOE=90°,
∴图中互余的角共有4对.
故选B.
【点睛】本题考查了邻补角,互余的应用,关键是熟悉:如果∠A和∠B互余,则∠A+∠B=90°.
14.
【分析】按照题目中已知的方位角,求和即可得到答案.
【详解】解:∵点C在点O的东北方向,点D在点O的北偏西方向,
∴,
故答案为:.
【点睛】此题考查了方位角,熟练掌握方位角的表示方法是是解题的关键.
15.135
【分析】首先根据题意画出草图,然后由方向角的定义,确定AB、AC与正北方向、正南方向的夹角;然后根据角的关系计算,即可求出∠BAC的度数.
【详解】解:如图,
∵轮船B在点A的北偏东60°方向;轮船C在点A的南偏西15°方向,
∴AB、AC组成的最小的角的度数∠BAC=15°+90°+90°-60°=135°.
故答案为:135.
【点睛】本题主要考查了方向角的知识,解决本题的关键是掌握方向角的定义.
16.
【分析】进行度、分、秒的转化运算,注意以60为进制,将度的小数部分化为分,将分的小数部分化为秒.
【详解】解:,,
度.
故答案为:.
【点睛】本题考查度分秒换算,由度化分应乘以60,由分化度应除以60,解题关键是注意度、分、秒都是60进制的,由小单位化大单位要除60即可.
17.
【分析】根据角度换算进制是,类比正常的实数运算进行即可得出结论.
【详解】解:
,
故答案为:.
【点睛】本题考查角度的运算,类比实数运算操作,掌握角度运算的换算进制是六十进制:是解决问题的关键.
18. 72 7 30
【分析】根据,进行转化即可.
【详解】解:∵,
∴72.125°=72度7分30秒
故答案为:72,7,30.
【点睛】本题考查了角的转化.解题的关键在于正确的计算.
19.35°/35度
【分析】根据图形直接用平角减去一个直角及∠1即可得出结果.
【详解】解:根据图形可得:
∠2=180°-90°-∠1=35°,
故答案为:35°.
【点睛】题目主要考查简单的三角板中的角度计算,结合图形进行求解是解题关键.
20.57°41′
【分析】先利用∠1求出∠EAC的度数,再利用90°减去∠EAC即可解答.
【详解】解:∵∠BAC=60°,∠1=27°41′,
∴∠EAC=∠BAC ∠1=60° 27°41′=32°19′,
∵∠EAD=90°,
∴∠2=∠EAD ∠EAC=90° 32°19′=57°41′,
故答案为:57°41′.
【点睛】本题考查了度分秒的换算,熟练掌握度分秒的进制是解题的关键.
21.167°41′20″
【分析】先计算除法,再计算减法运算,注意要根据度分秒的进制进行计算.
【详解】解:175°16′20″-45°30′÷6
=175°16′20″-42°210′÷6
=175°16′20″-7°35′
=174°76′20″-7°35′
=167°41′20″,
故答案为:167°41′20″.
【点睛】本题考查了度分秒的换算,熟练掌握度分秒的进制是解题的关键.
22.
【分析】根据角的运算法则进行计算即可得到结果.
【详解】解:,
故答案为:.
【点睛】此题主要考查了角的运算,解题的关键是注意:,.
23.105
【分析】根据题意,得3、9点所在直线和6、12点所在直线垂直,通过角度的乘除和和差运算,即可得到答案.
【详解】如图
∵3、9点所在直线和6、12点所在直线垂直
∴北京时间21点30分时,分针和x的夹角为:
∴此时钟表的时针和分针构成的角度是:
故答案为:105.
【点睛】本题考查了角的知识;解题的关键是熟练掌握角度的乘除和和差计算,即可得到答案.
24./
【分析】根据余角的概念进行计算即可.
【详解】或
故答案为:或
【点睛】本题考查了余角的定义,即和为90度的两个角,还涉及角的和差,熟练掌握知识点是解题的关键.
25.=
【分析】根据等角的余角相等即可求解.
【详解】解:;∠AOB=∠COD=90°
故答案为:=
【点睛】此题考查角的计算,掌握等角的余角相等是解题的关键.
26.
【分析】根据已知得出根据角平分线的定义得出即根据即可求解.
【详解】解:
∴
∵平分,
∴
∴
∴
【点睛】本题考查了角平分线的定义,几何图形中角度的计算,数形结合是解题的关键.
27.(1)④
(2)
(3)或
【分析】(1)根据一副三角板中的特殊角,运用角的和与差的计算,只要是15°的倍数的角都可以画出来;
(2)根据已知条件得到,根据角平分线的定义得到,于是得到结论;
(3)当在的左侧时,当在的右侧时,列方程即可得到结论.
【详解】(1)解:∵,,,
∴不能写成的和或差,故画不出;
故答案为:④;
(2)解:∵,
∴,
∵平分,
∴,
∵,
∴;
(3)当OA在OD的左侧时,如图 ①,
则,,
∵,
∴,
∴;
当在的右侧时如图②,则,,
∵,
∴,
∴,
综上所述,当或时,存在.
【点睛】本题考查了解得计算,特殊角,角平分线的定义,正确的理解题意是解题的关键.
28.(1)25°
(2),见解析
(3)
【分析】(1)利用角平分线的定义可求得的度数,结论可得;
(2)利用(1)中的方法计算的度数,利用旋转度数表示;
(3)利用角平分线的定义可求得的度数,再利用角的和差得出结论.
【详解】(1)解:如图1,∵平分,
∴,
∵平分,
∴,
∴;
(2)解:如图2,;
(3)解:如图3中,当在内部时,
,
当在外部时,
,
综上所述,.
故答案为:.
【点睛】本题考查了角平分线的定义,邻补角定义,角的和差关系,掌握角的和差关系,分类讨论是关键.
29.
【分析】设,则,根据题意的,根据角平分线的定义可得,根据,建立方程,解方程即可求解.
【详解】解:设,则,
∵,
∴
∵平分,
∴,
∵,
∴
解得:,
∴,
答:的度数为
【点睛】本题考查了几何图形中角度的计算,平角的定义,角平分线的定义,一元一次方程的应用,数形结合是解题的关键.
30.(1)45°
(2)135°
【分析】(1)根据∠AOB=90°,∠AOC=50° ,可得∠BOC=140° ,再由平分,平分,可得∠MOC=70°,∠NOC=25°,即可求解;
(2)根据=,可得∠BOC=90°+,再由平分,平分,可得,即可求解.
【详解】(1)解:∵∠AOB=90°,∠AOC=50° ,
∴∠BOC=∠AOB+∠AOC=90°+50°=140° ,
又∵OM平分∠BOC,ON平分∠AOC ,
∴∠MOC=70°,∠NOC=25°,
∴∠MON=∠MOC-∠NOC=70°-25°=45°,
(2)解:∵=,
∴∠BOC=∠AOB+∠AOC=90°+,
∵OM平分∠BOC,ON平分∠AOC,
∴
∴的补角为:.
【点睛】本题主要考查了有关角平分线的计算,求一个角的补角,明确题意,准确得到角与角之间的数量关系是解题的关键.
31.这个角的度数是
【分析】首先根据余角与补角的定义,设这个角为,则它的余角为,补角为,再根据题中给出的等量关系列方程即可求解.
【详解】解:设这个角为,
由题意,得,
解得:,
所以这个角的度数是.
【点睛】此题综合考查余角与补角,解题的关键是掌握一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式和方程求解.
32.(1),
(2)的余角为和, 的补角为
【分析】(1)根据∠AOE=∠AOC+∠COE代入数据进行计算即可得解;根据角平分线的定义可得∠COD=∠AOC,然后根据∠DOE=∠COD+∠COE代入数据进行计算即可得解;
(2)根据∠COD的度数确定其余角和补角.
【详解】(1)解:∵,,
∴.
∵OD是的平分线,
∴,
∴.
(2)解:的余角为和;
的补角为.
【点睛】本题考查了余角和补角,角平分线的定义,熟记概念并准确识图,确定出图中各角度之间的关系是解题的关键.
