2.2 轴对称的性质 练习题 (无答案)2023-2024学年苏科版八年级数学上册
文档属性
| 名称 | 2.2 轴对称的性质 练习题 (无答案)2023-2024学年苏科版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 13:19:40 | ||
图片预览

文档简介
2.2 轴对称的性质
一.选择题
1.一条两边沿互相平行的围巾按图所示折叠,已知∠DAB﹣∠ABC=8°,且DF∥CG,则∠DAB+2∠ABC=( )度.
A.130 B.131 C.132 D.133
2.如图,在△ABC中,点D是AC边上的中点,连接BD,把△ABD沿着BD翻折,得到△A'BD,连接A'C,若A′C=6,∠A'CD=30°,BD=4,则点A'到直线AB的距离为( )
A. B.2 C. D.3
3.如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠1=115°,则图中∠2的度数为( )
A.40° B.45° C.50° D.60°
4.如图,在三角形纸片ABC中,∠ACB=90°,BC=5,AB=13,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,点A与BC延长线上的点D重合,CE的长( )
A. B.3 C. D.
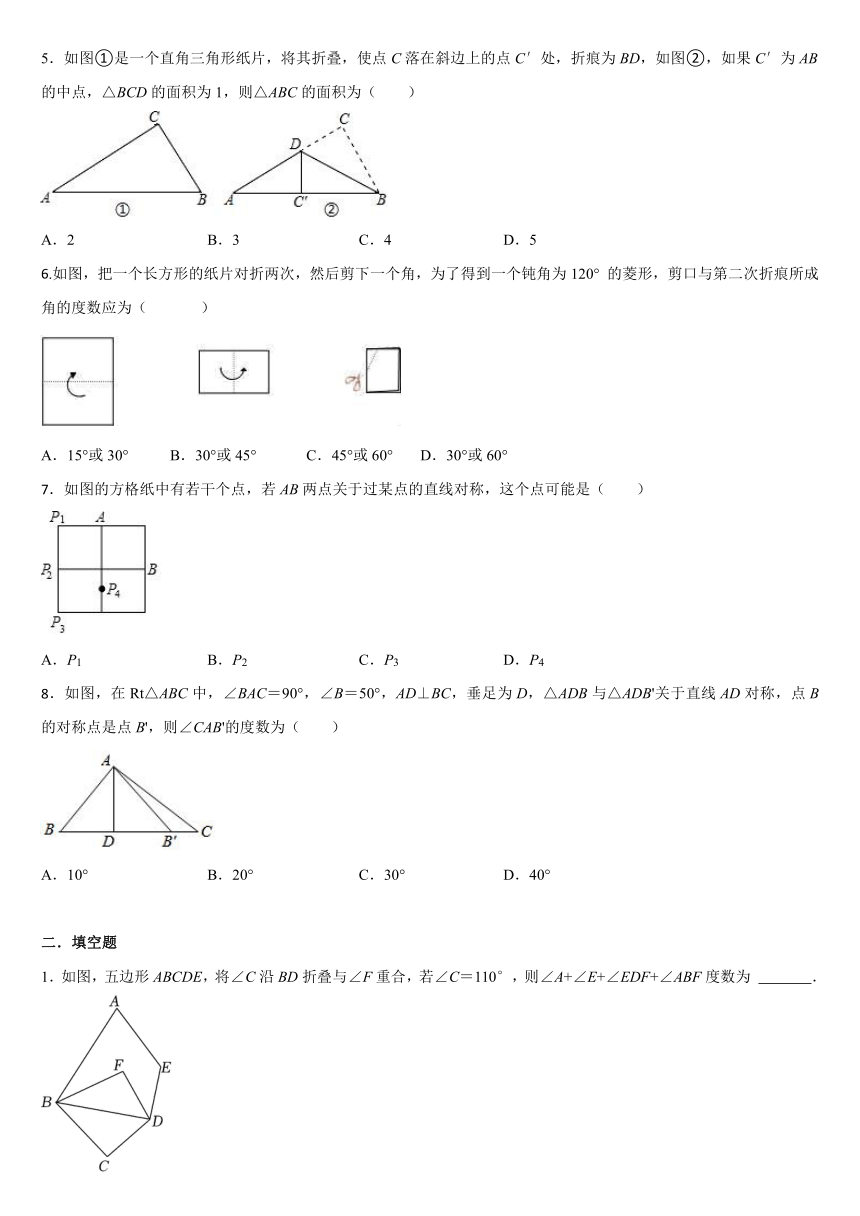
5.如图①是一个直角三角形纸片,将其折叠,使点C落在斜边上的点C′处,折痕为BD,如图②,如果C′为AB的中点,△BCD的面积为1,则△ABC的面积为( )
A.2 B.3 C.4 D.5
6.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120° 的菱形,剪口与第二次折痕所成角的度数应为( )
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
7.如图的方格纸中有若干个点,若AB两点关于过某点的直线对称,这个点可能是( )
A.P1 B.P2 C.P3 D.P4
8.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20° C.30° D.40°
二.填空题
1.如图,五边形ABCDE,将∠C沿BD折叠与∠F重合,若∠C=110°,则∠A+∠E+∠EDF+∠ABF度数为 .
2.如图,△ABC中,点D为边BC的中点,连接AD,将△ADC沿直线AD翻折至△ABC所在平面内,得△ADC′,连接CC′,分别与边AB交于点E,与AD交于点O.若AE=BE,AD=6,则BC′的长为 .
3.如图,在三角形纸片ABC中,点D,E,F分别在边AB,AC,BC上,BC=20,BF=12,将这张纸片沿直线DE翻折,点A与点F重合,若DE∥BC,AF=DF,则四边形ADFE的面积为 .
4.如图,四边形纸片ABCD中,∠C=∠D=90°,AD=3,BC=9,CD=8,点E在BC上,且AE⊥BC.将四边形纸片ABCD沿AE折叠,点C、D分别落在点C'、D'处,C'D'与AB交于点F,则BF长为 .
5.如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕到BC的距离记为h2;按上述方法不断操作下去…,经过第2022次操作后得到的折痕D2021E2021,到BC的距离记为h2022;若h1=1,则h2022的值为 .
三.解答题
1.如图,△ABC和△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若∠BAC=108°,∠BAE=30°,求∠EAF的度数.
2.如图,D为AB的中点,点E在AC上,将△ABC沿DE折叠,使点A落在BC边上的点F处.
求证:EF=EC.
3.认真观察图(1)的4个图中阴影部分构成的图案,回答下列问题:
(1)请写出这四个图案都具有的两个共同特征.
特征1:______________________________________________;
特征2:______________________________________________.
(2)请在图(2)中设计出你心中最美丽的图案,使它也具备你所写出的上述特征.
4.在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A(﹣3,﹣1).点B(﹣2,﹣4),点C(﹣1,﹣2).
(1)将△ABC先向右平移4个单位,再向上平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于x轴对称的△A2B2C2,并写出点B2的坐标.
一.选择题
1.一条两边沿互相平行的围巾按图所示折叠,已知∠DAB﹣∠ABC=8°,且DF∥CG,则∠DAB+2∠ABC=( )度.
A.130 B.131 C.132 D.133
2.如图,在△ABC中,点D是AC边上的中点,连接BD,把△ABD沿着BD翻折,得到△A'BD,连接A'C,若A′C=6,∠A'CD=30°,BD=4,则点A'到直线AB的距离为( )
A. B.2 C. D.3
3.如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠1=115°,则图中∠2的度数为( )
A.40° B.45° C.50° D.60°
4.如图,在三角形纸片ABC中,∠ACB=90°,BC=5,AB=13,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,点A与BC延长线上的点D重合,CE的长( )
A. B.3 C. D.
5.如图①是一个直角三角形纸片,将其折叠,使点C落在斜边上的点C′处,折痕为BD,如图②,如果C′为AB的中点,△BCD的面积为1,则△ABC的面积为( )
A.2 B.3 C.4 D.5
6.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120° 的菱形,剪口与第二次折痕所成角的度数应为( )
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
7.如图的方格纸中有若干个点,若AB两点关于过某点的直线对称,这个点可能是( )
A.P1 B.P2 C.P3 D.P4
8.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20° C.30° D.40°
二.填空题
1.如图,五边形ABCDE,将∠C沿BD折叠与∠F重合,若∠C=110°,则∠A+∠E+∠EDF+∠ABF度数为 .
2.如图,△ABC中,点D为边BC的中点,连接AD,将△ADC沿直线AD翻折至△ABC所在平面内,得△ADC′,连接CC′,分别与边AB交于点E,与AD交于点O.若AE=BE,AD=6,则BC′的长为 .
3.如图,在三角形纸片ABC中,点D,E,F分别在边AB,AC,BC上,BC=20,BF=12,将这张纸片沿直线DE翻折,点A与点F重合,若DE∥BC,AF=DF,则四边形ADFE的面积为 .
4.如图,四边形纸片ABCD中,∠C=∠D=90°,AD=3,BC=9,CD=8,点E在BC上,且AE⊥BC.将四边形纸片ABCD沿AE折叠,点C、D分别落在点C'、D'处,C'D'与AB交于点F,则BF长为 .
5.如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕到BC的距离记为h2;按上述方法不断操作下去…,经过第2022次操作后得到的折痕D2021E2021,到BC的距离记为h2022;若h1=1,则h2022的值为 .
三.解答题
1.如图,△ABC和△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若∠BAC=108°,∠BAE=30°,求∠EAF的度数.
2.如图,D为AB的中点,点E在AC上,将△ABC沿DE折叠,使点A落在BC边上的点F处.
求证:EF=EC.
3.认真观察图(1)的4个图中阴影部分构成的图案,回答下列问题:
(1)请写出这四个图案都具有的两个共同特征.
特征1:______________________________________________;
特征2:______________________________________________.
(2)请在图(2)中设计出你心中最美丽的图案,使它也具备你所写出的上述特征.
4.在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A(﹣3,﹣1).点B(﹣2,﹣4),点C(﹣1,﹣2).
(1)将△ABC先向右平移4个单位,再向上平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于x轴对称的△A2B2C2,并写出点B2的坐标.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
