11.1与三角形有关的线段 同步练习(含答案)2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 11.1与三角形有关的线段 同步练习(含答案)2023—2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 87.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 13:22:44 | ||
图片预览

文档简介
11.1与三角形有关的线段
一、选择题
1.下列选项中的三条线段能首尾相接构成三角形的是( )
A.1cm,2cm,4cm B.3cm,4cm,8cm
C.9cm,6cm,4cm D.5cm,5cm,10cm
2.空调安装在墙上时,一般都会采用如图所示的方法固定,这样做的道理是( )
A.两点之间连线最短 B.经过两点有且只有一条直线
C.三角形具有稳定性 D.垂线段最短
3.一个三角形的两条边分别为,,则它的第三边可能是( )
A. B. C. D.
4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B.
C. D.
5.四根长度分别为、、、的木条,以其中三根的长为边长,制作成一个三角形框架,那么这个框架的周长可能是( )
A. B. C. D.
6.能把一个三角形分成两个面积相等的三角形的是三角形的( )
A.角平分线 B.中线 C.高线 D.重心
7.如图,AD是△ABC的中线,△ABD比△ACD的周长大6 cm,则AB与AC的差为( )
A.2 cm B.3 cm C.6 cm D.12 cm
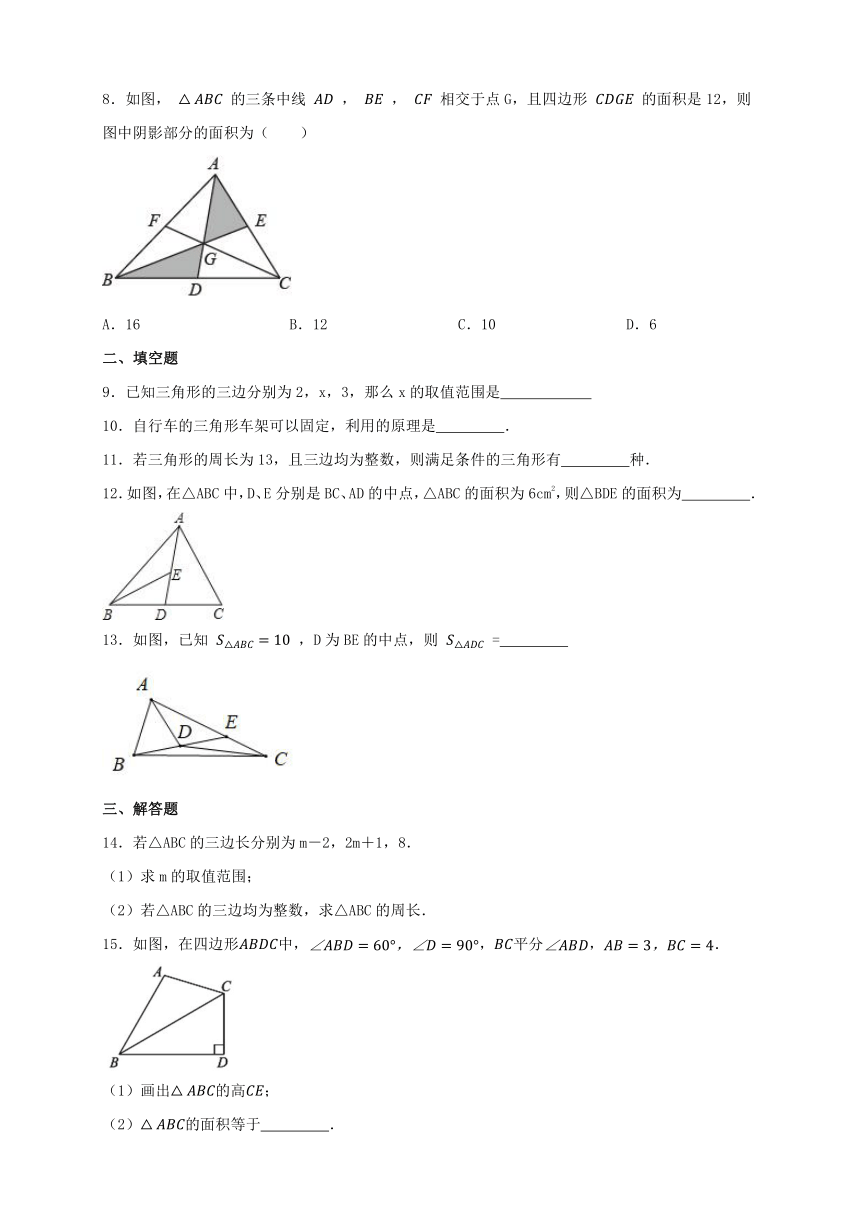
8.如图, 的三条中线 , , 相交于点G,且四边形 的面积是12,则图中阴影部分的面积为( )
A.16 B.12 C.10 D.6
二、填空题
9.已知三角形的三边分别为2,x,3,那么x的取值范围是
10.自行车的三角形车架可以固定,利用的原理是 .
11.若三角形的周长为13,且三边均为整数,则满足条件的三角形有 种.
12.如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2,则△BDE的面积为 .
13.如图,已知 ,D为BE的中点,则 =
三、解答题
14.若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
15.如图,在四边形中,,平分,.
(1)画出的高;
(2)的面积等于 .
16.如图,已知AD、AE分别是△ABC的高和中线,△ABE的面积为12cm2,AD=4.8cm,∠CAB=90°,AB=6cm.求:
(1)BC的长;
(2)△ABC的周长.
17.已知 △ABC 的周长为 37cm , AD 是 BC 边上的中线, .
(1)如图,当AB=15cm 时,求 BD 的长.
(2)若 ,能否求出 的长?为什么?
参考答案
1.C
2.C
3.B
4.A
5.C
6.B
7.C
8.B
9.1<x<5
10.稳定性
11.5
12.
13.5
14.(1)解:根据三角形的三边关系,
,
解得:3<m<5;
(2)解:因为△ABC的三边均为整数,且3<m<5,所以m=4.
所以,△ABC 的周长为:(m 2)+(2m+1)+8=3m+7=3×4+7=19.
15.(1)解:如图所示,高即为所求;
(2)3
16.(1)解:∵△ABE的面积为12cm2,AD是△ABC的高,AD=4.8cm,
∴=5cm,
∵AE是△ABC的中线,
∴BC=2BE=10cm;
(2)解:∵AD是△ABC的高,AD=4.8cm,BC=10cm,
∴△ABC的面积:=24cm2,
∵在△ABC中,∠CAB=90°,AB=6cm,
∴△ABC的面积:=24cm2
∴AC=8cm,
∴△ABC的周长:AC+BC+AB=24cm.
17.(1)解:∵ , ,
∴ ,
又∵ 的周长为 ,
∴ ,
∴ ,
又∵ 是 边上的中线,
∴ ;
(2)解:不能,理由如下:
∵ , ,
∴ ,
又∵ 的周长为 ,
∴ ,
∴ ,
∴BC+AC=16∴不能构成三角形,故不能求出DC的长.
一、选择题
1.下列选项中的三条线段能首尾相接构成三角形的是( )
A.1cm,2cm,4cm B.3cm,4cm,8cm
C.9cm,6cm,4cm D.5cm,5cm,10cm
2.空调安装在墙上时,一般都会采用如图所示的方法固定,这样做的道理是( )
A.两点之间连线最短 B.经过两点有且只有一条直线
C.三角形具有稳定性 D.垂线段最短
3.一个三角形的两条边分别为,,则它的第三边可能是( )
A. B. C. D.
4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B.
C. D.
5.四根长度分别为、、、的木条,以其中三根的长为边长,制作成一个三角形框架,那么这个框架的周长可能是( )
A. B. C. D.
6.能把一个三角形分成两个面积相等的三角形的是三角形的( )
A.角平分线 B.中线 C.高线 D.重心
7.如图,AD是△ABC的中线,△ABD比△ACD的周长大6 cm,则AB与AC的差为( )
A.2 cm B.3 cm C.6 cm D.12 cm
8.如图, 的三条中线 , , 相交于点G,且四边形 的面积是12,则图中阴影部分的面积为( )
A.16 B.12 C.10 D.6
二、填空题
9.已知三角形的三边分别为2,x,3,那么x的取值范围是
10.自行车的三角形车架可以固定,利用的原理是 .
11.若三角形的周长为13,且三边均为整数,则满足条件的三角形有 种.
12.如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2,则△BDE的面积为 .
13.如图,已知 ,D为BE的中点,则 =
三、解答题
14.若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
15.如图,在四边形中,,平分,.
(1)画出的高;
(2)的面积等于 .
16.如图,已知AD、AE分别是△ABC的高和中线,△ABE的面积为12cm2,AD=4.8cm,∠CAB=90°,AB=6cm.求:
(1)BC的长;
(2)△ABC的周长.
17.已知 △ABC 的周长为 37cm , AD 是 BC 边上的中线, .
(1)如图,当AB=15cm 时,求 BD 的长.
(2)若 ,能否求出 的长?为什么?
参考答案
1.C
2.C
3.B
4.A
5.C
6.B
7.C
8.B
9.1<x<5
10.稳定性
11.5
12.
13.5
14.(1)解:根据三角形的三边关系,
,
解得:3<m<5;
(2)解:因为△ABC的三边均为整数,且3<m<5,所以m=4.
所以,△ABC 的周长为:(m 2)+(2m+1)+8=3m+7=3×4+7=19.
15.(1)解:如图所示,高即为所求;
(2)3
16.(1)解:∵△ABE的面积为12cm2,AD是△ABC的高,AD=4.8cm,
∴=5cm,
∵AE是△ABC的中线,
∴BC=2BE=10cm;
(2)解:∵AD是△ABC的高,AD=4.8cm,BC=10cm,
∴△ABC的面积:=24cm2,
∵在△ABC中,∠CAB=90°,AB=6cm,
∴△ABC的面积:=24cm2
∴AC=8cm,
∴△ABC的周长:AC+BC+AB=24cm.
17.(1)解:∵ , ,
∴ ,
又∵ 的周长为 ,
∴ ,
∴ ,
又∵ 是 边上的中线,
∴ ;
(2)解:不能,理由如下:
∵ , ,
∴ ,
又∵ 的周长为 ,
∴ ,
∴ ,
∴BC+AC=16
