第21章 二次函数与反比例函数 单元练习卷(含答案)2023-2024学年沪科版九年级上册数学上册
文档属性
| 名称 | 第21章 二次函数与反比例函数 单元练习卷(含答案)2023-2024学年沪科版九年级上册数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 286.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 13:42:49 | ||
图片预览



文档简介
第21章《二次函数与反比例函数》单元练习卷
2023-2024学年九年级上册数学沪科版
一、单选题(本大题共12小题,每小题3分,共36分)
1.双曲线有三个点,,,若,则,,的大小关系是( )
A. B.
C. D.
2.二次函数的图象的对称轴是( )
A.直线x= -3 B.直线 x=3 C.直线x= -1 D.直线x=1
3.将二次函数的图象向下平移个单位长度,得到的图象所对应的函数表达式是( )
A. B. C. D.
4.烟花厂为建党成立100周年特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣t2+8t.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
5.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放单车辆,若第二个月的增长率是,第三个月的增长率是第二个月的两倍,那么与的函数关系是 ( )
A. B.
C. D.
6.如图,点B在反比例函数的图象上,轴于点A,连接OB,则△OAB的面积是( )
A. B. C.3 D.6
7.若二次函数的图象与轴有两个交点,则的取值范围是( )
A. B. C.且 D.且
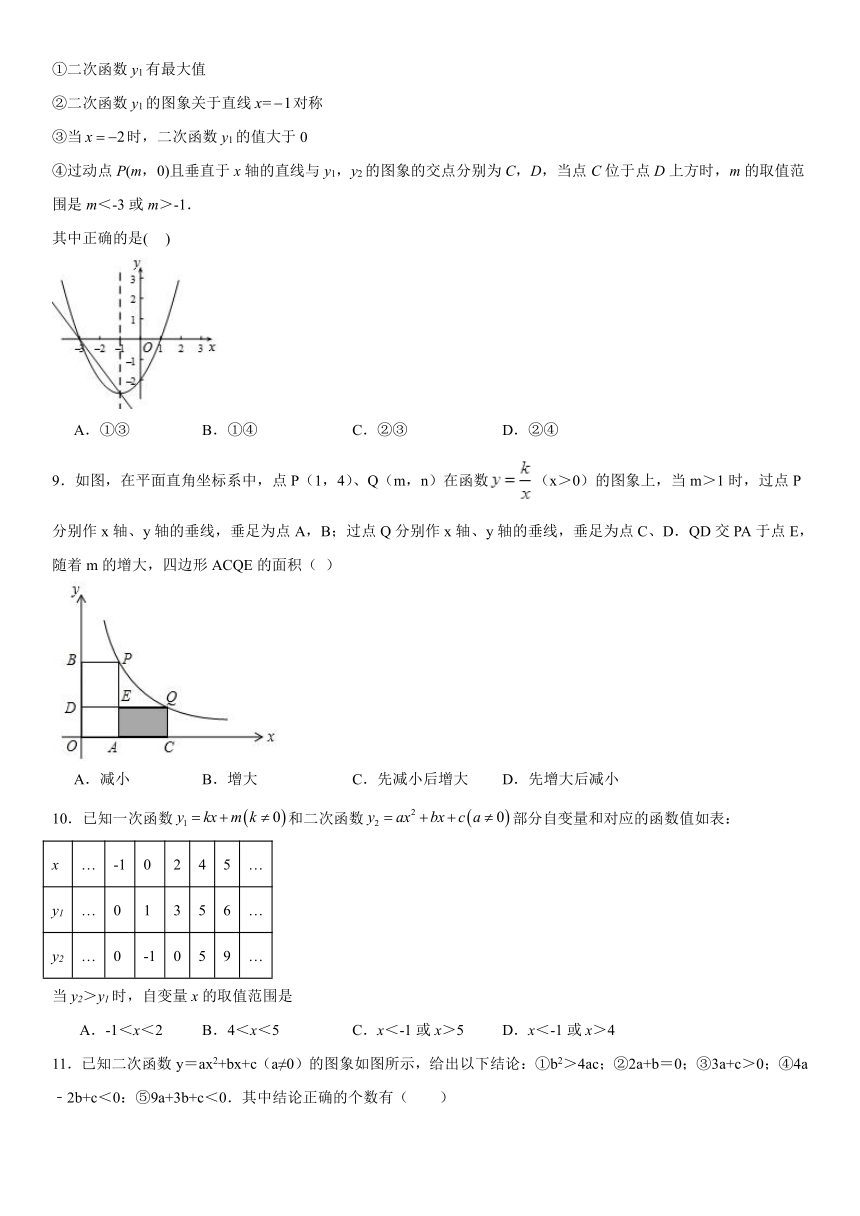
8.已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:
①二次函数y1有最大值
②二次函数y1的图象关于直线对称
③当时,二次函数y1的值大于0
④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<-3或m>-1.
其中正确的是( )
A.①③ B.①④ C.②③ D.②④
9.如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
A.减小 B.增大 C.先减小后增大 D.先增大后减小
10.已知一次函数和二次函数部分自变量和对应的函数值如表:
x … -1 0 2 4 5 …
y1 … 0 1 3 5 6 …
y2 … 0 -1 0 5 9 …
当y2>y1时,自变量x的取值范围是
A.-1<x<2 B.4<x<5 C.x<-1或x>5 D.x<-1或x>4
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②2a+b=0;③3a+c>0;④4a﹣2b+c<0:⑤9a+3b+c<0.其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
12.如图:点P(x,y)为平面直角坐标系内一点,PB⊥x 轴,垂足为B, A为(0,2),若PA=PB,则以下结论正确的是( ).
A.点P在直线上 B.点P在抛物线上
C.点P在抛物线上 D.点P在抛物线上
二、填空题(本大题共8小题,每小题3分,共24分)
13.若点,,在反比例函数为常数)的图象上,则的大小关系是 .
14.如图, 已知拋物线 经过 、 三点, 直线是拋物线的对称轴, 点是直线上的一个动点, 当点到点 点的距离之和最短时, 点的坐标为 .
15.如图,矩形的顶点、分别在、轴的正半轴上,点为对角线的中点,反比例函数在第一象限内的图象经过点,且与、分别交于、两点,若四边形的面积为,则的值为 .
16.如图,正比例函数与反比例函数的图象有一个交点,轴于点.平移直线,使其经过点,得到直线,则直线对应的函数表达式是
17.抛物线的形状大小、开口方向都与y=﹣12x2相同且顶点为(1,﹣2),则该抛物线的解析式为 .
18.若函数的图象与反比例函数的图象没有公共点,则实数k的取值范围是
19.如图,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况,实验数据记录如下:
则y与x之间的函数关系为 .
20.方程(是实数)有两个实根、,且,,那么的取值范围是 .
三、解答题(本大题共5小题,每小题8分,共40分)
21.已知:二次函数.
(1)求这个二次函数图像的对称轴;
(2)若该二次函数图像抛物线开口向上,当时,的最小值是,求当时,的最大值;
(3)若点,在抛物线上,且,求的取值范围.
22.已知抛物线经过两点,,C是抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)点在平面直角坐标系第一象限内的抛物线上运动,设四边形ABDC的面积为S,求S关于m的函数关系式,并求出当m为何值时,S的最大值是多少?
23.已知:反比例函数的图象过点.
(1)求反比例函数的解析式;
(2)若点在该函数图象上,求m的值.
24.如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3,1)、C(-3,0)、O(0,0).将此矩形沿着过E(-,1)、
F(-,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
(1)求折痕所在直线EF的解析式;
(2)一抛物线经过B、E、B′三点,求此二次函数解析式;
(3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.
25.某商店经销一种销售成本为30元/kg的水产品,据市场分析:若按50元/kg销售,一个月能售出300kg,销售单价每涨1元,月销售量就减少10kg.针对这种水产品,请解答以下问题:
(1)设售价为x元/kg,月销售量ykg,请问售价涨了 元,月销售量y(kg)与售价x(元/kg)之间的函数解析式为 .
(2)当售价定为多少时,月销售利润最大?最大利润是多少?
(3)商店想在月销售成本不超过6000元的情况下,使得月销售利润不少于4000元,销售单价可定在什么范围?
参考答案:
1.C
2.B
3.C
4.D
5.A
6.B
7.D
8.D
9.B
10.D
11.C
12.C
13.
14.
15.
16.
17.
18.
19.
20.或
21.(1)
(2)
(3)
22.(1)
(2)S关于m的函数关系式为;当时,S的最大值是
23.(1)
(2)4
24.(1)y=x+4(2)y=x2x-2(3)能;点P的坐标为(,)
25.(1),,(2)当售价定为元时,月销售利润最大,最大利润是元;(3)
2023-2024学年九年级上册数学沪科版
一、单选题(本大题共12小题,每小题3分,共36分)
1.双曲线有三个点,,,若,则,,的大小关系是( )
A. B.
C. D.
2.二次函数的图象的对称轴是( )
A.直线x= -3 B.直线 x=3 C.直线x= -1 D.直线x=1
3.将二次函数的图象向下平移个单位长度,得到的图象所对应的函数表达式是( )
A. B. C. D.
4.烟花厂为建党成立100周年特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣t2+8t.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
5.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放单车辆,若第二个月的增长率是,第三个月的增长率是第二个月的两倍,那么与的函数关系是 ( )
A. B.
C. D.
6.如图,点B在反比例函数的图象上,轴于点A,连接OB,则△OAB的面积是( )
A. B. C.3 D.6
7.若二次函数的图象与轴有两个交点,则的取值范围是( )
A. B. C.且 D.且
8.已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:
①二次函数y1有最大值
②二次函数y1的图象关于直线对称
③当时,二次函数y1的值大于0
④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<-3或m>-1.
其中正确的是( )
A.①③ B.①④ C.②③ D.②④
9.如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
A.减小 B.增大 C.先减小后增大 D.先增大后减小
10.已知一次函数和二次函数部分自变量和对应的函数值如表:
x … -1 0 2 4 5 …
y1 … 0 1 3 5 6 …
y2 … 0 -1 0 5 9 …
当y2>y1时,自变量x的取值范围是
A.-1<x<2 B.4<x<5 C.x<-1或x>5 D.x<-1或x>4
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②2a+b=0;③3a+c>0;④4a﹣2b+c<0:⑤9a+3b+c<0.其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
12.如图:点P(x,y)为平面直角坐标系内一点,PB⊥x 轴,垂足为B, A为(0,2),若PA=PB,则以下结论正确的是( ).
A.点P在直线上 B.点P在抛物线上
C.点P在抛物线上 D.点P在抛物线上
二、填空题(本大题共8小题,每小题3分,共24分)
13.若点,,在反比例函数为常数)的图象上,则的大小关系是 .
14.如图, 已知拋物线 经过 、 三点, 直线是拋物线的对称轴, 点是直线上的一个动点, 当点到点 点的距离之和最短时, 点的坐标为 .
15.如图,矩形的顶点、分别在、轴的正半轴上,点为对角线的中点,反比例函数在第一象限内的图象经过点,且与、分别交于、两点,若四边形的面积为,则的值为 .
16.如图,正比例函数与反比例函数的图象有一个交点,轴于点.平移直线,使其经过点,得到直线,则直线对应的函数表达式是
17.抛物线的形状大小、开口方向都与y=﹣12x2相同且顶点为(1,﹣2),则该抛物线的解析式为 .
18.若函数的图象与反比例函数的图象没有公共点,则实数k的取值范围是
19.如图,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况,实验数据记录如下:
则y与x之间的函数关系为 .
20.方程(是实数)有两个实根、,且,,那么的取值范围是 .
三、解答题(本大题共5小题,每小题8分,共40分)
21.已知:二次函数.
(1)求这个二次函数图像的对称轴;
(2)若该二次函数图像抛物线开口向上,当时,的最小值是,求当时,的最大值;
(3)若点,在抛物线上,且,求的取值范围.
22.已知抛物线经过两点,,C是抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)点在平面直角坐标系第一象限内的抛物线上运动,设四边形ABDC的面积为S,求S关于m的函数关系式,并求出当m为何值时,S的最大值是多少?
23.已知:反比例函数的图象过点.
(1)求反比例函数的解析式;
(2)若点在该函数图象上,求m的值.
24.如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3,1)、C(-3,0)、O(0,0).将此矩形沿着过E(-,1)、
F(-,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
(1)求折痕所在直线EF的解析式;
(2)一抛物线经过B、E、B′三点,求此二次函数解析式;
(3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.
25.某商店经销一种销售成本为30元/kg的水产品,据市场分析:若按50元/kg销售,一个月能售出300kg,销售单价每涨1元,月销售量就减少10kg.针对这种水产品,请解答以下问题:
(1)设售价为x元/kg,月销售量ykg,请问售价涨了 元,月销售量y(kg)与售价x(元/kg)之间的函数解析式为 .
(2)当售价定为多少时,月销售利润最大?最大利润是多少?
(3)商店想在月销售成本不超过6000元的情况下,使得月销售利润不少于4000元,销售单价可定在什么范围?
参考答案:
1.C
2.B
3.C
4.D
5.A
6.B
7.D
8.D
9.B
10.D
11.C
12.C
13.
14.
15.
16.
17.
18.
19.
20.或
21.(1)
(2)
(3)
22.(1)
(2)S关于m的函数关系式为;当时,S的最大值是
23.(1)
(2)4
24.(1)y=x+4(2)y=x2x-2(3)能;点P的坐标为(,)
25.(1),,(2)当售价定为元时,月销售利润最大,最大利润是元;(3)
