第十一章 三角形 单元练习(含答案)2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 单元练习(含答案)2023—2024学年人教版数学八年级上册 | 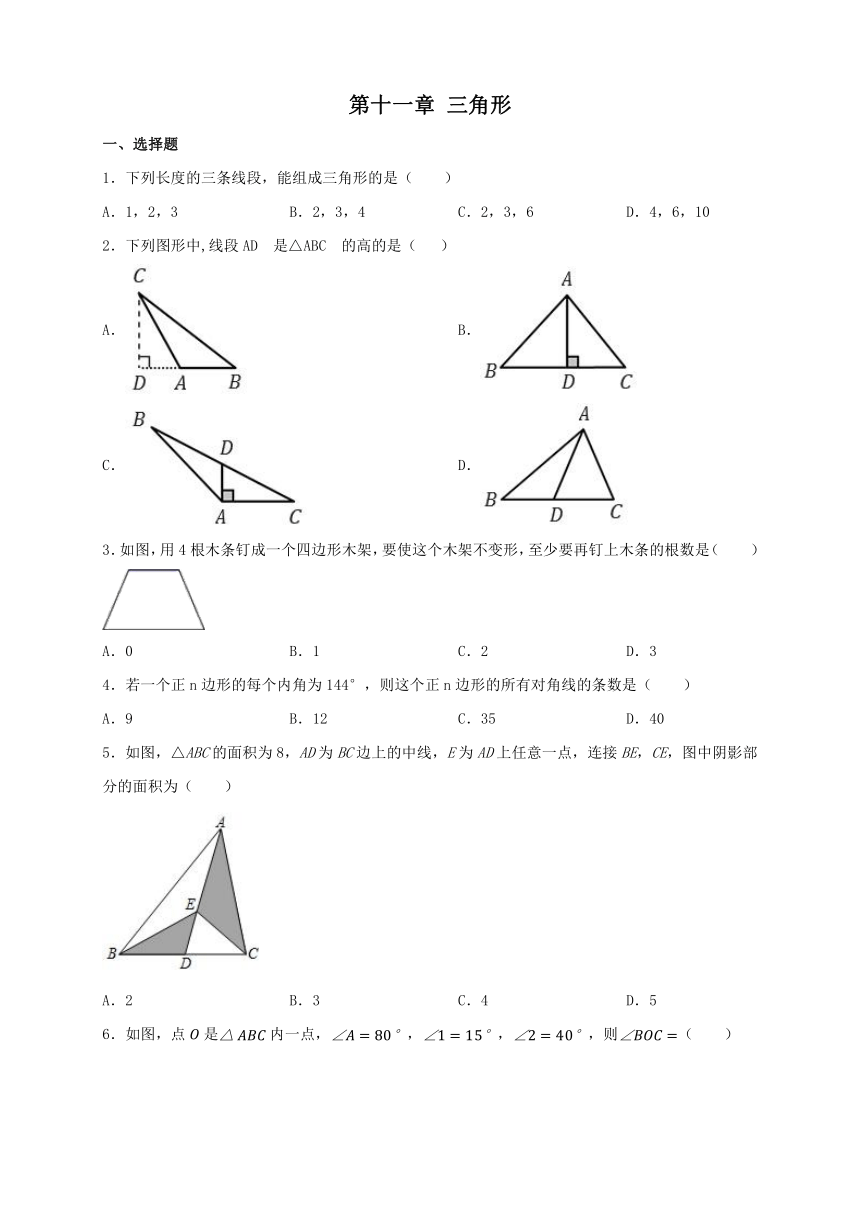 | |
| 格式 | docx | ||
| 文件大小 | 104.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 13:48:31 | ||
图片预览

文档简介
第十一章 三角形
一、选择题
1.下列长度的三条线段,能组成三角形的是( )
A.1,2,3 B.2,3,4 C.2,3,6 D.4,6,10
2.下列图形中,线段AD 是△ABC 的高的是( )
A. B.
C. D.
3.如图,用4根木条钉成一个四边形木架,要使这个木架不变形,至少要再钉上木条的根数是( )
A.0 B.1 C.2 D.3
4.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.9 B.12 C.35 D.40
5.如图,△ABC的面积为8,AD为BC边上的中线,E为AD上任意一点,连接BE,CE,图中阴影部分的面积为( )
A.2 B.3 C.4 D.5
6.如图,点是内一点,,,,则( )
A. B. C. D.
7.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
8.如图,足球图片中的一块黑色皮块的内角和是( )
A.720° B.540° C.360° D.180°
二、填空题
9.已知三角形的三边长分别为4,8,a,则a的取值范围是 .
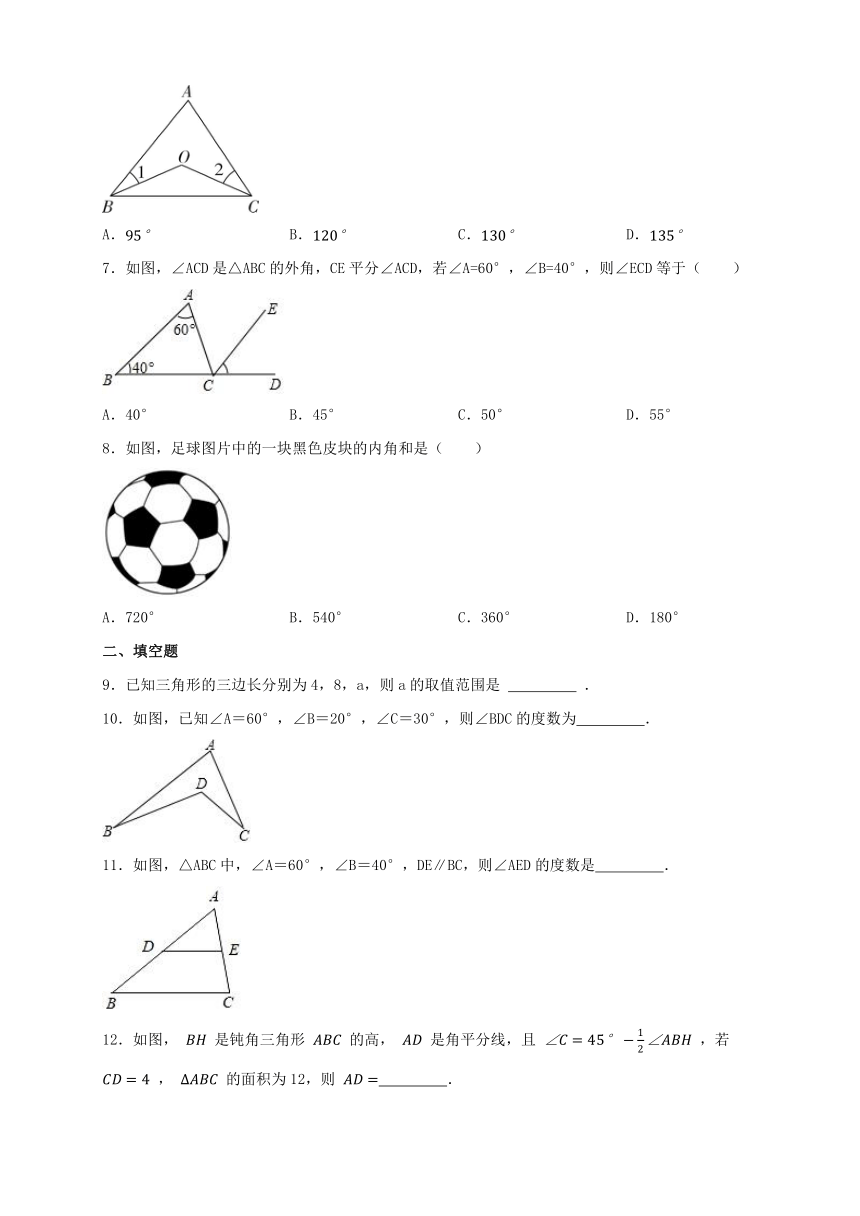
10.如图,已知∠A=60°,∠B=20°,∠C=30°,则∠BDC的度数为 .
11.如图,△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是 .
12.如图, 是钝角三角形 的高, 是角平分线,且 ,若 , 的面积为12,则 .
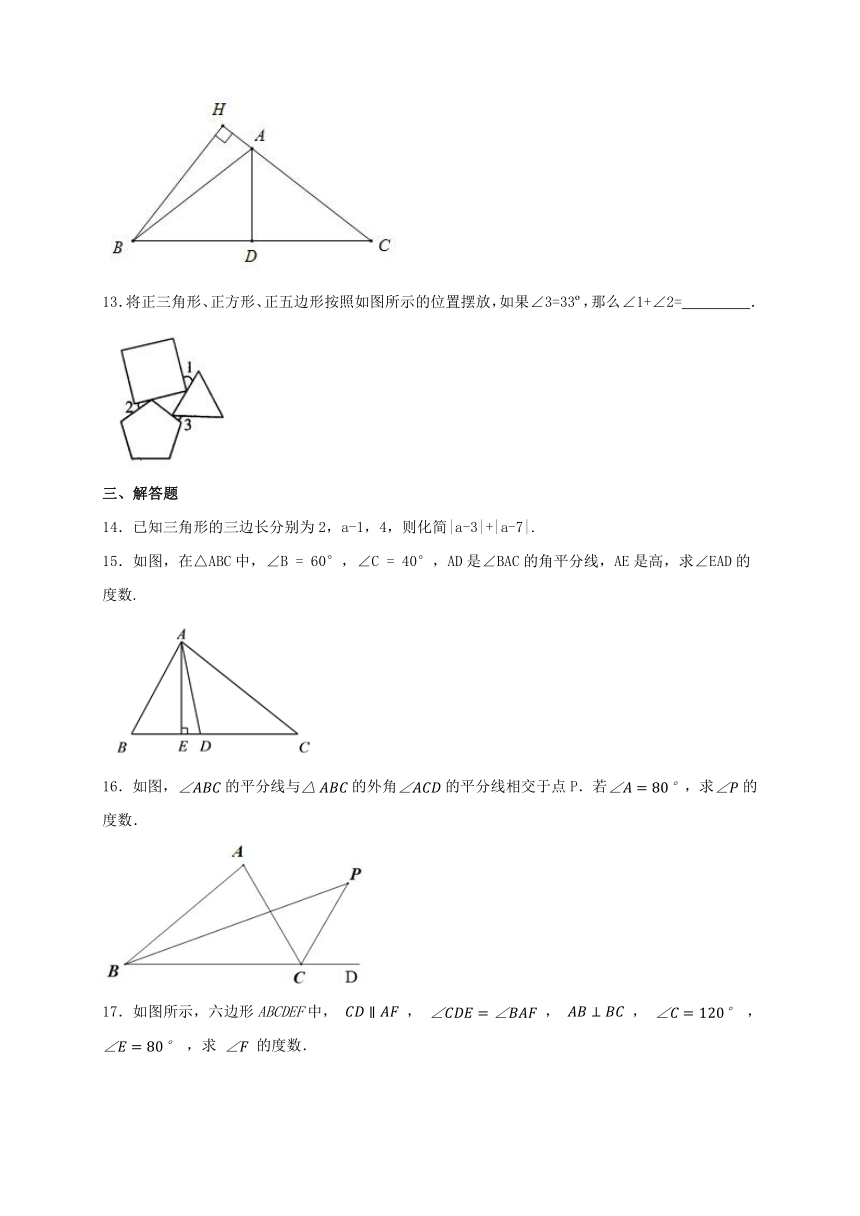
13.将正三角形、正方形、正五边形按照如图所示的位置摆放,如果∠3=33 ,那么∠1+∠2= .
三、解答题
14.已知三角形的三边长分别为2,a-1,4,则化简|a-3|+|a-7|.
15.如图,在△ABC中,∠B = 60°,∠C = 40°,AD是∠BAC的角平分线,AE是高,求∠EAD的度数.
16.如图,的平分线与的外角的平分线相交于点P.若,求的度数.
17.如图所示,六边形ABCDEF中, , , , , ,求 的度数.
18.如图,△ABC中,高BD、CE相交于点H,若∠A:∠ABC:∠ACB=3:2:4,则∠BHC为多少度?
参考答案
1.B
2.B
3.B
4.C
5.C
6.D
7.C
8.B
9.410.110°
11.80°
12.3
13.69
14.解:由三角形三边关系得: 2得 3则原式=a-3+7-a=4.
15.解:∵∠B=60°,∠C=40°,
∴∠BAC=180°-∠B-∠C=180°-60°-40°=80°,
∵AD是角平分线,
∴∠BAD= ∠BAC= ×80°=40°,
∵AE是高,
∴∠BEA=90°
∴∠BAE=90°-∠B=90°-60°=30°,
∴∠EAD=∠BAD-∠BAE=40°-30°=10°.
16.解:∵是的外角,
∴,
∵平分,平分,
∴,,
∵是的外角,
∴,
∴,
∴,
∴,
∵,
∴.
17.解:连接AD
在四边形ABCD中, .
, .
又 , .
, .
.
.
在六边形ABCDEF中, ,
又 , , ,
.
18.解:∵∠A:∠ABC:∠ACB=3:2:4,
设∠A=3x,∠ABC=2x,∠ACB=4x,
∴3x+2x+4x=180°
解之:x=20°.
∴∠A=3×20°=60°.
∵高BD、CE相交于点H,
∴∠AEH=∠ADH=90°,
∴∠EHD=∠BHC=360°-∠A-∠AEH-∠ADH=360°-60°-90°-90°=120°.
一、选择题
1.下列长度的三条线段,能组成三角形的是( )
A.1,2,3 B.2,3,4 C.2,3,6 D.4,6,10
2.下列图形中,线段AD 是△ABC 的高的是( )
A. B.
C. D.
3.如图,用4根木条钉成一个四边形木架,要使这个木架不变形,至少要再钉上木条的根数是( )
A.0 B.1 C.2 D.3
4.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.9 B.12 C.35 D.40
5.如图,△ABC的面积为8,AD为BC边上的中线,E为AD上任意一点,连接BE,CE,图中阴影部分的面积为( )
A.2 B.3 C.4 D.5
6.如图,点是内一点,,,,则( )
A. B. C. D.
7.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
8.如图,足球图片中的一块黑色皮块的内角和是( )
A.720° B.540° C.360° D.180°
二、填空题
9.已知三角形的三边长分别为4,8,a,则a的取值范围是 .
10.如图,已知∠A=60°,∠B=20°,∠C=30°,则∠BDC的度数为 .
11.如图,△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是 .
12.如图, 是钝角三角形 的高, 是角平分线,且 ,若 , 的面积为12,则 .
13.将正三角形、正方形、正五边形按照如图所示的位置摆放,如果∠3=33 ,那么∠1+∠2= .
三、解答题
14.已知三角形的三边长分别为2,a-1,4,则化简|a-3|+|a-7|.
15.如图,在△ABC中,∠B = 60°,∠C = 40°,AD是∠BAC的角平分线,AE是高,求∠EAD的度数.
16.如图,的平分线与的外角的平分线相交于点P.若,求的度数.
17.如图所示,六边形ABCDEF中, , , , , ,求 的度数.
18.如图,△ABC中,高BD、CE相交于点H,若∠A:∠ABC:∠ACB=3:2:4,则∠BHC为多少度?
参考答案
1.B
2.B
3.B
4.C
5.C
6.D
7.C
8.B
9.4
11.80°
12.3
13.69
14.解:由三角形三边关系得: 2
15.解:∵∠B=60°,∠C=40°,
∴∠BAC=180°-∠B-∠C=180°-60°-40°=80°,
∵AD是角平分线,
∴∠BAD= ∠BAC= ×80°=40°,
∵AE是高,
∴∠BEA=90°
∴∠BAE=90°-∠B=90°-60°=30°,
∴∠EAD=∠BAD-∠BAE=40°-30°=10°.
16.解:∵是的外角,
∴,
∵平分,平分,
∴,,
∵是的外角,
∴,
∴,
∴,
∴,
∵,
∴.
17.解:连接AD
在四边形ABCD中, .
, .
又 , .
, .
.
.
在六边形ABCDEF中, ,
又 , , ,
.
18.解:∵∠A:∠ABC:∠ACB=3:2:4,
设∠A=3x,∠ABC=2x,∠ACB=4x,
∴3x+2x+4x=180°
解之:x=20°.
∴∠A=3×20°=60°.
∵高BD、CE相交于点H,
∴∠AEH=∠ADH=90°,
∴∠EHD=∠BHC=360°-∠A-∠AEH-∠ADH=360°-60°-90°-90°=120°.
