初二下数学期中复习——平行四边形(1)讲义(无答案)
文档属性
| 名称 | 初二下数学期中复习——平行四边形(1)讲义(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 294.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 17:44:06 | ||
图片预览

文档简介
初二下数学期中复习——平行四边形
班级______姓名____________学号______
【知识梳理】
性质与判定:
平行四边形 矩形 菱形 正方形
性 质 边 对边平行且相等 对边平行且相等 对边平行,四边相等 对边平行,四边相等
角 对角相等 四个角都是直角 对角相等 四个角都是直角
对角线 互相平分 互相平分且相等 互相垂直平分,且每条对角线平分一组对角 互相垂直平分且相等,每条对角线平分一组对角
判定 两组对边分别平行; 两组对边分别相等; 一组对边平行且相等; 两组对角分别相等; 两条对角线互相平分. 有三个角是直角; 是平行四边形且有一个角是直角; 是平行四边形且两条对角线相等. 四边相等; 是平行四边形且有一组邻边相等; 是平行四边形且两条对角线互相垂直. 是矩形,且有一组邻边相等; 是菱形,且有一个角是直角.
轴对称性 否 是,2条 是,2条 是,4条
面积 S= ah S=ab S= S= a2
二.与三角形相关的定理和性质:
1.三角形的中位线定理: .
2.直角三角形的一个重要性质:直角三角形斜边上的中线 .
【巩固练习】
1.若点O是四边形ABCD对角线的交点且OA=OB=OC=OD,则四边形ABCD是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
2.矩形、菱形、正方形都具有的性质的是( )
A.对角线相等 B.对角线互相平分 C.对角线互相垂直 D.对角线平分对角
3.如图,点O是矩形ABCD两对角线的交点,E是AB上的点,沿CE折叠后,
点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A.2 B. C. D.6
4.如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D
作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
A B C D
5.一个平行四边形的一个角为40°,则其他三个角的度数为 ;
它的两条对角线的长度分别为5和7, 则它的一条边长的取值范围是 .
6. 如图,在正方形ABCD内,以AB为边作等边△ABE,则∠BEG=_______°.
7.如图,在平行四边形ABCD中,点M为边AD上一点,AM=2MD,点E,点F分别是BM,CM中点,若EF=6,则AM的长为_____.
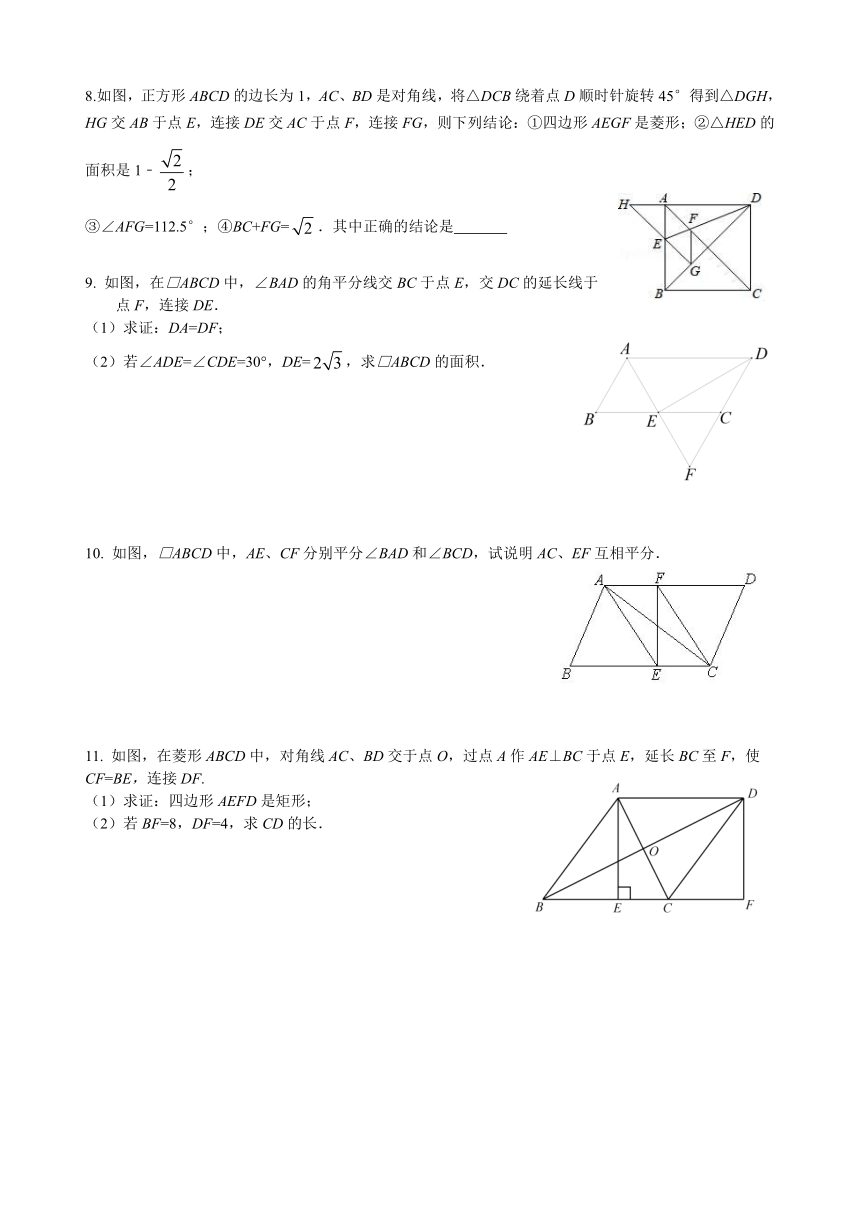
8.如图,正方形ABCD的边长为1,AC、BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG,则下列结论:①四边形AEGF是菱形;②△HED的面积是1﹣;
③∠AFG=112.5°;④BC+FG=.其中正确的结论是
9. 如图,在□ABCD中,∠BAD的角平分线交BC于点E,交DC的延长线于点F,连接DE.
(1)求证:DA=DF;
(2)若∠ADE=∠CDE=30°,DE=,求□ABCD的面积.
10. 如图,□ABCD中,AE、CF分别平分∠BAD和∠BCD,试说明AC、EF互相平分.
11. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于点E,延长BC至F,使
CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)若BF=8,DF=4,求CD的长.
12. 如图,四边形ABCD为矩形,DE∥AC,且DE=AB,过点E作AD的垂线交AC于点F.
(1)依题意补全图,并证明四边形EFCD是菱形;
(2)若AB=3,BC=,求平行线DE与AC间的距离.
13. 如图,在四边形ABCD中,∠DAB=900,∠DCB=900,E、F分别是BD、AC的中点.
求证:EF⊥AC.
14. 如图,在△ABC中,D、E分别为AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q.
求证: AP=AQ.
15. 如图,正方形ABCD中, P为BD上一动点,过点P 作PQ⊥AP交CD边于点Q.
(1)求证:PA=PQ;
(2)用等式表示PB、PD、AQ之间的数量关系,并证明;
(3)点P从点B出发,沿BD方向移动,若移动的路径长为2,则AQ的中点M移动的路径长为 (直接写出答案).
16. 在□ABCD中,O是对角线BD的中点,点E在ABCD外,且∠AED=900.过点C作直线ED的垂线,垂足为F.连接OE,OF.
(1)如图1,当□ABCD为矩形,且∠DAE=450时,画出线段OE与OF,并直接写出这两条线段的数量关系;
(2)在图2中,根据题意补全图形,写出线段OE与OF的数量关系并加以证明;
(3)如图3,当为正方形时,若AE=1,OD=,直接写出OF的长.
班级______姓名____________学号______
【知识梳理】
性质与判定:
平行四边形 矩形 菱形 正方形
性 质 边 对边平行且相等 对边平行且相等 对边平行,四边相等 对边平行,四边相等
角 对角相等 四个角都是直角 对角相等 四个角都是直角
对角线 互相平分 互相平分且相等 互相垂直平分,且每条对角线平分一组对角 互相垂直平分且相等,每条对角线平分一组对角
判定 两组对边分别平行; 两组对边分别相等; 一组对边平行且相等; 两组对角分别相等; 两条对角线互相平分. 有三个角是直角; 是平行四边形且有一个角是直角; 是平行四边形且两条对角线相等. 四边相等; 是平行四边形且有一组邻边相等; 是平行四边形且两条对角线互相垂直. 是矩形,且有一组邻边相等; 是菱形,且有一个角是直角.
轴对称性 否 是,2条 是,2条 是,4条
面积 S= ah S=ab S= S= a2
二.与三角形相关的定理和性质:
1.三角形的中位线定理: .
2.直角三角形的一个重要性质:直角三角形斜边上的中线 .
【巩固练习】
1.若点O是四边形ABCD对角线的交点且OA=OB=OC=OD,则四边形ABCD是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
2.矩形、菱形、正方形都具有的性质的是( )
A.对角线相等 B.对角线互相平分 C.对角线互相垂直 D.对角线平分对角
3.如图,点O是矩形ABCD两对角线的交点,E是AB上的点,沿CE折叠后,
点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A.2 B. C. D.6
4.如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D
作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
A B C D
5.一个平行四边形的一个角为40°,则其他三个角的度数为 ;
它的两条对角线的长度分别为5和7, 则它的一条边长的取值范围是 .
6. 如图,在正方形ABCD内,以AB为边作等边△ABE,则∠BEG=_______°.
7.如图,在平行四边形ABCD中,点M为边AD上一点,AM=2MD,点E,点F分别是BM,CM中点,若EF=6,则AM的长为_____.
8.如图,正方形ABCD的边长为1,AC、BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG,则下列结论:①四边形AEGF是菱形;②△HED的面积是1﹣;
③∠AFG=112.5°;④BC+FG=.其中正确的结论是
9. 如图,在□ABCD中,∠BAD的角平分线交BC于点E,交DC的延长线于点F,连接DE.
(1)求证:DA=DF;
(2)若∠ADE=∠CDE=30°,DE=,求□ABCD的面积.
10. 如图,□ABCD中,AE、CF分别平分∠BAD和∠BCD,试说明AC、EF互相平分.
11. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于点E,延长BC至F,使
CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)若BF=8,DF=4,求CD的长.
12. 如图,四边形ABCD为矩形,DE∥AC,且DE=AB,过点E作AD的垂线交AC于点F.
(1)依题意补全图,并证明四边形EFCD是菱形;
(2)若AB=3,BC=,求平行线DE与AC间的距离.
13. 如图,在四边形ABCD中,∠DAB=900,∠DCB=900,E、F分别是BD、AC的中点.
求证:EF⊥AC.
14. 如图,在△ABC中,D、E分别为AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q.
求证: AP=AQ.
15. 如图,正方形ABCD中, P为BD上一动点,过点P 作PQ⊥AP交CD边于点Q.
(1)求证:PA=PQ;
(2)用等式表示PB、PD、AQ之间的数量关系,并证明;
(3)点P从点B出发,沿BD方向移动,若移动的路径长为2,则AQ的中点M移动的路径长为 (直接写出答案).
16. 在□ABCD中,O是对角线BD的中点,点E在ABCD外,且∠AED=900.过点C作直线ED的垂线,垂足为F.连接OE,OF.
(1)如图1,当□ABCD为矩形,且∠DAE=450时,画出线段OE与OF,并直接写出这两条线段的数量关系;
(2)在图2中,根据题意补全图形,写出线段OE与OF的数量关系并加以证明;
(3)如图3,当为正方形时,若AE=1,OD=,直接写出OF的长.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
