2023-2024学年北师大版九年级数学上册1.2 矩形的性质与判定 同步练习题(含3课时,无答案)
文档属性
| 名称 | 2023-2024学年北师大版九年级数学上册1.2 矩形的性质与判定 同步练习题(含3课时,无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 15:54:49 | ||
图片预览

文档简介
1.2 矩形的性质与判定 同步练习题 2023-2024学年北师大版九年级数学上册
第1课时 矩形的性质与判定(1)
A组基础过关
一、选择题
1.下列是矩形与菱形都具有的性质是( )
A.各角都相等 B.各边都相等 C.对角线相等 D.有两条对称轴
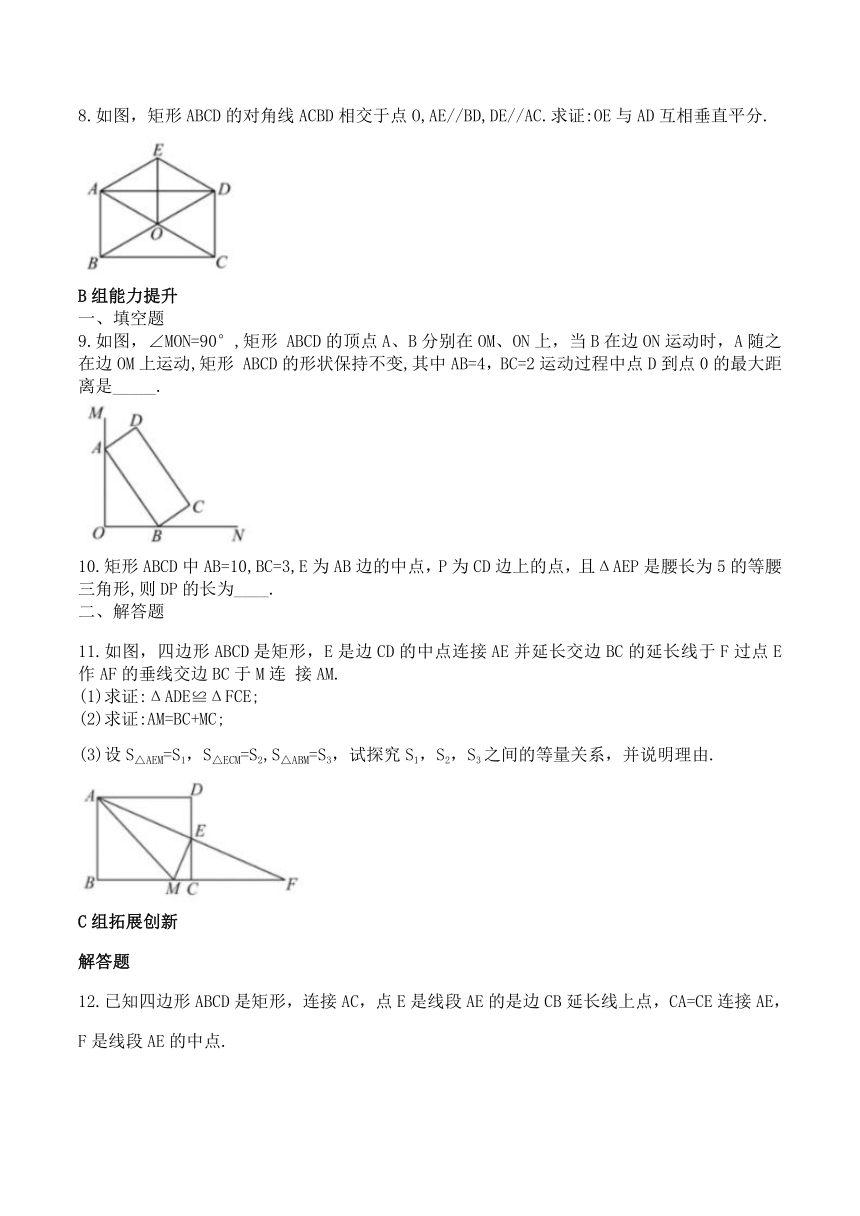
2.如图,将矩形ABCD折叠,AE是折痕,点D恰好落在BC边上的点F处,量得∠BAF=50°,那么∠DEA等于 ( )
A.40° B.50° C.60° D.70°
3.如图,矩形ABCD的两条对角线相交于点0,∠AOD=60°AD=2,则AC的长是( )
A.2 B.4 C.2 D.4
二、填空题
4.在△ABC中,∠C=90°,D为AB的中点,若CD=5,BC=5,则AC=____.
5.直角三角形斜边上的高与中线分别为8cm和10cm,则它的面积是______cm2.
6.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为___.
三、解答题
7.如图,在ΔABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于点G.
(1)求证:G是CE的中点;
(2)若∠B=70°求∠BCE的度数
8.如图,矩形ABCD的对角线ACBD相交于点O,AE//BD,DE//AC.求证:OE与AD互相垂直平分.
B组能力提升
一、填空题
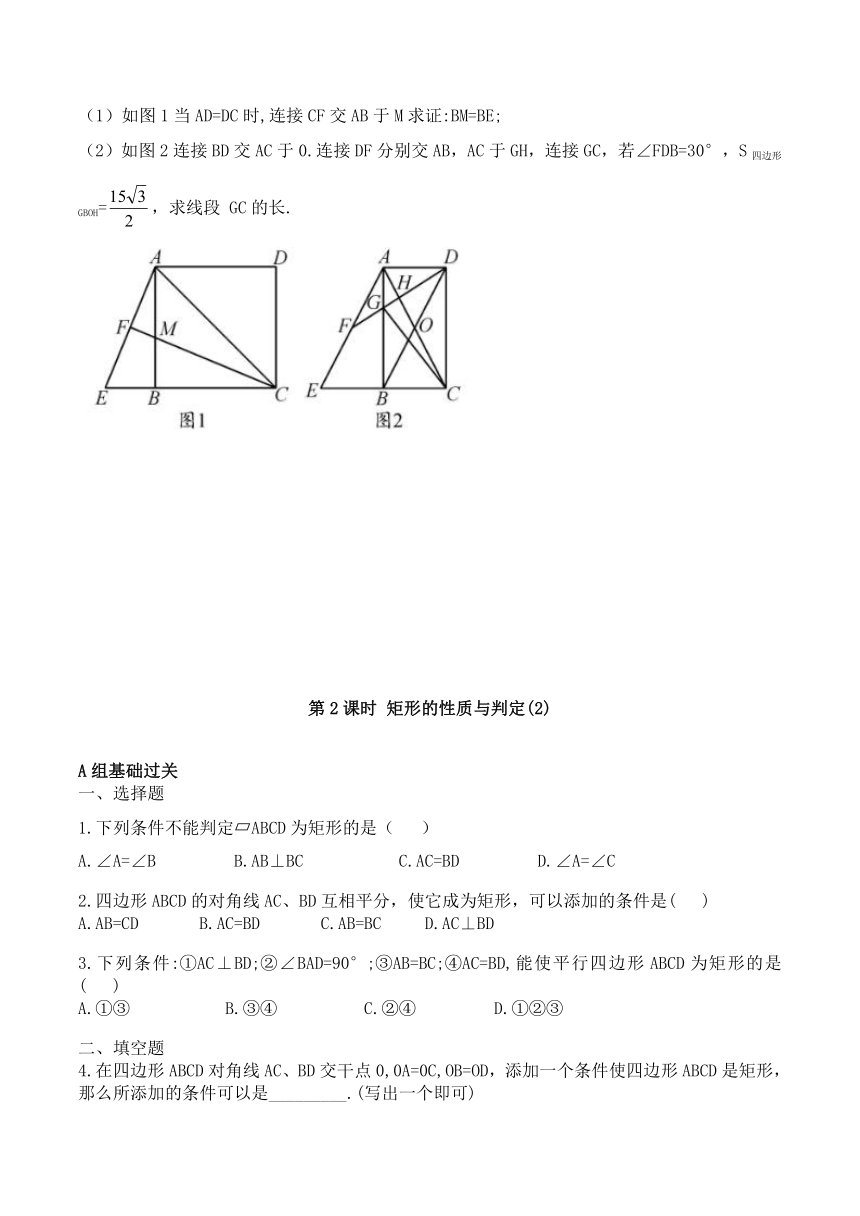
9.如图,∠MON=90°,矩形 ABCD的顶点A、B分别在OM、ON上,当B在边ON运动时,A随之在边OM上运动,矩形 ABCD的形状保持不变,其中AB=4,BC=2运动过程中点D到点0的最大距离是_____.
10.矩形ABCD中AB=10,BC=3,E为AB边的中点,P为CD边上的点,且ΔAEP是腰长为5的等腰三角形,则DP的长为____.
二、解答题
11.如图,四边形ABCD是矩形,E是边CD的中点连接AE并延长交边BC的延长线于F过点E作AF的垂线交边BC于M连 接AM.
(1)求证:ΔADE≌ΔFCE;
(2)求证:AM=BC+MC;
(3)设S△AEM=S1,S△ECM=S2,S△ABM=S3,试探究S1,S2,S3之间的等量关系,并说明理由.
C组拓展创新
解答题
12.已知四边形ABCD是矩形,连接AC,点E是线段AE的是边CB延长线上点,CA=CE连接AE,
F是线段AE的中点.
如图1当AD=DC时,连接CF交AB于M求证:BM=BE;
(2)如图2连接BD交AC于0.连接DF分别交AB,AC于GH,连接GC,若∠FDB=30°,S四边形GBOH=,求线段 GC的长.
第2课时 矩形的性质与判定(2)
A组基础过关
一、选择题
1.下列条件不能判定 ABCD为矩形的是( )
A.∠A=∠B B.AB⊥BC C.AC=BD D.∠A=∠C
2.四边形ABCD的对角线AC、BD互相平分,使它成为矩形,可以添加的条件是( )
A.AB=CD B.AC=BD C.AB=BC D.AC⊥BD
3.下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD,能使平行四边形ABCD为矩形的是 ( )
A.①③ B.③④ C.②④ D.①②③
二、填空题
4.在四边形ABCD对角线AC、BD交干点0,0A=0C,OB=OD,添加一个条件使四边形ABCD是矩形,那么所添加的条件可以是_________.(写出一个即可)
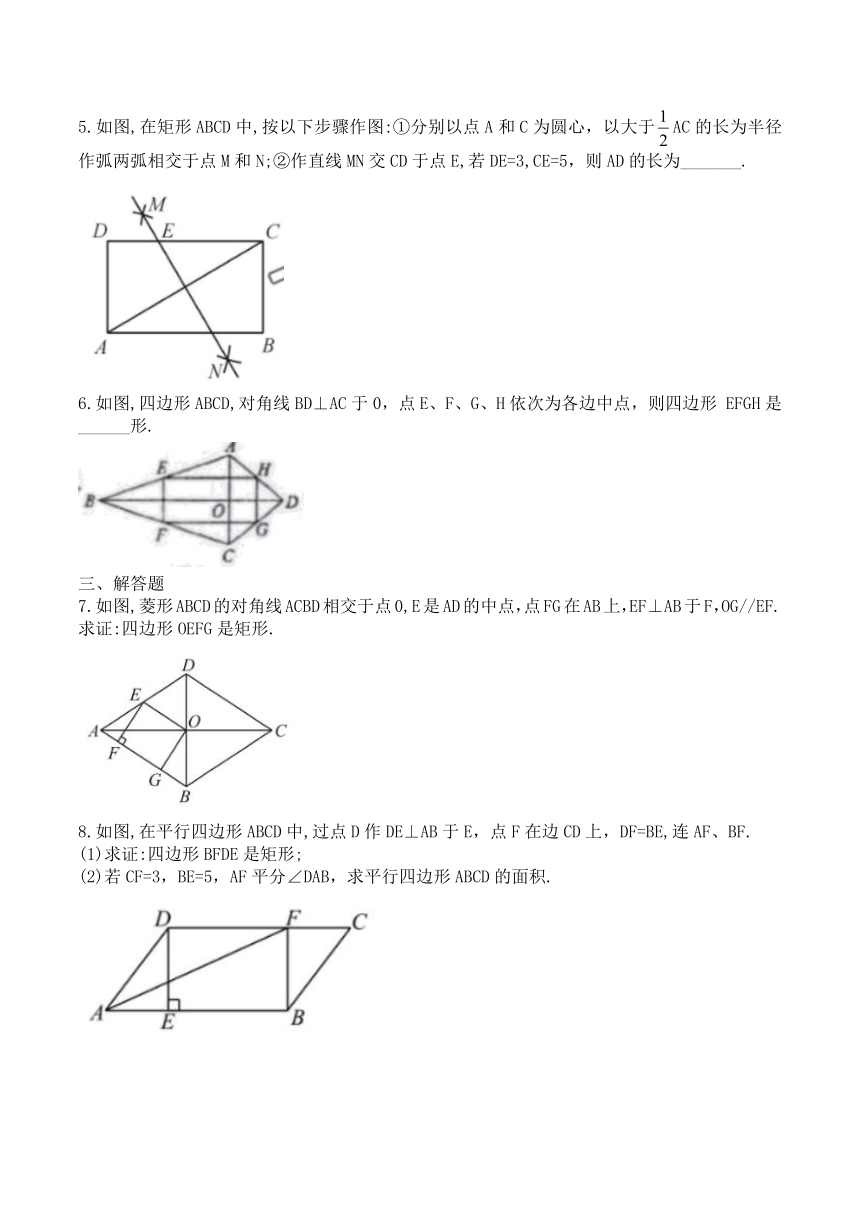
5.如图,在矩形ABCD中,按以下步骤作图:①分别以点A和C为圆心,以大于AC的长为半径作弧两弧相交于点M和N;②作直线MN交CD于点E,若DE=3,CE=5,则AD的长为_______.
6.如图,四边形ABCD,对角线BD⊥AC于0,点E、F、G、H依次为各边中点,则四边形 EFGH是______形.
三、解答题
7.如图,菱形ABCD的对角线ACBD相交于点0,E是AD的中点,点FG在AB上,EF⊥AB于F,OG//EF.求证:四边形OEFG是矩形.
8.如图,在平行四边形ABCD中,过点D作DE⊥AB于E,点F在边CD上,DF=BE,连AF、BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四边形ABCD的面积.
B组能力提升
一、填空题
9.如图,在矩形ABCD中,BC=20cm,点P和 点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快______s时,四边形ABPQ成为矩形.
10.如图,在RtΔABC中,∠C=90°AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC分别在边于点D,PE⊥CB于点E,连接DE,则DE的最小值为_______.
二、解答题
11.如图,在△ABC中点0是边AC上一个动点,过点0作直线EF//BC分别交∠ACB和外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求0C的长.
(2)连接AE,AF,当点0在边AC上运到什么位置时,四边形AECF是矩形 说明理由.
C组拓展创新
解答题
12.如图,在平面直角坐标系中,矩形OABC的顶点0为坐标原点,顶点A、C分别在x轴正半轴和y轴正半轴上,顶点B的坐标为(12,8),直线y=kx+8-6k(k<0)交边AB于点P,交边BC于点Q.
(1)当k=-1时,求点P,Q的坐标;
(2)若直线PQ//AC,,BH是Rt△BPQ斜边PQ上的高,求BH的长;
(3)若PQ平分∠OPB,求k的值.
第3课 时矩形的性质与判定(3)
A组基础过关
一、选择题
1.如图,四边形ABCD和四边形AEFG都是矩形.若∠BAG=20°则∠DGF等于( )
A.70° B.60° C.80° D.45°
2.下列各组条件中,能判定四边形ABCD为矩形的是( )
A.∠A+∠B=90° B.AB//CD,AB=CD,AC=BD C.AB//CD,AD=BC,AC=BD D.AC=BD,∠A=90°
3.矩形的一条边和一条对角线的夹角是40°,则两条对角线所夹的锐角等于( )
A.50° B.60 C.70° D.80°
二、填空题
4.矩形的面积为12cm ,一条边长为3cm,则矩形的对角线长为______.
5.如图,矩形ABCD中点E F分别是AB,CD的中点,连接DE和BF,分别取DE,BF的中点MN连接AM、CN、MN,若AB=2,BC=2,则图中阴影部分的面积为________.
6.如图,点O是菱形ABCD对角线的交点,DE//AC,CE//BD,连接OE,设AC=12 BD=16,则OE的长为________.
三、解答题
7.如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD.连接AC、CE、EF、AF.
(1)求证:四边形ACEF是矩形; (2)求四边形ACEF的周长.
8.如图,四边形ABCD中,对角线ACBD相交于点0,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形;
(2)若DE⊥AC交BC于E,∠ADB:∠CDB=2:3.则∠BDE的度数是多少
B组能力提升
一、填空题
9.如图,矩形OABC的顶点A.C 分别在坐标轴上B(8,7) D(5,0),点P是边AB或边BC上的一点,连接OP,DP,当△ODP为等腰三角形时,点P的坐标为________.
10.如图,在矩形ABCD中,E,F分别是边AB、AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=6,则GH的最小值是_______.
二、解答题
11.如图,在RtΔABC中,∠ACB=90°D是线段AB上一点,DE//BC,DF//AC,连接EF.CD.
(1)求证:EF=CD
(2)当D在线段AB的_______位置时,S矩形DECF =S△ABC.
(3)当CD与AB满足什么条件时,EF最短
C组拓展创新
解答题
12.如图1.已知AD//BC,AB//DC,∠B=∠C.
(1)求证:四边形ABCD为矩形;
(2)如图2,M为AD的中点,在AB上取一点N,使∠BNC=2∠DCM.
(i)若N为AB中点,BN=2,求CN的长;
(ii)若CM=3,CN=4,求BC的长.
第1课时 矩形的性质与判定(1)
A组基础过关
一、选择题
1.下列是矩形与菱形都具有的性质是( )
A.各角都相等 B.各边都相等 C.对角线相等 D.有两条对称轴
2.如图,将矩形ABCD折叠,AE是折痕,点D恰好落在BC边上的点F处,量得∠BAF=50°,那么∠DEA等于 ( )
A.40° B.50° C.60° D.70°
3.如图,矩形ABCD的两条对角线相交于点0,∠AOD=60°AD=2,则AC的长是( )
A.2 B.4 C.2 D.4
二、填空题
4.在△ABC中,∠C=90°,D为AB的中点,若CD=5,BC=5,则AC=____.
5.直角三角形斜边上的高与中线分别为8cm和10cm,则它的面积是______cm2.
6.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为___.
三、解答题
7.如图,在ΔABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于点G.
(1)求证:G是CE的中点;
(2)若∠B=70°求∠BCE的度数
8.如图,矩形ABCD的对角线ACBD相交于点O,AE//BD,DE//AC.求证:OE与AD互相垂直平分.
B组能力提升
一、填空题
9.如图,∠MON=90°,矩形 ABCD的顶点A、B分别在OM、ON上,当B在边ON运动时,A随之在边OM上运动,矩形 ABCD的形状保持不变,其中AB=4,BC=2运动过程中点D到点0的最大距离是_____.
10.矩形ABCD中AB=10,BC=3,E为AB边的中点,P为CD边上的点,且ΔAEP是腰长为5的等腰三角形,则DP的长为____.
二、解答题
11.如图,四边形ABCD是矩形,E是边CD的中点连接AE并延长交边BC的延长线于F过点E作AF的垂线交边BC于M连 接AM.
(1)求证:ΔADE≌ΔFCE;
(2)求证:AM=BC+MC;
(3)设S△AEM=S1,S△ECM=S2,S△ABM=S3,试探究S1,S2,S3之间的等量关系,并说明理由.
C组拓展创新
解答题
12.已知四边形ABCD是矩形,连接AC,点E是线段AE的是边CB延长线上点,CA=CE连接AE,
F是线段AE的中点.
如图1当AD=DC时,连接CF交AB于M求证:BM=BE;
(2)如图2连接BD交AC于0.连接DF分别交AB,AC于GH,连接GC,若∠FDB=30°,S四边形GBOH=,求线段 GC的长.
第2课时 矩形的性质与判定(2)
A组基础过关
一、选择题
1.下列条件不能判定 ABCD为矩形的是( )
A.∠A=∠B B.AB⊥BC C.AC=BD D.∠A=∠C
2.四边形ABCD的对角线AC、BD互相平分,使它成为矩形,可以添加的条件是( )
A.AB=CD B.AC=BD C.AB=BC D.AC⊥BD
3.下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD,能使平行四边形ABCD为矩形的是 ( )
A.①③ B.③④ C.②④ D.①②③
二、填空题
4.在四边形ABCD对角线AC、BD交干点0,0A=0C,OB=OD,添加一个条件使四边形ABCD是矩形,那么所添加的条件可以是_________.(写出一个即可)
5.如图,在矩形ABCD中,按以下步骤作图:①分别以点A和C为圆心,以大于AC的长为半径作弧两弧相交于点M和N;②作直线MN交CD于点E,若DE=3,CE=5,则AD的长为_______.
6.如图,四边形ABCD,对角线BD⊥AC于0,点E、F、G、H依次为各边中点,则四边形 EFGH是______形.
三、解答题
7.如图,菱形ABCD的对角线ACBD相交于点0,E是AD的中点,点FG在AB上,EF⊥AB于F,OG//EF.求证:四边形OEFG是矩形.
8.如图,在平行四边形ABCD中,过点D作DE⊥AB于E,点F在边CD上,DF=BE,连AF、BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四边形ABCD的面积.
B组能力提升
一、填空题
9.如图,在矩形ABCD中,BC=20cm,点P和 点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快______s时,四边形ABPQ成为矩形.
10.如图,在RtΔABC中,∠C=90°AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC分别在边于点D,PE⊥CB于点E,连接DE,则DE的最小值为_______.
二、解答题
11.如图,在△ABC中点0是边AC上一个动点,过点0作直线EF//BC分别交∠ACB和外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求0C的长.
(2)连接AE,AF,当点0在边AC上运到什么位置时,四边形AECF是矩形 说明理由.
C组拓展创新
解答题
12.如图,在平面直角坐标系中,矩形OABC的顶点0为坐标原点,顶点A、C分别在x轴正半轴和y轴正半轴上,顶点B的坐标为(12,8),直线y=kx+8-6k(k<0)交边AB于点P,交边BC于点Q.
(1)当k=-1时,求点P,Q的坐标;
(2)若直线PQ//AC,,BH是Rt△BPQ斜边PQ上的高,求BH的长;
(3)若PQ平分∠OPB,求k的值.
第3课 时矩形的性质与判定(3)
A组基础过关
一、选择题
1.如图,四边形ABCD和四边形AEFG都是矩形.若∠BAG=20°则∠DGF等于( )
A.70° B.60° C.80° D.45°
2.下列各组条件中,能判定四边形ABCD为矩形的是( )
A.∠A+∠B=90° B.AB//CD,AB=CD,AC=BD C.AB//CD,AD=BC,AC=BD D.AC=BD,∠A=90°
3.矩形的一条边和一条对角线的夹角是40°,则两条对角线所夹的锐角等于( )
A.50° B.60 C.70° D.80°
二、填空题
4.矩形的面积为12cm ,一条边长为3cm,则矩形的对角线长为______.
5.如图,矩形ABCD中点E F分别是AB,CD的中点,连接DE和BF,分别取DE,BF的中点MN连接AM、CN、MN,若AB=2,BC=2,则图中阴影部分的面积为________.
6.如图,点O是菱形ABCD对角线的交点,DE//AC,CE//BD,连接OE,设AC=12 BD=16,则OE的长为________.
三、解答题
7.如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD.连接AC、CE、EF、AF.
(1)求证:四边形ACEF是矩形; (2)求四边形ACEF的周长.
8.如图,四边形ABCD中,对角线ACBD相交于点0,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形;
(2)若DE⊥AC交BC于E,∠ADB:∠CDB=2:3.则∠BDE的度数是多少
B组能力提升
一、填空题
9.如图,矩形OABC的顶点A.C 分别在坐标轴上B(8,7) D(5,0),点P是边AB或边BC上的一点,连接OP,DP,当△ODP为等腰三角形时,点P的坐标为________.
10.如图,在矩形ABCD中,E,F分别是边AB、AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=6,则GH的最小值是_______.
二、解答题
11.如图,在RtΔABC中,∠ACB=90°D是线段AB上一点,DE//BC,DF//AC,连接EF.CD.
(1)求证:EF=CD
(2)当D在线段AB的_______位置时,S矩形DECF =S△ABC.
(3)当CD与AB满足什么条件时,EF最短
C组拓展创新
解答题
12.如图1.已知AD//BC,AB//DC,∠B=∠C.
(1)求证:四边形ABCD为矩形;
(2)如图2,M为AD的中点,在AB上取一点N,使∠BNC=2∠DCM.
(i)若N为AB中点,BN=2,求CN的长;
(ii)若CM=3,CN=4,求BC的长.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
