2023-2024学年北师大版九年级数学上册1.3 正方形的性质与判定 同步练习题 (含2课时,无答案)
文档属性
| 名称 | 2023-2024学年北师大版九年级数学上册1.3 正方形的性质与判定 同步练习题 (含2课时,无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 164.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 16:10:43 | ||
图片预览

文档简介
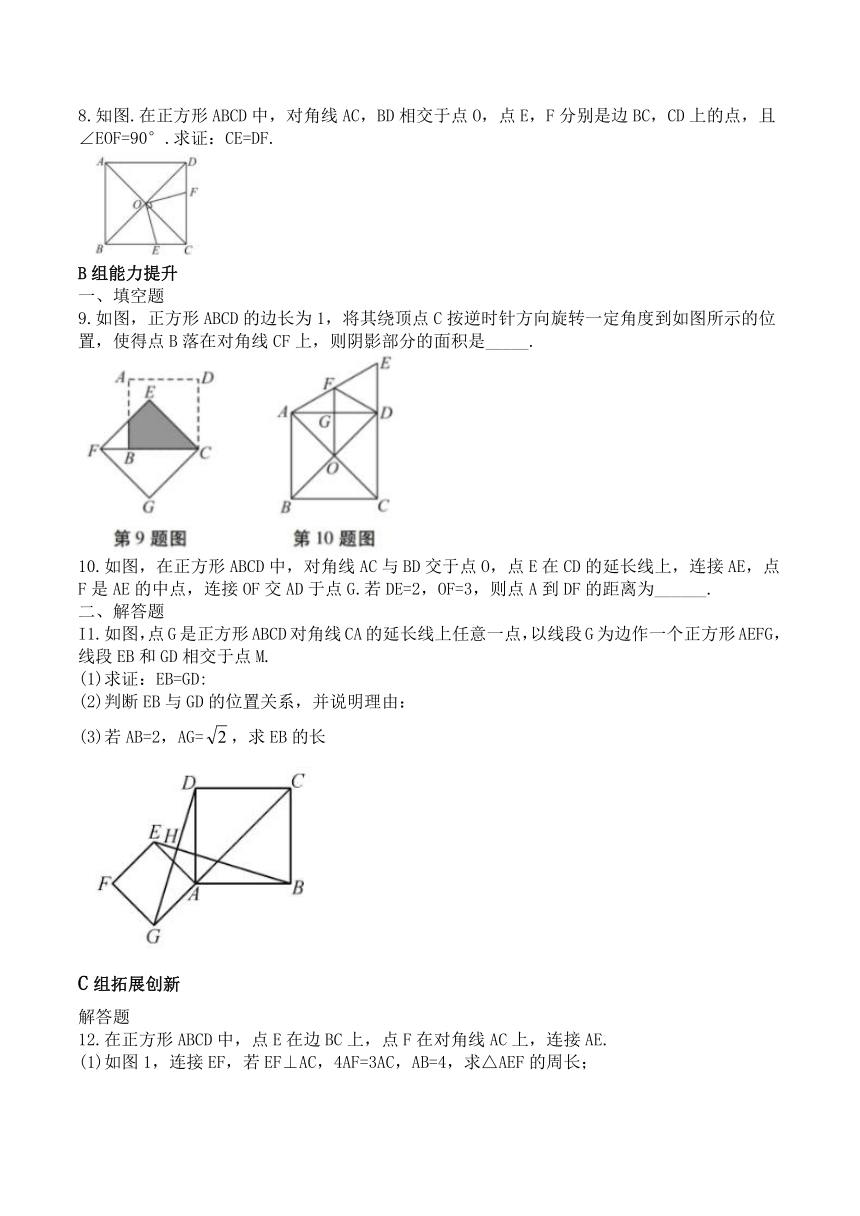
1.3 正方形的性质与判定 同步练习题 2023-2024学年北师大版九年级数学上册
第1课时 正方形的性质与判定(1)
A组基础过关
一、选择题
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等 C.对角线互相平分 D.对角相等
2.若正方形的周长为12,则这个正方形的对角线长为( )
A.6 B.3 C.2 D.3
3.如图,正方形ABCD的面积为2,菱形AECF的面积为1,则EF的长为( )
A.1 B.2 C. D.
二、填空题
4.若正方形的一条对角线为10,则这个正方形的而积为____.
5.边长为1的正方形的一个顶点到其他三个顶点的距离之和是______.
6.如图,正方形ABOC的边长为2,边0B与x轴负半轴的夹角为30°,则点C的坐标是____.
三、解答题
7.如图,在正方形ABCD中,点E、F分别是AB.BC上的点,且AE=BF,AF与E交于点G.求证:AF⊥DE.
8.知图.在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.求证:CE=DF.
B组能力提升
一、填空题
9.如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到如图所示的位置,使得点B落在对角线CF上,则阴影部分的面积是_____.
10.如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为______.
二、解答题
I1.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段G为边作一个正方形AEFG,线段EB和GD相交于点M.
(1)求证:EB=GD:
(2)判断EB与GD的位置关系,并说明理由:
(3)若AB=2,AG=,求EB的长
C组拓展创新
解答题
12.在正方形ABCD中,点E在边BC上,点F在对角线AC上,连接AE.
(1)如图1,连接EF,若EF⊥AC,4AF=3AC,AB=4,求△AEF的周长;
(2)如图2,若AF=AB,过点F作FG⊥AC交CD于G,点H在线段FG上(不与端点重合),连接AH.若∠EAH=45°,求证:EC=HG+FC.
第2课时 正方形的性质与判定(2)
A组基础过关
一、选择题
1.下列条件不能够判定“矩形ABCD是正方形”的是( )
A.AB=BC B.AC⊥BD C.AD=CD D.AC=BD
2.添加下列哪个条件,可证明菱形ABCD是正方形( )
A.AC=BD B.AB=CD C.BC=CD D.都不正确
3.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
二、填空题
4. ABCD的对线AC与BD相交于点O,且AC⊥BD,请添加一个条件______(答案不唯一),使得 ABCD为正方形.
5.如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,则EE′的长等于______.
6.以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_______.
三、解答题
7.如图,在△ABC中,在∠ACB=90°,CD平分∠ACB,DE⊥AC于E,DF⊥BC于F,求证:四边形CEDF是正方形.
8.如图,四边形ABCD的对角线AC,BD相交于点O,且OA=OB=OC=OD=1,AB=.四边形ABCD是正方形吗?说明理由.
B组能力提升
一、填空题
9.如图,在四边形ABCD中,∠ABC=∠CDA=90°,AB=BC,BE⊥AD于点E,四边形ABCD的面积为8,则BE等于_______.
10.如图,已知正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12...)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,...则顶点A2022的坐标为_______.
二、解答题
11.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF,∠BCE=∠DCF;
(2)若G在AD上,且∠GCE=45°,则GE=GF成立吗?为什么?
(3)在(2)的条件下,已知AE=4,AG=3,求正方形ABCD的面积.
C组拓展创新
解答题
12.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小,不用说明理由.
②当M点在何处时,AM+BM+CM的值最小,并说明理由.
(3)当AM+BM+CM的最小值为+1时,求正方形的边长.
第1课时 正方形的性质与判定(1)
A组基础过关
一、选择题
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等 C.对角线互相平分 D.对角相等
2.若正方形的周长为12,则这个正方形的对角线长为( )
A.6 B.3 C.2 D.3
3.如图,正方形ABCD的面积为2,菱形AECF的面积为1,则EF的长为( )
A.1 B.2 C. D.
二、填空题
4.若正方形的一条对角线为10,则这个正方形的而积为____.
5.边长为1的正方形的一个顶点到其他三个顶点的距离之和是______.
6.如图,正方形ABOC的边长为2,边0B与x轴负半轴的夹角为30°,则点C的坐标是____.
三、解答题
7.如图,在正方形ABCD中,点E、F分别是AB.BC上的点,且AE=BF,AF与E交于点G.求证:AF⊥DE.
8.知图.在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.求证:CE=DF.
B组能力提升
一、填空题
9.如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到如图所示的位置,使得点B落在对角线CF上,则阴影部分的面积是_____.
10.如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为______.
二、解答题
I1.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段G为边作一个正方形AEFG,线段EB和GD相交于点M.
(1)求证:EB=GD:
(2)判断EB与GD的位置关系,并说明理由:
(3)若AB=2,AG=,求EB的长
C组拓展创新
解答题
12.在正方形ABCD中,点E在边BC上,点F在对角线AC上,连接AE.
(1)如图1,连接EF,若EF⊥AC,4AF=3AC,AB=4,求△AEF的周长;
(2)如图2,若AF=AB,过点F作FG⊥AC交CD于G,点H在线段FG上(不与端点重合),连接AH.若∠EAH=45°,求证:EC=HG+FC.
第2课时 正方形的性质与判定(2)
A组基础过关
一、选择题
1.下列条件不能够判定“矩形ABCD是正方形”的是( )
A.AB=BC B.AC⊥BD C.AD=CD D.AC=BD
2.添加下列哪个条件,可证明菱形ABCD是正方形( )
A.AC=BD B.AB=CD C.BC=CD D.都不正确
3.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
二、填空题
4. ABCD的对线AC与BD相交于点O,且AC⊥BD,请添加一个条件______(答案不唯一),使得 ABCD为正方形.
5.如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,则EE′的长等于______.
6.以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_______.
三、解答题
7.如图,在△ABC中,在∠ACB=90°,CD平分∠ACB,DE⊥AC于E,DF⊥BC于F,求证:四边形CEDF是正方形.
8.如图,四边形ABCD的对角线AC,BD相交于点O,且OA=OB=OC=OD=1,AB=.四边形ABCD是正方形吗?说明理由.
B组能力提升
一、填空题
9.如图,在四边形ABCD中,∠ABC=∠CDA=90°,AB=BC,BE⊥AD于点E,四边形ABCD的面积为8,则BE等于_______.
10.如图,已知正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12...)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,...则顶点A2022的坐标为_______.
二、解答题
11.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF,∠BCE=∠DCF;
(2)若G在AD上,且∠GCE=45°,则GE=GF成立吗?为什么?
(3)在(2)的条件下,已知AE=4,AG=3,求正方形ABCD的面积.
C组拓展创新
解答题
12.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小,不用说明理由.
②当M点在何处时,AM+BM+CM的值最小,并说明理由.
(3)当AM+BM+CM的最小值为+1时,求正方形的边长.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
