2.5有理数的加法与减法 提优练习(无答案) 2023-2024学年苏科版七年级数学上册
文档属性
| 名称 | 2.5有理数的加法与减法 提优练习(无答案) 2023-2024学年苏科版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 122.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 17:12:23 | ||
图片预览

文档简介
2.5有理数的加法与减法 (提优练习)
选择题(本题共10小题)
1.下列计算正确的是( )
A.(+6)+(-13)=+7 B.(+6)+(-13)=-19
C.(+6)+(-13)=-7 D.(-5)+(-3)=8
2.某天上午6时某河流水位为80.4米,到上午12时水位上涨了5.3米,到下午6时水位下跌了0.9米.到下午6时水位为( )米.
A.76 B.84.8 C.85.8 D.86.6
3.在有理数2,0,﹣1,﹣3中,任意取两个数相加,和最小是( )
A.2 B.﹣1 C.﹣3 D.﹣4
4.已知|a|=5,|b|=2,且a<0,b>0,则a+b的值为( )
A.7 B.﹣7 C.3 D.﹣3
5.下面结论正确的有 ( )
①0是最小的整数;②在数轴上7与9之间的有理数只有8;③若a+b=0,则a、b互为相反数; ④有理数相减,差不一定小于被减数;⑤1是绝对值最小的正数; ⑥有理数分为正有理数和负有理数.
A.1个 B.2个 C.3个 D.4个
6.若一组数据2,4,7,x中,最大的数与最小的数的差是8,则x的值是( )
A.-1 B.10 C.-1或10 D.无法确定
7.在计算时,佳佳的板演过程如下:
解:原式.
老师问:“佳佳同学在解答过程中运用了哪些运算律?”
甲同学回答说:“佳佳在解答过程中运用了加法交换律”;
乙同学回答说:“佳佳在解答过程中运用了加法结合律”;
丙同学回答说:“佳佳在解答过程中既运用了加法交换律,也运用了加法结合律”.
下列对甲、乙、丙三名同学说法判断正确的是( )
A.甲同学说的对 B.乙同学说的对
C.丙同学说的对 D.甲、乙、丙说的都不对
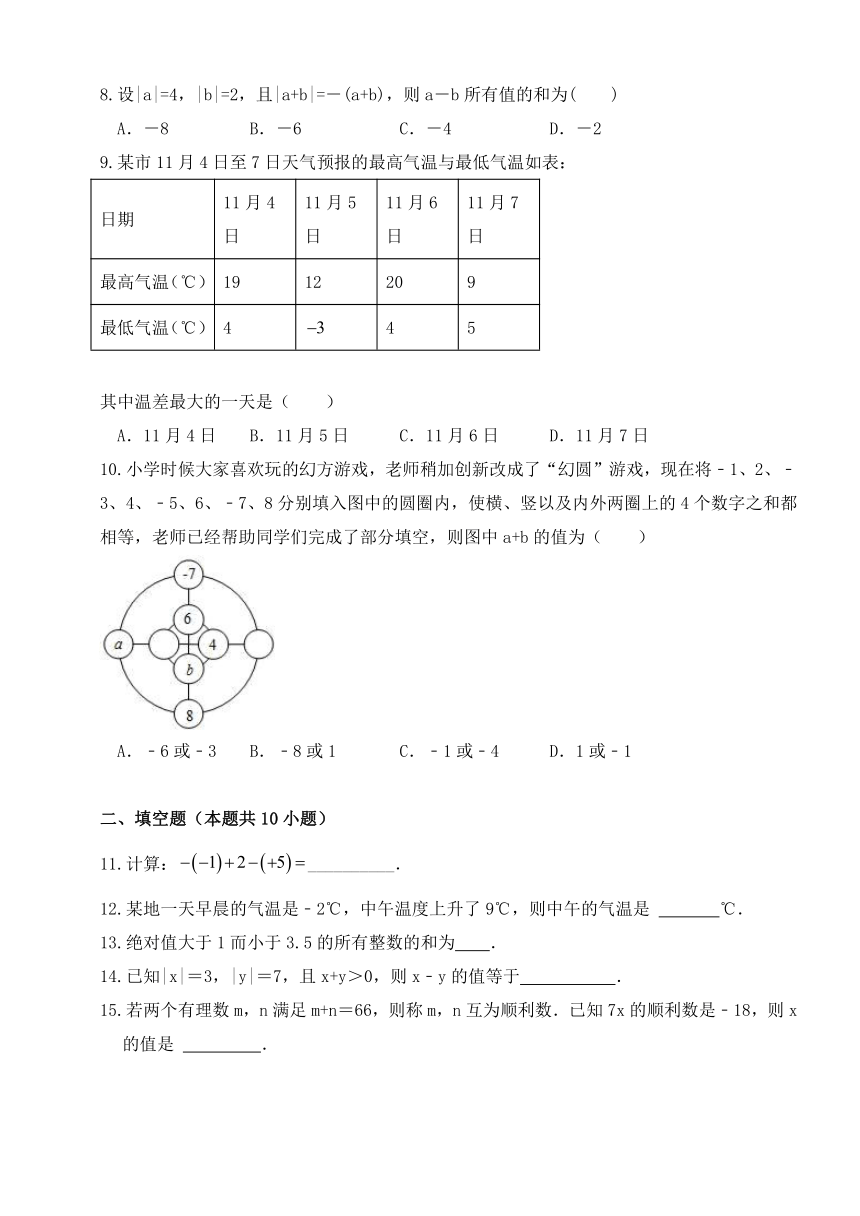
8.设|a|=4,|b|=2,且|a+b|=-(a+b),则a-b所有值的和为( )
A.-8 B.-6 C.-4 D.-2
9.某市11月4日至7日天气预报的最高气温与最低气温如表:
日期 11月4日 11月5日 11月6日 11月7日
最高气温(℃) 19 12 20 9
最低气温(℃) 4 4 5
其中温差最大的一天是( )
A.11月4日 B.11月5日 C.11月6日 D.11月7日
10.小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )
A.﹣6或﹣3 B.﹣8或1 C.﹣1或﹣4 D.1或﹣1
填空题(本题共10小题)
11.计算:__________.
12.某地一天早晨的气温是﹣2℃,中午温度上升了9℃,则中午的气温是 ℃.
13.绝对值大于1而小于3.5的所有整数的和为 .
14.已知|x|=3,|y|=7,且x+y>0,则x﹣y的值等于 .
15.若两个有理数m,n满足m+n=66,则称m,n互为顺利数.已知7x的顺利数是﹣18,则x的值是 .
16.规定一种新运算“☆”对于任意两个有理数a和b,有a☆b=a-b+1,请你根据新运算,计算(2☆3)☆2的值是___________
17.已知x,a,b为互不相等的三个有理数,且a>b,若式子|x﹣a|+|x﹣b|的最小值为2,则2022+a﹣b的值为 .
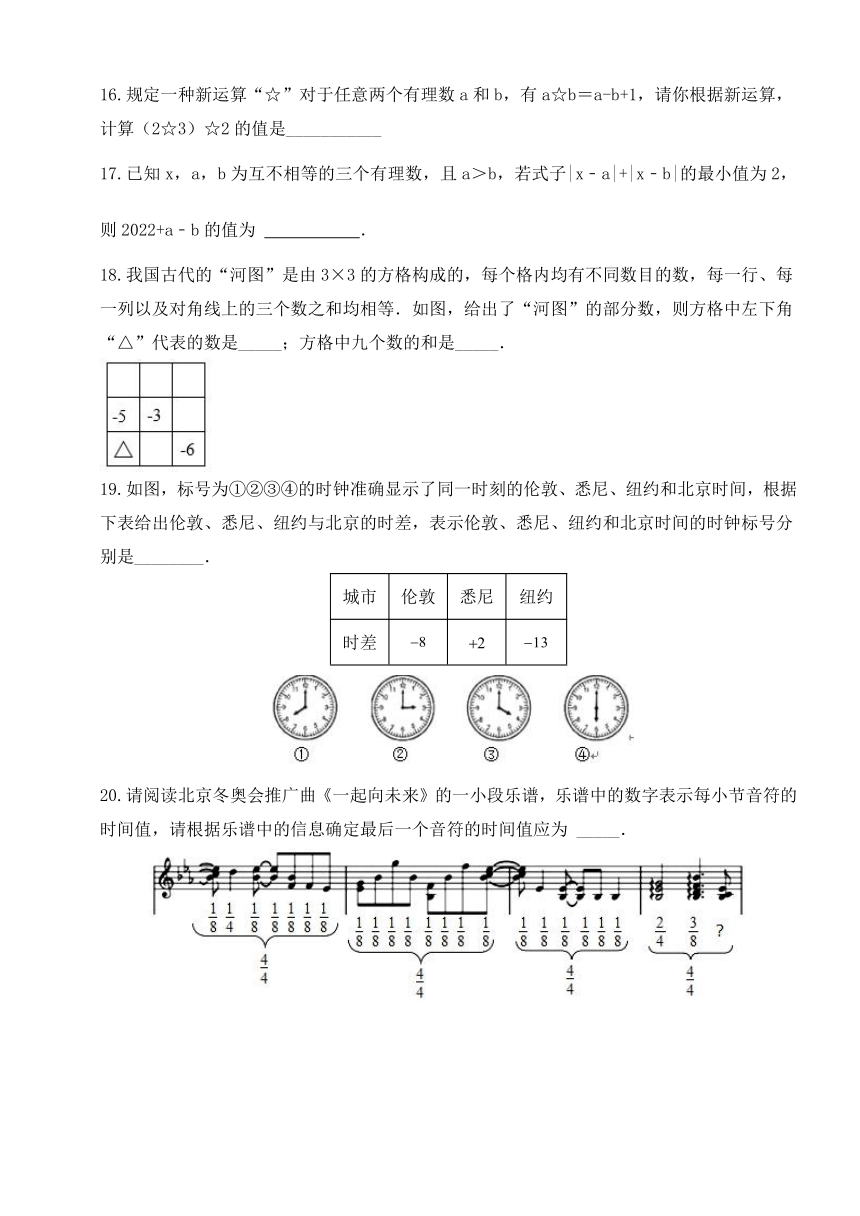
18.我国古代的“河图”是由3×3的方格构成的,每个格内均有不同数目的数,每一行、每一列以及对角线上的三个数之和均相等.如图,给出了“河图”的部分数,则方格中左下角“△”代表的数是_____;方格中九个数的和是_____.
19.如图,标号为①②③④的时钟准确显示了同一时刻的伦敦、悉尼、纽约和北京时间,根据下表给出伦敦、悉尼、纽约与北京的时差,表示伦敦、悉尼、纽约和北京时间的时钟标号分别是________.
城市 伦敦 悉尼 纽约
时差
20.请阅读北京冬奥会推广曲《一起向未来》的一小段乐谱,乐谱中的数字表示每小节音符的时间值,请根据乐谱中的信息确定最后一个音符的时间值应为 _____.
解答题(本题共7小题)
21.计算:
(1)(﹣23)+(+58)+(﹣17) (2)(﹣2.8)+(﹣3.6)+(﹣1.5)+3.6
(3)﹣27+(﹣32)+(﹣8)+72 (4)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4)
(5) (6)
22.已知,,,且,,求的值.
23.“双减”政策实施后,同学们作业负担大大减少,小明记录了本周写家庭作业的时间,情况如下表(以30分钟为标准,时间多于30分钟用正数表示,时间少于30分钟用负数表示):
星期 一 二 三 四 五 六 日
与标准时间的差(分钟) -5 -6 -8 -2 -9 +8 +15
(1)这一周内写家庭作业用时最多的是星期_________,用时最少的是星期_____________;
(2)求小明这一周每天写家庭作业的平均时间.
24.一名足球守门员练习折返跑,从球门线出发,向前记为正数,返回记为负数,他的记录如下(单位:米):+5,﹣3,+10,﹣8,﹣6,+12,﹣10,
(1)守门员最后是否回到了球门线的位置?
(2)守门员全部练习结束后,共跑了多少米?
(3)在练习过程中,守门员离开球门线的最远距离是多少米?
25.水库管理人员为了掌握水库蓄水情况,需要观测水库的水位变化,下表是某水库一星期内的水位高低的变化情况(水位比前一天上升记为正数,下降计为负数),已知上周日水库的水位为20米.
星期 一 二 三 四 五 六 日
水位变化/米 +0.2 -0.1 -0.3 -0.2 -0.1 -0.2 +0.3
(1)与上周日相比,本周日的水位是上升了还是下降了?上升(或下降)了多少米?
(2)完成上面本周的水位记录表:
星期 一 二 三 四 五 六 日
水位变化/米
(3)本周内哪天水位最高?哪天的水位最低,它们相差多少?
26.2022年11月20日18:00(北京时间),卡塔尔世界杯开幕式在豪尔市的海湾球场举行.小明为 方便各国球迷准时观看比赛,列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数).
城市 纽约 东京 豪尔市
时差/时
假设现在北京时间是2020年11月22日上午9:00.
(1)现在纽约的时间是几点?东京时间是几点?
(2)如果小明在北京坐11月19日上午10:00的航班飞行约9小时到达豪尔市,那么达到豪尔市的时间是几点?
27.如图是三个三角形,每个三角形的顶点处都有一个“〇”,在每个“〇”中填入一个数,满足这三个三角形的3个顶点处的“〇”中的数的和都等于2.
(1)将﹣8、﹣7、﹣6、﹣4、1、3、5、9、13这9个数填入恰当的位置,使得这三个三角形的3个顶点处的“〇”中的数的和都等于2;
(2)如果将(1)中的这9个数改为﹣13、﹣9、﹣5、﹣3、﹣1、4、6、7、8,还能满足要求吗?如果满足,请填在“〇”中;如果不满足,请说明理由.
选择题(本题共10小题)
1.下列计算正确的是( )
A.(+6)+(-13)=+7 B.(+6)+(-13)=-19
C.(+6)+(-13)=-7 D.(-5)+(-3)=8
2.某天上午6时某河流水位为80.4米,到上午12时水位上涨了5.3米,到下午6时水位下跌了0.9米.到下午6时水位为( )米.
A.76 B.84.8 C.85.8 D.86.6
3.在有理数2,0,﹣1,﹣3中,任意取两个数相加,和最小是( )
A.2 B.﹣1 C.﹣3 D.﹣4
4.已知|a|=5,|b|=2,且a<0,b>0,则a+b的值为( )
A.7 B.﹣7 C.3 D.﹣3
5.下面结论正确的有 ( )
①0是最小的整数;②在数轴上7与9之间的有理数只有8;③若a+b=0,则a、b互为相反数; ④有理数相减,差不一定小于被减数;⑤1是绝对值最小的正数; ⑥有理数分为正有理数和负有理数.
A.1个 B.2个 C.3个 D.4个
6.若一组数据2,4,7,x中,最大的数与最小的数的差是8,则x的值是( )
A.-1 B.10 C.-1或10 D.无法确定
7.在计算时,佳佳的板演过程如下:
解:原式.
老师问:“佳佳同学在解答过程中运用了哪些运算律?”
甲同学回答说:“佳佳在解答过程中运用了加法交换律”;
乙同学回答说:“佳佳在解答过程中运用了加法结合律”;
丙同学回答说:“佳佳在解答过程中既运用了加法交换律,也运用了加法结合律”.
下列对甲、乙、丙三名同学说法判断正确的是( )
A.甲同学说的对 B.乙同学说的对
C.丙同学说的对 D.甲、乙、丙说的都不对
8.设|a|=4,|b|=2,且|a+b|=-(a+b),则a-b所有值的和为( )
A.-8 B.-6 C.-4 D.-2
9.某市11月4日至7日天气预报的最高气温与最低气温如表:
日期 11月4日 11月5日 11月6日 11月7日
最高气温(℃) 19 12 20 9
最低气温(℃) 4 4 5
其中温差最大的一天是( )
A.11月4日 B.11月5日 C.11月6日 D.11月7日
10.小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )
A.﹣6或﹣3 B.﹣8或1 C.﹣1或﹣4 D.1或﹣1
填空题(本题共10小题)
11.计算:__________.
12.某地一天早晨的气温是﹣2℃,中午温度上升了9℃,则中午的气温是 ℃.
13.绝对值大于1而小于3.5的所有整数的和为 .
14.已知|x|=3,|y|=7,且x+y>0,则x﹣y的值等于 .
15.若两个有理数m,n满足m+n=66,则称m,n互为顺利数.已知7x的顺利数是﹣18,则x的值是 .
16.规定一种新运算“☆”对于任意两个有理数a和b,有a☆b=a-b+1,请你根据新运算,计算(2☆3)☆2的值是___________
17.已知x,a,b为互不相等的三个有理数,且a>b,若式子|x﹣a|+|x﹣b|的最小值为2,则2022+a﹣b的值为 .
18.我国古代的“河图”是由3×3的方格构成的,每个格内均有不同数目的数,每一行、每一列以及对角线上的三个数之和均相等.如图,给出了“河图”的部分数,则方格中左下角“△”代表的数是_____;方格中九个数的和是_____.
19.如图,标号为①②③④的时钟准确显示了同一时刻的伦敦、悉尼、纽约和北京时间,根据下表给出伦敦、悉尼、纽约与北京的时差,表示伦敦、悉尼、纽约和北京时间的时钟标号分别是________.
城市 伦敦 悉尼 纽约
时差
20.请阅读北京冬奥会推广曲《一起向未来》的一小段乐谱,乐谱中的数字表示每小节音符的时间值,请根据乐谱中的信息确定最后一个音符的时间值应为 _____.
解答题(本题共7小题)
21.计算:
(1)(﹣23)+(+58)+(﹣17) (2)(﹣2.8)+(﹣3.6)+(﹣1.5)+3.6
(3)﹣27+(﹣32)+(﹣8)+72 (4)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4)
(5) (6)
22.已知,,,且,,求的值.
23.“双减”政策实施后,同学们作业负担大大减少,小明记录了本周写家庭作业的时间,情况如下表(以30分钟为标准,时间多于30分钟用正数表示,时间少于30分钟用负数表示):
星期 一 二 三 四 五 六 日
与标准时间的差(分钟) -5 -6 -8 -2 -9 +8 +15
(1)这一周内写家庭作业用时最多的是星期_________,用时最少的是星期_____________;
(2)求小明这一周每天写家庭作业的平均时间.
24.一名足球守门员练习折返跑,从球门线出发,向前记为正数,返回记为负数,他的记录如下(单位:米):+5,﹣3,+10,﹣8,﹣6,+12,﹣10,
(1)守门员最后是否回到了球门线的位置?
(2)守门员全部练习结束后,共跑了多少米?
(3)在练习过程中,守门员离开球门线的最远距离是多少米?
25.水库管理人员为了掌握水库蓄水情况,需要观测水库的水位变化,下表是某水库一星期内的水位高低的变化情况(水位比前一天上升记为正数,下降计为负数),已知上周日水库的水位为20米.
星期 一 二 三 四 五 六 日
水位变化/米 +0.2 -0.1 -0.3 -0.2 -0.1 -0.2 +0.3
(1)与上周日相比,本周日的水位是上升了还是下降了?上升(或下降)了多少米?
(2)完成上面本周的水位记录表:
星期 一 二 三 四 五 六 日
水位变化/米
(3)本周内哪天水位最高?哪天的水位最低,它们相差多少?
26.2022年11月20日18:00(北京时间),卡塔尔世界杯开幕式在豪尔市的海湾球场举行.小明为 方便各国球迷准时观看比赛,列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数).
城市 纽约 东京 豪尔市
时差/时
假设现在北京时间是2020年11月22日上午9:00.
(1)现在纽约的时间是几点?东京时间是几点?
(2)如果小明在北京坐11月19日上午10:00的航班飞行约9小时到达豪尔市,那么达到豪尔市的时间是几点?
27.如图是三个三角形,每个三角形的顶点处都有一个“〇”,在每个“〇”中填入一个数,满足这三个三角形的3个顶点处的“〇”中的数的和都等于2.
(1)将﹣8、﹣7、﹣6、﹣4、1、3、5、9、13这9个数填入恰当的位置,使得这三个三角形的3个顶点处的“〇”中的数的和都等于2;
(2)如果将(1)中的这9个数改为﹣13、﹣9、﹣5、﹣3、﹣1、4、6、7、8,还能满足要求吗?如果满足,请填在“〇”中;如果不满足,请说明理由.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
