2023-2024学年 人教版八年级数学上册11.3多边形及其内角和提高训练 (含答案)
文档属性
| 名称 | 2023-2024学年 人教版八年级数学上册11.3多边形及其内角和提高训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 194.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 18:09:49 | ||
图片预览

文档简介
多边形及其内角和
一、单选题
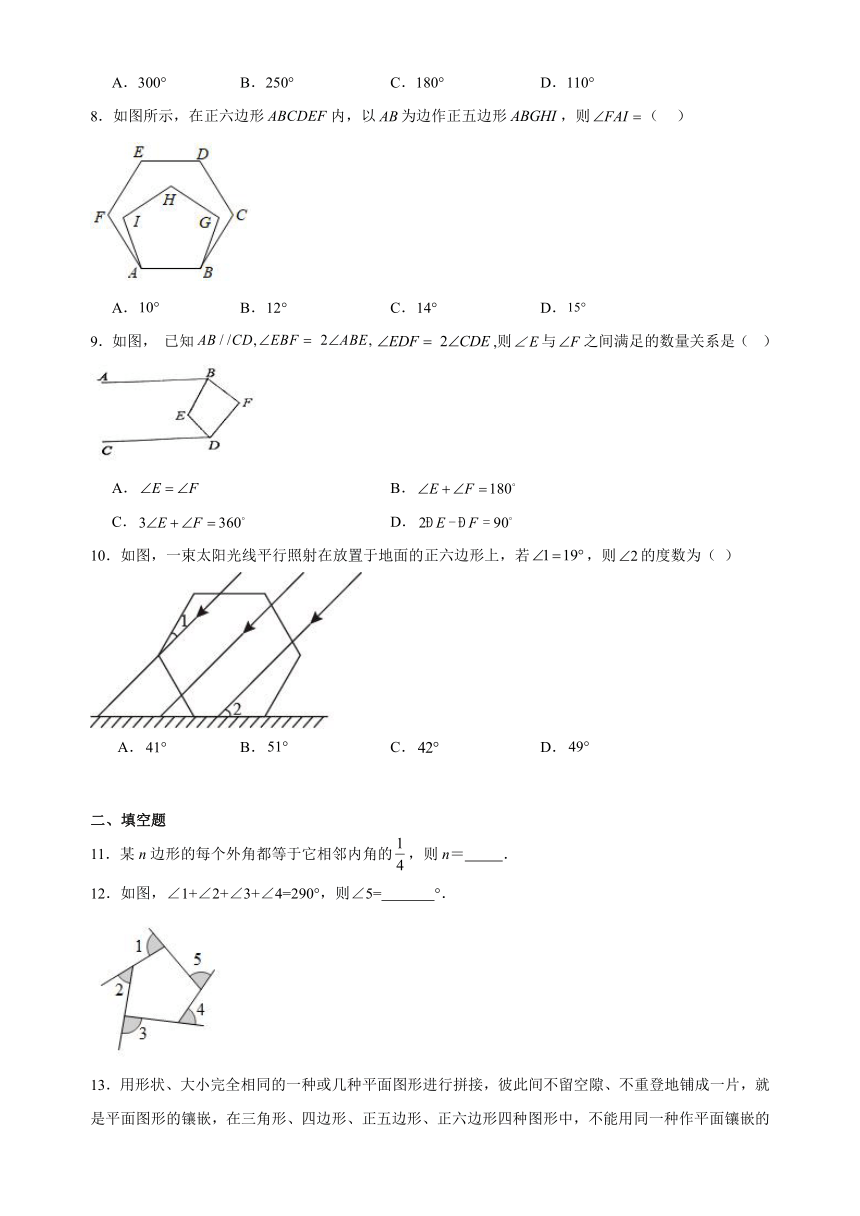
1.若一个多边形的内角和是,则该多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
2.一个多边形的内角和比它的外角和的4倍少180°,这个多边形的边数是( )
A.6 B.7 C.8 D.9
3.如图,一张含有80°的三角形纸片,剪去这个80°角后,得到一个四边形,则∠1+∠2的度数是( )
A.200° B.240° C.260° D.300°
4.一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为( )
A.8 B.9 C.10 D.12
5.如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
6.如图所示,在四边形中,,,它的一个外角,则的大小是( )
A.70° B.60° C.40° D.30°
7.如图,在中,,若沿图中虚线截去,则等于( ).
A.300° B.250° C.180° D.110°
8.如图所示,在正六边形内,以为边作正五边形,则( )
A. B. C. D.
9.如图, 已知,则与之间满足的数量关系是( )
A. B.
C. D.
10.如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
二、填空题
11.某n边形的每个外角都等于它相邻内角的,则n= .
12.如图,∠1+∠2+∠3+∠4=290°,则∠5= °.
13.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此间不留空隙、不重登地铺成一片,就是平面图形的镶嵌,在三角形、四边形、正五边形、正六边形四种图形中,不能用同一种作平面镶嵌的图形是 .
14.若一个多边形的每个外角都是40°,则从这个多边形的一个顶点出发可以画 条对角线.
15.将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=30°,那么∠1+∠2= °.
16.如图,在五边形中,∠A+∠B+∠C=310o,分别平分∠EDC,∠BCD,则∠CPD的度数是 .
三、解答题
17.填表:
多边形的边数 3 4 5 6 8 12
内角和
外角和
18.如图所示,在△ABC中,高AD,BE相交于点H,且∠CAB比∠ABC大10°,∠ABC比∠C大10°,求∠EHD的度数.
19.在四边形中,∠B=∠D=90o,,分别平分∠BAD和∠BCD.
(1)若∠EAB=32o,求∠FCE的度数.
(2)证明:AE//CF.
20.课本上介绍了求多边形的内角和的方法:过边形的一个顶点作对角线,把边形分成个三角形,把求多边形的问题转化成三角形内角和的问题,从而得到边形的内角和等于.现在再提供一种添辅助线的方案,请将方案补充完整,并说明“边形的内角和等于”.
(注:此为时的示意图,说明问题时注意多边形为n边形)
如图,P为n边形.内边上的任意一点(不与点,重合),连接,,…,,那么n边形被分成了( )个三角形,由此推理n边形的内角和定理.
参考答案:
1.C
2.D
3.C
4.C
5.C
6.C
7.B
8.B
9.C
10.A
11.10.
12.
13.正五边形
14.6
15.72
16./65度
18.∠EHD=130°.
19.
20.
一、单选题
1.若一个多边形的内角和是,则该多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
2.一个多边形的内角和比它的外角和的4倍少180°,这个多边形的边数是( )
A.6 B.7 C.8 D.9
3.如图,一张含有80°的三角形纸片,剪去这个80°角后,得到一个四边形,则∠1+∠2的度数是( )
A.200° B.240° C.260° D.300°
4.一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为( )
A.8 B.9 C.10 D.12
5.如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
6.如图所示,在四边形中,,,它的一个外角,则的大小是( )
A.70° B.60° C.40° D.30°
7.如图,在中,,若沿图中虚线截去,则等于( ).
A.300° B.250° C.180° D.110°
8.如图所示,在正六边形内,以为边作正五边形,则( )
A. B. C. D.
9.如图, 已知,则与之间满足的数量关系是( )
A. B.
C. D.
10.如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
二、填空题
11.某n边形的每个外角都等于它相邻内角的,则n= .
12.如图,∠1+∠2+∠3+∠4=290°,则∠5= °.
13.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此间不留空隙、不重登地铺成一片,就是平面图形的镶嵌,在三角形、四边形、正五边形、正六边形四种图形中,不能用同一种作平面镶嵌的图形是 .
14.若一个多边形的每个外角都是40°,则从这个多边形的一个顶点出发可以画 条对角线.
15.将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=30°,那么∠1+∠2= °.
16.如图,在五边形中,∠A+∠B+∠C=310o,分别平分∠EDC,∠BCD,则∠CPD的度数是 .
三、解答题
17.填表:
多边形的边数 3 4 5 6 8 12
内角和
外角和
18.如图所示,在△ABC中,高AD,BE相交于点H,且∠CAB比∠ABC大10°,∠ABC比∠C大10°,求∠EHD的度数.
19.在四边形中,∠B=∠D=90o,,分别平分∠BAD和∠BCD.
(1)若∠EAB=32o,求∠FCE的度数.
(2)证明:AE//CF.
20.课本上介绍了求多边形的内角和的方法:过边形的一个顶点作对角线,把边形分成个三角形,把求多边形的问题转化成三角形内角和的问题,从而得到边形的内角和等于.现在再提供一种添辅助线的方案,请将方案补充完整,并说明“边形的内角和等于”.
(注:此为时的示意图,说明问题时注意多边形为n边形)
如图,P为n边形.内边上的任意一点(不与点,重合),连接,,…,,那么n边形被分成了( )个三角形,由此推理n边形的内角和定理.
参考答案:
1.C
2.D
3.C
4.C
5.C
6.C
7.B
8.B
9.C
10.A
11.10.
12.
13.正五边形
14.6
15.72
16./65度
18.∠EHD=130°.
19.
20.
