2023-2024学年京改版八年级数学上册 12.2 三角形的性质( 第3课时 )教学设计 (表格式)
文档属性
| 名称 | 2023-2024学年京改版八年级数学上册 12.2 三角形的性质( 第3课时 )教学设计 (表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 00:00:00 | ||
图片预览

文档简介
课程基本信息
课题 三角形的性质(3)
教学目标
教学目标: 1. 理解三角形外角的定义,并能够准确的在图形中找出三角形的外角。能说出三角形外角性质的内容;能够用三角形外角的性质进行三角形及相关图形中角的计算,逐步培养和发展学生的逻辑思维能力和推理论证表达能力。 2.借助图形思考证明三角形外角性质的过程,发展学生的空间观念,通过应用尝试从不同角度寻求分析问题和解决问题的方法,体验解决问题方法的多样性。 3.通过对三角形外角证明及应用,体会感受数学的严谨性,培养主动探索,勇于发表自己的观点,敢于实践的精神和良好的合作交流的学习习惯。 教学重点:在图形中三角形外角的识别。 教学难点:外角性质的探究及应用。
教学过程
时间 教学环节 主要师生活动
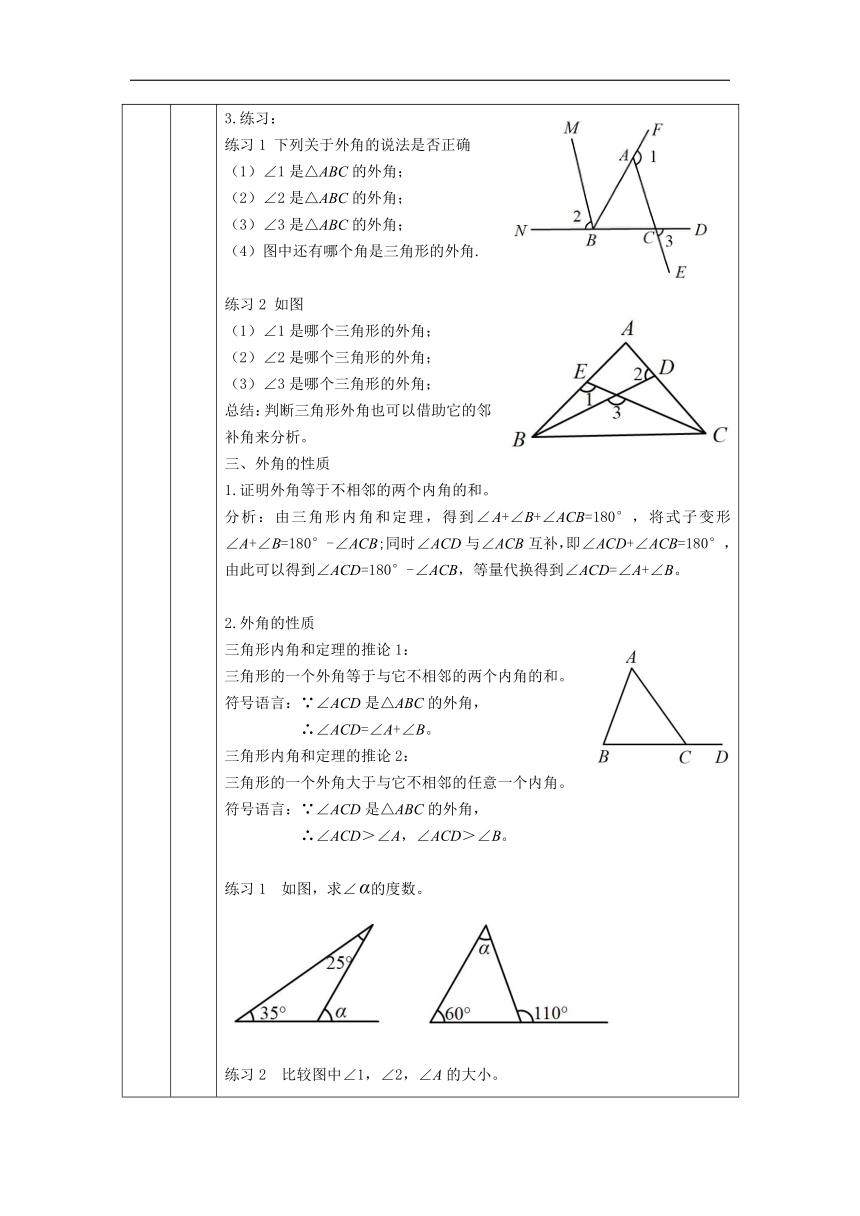
20分钟 一、复习回顾 二、 探究新知 三、 例题讲解 四、课堂总结 五、 作业 三角形角的性质: 三角形三个内角的和等于180°。 二、外角的定义 1.外角的定义: 如图,点D是△ABC的边BC延长线上的一点,那么∠ACD叫做△ABC的一个外角。 特点: 活动一:作△ABC的外角; 活动二:总结外角的特点。 ①三角形的外角是三角形的一边与另一边的延长线的夹角。 ②三角形的外角是相邻内角的邻补角。 练习: 练习1 下列关于外角的说法是否正确 ∠1是△ABC的外角; ∠2是△ABC的外角; ∠3是△ABC的外角; 图中还有哪个角是三角形的外角. 练习2 如图 (1)∠1是哪个三角形的外角; (2)∠2是哪个三角形的外角; (3)∠3是哪个三角形的外角; 总结:判断三角形外角也可以借助它的邻补角来分析。 外角的性质 1.证明外角等于不相邻的两个内角的和。 分析:由三角形内角和定理,得到∠A+∠B+∠ACB=180°,将式子变形∠A+∠B=180°-∠ACB;同时∠ACD与∠ACB互补,即∠ACD+∠ACB=180°,由此可以得到∠ACD=180°-∠ACB,等量代换得到∠ACD=∠A+∠B。 2.外角的性质 三角形内角和定理的推论1: 三角形的一个外角等于与它不相邻的两个内角的和。 符号语言:∵∠ACD是△ABC的外角, ∴∠ACD=∠A+∠B。 三角形内角和定理的推论2: 三角形的一个外角大于与它不相邻的任意一个内角。 符号语言:∵∠ACD是△ABC的外角, ∴∠ACD>∠A,∠ACD>∠B。 练习1 如图,求∠的度数。 练习2 比较图中∠1,∠2,∠A的大小。 例题 例1点B,C,D,E是同一条直线上的四点,∠B=∠BAC=30°,∠CAD=60°,求∠ADE的度数。 思路一: ①∠ADE是△ACD外角:∠ADE=∠1+∠CAD; ②∠1是△ABC外角,∠1=∠B+∠BAC。 思路二: ∠ADE是△ABD的外角,∠ADE=∠B+∠BAD=∠B+∠BAC+∠CAD。 例2 如图,D是BC延长线上一点,E是CA 延长线上一点,F是AB延长线上一点, 求∠BAE +∠CBF +∠ACD等于多少度. 分析: 根据三角形内角和定理的推论1,△ABC的三个外角可以分别表示为不相邻的两个内角和, 即∠BAE=∠2+∠3, ∠CBF=∠1+∠3, ∠ACD=∠1+∠2。 求三个外角的和即把三个等式相加,结合三角形内角和定理,即可得出结论。 锐角三角形,直角三角形,钝角三角形 概念 思考:三角形的内角中最多能有几个钝角?最多能有几个直角?最多能有几个锐角? 我们把 三个角都是锐角的三角形叫做锐角三角形; 有一个角是直角的三角形叫做直角三角形; 有一个角是钝角的三角形叫做钝角三角形. 将三角形按角分类 三角形 直角三角形的一个判定方法: 有两个锐角互余的三角形是直角三角形. 符号语言:∵∠A+∠C=90°, ∴△ABC为直角三角形。 练习:在△ABC中,∠A=43°,∠B=47°,试判断三角形的形状。 答:△ABC是直角三角形。 课堂小结: 通过本节课的学习,你有什么体会和收获? 1、 外角 三角形按角大小分类 锐角三角形 直角三角形 钝角三角形 3.直角三角形的一个判定方法: 有两个锐角互余的三角形是直角三角形。 作业: 已知:如图,D是BA延长线上一点,E是CB延长线上一点, F是AC延 长线上一点,∠DAC=140°,∠ACB=100°,求∠ABE的度数。 如图所示的五角星中,∠A+∠B+∠C+∠D+∠E 等于多少度? 第一题 第二题
课题 三角形的性质(3)
教学目标
教学目标: 1. 理解三角形外角的定义,并能够准确的在图形中找出三角形的外角。能说出三角形外角性质的内容;能够用三角形外角的性质进行三角形及相关图形中角的计算,逐步培养和发展学生的逻辑思维能力和推理论证表达能力。 2.借助图形思考证明三角形外角性质的过程,发展学生的空间观念,通过应用尝试从不同角度寻求分析问题和解决问题的方法,体验解决问题方法的多样性。 3.通过对三角形外角证明及应用,体会感受数学的严谨性,培养主动探索,勇于发表自己的观点,敢于实践的精神和良好的合作交流的学习习惯。 教学重点:在图形中三角形外角的识别。 教学难点:外角性质的探究及应用。
教学过程
时间 教学环节 主要师生活动
20分钟 一、复习回顾 二、 探究新知 三、 例题讲解 四、课堂总结 五、 作业 三角形角的性质: 三角形三个内角的和等于180°。 二、外角的定义 1.外角的定义: 如图,点D是△ABC的边BC延长线上的一点,那么∠ACD叫做△ABC的一个外角。 特点: 活动一:作△ABC的外角; 活动二:总结外角的特点。 ①三角形的外角是三角形的一边与另一边的延长线的夹角。 ②三角形的外角是相邻内角的邻补角。 练习: 练习1 下列关于外角的说法是否正确 ∠1是△ABC的外角; ∠2是△ABC的外角; ∠3是△ABC的外角; 图中还有哪个角是三角形的外角. 练习2 如图 (1)∠1是哪个三角形的外角; (2)∠2是哪个三角形的外角; (3)∠3是哪个三角形的外角; 总结:判断三角形外角也可以借助它的邻补角来分析。 外角的性质 1.证明外角等于不相邻的两个内角的和。 分析:由三角形内角和定理,得到∠A+∠B+∠ACB=180°,将式子变形∠A+∠B=180°-∠ACB;同时∠ACD与∠ACB互补,即∠ACD+∠ACB=180°,由此可以得到∠ACD=180°-∠ACB,等量代换得到∠ACD=∠A+∠B。 2.外角的性质 三角形内角和定理的推论1: 三角形的一个外角等于与它不相邻的两个内角的和。 符号语言:∵∠ACD是△ABC的外角, ∴∠ACD=∠A+∠B。 三角形内角和定理的推论2: 三角形的一个外角大于与它不相邻的任意一个内角。 符号语言:∵∠ACD是△ABC的外角, ∴∠ACD>∠A,∠ACD>∠B。 练习1 如图,求∠的度数。 练习2 比较图中∠1,∠2,∠A的大小。 例题 例1点B,C,D,E是同一条直线上的四点,∠B=∠BAC=30°,∠CAD=60°,求∠ADE的度数。 思路一: ①∠ADE是△ACD外角:∠ADE=∠1+∠CAD; ②∠1是△ABC外角,∠1=∠B+∠BAC。 思路二: ∠ADE是△ABD的外角,∠ADE=∠B+∠BAD=∠B+∠BAC+∠CAD。 例2 如图,D是BC延长线上一点,E是CA 延长线上一点,F是AB延长线上一点, 求∠BAE +∠CBF +∠ACD等于多少度. 分析: 根据三角形内角和定理的推论1,△ABC的三个外角可以分别表示为不相邻的两个内角和, 即∠BAE=∠2+∠3, ∠CBF=∠1+∠3, ∠ACD=∠1+∠2。 求三个外角的和即把三个等式相加,结合三角形内角和定理,即可得出结论。 锐角三角形,直角三角形,钝角三角形 概念 思考:三角形的内角中最多能有几个钝角?最多能有几个直角?最多能有几个锐角? 我们把 三个角都是锐角的三角形叫做锐角三角形; 有一个角是直角的三角形叫做直角三角形; 有一个角是钝角的三角形叫做钝角三角形. 将三角形按角分类 三角形 直角三角形的一个判定方法: 有两个锐角互余的三角形是直角三角形. 符号语言:∵∠A+∠C=90°, ∴△ABC为直角三角形。 练习:在△ABC中,∠A=43°,∠B=47°,试判断三角形的形状。 答:△ABC是直角三角形。 课堂小结: 通过本节课的学习,你有什么体会和收获? 1、 外角 三角形按角大小分类 锐角三角形 直角三角形 钝角三角形 3.直角三角形的一个判定方法: 有两个锐角互余的三角形是直角三角形。 作业: 已知:如图,D是BA延长线上一点,E是CB延长线上一点, F是AC延 长线上一点,∠DAC=140°,∠ACB=100°,求∠ABE的度数。 如图所示的五角星中,∠A+∠B+∠C+∠D+∠E 等于多少度? 第一题 第二题
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
