11.2 与三角形有关的角 同步练习(含解析)2022-2023学年上学期广西各地八年级数学期末试题选编
文档属性
| 名称 | 11.2 与三角形有关的角 同步练习(含解析)2022-2023学年上学期广西各地八年级数学期末试题选编 |  | |
| 格式 | docx | ||
| 文件大小 | 707.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 15:58:33 | ||
图片预览




文档简介
11.2 与三角形有关的角
一、单选题
1.(2022秋·广西桂林·八年级统考期末)如图,,是分别沿着边翻折形成的.若,与交于点,则的度数为( )
A.15° B.20° C.30° D.36°
2.(2022秋·广西钦州·八年级统考期末)如图,把一副三角板叠放在一起.则∠1的大小为( )
A.105° B.115° C.120° D.125°
3.(2022秋·广西河池·八年级统考期末)如图,点是中边上的一点,过作,垂足为.若,则是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
4.(2022秋·广西贵港·八年级统考期末)在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )
A.32° B.36° C.40° D.128°
5.(2022秋·广西梧州·八年级统考期末)三角形的内角和等于( )
A. B. C. D.
6.(2022秋·广西柳州·八年级统考期末)在中,已知,则三角形的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.无法确定
7.(2022秋·广西百色·八年级统考期末)三角形的内角和等于( )
A. B. C. D.
8.(2022秋·广西防城港·八年级统考期末)如图,在△ABC中,已知∠A=80°,∠B=60°,DE∥BC,那么∠CED的大小是( )
A.40° B.60° C.120° D.140°
9.(2022秋·广西防城港·八年级统考期末)如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是( )
A.30° B.40° C.50° D.60°
10.(2022秋·广西河池·八年级统考期末)一副三角板如图叠放在一起,则的度数是( )
A. B. C. D.
11.(2022秋·广西柳州·八年级统考期末)如图,点D是边BC延长线上的一点,,,则( )
A.30° B.35° C.40° D.45°
12.(2022秋·广西贵港·八年级统考期末)在中,,直线,分别与相交于点D,E,若,则∠C的度数是( )
A. B. C. D.
13.(2022秋·广西贺州·八年级统考期末)如图,将一副常规的三角板按如图方式放置,则图中的度数为( )
A. B. C. D.
14.(2022秋·广西百色·八年级统考期末)△ABC中,∠C=50°,∠B=30°,AE平分∠BAC,点F为E上一点,FD⊥DC于点D,则∠EFD=( )
A.5° B.10° C.12° D.20°
二、填空题
15.(2022秋·广西河池·八年级统考期末)已知,如图,在中,,I是,的角平分线的交点,则 °.
16.(2022秋·广西玉林·八年级统考期末)如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2= .
17.(2022秋·广西贺州·八年级统考期末)“三角形三个内角中最多只能有一个直角”,这个命题是 命题(填“真”或“假”).
18.(2022秋·广西桂林·八年级统考期末)若直角三角形的一个锐角为,则另一个锐角的度数是 度.
19.(2022秋·广西崇左·八年级统考期末)如图,,于点,于点,若,则 .
20.(2022秋·广西崇左·八年级统考期末)在直角三角形中,若一个锐角为35°,则另一个锐角为 .
21.(2022秋·广西梧州·八年级统考期末)如图,是的外角,且,,则∠B= 度.
22.(2022秋·广西防城港·八年级统考期末)将一副三角尺按如图方式进行摆放,则∠1的度数为 .
三、解答题
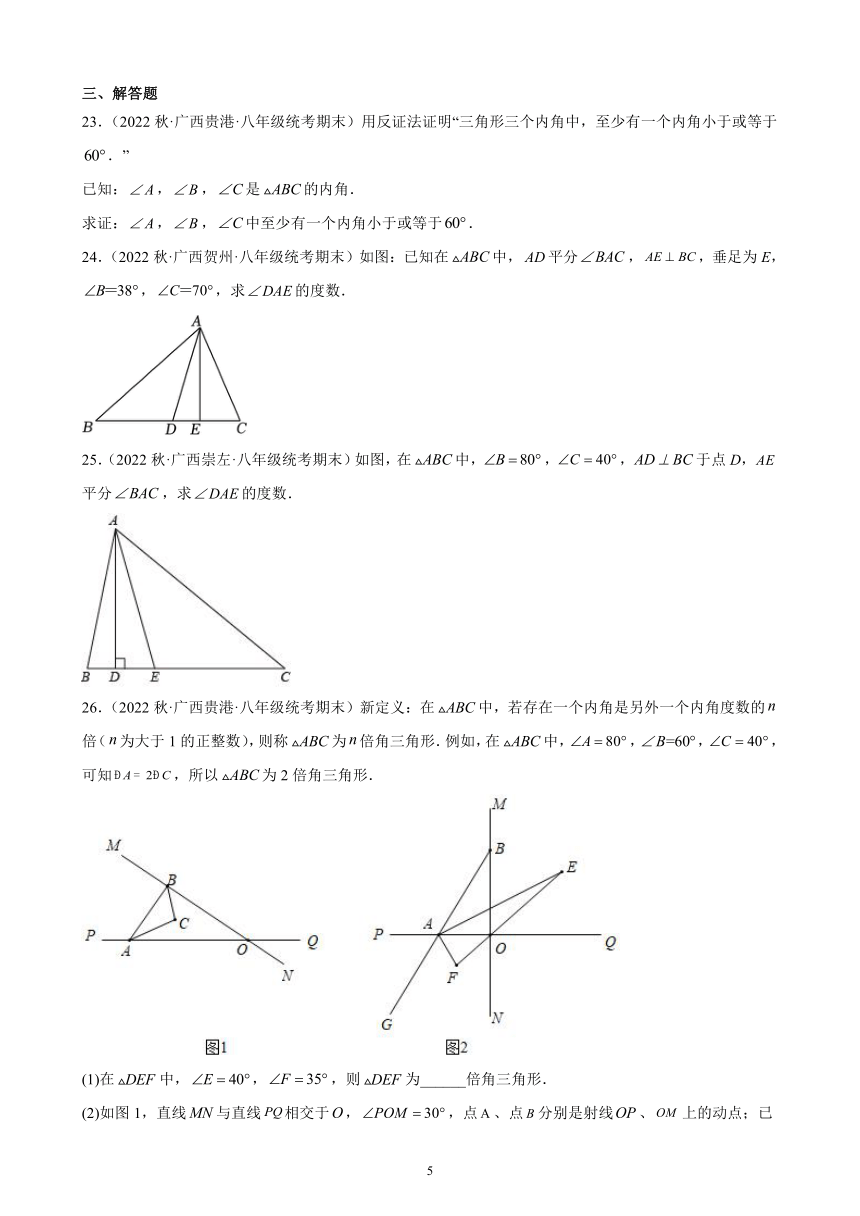
23.(2022秋·广西贵港·八年级统考期末)用反证法证明“三角形三个内角中,至少有一个内角小于或等于.”
已知:,,是的内角.
求证:,,中至少有一个内角小于或等于.
24.(2022秋·广西贺州·八年级统考期末)如图:已知在中,平分,,垂足为E,,,求的度数.
25.(2022秋·广西崇左·八年级统考期末)如图,在中,,,于点D,平分,求的度数.
26.(2022秋·广西贵港·八年级统考期末)新定义:在中,若存在一个内角是另外一个内角度数的倍(为大于1的正整数),则称为倍角三角形.例如,在中,,,,可知,所以为2倍角三角形.
(1)在中,,,则为______倍角三角形.
(2)如图1,直线与直线相交于,,点、点分别是射线、上的动点;已知、的角平分线交于点,在中,如果有一个角是另一个角的2倍,请求出的度数.
(3)如图2,直线直线于点,点、点分别在射线、上,已知、的角平分线分别与的角平分线所在的直线交于点、,若为3倍角三角形,试求的度数.
27.(2022秋·广西梧州·八年级统考期末)如图,在中,,,是的高,是的平分线,求的度数.
28.(2022秋·广西百色·八年级统考期末)已知中,,,点D为BC边上一点,连接AD,作于点E,于点F.
(1)若AD为的角平分线(如图1),图中、有何数量关系?请说明理由.
(2)若AD为的高(如图2),求图中、的度数.
29.(2022秋·广西贺州·八年级统考期末)在△ABC中,已知∠A=105°,∠B-∠C=15°,求∠C的度数.
参考答案:
1.C
【分析】根据∠BCA:∠ABC:∠BAC=28:5:3,三角形的内角和定理分别求得∠BCA,∠ABC,∠BAC的度数,然后根据折叠的性质求出∠D、∠DAE、∠BEA的度数,在△AOD中,根据三角形的内角和定理求出∠AOD的度数,继而可求得∠EOF的度数,最后根据三角形的外角定理求出∠BFC的度数.
【详解】如图所示:
在△ABC中,∵∠BCA:∠ABC:∠BAC=28:5:3,
∴设∠BCA为28x,∠ABC为5x,∠BAC为3x,
则28x+5x+3x=,
解得:x=5,
则∠BCA=140,∠ABC=25,∠BAC=15,
由折叠的性质可得:∠D=25,∠DAE=3∠BAC=45,∠BEA=140,
在△AOD中,∠AOD=180-∠DAE-∠D=110,
∴∠EOF=∠AOD=110,
则∠BFC=∠BEA-∠EOF=140-110=30.
故选:C.
【点睛】考查了图形的折叠变化及三角形的内角和定理.解题关键是要理解折叠前后图形的形状和大小不变,只是位置变化.
2.A
【分析】先根据三角板的性质得出∠A=45°,∠E=30°,再由三角形内角和定理即可得出结论.
【详解】解:如图
∵图中是一副直角三角板,
∴∠A=45°,∠E=30°,
∵
∴
∴
∵
∴.
故选:A.
【点睛】本题考查的是三角形内角和定理、对顶角相等,互余的定义,熟知三角形内角和是180°是解答此题的关键.
3.A
【分析】先求解再证明可得从而可得结论.
【详解】解:
是直角三角形.
故选A
【点睛】本题考查的是垂直的定义,三角形的内角和定理的应用,掌握“三角形的内角和定理”是解本题的关键.
4.A
【分析】直接根据三角形内角和定理求解即可.
【详解】解:∵ ,且∠A=20°,∠B=4∠C,
∴
∴
∴∠C=32°
故选:A.
【点睛】此题主要考查了三角形内角和定理的应用以及解一元一次方程,运用方程思想解答此类试题是常用的思想方法.
5.C
【分析】根据三角形内角和定理即可判断.
【详解】解:∵三角形的内角和等于180°,
故选:C.
【点睛】本题考查了三角形内角和定理,解题关键是熟记三角形内角和定理.
6.B
【分析】设∠A=x,∠B=2x,∠C=3x,根据三角形的内角和等于180°列方程求三个内角的度数,从而确定三角形的形状.
【详解】解:∵
设∠A=x,∠B=2x,∠C=3x.
则x+2x+3x=180°,
解得x=30°,
∴∠A =30°,∠B =60°,∠C =90°,
所以这个三角形是直角三角形.
故选:B.
【点睛】本题主要考查了内角和定理.解答此类题利用三角形内角和定理列方程求解可简化计算.
7.B
【分析】根据三角形的内角和定理进行解答即可.
【详解】因为三角形的内角和等于180度,
故选B.
【点睛】本题主要考查了三角形的内角和定理,熟记“三角形的内角和等于180度“是解题的关键.
8.D
【分析】根据三角形的内角和定理求出∠C,然后根据两直线平行,同旁内角互补即可求出∠CED的大小.
【详解】∵∠A+∠B+∠C=180°(三角形内角和定理),∠A=80°,∠B=60°,
∴∠C=180°-∠A-∠B=180°-80°-60°=40°,
又∵DE∥BC,
∴∠CED+∠C=180°(两直线平行,同旁内角互补).
∴∠CED=180°-40°=140°.
故选D.
【点睛】本题考查三角形的内角和定理和平行线的性质.利用同旁内角互补的性质是解题的关键.
9.B
【详解】解:如图,根据两直线平行,内错角相等,
所以∠3=∠1=50°,
根据对顶角相等和直角三角形两锐角互余得:∠2=90°﹣50°=40°.
故选B.
10.D
【分析】根据三角形的外角定理可得,进而得出,即可得出结论.
【详解】解:如图:
∵,
∴,
∵,
∴,
故选:D.
【点睛】本题主要考查了三角形的外角定理,解题的关键是掌握三角板的内角度数,以及三角形的一个外角等于与它不相邻的两个内角之和.
11.A
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解.
【详解】解:∵,
∴.
故选:A.
【点睛】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.
12.B
【分析】根据三角形的外角性质求得的度数,再根据平行线的性质即可求解.
【详解】解:∵,,
∴,
∵,
∴,
故选:B.
【点睛】本题考查平行线的性质,三角形的外角性质等知识,解题的关键是灵活运用这些知识解决问题.
13.D
【分析】求出的度数,根据三角形的外角性质得到,代入即可.
【详解】解:∵,
∴.
故选:D.
【点睛】本题主要考查对三角形的外角性质的理解和掌握,能熟练地运用三角形的外角性质进行计算是解此题的关键.
14.B
【分析】先求出∠BAE=50°,由外角的性质求出∠FED=80°,然后根据直角三角形两锐角互余即可求出∠EFD的度数.
【详解】∵∠C=50°,∠B=30°,
∴∠BAC=180°﹣∠C﹣∠A=180°﹣50°﹣30°=100°,
∵AE是∠BAC的平分线,
∴∠BAE=50°,
∴∠FED=50°+30°=80°,
又∵DF⊥BC,
∴∠FED+∠EFD=90°,
∴∠EFD=90°﹣80°=10°,
故选:B.
【点睛】本题考查了三角形内角和等于180°,直角三角形中两个锐角互余,三角形外角的性质,角平分线的定义,以及垂直的定义,正确识图是解答本题的关键.
15.130
【分析】由可知,与的平分线交于点,可求的度数,再利用三角形内角和定理求.
【详解】解:(已知),
(三角形内角和定理),
又与的平分线交于点,
,
;
故答案是:130.
【点睛】本题考查了三角形的角平分线、三角形内角和定理.解题时,注意挖掘出隐含在题干中的已知条件:三角形内角和的.
16.
【分析】根据三角形内角和定理,求得,进而根据角平分线的定义求得,进而求得,根据折叠的性质求得,最后根据两个平角减去即可求得.
【详解】∠BA'C=120°,
A'B平分∠ABC,A'C平分∠ACB,
,
,
,
将△ABC纸片沿DE折叠,使点A落在点A'处,
故答案为:
【点睛】考查角平分线的定义以及三角形的内角和定理,三角形的折叠问题,熟练掌握三角形的内角和定理是解题的关键.
17.真
【分析】根据三角形内角和为180°,即可求解.
【详解】解:因为三角形内角和为180°,
所以三角形三个内角中最多只能有一个直角,
所以命题“三角形三个内角中最多只能有一个直角”为真命题.
故答案为:真
【点睛】本题主要考查了判断命题的真假,三角形的内角和定理,熟练掌握三角形内角和为180°是解题的关键.
18.78
【分析】根据直角三角形的两锐角互余计算,得到答案.
【详解】解:∵直角三角形的一个锐角为12°,
∴另一个锐角的度数是:90°-12°=78°,
故答案为:78.
【点睛】本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.
19.
【分析】根据邻补角的概念求出∠EDC,根据直角三角形的性质求出∠C,进而求出∠B,根据直角三角形的性质、平角的概念计算即可.
【详解】解:∵∠ADE=145°,
∴∠EDC=180°﹣145°=35°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠C=90°﹣35°=55°,
∵∠B=∠C,
∴∠B=55°,
∵EF⊥AB,
∴∠EFB=90°,
∴∠BEF=90°﹣55°=35°,
∴∠FED=180°﹣35°﹣90°=55°.
故答案为:55°.
【点睛】本题考查的是直角三角形的性质、垂直的定义,掌握直角三角形的两锐角互余是解题的关键.
20.55°/55度
【分析】直接根据直角三角形的性质即可得出结论.
【详解】∵在直角三角形中,一个锐角为35°
∴另一个锐角=90° 35°=55°
故答案为55°.
【点睛】本题考查直角三角形的性质,解题的关键是熟悉直角三角形的性质.
21.30
【分析】根据三角形的内角与外角之间的关系解答即可.
【详解】解:∵,,
∴.
故答案为:30.
【点睛】本题主要考查了三角形的内角和外角之间的关系,掌握三角形的外角等于与它不相邻的两个内角和是解题关键.
22.120°/120度
【分析】由题意得∠ACB=∠QFP=90°,∠A=60°,根据三角形外角性质求出∠ACF的度数,再求出∠FCB的度数,即可求出∠1.
【详解】解:如图,
由题意得∠ACB=∠QFP=90°,∠A=60°,
∴∠ACF=∠QFP-∠A=30°,
∴∠FCB=∠ACB-∠ACF=60°,
∴∠1=180°-∠FCB=120°,
故答案为:120°.
【点睛】此题考查了利用三角板求角度,三角形外角的性质,利用邻补角求角的度数,正确掌握三角板中各角度是解题的关键.
23.见解析
【分析】根据反证法证明方法,先假设结论不成立,然后得到与定理矛盾,从而证得原结论成立.
【详解】证明:假设求证的结论不成立,那么三角形中所有角都大于,
,
这与三角形的三内角和为相矛盾.
假设不成立,
三角形三内角中至少有一个内角小于或等于度.
【点睛】本题考查了三角形内角和定理考查反证法,解题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时,要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
24.
【分析】由,,得,由平分,求出,再求出,进而求出.
【详解】∵,,
∴
∵平分,
∴
∵,
∴.
∵,
∴
∴.
【点睛】本题考查三角形内角和定理,解题的关键是根据已知角的度数,求出相应角的度数.
25.
【分析】利用三角形内角和定理求出,再利用AE平分求出,进一步求出,利用,即可求出.
【详解】解:∵在中,,,
∴ ,
∵ AE平分,
∴,
∴,
∵,
∴,
∴
【点睛】本题考查三角形内角和定理,角平分线的性质,垂直.解题的关键是熟练掌握三角形内角和定理,找出角度之间的关系进行计算.
26.(1)3
(2)50°、52.5°、25°或22.5°
(3)45°或60°
【分析】(1)由∠E=40°,∠F=35°可知∠D=105°,再根据n倍角三角形的定义可得结论.
(2)根据三角形内角和定理及一个外角等于与它不相邻的两个内角和,利用角的和差计算即可求得结果.
(3)首先证明∠EAF=90°,分四种情形分别求出即可.
【详解】(1)∵∠E=40°,∠F=35°,
∴∠D=180°-40°-35°=105°,
∴∠D=3∠F,
∴△ABC为3倍角三角形,
故答案为:3;
(2)∵∠POM=30°,
∴∠OAB+∠OBA=150°.
又∵BC平分∠OBA,AC平分∠OAB,
∴∠CBA+∠CAB=∠OAB+∠OBA=75°,
∴∠C=105°.
①当∠CBA=2∠CAB时,∵∠CBA+∠CAB=75°,
∴∠BAC=25°;
②当∠CAB=2∠CBA时,∵∠CBA+∠CAB=75°,
∴∠BAC=50°;
③当∠C=2∠CAB时,∵∠C=105°,
∴∠BAC=∠C=52.5°;
④当∠C=2∠CBA时,∵∠C=105°,
∴∠CBA=∠C=52.5°,
∴∠BAC=22.5°.
综上,在△ABC中当一个角是另一个角的2倍时,∠BAC等于50°、52.5°、25°或22.5°;
(3)∵AE平分∠BAO,AF平分∠OAG,
∴∠BAE=∠EAO,∠OAF=∠GAF,
∴∠EAF=∠EAO+∠OAF=90°,
∴∠E+∠F=90°;
又∵EF平分∠BOQ,
∴∠EOQ=∠E+∠EAO=45°①,
∠BOQ=∠ABO+∠BAO=90° ②;
①×2-②得:∠ABO=2∠E.
若△AEF为3倍角三角形:
i)若∠F=3∠E,∵∠E+∠F=90°,
∴∠E=22.5°,
∴∠ABO=45°;
ii)若∠E=3∠F,
∴∠E=67.5°,
∴∠ABO=135°(不符合题意,舍去);
iii)若∠EAF=3∠E,∴∠E=30°,
∴∠ABO=60°;
iv)若∠EAF=3∠F,∴∠F=30°,∠E=60°,
∴∠ABO=120°(不符合题意,舍去);
综上所述,∠ABO等于45°或60°时,△AEF为3倍角三角形.
【点睛】本题主要考查了三角形的内角和定理,余角的意义,不等式组的解法和应用等知识,读懂新定义n倍角三角形的意义和分类讨论是解决问题的基础和关键.
27.
【分析】由是的高,得到,由三角形内角和定理得到,,由是的平分线,得到,即可得到答案.
【详解】解:∵是的高,
∴,
∵,,,
∴,,
∵是的平分线,
∴,
∴.
【点睛】本题主要考查了三角形的内角和定理、角平分线的定义、高的定义,解答此题的关键是要明确三角形的内角和是.
28.(1),理由见解析;(2),
【详解】解:(1)∵AD为的角平分线
∴
又∵,
∴
∴
即
(2)∵AD为的高
∴
又∵
∴
又∵
∴
又∵,
∴,
∴
【点睛】本题主要考查了三角形内角和定理及直角三角形中两锐角的性质,熟练掌握三角形内角和定理及直角三角形中两锐角互余的性质是解题的关键
29.30°
【分析】由∠B-∠C=15°,可得∠B=∠C+15°,然后根据三角形内角和等于180°求解即可.
【详解】∵∠B-∠C=15°,
∴∠B=∠C+15°,
∵∠A+∠B+∠C=180°,
∴105°+∠C+15°+∠C=180°,
∴∠C=30°.
【点睛】本题考查了三角形的内角和定理,熟练掌握三角形三个内角的和等于180°是解答本题的关键.
一、单选题
1.(2022秋·广西桂林·八年级统考期末)如图,,是分别沿着边翻折形成的.若,与交于点,则的度数为( )
A.15° B.20° C.30° D.36°
2.(2022秋·广西钦州·八年级统考期末)如图,把一副三角板叠放在一起.则∠1的大小为( )
A.105° B.115° C.120° D.125°
3.(2022秋·广西河池·八年级统考期末)如图,点是中边上的一点,过作,垂足为.若,则是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
4.(2022秋·广西贵港·八年级统考期末)在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )
A.32° B.36° C.40° D.128°
5.(2022秋·广西梧州·八年级统考期末)三角形的内角和等于( )
A. B. C. D.
6.(2022秋·广西柳州·八年级统考期末)在中,已知,则三角形的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.无法确定
7.(2022秋·广西百色·八年级统考期末)三角形的内角和等于( )
A. B. C. D.
8.(2022秋·广西防城港·八年级统考期末)如图,在△ABC中,已知∠A=80°,∠B=60°,DE∥BC,那么∠CED的大小是( )
A.40° B.60° C.120° D.140°
9.(2022秋·广西防城港·八年级统考期末)如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是( )
A.30° B.40° C.50° D.60°
10.(2022秋·广西河池·八年级统考期末)一副三角板如图叠放在一起,则的度数是( )
A. B. C. D.
11.(2022秋·广西柳州·八年级统考期末)如图,点D是边BC延长线上的一点,,,则( )
A.30° B.35° C.40° D.45°
12.(2022秋·广西贵港·八年级统考期末)在中,,直线,分别与相交于点D,E,若,则∠C的度数是( )
A. B. C. D.
13.(2022秋·广西贺州·八年级统考期末)如图,将一副常规的三角板按如图方式放置,则图中的度数为( )
A. B. C. D.
14.(2022秋·广西百色·八年级统考期末)△ABC中,∠C=50°,∠B=30°,AE平分∠BAC,点F为E上一点,FD⊥DC于点D,则∠EFD=( )
A.5° B.10° C.12° D.20°
二、填空题
15.(2022秋·广西河池·八年级统考期末)已知,如图,在中,,I是,的角平分线的交点,则 °.
16.(2022秋·广西玉林·八年级统考期末)如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2= .
17.(2022秋·广西贺州·八年级统考期末)“三角形三个内角中最多只能有一个直角”,这个命题是 命题(填“真”或“假”).
18.(2022秋·广西桂林·八年级统考期末)若直角三角形的一个锐角为,则另一个锐角的度数是 度.
19.(2022秋·广西崇左·八年级统考期末)如图,,于点,于点,若,则 .
20.(2022秋·广西崇左·八年级统考期末)在直角三角形中,若一个锐角为35°,则另一个锐角为 .
21.(2022秋·广西梧州·八年级统考期末)如图,是的外角,且,,则∠B= 度.
22.(2022秋·广西防城港·八年级统考期末)将一副三角尺按如图方式进行摆放,则∠1的度数为 .
三、解答题
23.(2022秋·广西贵港·八年级统考期末)用反证法证明“三角形三个内角中,至少有一个内角小于或等于.”
已知:,,是的内角.
求证:,,中至少有一个内角小于或等于.
24.(2022秋·广西贺州·八年级统考期末)如图:已知在中,平分,,垂足为E,,,求的度数.
25.(2022秋·广西崇左·八年级统考期末)如图,在中,,,于点D,平分,求的度数.
26.(2022秋·广西贵港·八年级统考期末)新定义:在中,若存在一个内角是另外一个内角度数的倍(为大于1的正整数),则称为倍角三角形.例如,在中,,,,可知,所以为2倍角三角形.
(1)在中,,,则为______倍角三角形.
(2)如图1,直线与直线相交于,,点、点分别是射线、上的动点;已知、的角平分线交于点,在中,如果有一个角是另一个角的2倍,请求出的度数.
(3)如图2,直线直线于点,点、点分别在射线、上,已知、的角平分线分别与的角平分线所在的直线交于点、,若为3倍角三角形,试求的度数.
27.(2022秋·广西梧州·八年级统考期末)如图,在中,,,是的高,是的平分线,求的度数.
28.(2022秋·广西百色·八年级统考期末)已知中,,,点D为BC边上一点,连接AD,作于点E,于点F.
(1)若AD为的角平分线(如图1),图中、有何数量关系?请说明理由.
(2)若AD为的高(如图2),求图中、的度数.
29.(2022秋·广西贺州·八年级统考期末)在△ABC中,已知∠A=105°,∠B-∠C=15°,求∠C的度数.
参考答案:
1.C
【分析】根据∠BCA:∠ABC:∠BAC=28:5:3,三角形的内角和定理分别求得∠BCA,∠ABC,∠BAC的度数,然后根据折叠的性质求出∠D、∠DAE、∠BEA的度数,在△AOD中,根据三角形的内角和定理求出∠AOD的度数,继而可求得∠EOF的度数,最后根据三角形的外角定理求出∠BFC的度数.
【详解】如图所示:
在△ABC中,∵∠BCA:∠ABC:∠BAC=28:5:3,
∴设∠BCA为28x,∠ABC为5x,∠BAC为3x,
则28x+5x+3x=,
解得:x=5,
则∠BCA=140,∠ABC=25,∠BAC=15,
由折叠的性质可得:∠D=25,∠DAE=3∠BAC=45,∠BEA=140,
在△AOD中,∠AOD=180-∠DAE-∠D=110,
∴∠EOF=∠AOD=110,
则∠BFC=∠BEA-∠EOF=140-110=30.
故选:C.
【点睛】考查了图形的折叠变化及三角形的内角和定理.解题关键是要理解折叠前后图形的形状和大小不变,只是位置变化.
2.A
【分析】先根据三角板的性质得出∠A=45°,∠E=30°,再由三角形内角和定理即可得出结论.
【详解】解:如图
∵图中是一副直角三角板,
∴∠A=45°,∠E=30°,
∵
∴
∴
∵
∴.
故选:A.
【点睛】本题考查的是三角形内角和定理、对顶角相等,互余的定义,熟知三角形内角和是180°是解答此题的关键.
3.A
【分析】先求解再证明可得从而可得结论.
【详解】解:
是直角三角形.
故选A
【点睛】本题考查的是垂直的定义,三角形的内角和定理的应用,掌握“三角形的内角和定理”是解本题的关键.
4.A
【分析】直接根据三角形内角和定理求解即可.
【详解】解:∵ ,且∠A=20°,∠B=4∠C,
∴
∴
∴∠C=32°
故选:A.
【点睛】此题主要考查了三角形内角和定理的应用以及解一元一次方程,运用方程思想解答此类试题是常用的思想方法.
5.C
【分析】根据三角形内角和定理即可判断.
【详解】解:∵三角形的内角和等于180°,
故选:C.
【点睛】本题考查了三角形内角和定理,解题关键是熟记三角形内角和定理.
6.B
【分析】设∠A=x,∠B=2x,∠C=3x,根据三角形的内角和等于180°列方程求三个内角的度数,从而确定三角形的形状.
【详解】解:∵
设∠A=x,∠B=2x,∠C=3x.
则x+2x+3x=180°,
解得x=30°,
∴∠A =30°,∠B =60°,∠C =90°,
所以这个三角形是直角三角形.
故选:B.
【点睛】本题主要考查了内角和定理.解答此类题利用三角形内角和定理列方程求解可简化计算.
7.B
【分析】根据三角形的内角和定理进行解答即可.
【详解】因为三角形的内角和等于180度,
故选B.
【点睛】本题主要考查了三角形的内角和定理,熟记“三角形的内角和等于180度“是解题的关键.
8.D
【分析】根据三角形的内角和定理求出∠C,然后根据两直线平行,同旁内角互补即可求出∠CED的大小.
【详解】∵∠A+∠B+∠C=180°(三角形内角和定理),∠A=80°,∠B=60°,
∴∠C=180°-∠A-∠B=180°-80°-60°=40°,
又∵DE∥BC,
∴∠CED+∠C=180°(两直线平行,同旁内角互补).
∴∠CED=180°-40°=140°.
故选D.
【点睛】本题考查三角形的内角和定理和平行线的性质.利用同旁内角互补的性质是解题的关键.
9.B
【详解】解:如图,根据两直线平行,内错角相等,
所以∠3=∠1=50°,
根据对顶角相等和直角三角形两锐角互余得:∠2=90°﹣50°=40°.
故选B.
10.D
【分析】根据三角形的外角定理可得,进而得出,即可得出结论.
【详解】解:如图:
∵,
∴,
∵,
∴,
故选:D.
【点睛】本题主要考查了三角形的外角定理,解题的关键是掌握三角板的内角度数,以及三角形的一个外角等于与它不相邻的两个内角之和.
11.A
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解.
【详解】解:∵,
∴.
故选:A.
【点睛】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.
12.B
【分析】根据三角形的外角性质求得的度数,再根据平行线的性质即可求解.
【详解】解:∵,,
∴,
∵,
∴,
故选:B.
【点睛】本题考查平行线的性质,三角形的外角性质等知识,解题的关键是灵活运用这些知识解决问题.
13.D
【分析】求出的度数,根据三角形的外角性质得到,代入即可.
【详解】解:∵,
∴.
故选:D.
【点睛】本题主要考查对三角形的外角性质的理解和掌握,能熟练地运用三角形的外角性质进行计算是解此题的关键.
14.B
【分析】先求出∠BAE=50°,由外角的性质求出∠FED=80°,然后根据直角三角形两锐角互余即可求出∠EFD的度数.
【详解】∵∠C=50°,∠B=30°,
∴∠BAC=180°﹣∠C﹣∠A=180°﹣50°﹣30°=100°,
∵AE是∠BAC的平分线,
∴∠BAE=50°,
∴∠FED=50°+30°=80°,
又∵DF⊥BC,
∴∠FED+∠EFD=90°,
∴∠EFD=90°﹣80°=10°,
故选:B.
【点睛】本题考查了三角形内角和等于180°,直角三角形中两个锐角互余,三角形外角的性质,角平分线的定义,以及垂直的定义,正确识图是解答本题的关键.
15.130
【分析】由可知,与的平分线交于点,可求的度数,再利用三角形内角和定理求.
【详解】解:(已知),
(三角形内角和定理),
又与的平分线交于点,
,
;
故答案是:130.
【点睛】本题考查了三角形的角平分线、三角形内角和定理.解题时,注意挖掘出隐含在题干中的已知条件:三角形内角和的.
16.
【分析】根据三角形内角和定理,求得,进而根据角平分线的定义求得,进而求得,根据折叠的性质求得,最后根据两个平角减去即可求得.
【详解】∠BA'C=120°,
A'B平分∠ABC,A'C平分∠ACB,
,
,
,
将△ABC纸片沿DE折叠,使点A落在点A'处,
故答案为:
【点睛】考查角平分线的定义以及三角形的内角和定理,三角形的折叠问题,熟练掌握三角形的内角和定理是解题的关键.
17.真
【分析】根据三角形内角和为180°,即可求解.
【详解】解:因为三角形内角和为180°,
所以三角形三个内角中最多只能有一个直角,
所以命题“三角形三个内角中最多只能有一个直角”为真命题.
故答案为:真
【点睛】本题主要考查了判断命题的真假,三角形的内角和定理,熟练掌握三角形内角和为180°是解题的关键.
18.78
【分析】根据直角三角形的两锐角互余计算,得到答案.
【详解】解:∵直角三角形的一个锐角为12°,
∴另一个锐角的度数是:90°-12°=78°,
故答案为:78.
【点睛】本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.
19.
【分析】根据邻补角的概念求出∠EDC,根据直角三角形的性质求出∠C,进而求出∠B,根据直角三角形的性质、平角的概念计算即可.
【详解】解:∵∠ADE=145°,
∴∠EDC=180°﹣145°=35°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠C=90°﹣35°=55°,
∵∠B=∠C,
∴∠B=55°,
∵EF⊥AB,
∴∠EFB=90°,
∴∠BEF=90°﹣55°=35°,
∴∠FED=180°﹣35°﹣90°=55°.
故答案为:55°.
【点睛】本题考查的是直角三角形的性质、垂直的定义,掌握直角三角形的两锐角互余是解题的关键.
20.55°/55度
【分析】直接根据直角三角形的性质即可得出结论.
【详解】∵在直角三角形中,一个锐角为35°
∴另一个锐角=90° 35°=55°
故答案为55°.
【点睛】本题考查直角三角形的性质,解题的关键是熟悉直角三角形的性质.
21.30
【分析】根据三角形的内角与外角之间的关系解答即可.
【详解】解:∵,,
∴.
故答案为:30.
【点睛】本题主要考查了三角形的内角和外角之间的关系,掌握三角形的外角等于与它不相邻的两个内角和是解题关键.
22.120°/120度
【分析】由题意得∠ACB=∠QFP=90°,∠A=60°,根据三角形外角性质求出∠ACF的度数,再求出∠FCB的度数,即可求出∠1.
【详解】解:如图,
由题意得∠ACB=∠QFP=90°,∠A=60°,
∴∠ACF=∠QFP-∠A=30°,
∴∠FCB=∠ACB-∠ACF=60°,
∴∠1=180°-∠FCB=120°,
故答案为:120°.
【点睛】此题考查了利用三角板求角度,三角形外角的性质,利用邻补角求角的度数,正确掌握三角板中各角度是解题的关键.
23.见解析
【分析】根据反证法证明方法,先假设结论不成立,然后得到与定理矛盾,从而证得原结论成立.
【详解】证明:假设求证的结论不成立,那么三角形中所有角都大于,
,
这与三角形的三内角和为相矛盾.
假设不成立,
三角形三内角中至少有一个内角小于或等于度.
【点睛】本题考查了三角形内角和定理考查反证法,解题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时,要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
24.
【分析】由,,得,由平分,求出,再求出,进而求出.
【详解】∵,,
∴
∵平分,
∴
∵,
∴.
∵,
∴
∴.
【点睛】本题考查三角形内角和定理,解题的关键是根据已知角的度数,求出相应角的度数.
25.
【分析】利用三角形内角和定理求出,再利用AE平分求出,进一步求出,利用,即可求出.
【详解】解:∵在中,,,
∴ ,
∵ AE平分,
∴,
∴,
∵,
∴,
∴
【点睛】本题考查三角形内角和定理,角平分线的性质,垂直.解题的关键是熟练掌握三角形内角和定理,找出角度之间的关系进行计算.
26.(1)3
(2)50°、52.5°、25°或22.5°
(3)45°或60°
【分析】(1)由∠E=40°,∠F=35°可知∠D=105°,再根据n倍角三角形的定义可得结论.
(2)根据三角形内角和定理及一个外角等于与它不相邻的两个内角和,利用角的和差计算即可求得结果.
(3)首先证明∠EAF=90°,分四种情形分别求出即可.
【详解】(1)∵∠E=40°,∠F=35°,
∴∠D=180°-40°-35°=105°,
∴∠D=3∠F,
∴△ABC为3倍角三角形,
故答案为:3;
(2)∵∠POM=30°,
∴∠OAB+∠OBA=150°.
又∵BC平分∠OBA,AC平分∠OAB,
∴∠CBA+∠CAB=∠OAB+∠OBA=75°,
∴∠C=105°.
①当∠CBA=2∠CAB时,∵∠CBA+∠CAB=75°,
∴∠BAC=25°;
②当∠CAB=2∠CBA时,∵∠CBA+∠CAB=75°,
∴∠BAC=50°;
③当∠C=2∠CAB时,∵∠C=105°,
∴∠BAC=∠C=52.5°;
④当∠C=2∠CBA时,∵∠C=105°,
∴∠CBA=∠C=52.5°,
∴∠BAC=22.5°.
综上,在△ABC中当一个角是另一个角的2倍时,∠BAC等于50°、52.5°、25°或22.5°;
(3)∵AE平分∠BAO,AF平分∠OAG,
∴∠BAE=∠EAO,∠OAF=∠GAF,
∴∠EAF=∠EAO+∠OAF=90°,
∴∠E+∠F=90°;
又∵EF平分∠BOQ,
∴∠EOQ=∠E+∠EAO=45°①,
∠BOQ=∠ABO+∠BAO=90° ②;
①×2-②得:∠ABO=2∠E.
若△AEF为3倍角三角形:
i)若∠F=3∠E,∵∠E+∠F=90°,
∴∠E=22.5°,
∴∠ABO=45°;
ii)若∠E=3∠F,
∴∠E=67.5°,
∴∠ABO=135°(不符合题意,舍去);
iii)若∠EAF=3∠E,∴∠E=30°,
∴∠ABO=60°;
iv)若∠EAF=3∠F,∴∠F=30°,∠E=60°,
∴∠ABO=120°(不符合题意,舍去);
综上所述,∠ABO等于45°或60°时,△AEF为3倍角三角形.
【点睛】本题主要考查了三角形的内角和定理,余角的意义,不等式组的解法和应用等知识,读懂新定义n倍角三角形的意义和分类讨论是解决问题的基础和关键.
27.
【分析】由是的高,得到,由三角形内角和定理得到,,由是的平分线,得到,即可得到答案.
【详解】解:∵是的高,
∴,
∵,,,
∴,,
∵是的平分线,
∴,
∴.
【点睛】本题主要考查了三角形的内角和定理、角平分线的定义、高的定义,解答此题的关键是要明确三角形的内角和是.
28.(1),理由见解析;(2),
【详解】解:(1)∵AD为的角平分线
∴
又∵,
∴
∴
即
(2)∵AD为的高
∴
又∵
∴
又∵
∴
又∵,
∴,
∴
【点睛】本题主要考查了三角形内角和定理及直角三角形中两锐角的性质,熟练掌握三角形内角和定理及直角三角形中两锐角互余的性质是解题的关键
29.30°
【分析】由∠B-∠C=15°,可得∠B=∠C+15°,然后根据三角形内角和等于180°求解即可.
【详解】∵∠B-∠C=15°,
∴∠B=∠C+15°,
∵∠A+∠B+∠C=180°,
∴105°+∠C+15°+∠C=180°,
∴∠C=30°.
【点睛】本题考查了三角形的内角和定理,熟练掌握三角形三个内角的和等于180°是解答本题的关键.
