12.2 三角形全等的判定 同步练习 (含解析)2022-2023学年上学期广西各地八年级数学期末试题选编
文档属性
| 名称 | 12.2 三角形全等的判定 同步练习 (含解析)2022-2023学年上学期广西各地八年级数学期末试题选编 |  | |
| 格式 | docx | ||
| 文件大小 | 954.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 16:19:34 | ||
图片预览

文档简介
12.2 三角形全等的判定
一、单选题
1.(2022秋·广西贺州·八年级统考期末)如图,通过尺规作图得到的依据是( )
A.SSS B.SAS C.ASA D.AAS
2.(2022秋·广西崇左·八年级统考期末)如图,AC与BD相交于点O,∠1=∠2,若用“SAS”说明△ABC≌△BAD,则还需添加的一个条件是( )
A.AD=BC B.∠C=∠D C.AO=BO D.AC=BD
3.(2022秋·广西南宁·八年级统考期末)如图,在中,,是高,能直接判断的依据是( )
A. B. C. D.
4.(2022秋·广西崇左·八年级统考期末)如图,已知,要使,只需增加的一个条件( )
A. B.
C. D.
5.(2022秋·广西梧州·八年级统考期末)在三角形全等判定定理中,下列哪一个不属于三角形全等判定定理简记( )
A. B. C. D.
6.(2022秋·广西河池·八年级统考期末)如图,为测量桃李湖两端AB的距离,南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C,测得∠ACB的度数,在AC的另一侧测得∠ACD=∠ACB,CD=CB,再测得AD的长,就是AB的长.那么判定△ABC≌△ADC的理由是( )
A.SAS B.SSS C.ASA D.AAS
7.(2022秋·广西百色·八年级统考期末)如图为6个边长相等的正方形组成的图形,则∠1+∠2+∠3的大小是( )
A.90° B.120° C.135° D.150°
8.(2022秋·广西梧州·八年级统考期末)如图,在等腰直角三角形中,,点B在直线l上,过A作于D,过C作于E.下列给出四个结论:①;②与互余;③.其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
9.(2022秋·广西贵港·八年级统考期末)如图,在中,点在边上,是边的中点,//,与的延长线交于点,若,,则的长为 .
10.(2022秋·广西桂林·八年级统考期末)如图是由九个边长为1的小正方形拼成的大正方形,图中∠1+∠2+∠3+∠4+∠5的度数为 .
11.(2022秋·广西北海·八年级统考期末)如图,已知,,,则 .
12.(2022秋·广西贺州·八年级统考期末)如图,点B、E、C、F在同一直线上,AB=DE,BE=CF,要使△ABC≌△DEF,需添加的条件是 (添加一个即可).
13.(2022秋·广西河池·八年级统考期末)如图所示,AD是△ABC中BC边上的中线,若AB=2,AC=6,则AD的取值范围是
三、解答题
14.(2022秋·广西河池·八年级统考期末)如图,,.求证:.
15.(2022秋·广西崇左·八年级统考期末)如图,BD=AC,OB=OA,求证:△AOD≌△BOC.
16.(2022秋·广西柳州·八年级统考期末)如图,点B,F,C,E在同一条直线上,,,.求证:.
17.(2022秋·广西贺州·八年级统考期末)如图,点B、F、C、E在同一条直线上,,,求证:.
18.(2022秋·广西贵港·八年级统考期末)尺规作图(只保留作图痕迹,不要求写出作法):
如图,已知线段和,求作,使,,.
19.(2022秋·广西河池·八年级统考期末)如图,已知点B、E、C、F在同一直线上,,,.求证:
(1);
(2).
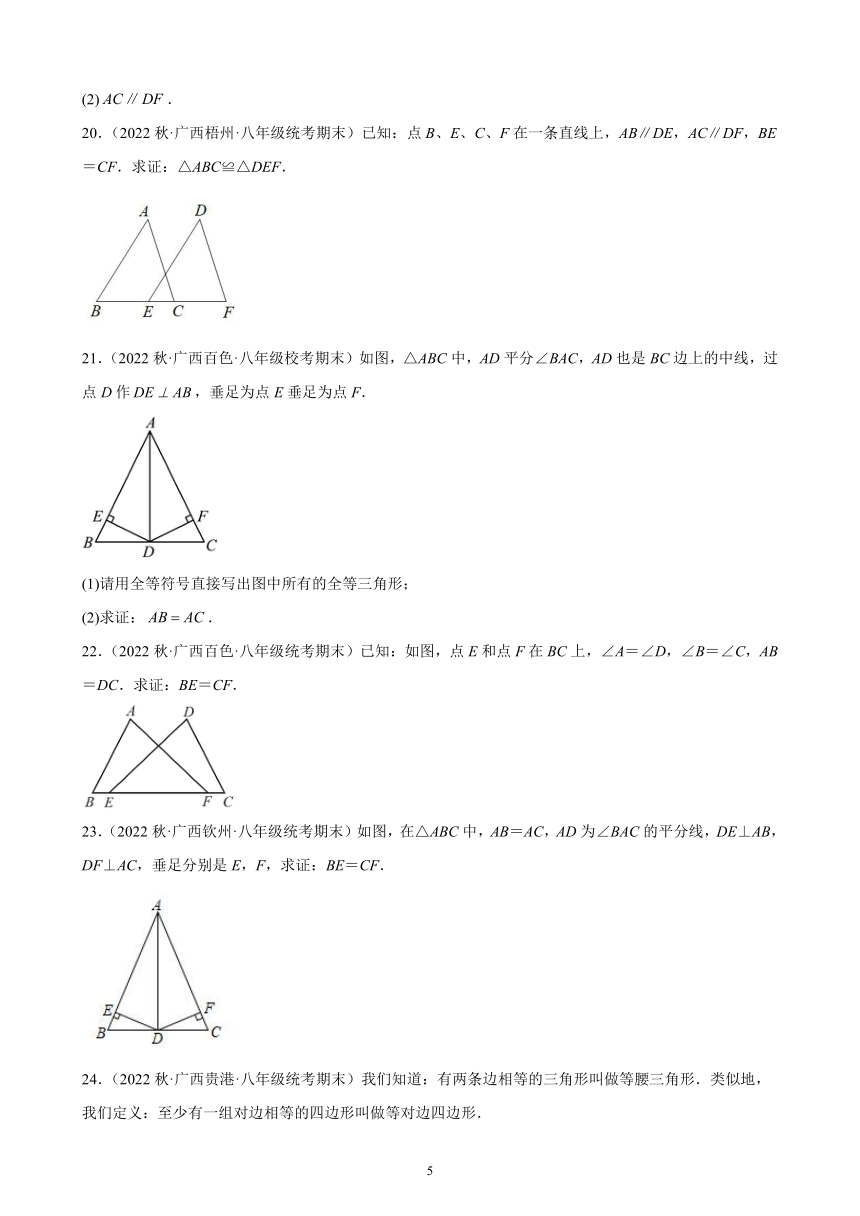
20.(2022秋·广西梧州·八年级统考期末)已知:点B、E、C、F在一条直线上,AB∥DE,AC∥DF,BE=CF.求证:△ABC≌△DEF.
21.(2022秋·广西百色·八年级校考期末)如图,△ABC中,AD平分∠BAC,AD也是BC边上的中线,过点D作,垂足为点E垂足为点F.
(1)请用全等符号直接写出图中所有的全等三角形;
(2)求证:.
22.(2022秋·广西百色·八年级统考期末)已知:如图,点E和点F在BC上,∠A=∠D,∠B=∠C,AB=DC.求证:BE=CF.
23.(2022秋·广西钦州·八年级统考期末)如图,在△ABC中,AB=AC,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,求证:BE=CF.
24.(2022秋·广西贵港·八年级统考期末)我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
(2)如图,在中,点、分别在、上,与相交于点,若.
①请你写出图中一个与相等的角;
②证明四边形是等对边四边形.
25.(2022秋·广西崇左·八年级统考期末)如图,在和中,点在边上,,,,与交于点.
(1)求证:;
(2)若,,求的度数.
26.(2022秋·广西河池·八年级统考期末)在中,,直线经过点,于,于.
(1)当直线绕点旋转到图(1)的位置时,求证:;
(2)当直线绕点旋转到图(2)的位置时,此时,,求的长度.
27.(2022秋·广西桂林·八年级统考期末)如图,在五边形中,,.
(1)请你添加一个与角有关的条件,使得,并说明理由;
(2)在(1)的条件下,若,,求的度数.
28.(2022秋·广西百色·八年级统考期末)如图,在△ABC中,AB=AC,点,在边上,.求证:.
参考答案:
1.A
【分析】根据作图过程利用可以证明,进而可得结论.
【详解】解:根据作图过程可知,
在和中,
,
∴,
∴(全等三角形的对应角相等).
故选:A.
【点睛】本题考查了全等三角形的判定与性质,解决本题的关键是掌握基本作图方法.
2.D
【分析】根据全等三角形的判定,已知∠1=∠2,AB为公共边,所以可添加AC=BD,根据SAS可证△ABC≌△BAD.
【详解】解:添加AC=BD,理由如下:
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS),
故选:D.
【点睛】此题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
3.C
【分析】根据直角三角形的全等证明即可判断.
【详解】证明:∵AD⊥BC
∴和是直角三角形,
∵,AD=AD(公共边),
所以≌(HL)
故选C
【点睛】本题主要考查直角三角形的全等证明,掌握直角三角形的全等证明方法是解题的关键.
4.C
【分析】结合图形,发现BC=CB是公共边,选择SAS判断即可.
【详解】∵AC=DB,BC=CB,
∴选择SAS判断,
故选C.
【点睛】本题考查了三角形全等的判定定理,熟练掌握定理并结合已知选择适当原理是解题的关键.
5.B
【分析】根据全等三角形的判定定理分析判断即可.
【详解】解:全等三角形的判定定理分别为:
(1)判定定理1:-三条边分别对应相等的两个三角形全等.
(2)判定定理2:-两边及其夹角分别对应相等的两个三角形全等.故C不符合题意;
(3)判定定理3:-两角及其夹边分别对应相等的两个三角形全等;
(4)判定定理4:-两角及其中一个角的对边对应相等的两个三角形全等.故A不符合题意;
(5)判定定理5:-斜边与直角边对应相等的两个直角三角形全等.故D不符合题意.
全等三角形的判定定理不存在.故B符合题意.
故选:B.
【点睛】本题考查了全等三角形的判定,熟记全等三角形的判定方法是解题的关键.注意:、不能判定两个三角形全等.
6.A
【分析】已知条件是∠ACD=∠ACB,CD=CB,AC=AC,据此作出选择.
【详解】解:在△ADC与△ABC中,
.
∴△ADC≌△ABC(SAS).
故选:A.
【点睛】此题考查了全等三角形的应用,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS,做题时注意选择.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
7.C
【分析】标注字母,利用“边角边”判断出和全等,根据全等三角形对应角相等可得(或观察图形得到,然后求出,再判断出,然后计算即可得解.
【详解】解:如图,在和中,
,
,
(或观察图形得到,
,
,
又,
.
故选:C.
【点睛】本题考查了全等图形,网格结构,解题的关键是准确识图判断出全等的三角形.
8.D
【分析】证△ADB≌△BEC即可.
【详解】证明:∵, ,
∴∠ADB=∠BEC=90°,
∴∠BAD+∠ABD=90°,∠BCE+∠CBE=90°,
∵,
∴∠ABD+∠CBE=90°,
∴∠BAD=∠CBE,
∴∠BCE+∠BAD=90°,故②正确;
∵∠BAD=∠CBE,∠ADB=∠BEC=90°,
∴△ADB≌△BEC,
∴,AD=BE,故①正确;
DE=DB+BE=CE+AD,故③正确;
故选:D.
【点睛】本题考查了全等三角形的判定与性质,解题关键是找到并证明全等三角形.
9.1
【分析】由平行线及中点的性质得出, ,,利用全等三角形的判定和性质及线段间的数量关系即可得出结果.
【详解】解:∵,
∴, ,
∵E是AC边的中点,
∴,
在与中,
,
∴,
∴,
∴,
故答案为:1.
【点睛】题目主要考查全等三角形的判定和性质,平行线的性质等,理解题意,熟练掌握运用各个知识点是解题关键.
10.225°
【分析】首先判定△ABC≌△AEF,△ABD≌△AEH,可得∠5=∠BCA,∠4=∠BDA,然后可得∠1+∠5=∠1+∠BCA=90°,∠2+∠4=∠2+∠BDA=90°,即可求得∠1+∠2+∠3+∠4+∠5的值.
【详解】解:如图所示:
在△ABC和△AEF中,
∴△ABC≌△AEF(SAS),
∴∠5=∠BCA,
∴∠1+∠5=∠1+∠BCA=90°,
在Rt△ABD和Rt△AEH中,
∴Rt△ABD≌Rt△AEH(HL),
∴∠4=∠BDA,
∴∠2+∠4=∠2+∠BDA=90°,
∵∠3=45°,
∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°.
故答案为:225°.
【点睛】此题主要考查了全等三角形的判定和性质,关键是掌握全等三角形的性质:全等三角形对应角相等即可求解.
11.50°
【分析】根据题意证明Rt△ABC≌Rt△ADC,得到∠DAC=∠BAC=40°,根据直角三角形两锐角互余计算即可.
【详解】解:在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠DAC=∠BAC=40°,
∴∠DCA=90°-40°=50°,
故答案为:50°.
【点睛】本题考查的是全等三角形的判定和性质,掌握直角三角形全等的判定定理是解题的关键.
12.∠B=∠DEF或AC=DF
【分析】根据题意,可知两个三角形的两条边相等,只需再加上夹角或者另一条边相等即可证明两个三角形全等.
【详解】,
,即,
又∵,
可添加,利用SAS来证明三角形全等,
也可添加,利用SSS来证明三角形全等,
故答案为: 或.
【点睛】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法,即SSS、SAS、ASA、AAS是解题的关键.
13.2<AD<4
【分析】此题要倍长中线,再连接,构造全等三角形.根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
【详解】解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系定理:6-2<AE<6+2,
∴2<AD<4,
故AD的取值范围为2<AD<4.
【点睛】本题主要考查对全等三角形的性质和判定,三角形的三边关系定理等知识点的理解和掌握,能推出6-2<AE<6+2是解此题的关键.
14.见解析
【分析】根据判定,然后根据全等三角形的性质求解即可.
【详解】证明:在和中,
,
,
.
【点睛】本题考查三角形全等判定和性质,解题关键是掌握证明三角形全等.
15.见解析
【分析】根据线段的和可得OD=OC,根据SAS证明△AOD≌△BOC即可得证.
【详解】证明:∵ BD=AC,OB=OA
∵BD+ OB=AC+ OA,
即OD=OC
在△AOD与△BOC中,
,
∴△AOD≌△BOC(SAS).
【点睛】本题考查了三角形全等的判定,证明OD=OC是解题的关键.
16.见解析
【分析】先根据平行线的性质证得,再根据线段和求得,然后证明,即可由全等三角形的性质得出结论.
【详解】证明:∵,∴
∵,∴
∴
在与中,
∴
∴
【点睛】本题考查三角形全等的判定和性质,平行线的性质,熟练掌握全等三角形的判定和性质是解题的关键.
17.见解析
【分析】先由条件得出,,从而可以得出,由全等三角形的性质就可以得出结论.
【详解】证明:∵,
∴.
∵,
∴,
即.
在和中,,
∴,
∴.
【点睛】本题考查了全等三角形的判定及性质的运用,解答时得出是关键.
18.见解析
【分析】根据作图步骤作出要求的图形.
【详解】解:①作直线,并确定点在上;
②过点作;
③在上截取;
④在上截取.
⑤连接,则为所求.
如图所示:为所求.
【点睛】本题考查作图 复杂作图,解题的关键是熟练掌握五种基本作图,注意保留作图痕迹.
19.(1)见解析;
(2)见解析.
【分析】(1)由,依据“两只相平行,同位角相等”得到,结合已知根据“”可判定全等;
(2)根据全等三角形的性质得到,依据“同位角相等,两只相平行”可进行求证.
【详解】(1)∵,
,
在和中,
,
(2),
【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
20.见解析
【分析】先利用平行线的性质得到∠B=∠DEF,∠ACB=∠F,再证明BC=EF,然后根据“ASA”可判断△ABC≌△DEF.
【详解】证明:∵AB∥DE,
∴∠B=∠DEF,
∵AC∥DF,
∴∠ACB=∠F,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
【点睛】本题考查了全等三角形的判定:熟练掌握全等三角形的判定方法是解决问题的关键.选用哪一种判定方法,取决于题目中的已知条件.
21.(1)△AED≌△AFD,△DEB≌△DFC,△ABD≌△ACD
(2)见解析
【分析】(1)根据平分可得 ,为边上中线可得 又,可得,根据全等三角形的判定即可证得 ,,;
(2)根据题目条件证明,即可得到,于是可得.
【详解】(1)解:平分,
, ,
为边上中线,
,
,,
,
在 和中,
,
,
,
在和中,
,
,
在和中,
,
,
故所有的全等三角形为 ,,;
(2)解:由(1)可知 ,
,
.
【点睛】本题主要考查全等是三角形的判定与性质,掌握三角形全等的判定是解决问题的关键.
22.见解析
【分析】首先根据ASA可证得△ABF≌△DCE,可得BF=CE,再根据线段的和差,即可证得结论.
【详解】证明:在△ABF与△DCE中
∴△ABF≌△DCE(ASA),
∴BF=CE.
∴BF-EF=CE-EF ,即BE=CF
【点睛】本题考查了全等三角形的判定与性质,熟练掌握和运用全等三角形的判定与性质是解决本题的关键.
23.见解析
【分析】证明即可证明BE=CF.
【详解】证明:∵AB=AC,AD为∠BAC的平分线
∴BD=CD,
∵DE⊥AB,DF⊥AC
∴DE=DF,
在Rt△BDE和Rt△CDF中
,
∴,
∴BE=CF.
【点睛】本题考查了HL证明三角形全等,以及全等三角形的性质,掌握全等三角形的性质与判定是解题的关键.
24.(1)平行四边形(矩形或菱形或正方形或等腰梯形)
(2)①(或);②见解析
【分析】(1)根据等对边四边形的图形的定义,平行四边形,等腰梯形进行解答便可.
(2)①与A相等的角是(或);
②作于G点,作交CD延长线于F点,易证,进而证明,所以,四边形是等对边四边形.
【详解】(1)平行四边形(矩形或菱形或正方形或等腰梯形)
(2)①(或)
证明:∵,,
∴;(同理可证)
②证明:如图,作于G点,作交CD延长线于F点.
∵,BC为公共边,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴四边形BCED是等对边四边形.
【点睛】本题主要考查了全等三角形的性质与判定,新定义,解决本题的关键是理解等对边四边形的定义,把证明BD=CE的问题转化为证明三角形全等的问题.
25.(1)见解析
(2)
【分析】(1)根据等式的性质得∠BAC=∠EAF,再利用SAS证明△BAC≌△EAF即可得出结论;
(2)根据三角形内角和得∠BAE=56°,再由△BAC≌△EAF,得∠F=∠C=24°,最后利用三角形外角的性质得∠FGC=∠FAC+∠F.
【详解】(1)证明:∵∠CAF=∠BAE,
∴∠CAF+∠EAC=∠BAE+∠EAC,
即∠BAC=∠EAF,
在△BAC和△EAF中,
,
∴△BAC≌△EAF(SAS),
∴EF=BC.
(2)解:∵AB=AE,
∴∠B=∠AEB=62°,
∴∠BAE=56°,
∴∠CAF=∠BAE=56°,
∵△BAC≌△EAF,
∴∠F=∠C=24°,
∴∠FGC=∠FAC+∠F=56°+24°=80°.
【点睛】本题主要考查了全等三角形的判定与性质,三角形外角的性质等知识,证明△BAC≌△EAF是解题的关键.
26.(1)见解析
(2)2
【分析】(1)证明得出,即可;
(2)同理可得得出,即可得出结论.
【详解】(1)证明:,
,
在和中
,
(2)解:,
,
在和中
,
【点睛】本题考查全等三角形的判定与性质、垂线定义、等角的余角相等,熟练掌握全等三角形的判定与性质是解答的关键.
27.(1)添加一个角有关的条件为,使得,理由见解析;(2)的度数为.
【分析】(1)根据已知条件,选择SAS原理,可确定添加的角;
(2)利用三角形全等,∠B的度数,可求∠BAC+∠DAE,问题可解.
【详解】(1)添加一个角方面的条件为,使得.
在和中
∵,,,
∴;
(2)在(1)的条件下∵,
∴,
若,,
则,
∴,
∴,
即的度数为.
【点睛】本题考查了三角形全等,熟练掌握全等三角形判定原理和性质是解题的关键.
28.见解析
【详解】试题分析:证明△ABE≌△ACD 即可.
试题解析:法1:
∵AB=AC,
∴∠B=∠C,
∵AD=CE,
∴∠ADE=∠AED,
∴△ABE≌△ACD,
∴BE=CD ,
∴BD=CE,
法2:如图,作AF⊥BC于F,
∵AB=AC,
∴BF=CF,
∵AD=AE,
∴DF=EF,
∴BF-DF=CF-EF,
即BD=CE.
一、单选题
1.(2022秋·广西贺州·八年级统考期末)如图,通过尺规作图得到的依据是( )
A.SSS B.SAS C.ASA D.AAS
2.(2022秋·广西崇左·八年级统考期末)如图,AC与BD相交于点O,∠1=∠2,若用“SAS”说明△ABC≌△BAD,则还需添加的一个条件是( )
A.AD=BC B.∠C=∠D C.AO=BO D.AC=BD
3.(2022秋·广西南宁·八年级统考期末)如图,在中,,是高,能直接判断的依据是( )
A. B. C. D.
4.(2022秋·广西崇左·八年级统考期末)如图,已知,要使,只需增加的一个条件( )
A. B.
C. D.
5.(2022秋·广西梧州·八年级统考期末)在三角形全等判定定理中,下列哪一个不属于三角形全等判定定理简记( )
A. B. C. D.
6.(2022秋·广西河池·八年级统考期末)如图,为测量桃李湖两端AB的距离,南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C,测得∠ACB的度数,在AC的另一侧测得∠ACD=∠ACB,CD=CB,再测得AD的长,就是AB的长.那么判定△ABC≌△ADC的理由是( )
A.SAS B.SSS C.ASA D.AAS
7.(2022秋·广西百色·八年级统考期末)如图为6个边长相等的正方形组成的图形,则∠1+∠2+∠3的大小是( )
A.90° B.120° C.135° D.150°
8.(2022秋·广西梧州·八年级统考期末)如图,在等腰直角三角形中,,点B在直线l上,过A作于D,过C作于E.下列给出四个结论:①;②与互余;③.其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
9.(2022秋·广西贵港·八年级统考期末)如图,在中,点在边上,是边的中点,//,与的延长线交于点,若,,则的长为 .
10.(2022秋·广西桂林·八年级统考期末)如图是由九个边长为1的小正方形拼成的大正方形,图中∠1+∠2+∠3+∠4+∠5的度数为 .
11.(2022秋·广西北海·八年级统考期末)如图,已知,,,则 .
12.(2022秋·广西贺州·八年级统考期末)如图,点B、E、C、F在同一直线上,AB=DE,BE=CF,要使△ABC≌△DEF,需添加的条件是 (添加一个即可).
13.(2022秋·广西河池·八年级统考期末)如图所示,AD是△ABC中BC边上的中线,若AB=2,AC=6,则AD的取值范围是
三、解答题
14.(2022秋·广西河池·八年级统考期末)如图,,.求证:.
15.(2022秋·广西崇左·八年级统考期末)如图,BD=AC,OB=OA,求证:△AOD≌△BOC.
16.(2022秋·广西柳州·八年级统考期末)如图,点B,F,C,E在同一条直线上,,,.求证:.
17.(2022秋·广西贺州·八年级统考期末)如图,点B、F、C、E在同一条直线上,,,求证:.
18.(2022秋·广西贵港·八年级统考期末)尺规作图(只保留作图痕迹,不要求写出作法):
如图,已知线段和,求作,使,,.
19.(2022秋·广西河池·八年级统考期末)如图,已知点B、E、C、F在同一直线上,,,.求证:
(1);
(2).
20.(2022秋·广西梧州·八年级统考期末)已知:点B、E、C、F在一条直线上,AB∥DE,AC∥DF,BE=CF.求证:△ABC≌△DEF.
21.(2022秋·广西百色·八年级校考期末)如图,△ABC中,AD平分∠BAC,AD也是BC边上的中线,过点D作,垂足为点E垂足为点F.
(1)请用全等符号直接写出图中所有的全等三角形;
(2)求证:.
22.(2022秋·广西百色·八年级统考期末)已知:如图,点E和点F在BC上,∠A=∠D,∠B=∠C,AB=DC.求证:BE=CF.
23.(2022秋·广西钦州·八年级统考期末)如图,在△ABC中,AB=AC,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,求证:BE=CF.
24.(2022秋·广西贵港·八年级统考期末)我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
(2)如图,在中,点、分别在、上,与相交于点,若.
①请你写出图中一个与相等的角;
②证明四边形是等对边四边形.
25.(2022秋·广西崇左·八年级统考期末)如图,在和中,点在边上,,,,与交于点.
(1)求证:;
(2)若,,求的度数.
26.(2022秋·广西河池·八年级统考期末)在中,,直线经过点,于,于.
(1)当直线绕点旋转到图(1)的位置时,求证:;
(2)当直线绕点旋转到图(2)的位置时,此时,,求的长度.
27.(2022秋·广西桂林·八年级统考期末)如图,在五边形中,,.
(1)请你添加一个与角有关的条件,使得,并说明理由;
(2)在(1)的条件下,若,,求的度数.
28.(2022秋·广西百色·八年级统考期末)如图,在△ABC中,AB=AC,点,在边上,.求证:.
参考答案:
1.A
【分析】根据作图过程利用可以证明,进而可得结论.
【详解】解:根据作图过程可知,
在和中,
,
∴,
∴(全等三角形的对应角相等).
故选:A.
【点睛】本题考查了全等三角形的判定与性质,解决本题的关键是掌握基本作图方法.
2.D
【分析】根据全等三角形的判定,已知∠1=∠2,AB为公共边,所以可添加AC=BD,根据SAS可证△ABC≌△BAD.
【详解】解:添加AC=BD,理由如下:
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS),
故选:D.
【点睛】此题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
3.C
【分析】根据直角三角形的全等证明即可判断.
【详解】证明:∵AD⊥BC
∴和是直角三角形,
∵,AD=AD(公共边),
所以≌(HL)
故选C
【点睛】本题主要考查直角三角形的全等证明,掌握直角三角形的全等证明方法是解题的关键.
4.C
【分析】结合图形,发现BC=CB是公共边,选择SAS判断即可.
【详解】∵AC=DB,BC=CB,
∴选择SAS判断,
故选C.
【点睛】本题考查了三角形全等的判定定理,熟练掌握定理并结合已知选择适当原理是解题的关键.
5.B
【分析】根据全等三角形的判定定理分析判断即可.
【详解】解:全等三角形的判定定理分别为:
(1)判定定理1:-三条边分别对应相等的两个三角形全等.
(2)判定定理2:-两边及其夹角分别对应相等的两个三角形全等.故C不符合题意;
(3)判定定理3:-两角及其夹边分别对应相等的两个三角形全等;
(4)判定定理4:-两角及其中一个角的对边对应相等的两个三角形全等.故A不符合题意;
(5)判定定理5:-斜边与直角边对应相等的两个直角三角形全等.故D不符合题意.
全等三角形的判定定理不存在.故B符合题意.
故选:B.
【点睛】本题考查了全等三角形的判定,熟记全等三角形的判定方法是解题的关键.注意:、不能判定两个三角形全等.
6.A
【分析】已知条件是∠ACD=∠ACB,CD=CB,AC=AC,据此作出选择.
【详解】解:在△ADC与△ABC中,
.
∴△ADC≌△ABC(SAS).
故选:A.
【点睛】此题考查了全等三角形的应用,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS,做题时注意选择.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
7.C
【分析】标注字母,利用“边角边”判断出和全等,根据全等三角形对应角相等可得(或观察图形得到,然后求出,再判断出,然后计算即可得解.
【详解】解:如图,在和中,
,
,
(或观察图形得到,
,
,
又,
.
故选:C.
【点睛】本题考查了全等图形,网格结构,解题的关键是准确识图判断出全等的三角形.
8.D
【分析】证△ADB≌△BEC即可.
【详解】证明:∵, ,
∴∠ADB=∠BEC=90°,
∴∠BAD+∠ABD=90°,∠BCE+∠CBE=90°,
∵,
∴∠ABD+∠CBE=90°,
∴∠BAD=∠CBE,
∴∠BCE+∠BAD=90°,故②正确;
∵∠BAD=∠CBE,∠ADB=∠BEC=90°,
∴△ADB≌△BEC,
∴,AD=BE,故①正确;
DE=DB+BE=CE+AD,故③正确;
故选:D.
【点睛】本题考查了全等三角形的判定与性质,解题关键是找到并证明全等三角形.
9.1
【分析】由平行线及中点的性质得出, ,,利用全等三角形的判定和性质及线段间的数量关系即可得出结果.
【详解】解:∵,
∴, ,
∵E是AC边的中点,
∴,
在与中,
,
∴,
∴,
∴,
故答案为:1.
【点睛】题目主要考查全等三角形的判定和性质,平行线的性质等,理解题意,熟练掌握运用各个知识点是解题关键.
10.225°
【分析】首先判定△ABC≌△AEF,△ABD≌△AEH,可得∠5=∠BCA,∠4=∠BDA,然后可得∠1+∠5=∠1+∠BCA=90°,∠2+∠4=∠2+∠BDA=90°,即可求得∠1+∠2+∠3+∠4+∠5的值.
【详解】解:如图所示:
在△ABC和△AEF中,
∴△ABC≌△AEF(SAS),
∴∠5=∠BCA,
∴∠1+∠5=∠1+∠BCA=90°,
在Rt△ABD和Rt△AEH中,
∴Rt△ABD≌Rt△AEH(HL),
∴∠4=∠BDA,
∴∠2+∠4=∠2+∠BDA=90°,
∵∠3=45°,
∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°.
故答案为:225°.
【点睛】此题主要考查了全等三角形的判定和性质,关键是掌握全等三角形的性质:全等三角形对应角相等即可求解.
11.50°
【分析】根据题意证明Rt△ABC≌Rt△ADC,得到∠DAC=∠BAC=40°,根据直角三角形两锐角互余计算即可.
【详解】解:在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠DAC=∠BAC=40°,
∴∠DCA=90°-40°=50°,
故答案为:50°.
【点睛】本题考查的是全等三角形的判定和性质,掌握直角三角形全等的判定定理是解题的关键.
12.∠B=∠DEF或AC=DF
【分析】根据题意,可知两个三角形的两条边相等,只需再加上夹角或者另一条边相等即可证明两个三角形全等.
【详解】,
,即,
又∵,
可添加,利用SAS来证明三角形全等,
也可添加,利用SSS来证明三角形全等,
故答案为: 或.
【点睛】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法,即SSS、SAS、ASA、AAS是解题的关键.
13.2<AD<4
【分析】此题要倍长中线,再连接,构造全等三角形.根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
【详解】解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系定理:6-2<AE<6+2,
∴2<AD<4,
故AD的取值范围为2<AD<4.
【点睛】本题主要考查对全等三角形的性质和判定,三角形的三边关系定理等知识点的理解和掌握,能推出6-2<AE<6+2是解此题的关键.
14.见解析
【分析】根据判定,然后根据全等三角形的性质求解即可.
【详解】证明:在和中,
,
,
.
【点睛】本题考查三角形全等判定和性质,解题关键是掌握证明三角形全等.
15.见解析
【分析】根据线段的和可得OD=OC,根据SAS证明△AOD≌△BOC即可得证.
【详解】证明:∵ BD=AC,OB=OA
∵BD+ OB=AC+ OA,
即OD=OC
在△AOD与△BOC中,
,
∴△AOD≌△BOC(SAS).
【点睛】本题考查了三角形全等的判定,证明OD=OC是解题的关键.
16.见解析
【分析】先根据平行线的性质证得,再根据线段和求得,然后证明,即可由全等三角形的性质得出结论.
【详解】证明:∵,∴
∵,∴
∴
在与中,
∴
∴
【点睛】本题考查三角形全等的判定和性质,平行线的性质,熟练掌握全等三角形的判定和性质是解题的关键.
17.见解析
【分析】先由条件得出,,从而可以得出,由全等三角形的性质就可以得出结论.
【详解】证明:∵,
∴.
∵,
∴,
即.
在和中,,
∴,
∴.
【点睛】本题考查了全等三角形的判定及性质的运用,解答时得出是关键.
18.见解析
【分析】根据作图步骤作出要求的图形.
【详解】解:①作直线,并确定点在上;
②过点作;
③在上截取;
④在上截取.
⑤连接,则为所求.
如图所示:为所求.
【点睛】本题考查作图 复杂作图,解题的关键是熟练掌握五种基本作图,注意保留作图痕迹.
19.(1)见解析;
(2)见解析.
【分析】(1)由,依据“两只相平行,同位角相等”得到,结合已知根据“”可判定全等;
(2)根据全等三角形的性质得到,依据“同位角相等,两只相平行”可进行求证.
【详解】(1)∵,
,
在和中,
,
(2),
【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
20.见解析
【分析】先利用平行线的性质得到∠B=∠DEF,∠ACB=∠F,再证明BC=EF,然后根据“ASA”可判断△ABC≌△DEF.
【详解】证明:∵AB∥DE,
∴∠B=∠DEF,
∵AC∥DF,
∴∠ACB=∠F,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
【点睛】本题考查了全等三角形的判定:熟练掌握全等三角形的判定方法是解决问题的关键.选用哪一种判定方法,取决于题目中的已知条件.
21.(1)△AED≌△AFD,△DEB≌△DFC,△ABD≌△ACD
(2)见解析
【分析】(1)根据平分可得 ,为边上中线可得 又,可得,根据全等三角形的判定即可证得 ,,;
(2)根据题目条件证明,即可得到,于是可得.
【详解】(1)解:平分,
, ,
为边上中线,
,
,,
,
在 和中,
,
,
,
在和中,
,
,
在和中,
,
,
故所有的全等三角形为 ,,;
(2)解:由(1)可知 ,
,
.
【点睛】本题主要考查全等是三角形的判定与性质,掌握三角形全等的判定是解决问题的关键.
22.见解析
【分析】首先根据ASA可证得△ABF≌△DCE,可得BF=CE,再根据线段的和差,即可证得结论.
【详解】证明:在△ABF与△DCE中
∴△ABF≌△DCE(ASA),
∴BF=CE.
∴BF-EF=CE-EF ,即BE=CF
【点睛】本题考查了全等三角形的判定与性质,熟练掌握和运用全等三角形的判定与性质是解决本题的关键.
23.见解析
【分析】证明即可证明BE=CF.
【详解】证明:∵AB=AC,AD为∠BAC的平分线
∴BD=CD,
∵DE⊥AB,DF⊥AC
∴DE=DF,
在Rt△BDE和Rt△CDF中
,
∴,
∴BE=CF.
【点睛】本题考查了HL证明三角形全等,以及全等三角形的性质,掌握全等三角形的性质与判定是解题的关键.
24.(1)平行四边形(矩形或菱形或正方形或等腰梯形)
(2)①(或);②见解析
【分析】(1)根据等对边四边形的图形的定义,平行四边形,等腰梯形进行解答便可.
(2)①与A相等的角是(或);
②作于G点,作交CD延长线于F点,易证,进而证明,所以,四边形是等对边四边形.
【详解】(1)平行四边形(矩形或菱形或正方形或等腰梯形)
(2)①(或)
证明:∵,,
∴;(同理可证)
②证明:如图,作于G点,作交CD延长线于F点.
∵,BC为公共边,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴四边形BCED是等对边四边形.
【点睛】本题主要考查了全等三角形的性质与判定,新定义,解决本题的关键是理解等对边四边形的定义,把证明BD=CE的问题转化为证明三角形全等的问题.
25.(1)见解析
(2)
【分析】(1)根据等式的性质得∠BAC=∠EAF,再利用SAS证明△BAC≌△EAF即可得出结论;
(2)根据三角形内角和得∠BAE=56°,再由△BAC≌△EAF,得∠F=∠C=24°,最后利用三角形外角的性质得∠FGC=∠FAC+∠F.
【详解】(1)证明:∵∠CAF=∠BAE,
∴∠CAF+∠EAC=∠BAE+∠EAC,
即∠BAC=∠EAF,
在△BAC和△EAF中,
,
∴△BAC≌△EAF(SAS),
∴EF=BC.
(2)解:∵AB=AE,
∴∠B=∠AEB=62°,
∴∠BAE=56°,
∴∠CAF=∠BAE=56°,
∵△BAC≌△EAF,
∴∠F=∠C=24°,
∴∠FGC=∠FAC+∠F=56°+24°=80°.
【点睛】本题主要考查了全等三角形的判定与性质,三角形外角的性质等知识,证明△BAC≌△EAF是解题的关键.
26.(1)见解析
(2)2
【分析】(1)证明得出,即可;
(2)同理可得得出,即可得出结论.
【详解】(1)证明:,
,
在和中
,
(2)解:,
,
在和中
,
【点睛】本题考查全等三角形的判定与性质、垂线定义、等角的余角相等,熟练掌握全等三角形的判定与性质是解答的关键.
27.(1)添加一个角有关的条件为,使得,理由见解析;(2)的度数为.
【分析】(1)根据已知条件,选择SAS原理,可确定添加的角;
(2)利用三角形全等,∠B的度数,可求∠BAC+∠DAE,问题可解.
【详解】(1)添加一个角方面的条件为,使得.
在和中
∵,,,
∴;
(2)在(1)的条件下∵,
∴,
若,,
则,
∴,
∴,
即的度数为.
【点睛】本题考查了三角形全等,熟练掌握全等三角形判定原理和性质是解题的关键.
28.见解析
【详解】试题分析:证明△ABE≌△ACD 即可.
试题解析:法1:
∵AB=AC,
∴∠B=∠C,
∵AD=CE,
∴∠ADE=∠AED,
∴△ABE≌△ACD,
∴BE=CD ,
∴BD=CE,
法2:如图,作AF⊥BC于F,
∵AB=AC,
∴BF=CF,
∵AD=AE,
∴DF=EF,
∴BF-DF=CF-EF,
即BD=CE.
