12.3 角的平分线的性质 同步练习(含解析)2022-2023学年上学期广西各地八年级数学期末试题选编
文档属性
| 名称 | 12.3 角的平分线的性质 同步练习(含解析)2022-2023学年上学期广西各地八年级数学期末试题选编 |  | |
| 格式 | docx | ||
| 文件大小 | 818.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 16:03:14 | ||
图片预览




文档简介
12.3 角的平分线的性质
一、单选题
1.(2022秋·广西河池·八年级统考期末)如图,的三边,,长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( ).
A. B. C. D.
2.(2022秋·广西河池·八年级统考期末)如图,是的平分线上一点,于,于,若,则的长为( )
A.1 B.2 C.4 D.8
3.(2022秋·广西北海·八年级统考期末)如图,平分,垂直于E,,,则的面积为( )
A.7 B.8 C.9 D.10
4.(2022秋·广西崇左·八年级统考期末)已知BG是的平分线,点D为BG上任意一点,且于点E,于点F,,则DE的长度是( ).
A.3 B.6 C.8 D.9
5.(2022秋·广西贺州·八年级统考期末)如图,已知在四边形ABCD中,DE⊥BC,BD平分∠ABC,AB=6,DE=4,则△ABD的面积是( )
A.24 B.18 C.12 D.6
6.(2022秋·广西来宾·八年级统考期末)如图,在中,平分,交于点D,,垂足为点E,若,则的长为( )
A. B.1 C.2 D.6
7.(2022秋·广西贺州·八年级统考期末)下列命题中,是假命题的是( )
A.内错角相等 B.对顶角相等
C.两点之间线段最短 D.角平分线上的点到这个角的两边的距离相等
8.(2022秋·广西贺州·八年级统考期末)如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
A.2cm B.3cm C.4cm D.5cm
9.(2022秋·广西玉林·八年级统考期末)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
10.(2022秋·广西柳州·八年级统考期末)在中,,的角平分线交于点,则点到的距离是( )
A.2 B.3 C.4 D.5
11.(2022秋·广西桂林·八年级统考期末)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC长是( )
A.3 B.4 C.5 D.6
12.(2022秋·广西玉林·八年级统考期末)如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
13.(2022秋·广西贵港·八年级统考期末)如图,已知的周长是,和的角平分线交于点O,于点D,若,则的面积是( )
A. B. C. D.
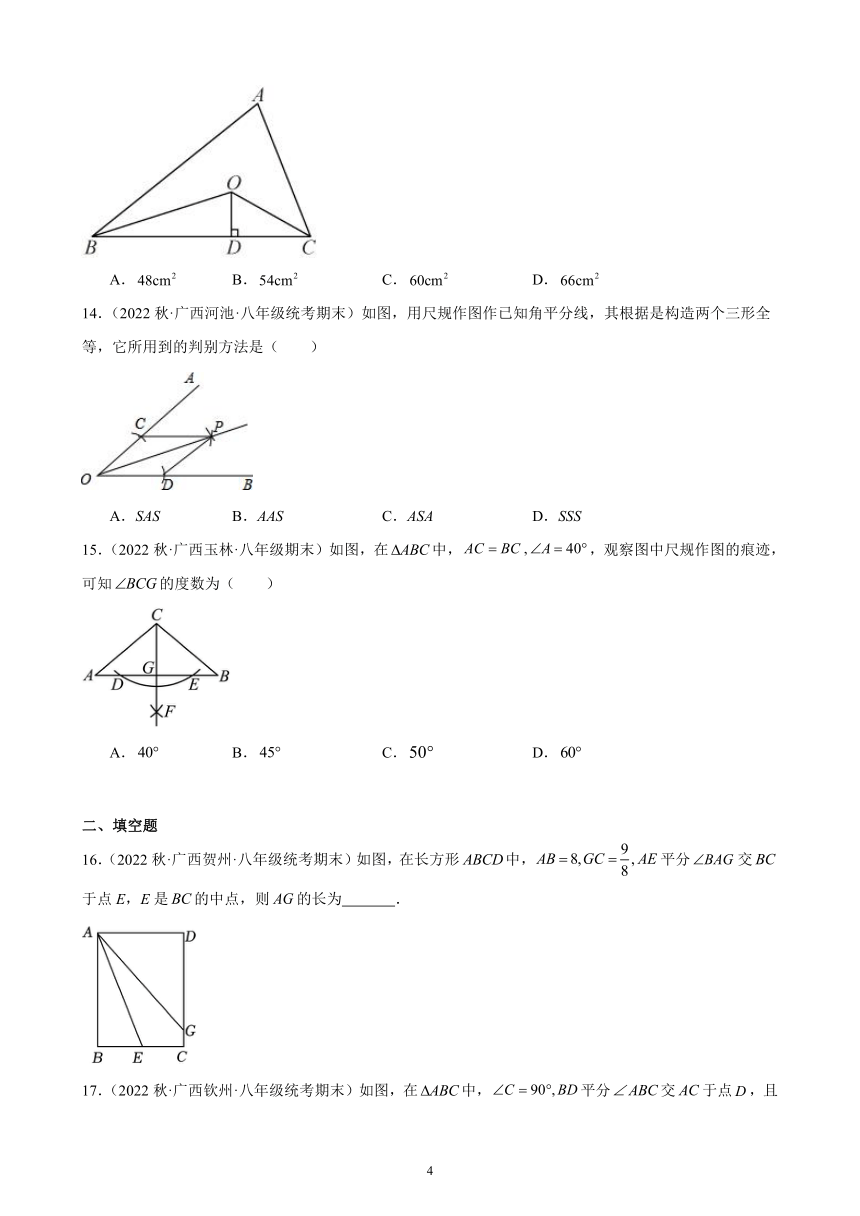
14.(2022秋·广西河池·八年级统考期末)如图,用尺规作图作已知角平分线,其根据是构造两个三形全等,它所用到的判别方法是( )
A.SAS B.AAS C.ASA D.SSS
15.(2022秋·广西玉林·八年级期末)如图,在中,,观察图中尺规作图的痕迹,可知的度数为( )
A. B. C. D.
二、填空题
16.(2022秋·广西贺州·八年级统考期末)如图,在长方形中,平分交于点E,E是的中点,则的长为 .
17.(2022秋·广西钦州·八年级统考期末)如图,在中,平分交于点,且,则的面积为 .
18.(2022秋·广西来宾·八年级统考期末)在平面直角坐标系中,在轴,轴上分别截取,再分别以点,为圆心,以大于长为半径画弧,两弧交于点,若点的坐标为,则的值是 .
19.(2022秋·广西钦州·八年级统考期末)如图,已知△ABC的周长是18,∠ABC和∠ACB的角平分线交于点O,于点D,若OD=3,则△ABC的面积是 .
20.(2022秋·广西崇左·八年级统考期末)△ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于D,ABC的面积18,AB=6,AC=8,OD=2,则BC的长是 .
三、解答题
21.(2022秋·广西贺州·八年级统考期末)如图,平行四边形ABCD中,AE=CE.
(1)用尺规或只用无刻度的直尺作出的角平分线,保留作图痕迹,不需要写作法.
(2)设的角平分线交边AD于点F,连接CF,求证:四边形AECF为菱形.
22.(2022秋·广西梧州·八年级统考期末)已知、分别是内角和外角平分线,它们的交点为,过点D作,垂足为F点,作,垂足为E点,连接.求证:.
23.(2022秋·广西来宾·八年级统考期末)如图,已知是的角平分线,且为的中点,,.
(1)写出图中所有的全等三角形;
(2)求证:.
24.(2022秋·广西崇左·八年级统考期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
25.(2022秋·广西百色·八年级统考期末)如图,在△ABC中,AC=BC,∠C=90 ,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.
26.(2022秋·广西贺州·八年级统考期末)如图,,,求证:平分.
27.(2022秋·广西北海·八年级统考期末) 已知:如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF;求证:AD平分∠BAC.
28.(2022秋·广西钦州·八年级统考期末)如图,四边形ABCD是矩形,求:
(1)作∠ABC的角平分线,交AD于点E,交CD的延长线于点F;(要求:尺规作图,不写作法,保留作图痕迹,写出结论)
(2)在(1)作图中,若E是AD的中点,求证:.
29.(2022秋·广西来宾·八年级统考期末)如图,已知.
(1)按下面的步骤,利用尺规作出的平分线:①以为圆心,任意长为半径作弧,交,于点,;②分别以,为圆心,大于的长为半径作弧,两弧在内交于点;③作射线,则就是的平分线;(保留作图痕迹,标上相应字母)
(2)根据(1)的作图方法证明
30.(2022秋·广西河池·八年级统考期末)已知:如图,在△ABC中,∠A=30°,∠B=60°.
(1)作∠B的平分线BD,交AC于点D;
(2)作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(3)连接DE,求证:△ADE≌△BDE.
参考答案:
1.C
【分析】过点分别作,,的垂线,可得,从而可证,即可求解.
【详解】解:如图,过点分别作,,的垂线,垂足分别为点,,,
由角平分线的性质定理得:,
的三边,,长分别是20,30,40,
.
故选:C.
【点睛】本题考查了角平分线的性质定理,掌握定理是解题的关键.
2.C
【分析】先根据角平分线的性质得出PE=PF,再利用HL证明Rt△APE≌Rt△APF,根据全等三角形的对应边相等即可得到AE=AF=4.
【详解】解:∵P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,
∴PE=PF,∠AEP=∠AFP=90°,
在Rt△APE与Rt△APF中,,
∴Rt△APE≌Rt△APF(HL),
∴AE=AF=4.
故选:C.
【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.同时考查了全等三角形的判定与性质.
3.C
【分析】过点D作DF⊥BA交BA延长于F,利用角平分线的性质求得DF=DE=3,即可用三角形面积公式求解.
【详解】解:如图,过点D作DF⊥BA交BA延长于F,
∵平分,垂直于E,DF⊥BA交BA延长于F,
∴DF=DE=3,
∴S△ABD==×6×3=9,
故选:C.
【点睛】本题考查角平分线的性质,三角形的面积,熟练掌握角平分线的性质是解题的关键.
4.A
【分析】根据角平分线的性质,角平分线上的点到角两边的距离相等,即可得出结论.
【详解】解:∵BG是∠ABC的平分线
且DEAB,DFBC
∴DE=DF=3
故选:A.
【点睛】本题考查角平分线的性质,解题的关键是熟练掌握角平分线的性质.
5.C
【分析】过点D作DF⊥AB交AB的延长线于点F,由角平分线的性质得出DF=DE,可得出△ABD的面积.
【详解】解:如图,过点D作DF⊥AB交AB的延长线于点F,
∵BD平分∠ABC,DF⊥AB,DE⊥BC,
∴DE=DF=4,
∴
故选:C.
【点睛】本题考查了角平分线的性质熟练掌握性质是解题的关键.
6.B
【分析】根据∠B=90°,AD平分∠BAC,DE⊥AC,再根据角平分线的性质得到DE=BD=1.
【详解】∵,∴,又∵平分,,∴由角平分线的性质得.
故选:B
【点睛】本题主要考查了角平分线的性质,灵活运用角平分线的性质处理问题.
7.A
【分析】根据平行线的性质,对顶角的性质,线段公理,角平分线的性质定理逐一判断选项,即可得到答案.
【详解】A、内错角相等,是假命题,
B、对顶角相等,是真命题,
C、两点之间线段最短,是真命题,
D、角平分线上的点到这个角的两边的距离相等,是真命题.
故选:A.
【点睛】本题主要考查真假命题,掌握平行线的性质,对顶角的性质,线段公理,角平分线的性质定理,是解题的关键.
8.B
【分析】直接利用角平分线的性质得出DE=EC,进而得出答案.
【详解】解:∵△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,
∴EC=DE,
∴AE+DE=AE+EC=3cm.
故选:B.
【点睛】此题主要考查了角平分线的性质,得出EC=DE是解题关键.
9.C
【详解】如图,过点E作EF⊥BC交BC于点F,根据角平分线的性质可得DE=EF=2,所以△BCE的面积等于,
故选:C.
10.B
【分析】过D作DE⊥AB于E,得出DE的长度是D到AB边的距离,根据角平分线性质得出ED=DC,代入求出即可.
【详解】解:过点D作DE⊥AB于E,则DE的长是点D到AB的距离
∵AD是∠BAC的角平分线,∠C=,DE⊥AB
∴DE=DC(角平分线上的点到角两边的距离相等)
∵BC=7,BD=4
∴DC=BC-BD=3
∴DE=3
故点D到AB的距离是3.
故选B.
【点睛】本题考查了角平分线的性质.
11.B
【详解】如图,作DF⊥AC交AC于点F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∴S△ABC=S△ADC+S△ADB=AC·DF+AB·DE=DE(AC+AB)=9,
∴×2×(AC+5)=9,
∴AC=4
故选:B.
12.B
【详解】试题分析:已知OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,根据角平分线的性质可得PC=PD,A正确;在Rt△OCP与Rt△ODP中,OP=OP,PC=PD,由HL可判定△OCP≌△ODP,根据全等三角形的性质可得∠CPO=∠DPO,OC=OD,故C、D正确.不能得出∠CPD=∠DOP,故B错误.故答案选B.
考点:角平分线的性质;全等三角形的判定及性质.
13.B
【分析】过点O作OE⊥AB于点E,OF⊥AC于点F,根据角平分线的性质定理可得OD=OE=OF=3cm,再由,即可求解.
【详解】解∶如图,过点O作OE⊥AB于点E,OF⊥AC于点F,
∵和的角平分线交于点O,,
∴OD=OE,OD=OF,
∴OD=OE=OF=3cm,
∵的周长是,
∴AB+BC+AC=36cm,
∵,
∴.
故选:B
【点睛】本题主要考查了角平分线的性质,熟练掌握角平分线上点到角两边的距离是解题的关键.
14.D
【分析】根据作图过程可知:OC=OD,PC=PD,又OP=OP,从而利用SSS判断出△OCP≌△ODP,根据全等三角形的对应角相等得出∠COP=∠DOP,即OP平分∠AOB,从而得出答案.
【详解】解:由画法得OC=OD,PC=PD,
而OP=OP,
所以△OCP≌△ODP(SSS),
所以∠COP=∠DOP,
即OP平分∠AOB.
故答案为:D.
【点睛】本题考查了用尺规作图作已知角平分线,三角形全等的判定,用尺规作图作已知角平分线,三角形全等的判定掌握是解题的关键.
15.C
【分析】利用等腰三角形的性质和基本作图得到,则平分,利用和三角形内角和计算出,从而得到的度数.
【详解】由作法得,
∵,
∴平分,,
∵,
∴.
故选C.
【点睛】本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了等腰三角形的性质.
16.
【分析】过E作于H,连接,根据角平分线的性质得到,证明,得到,再证明,得到,即可求出.
【详解】解:过E作于H,连接,
∵四边形是矩形,
∴,
∵平分交于点E,
∴,
在与中,
,
∴,
∴,
∵E是的中点,
∴,
∴,
在与中,
,
∴,
∴,
∴,
故答案为:.
【点睛】此题考查了角平分线的性质定理,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.
17.
【分析】如图,过点D作DE⊥AB于E,根据角平分线达到性质可得DE=CD,利用三角形面积公式即可得答案.
【详解】如图,过点D作DE⊥AB于E,
∵,BD平分交于点,
∴DE=CD=3,
∵AB=10,
∴S△ABD=AB·DE=×10×3=15.
故答案为:15
【点睛】本题考查角平分线的性质,角平分线上的点,到角两边的距离相等;熟练掌握角平分线的性质是解题关键.
18.±2
【分析】先由作图得出点P在∠AOB的平分线上,再根据象限角平分线上点的坐标特征横纵坐标绝对值相等,得出|a|=2,求解即可.
【详解】解:由作图可知,点P在∠AOB的平分线上,
∵OA在x轴上,OB在y轴上,点的坐标为
∴|a|=2,
∴a=±2,
故答案为:±2.
【点睛】本题考查基本作图-作角平分线,象限角平分线上点的坐标特征,熟练掌握作角平分线、象限角平分线上点的坐标特征横纵坐标绝对值相等是解题的关键.
19.27
【分析】过点作于,于,连接,如图,根据角平分线的性质得,,由于,所以根据三角形的面积公式可计算出的面积.
【详解】解:过点作于,于,连接,如图,
平分,,,
,
同理可得,
,
的周长是18,
.
故答案为:.
【点睛】本题考查了角平分线的性质,三角形面积公式,解题的关键是掌握角的平分线上的点到角的两边的距离相等.
20.4
【详解】试题分析:过点O作OE⊥AB,OF⊥AC,利用角平分线的性质可知OE=OF=OD=2,利用三角形的面积公式可解得结果.
解:过点O作OE⊥AB,OF⊥AC,连接AO,
∵OB,OD为∠ABC和∠ACB的平分线,OD⊥BC,
∴OE=OF=OD=2,
∵S△ABC=S△ABO+S△BOC+S△AOC
=
=
∵△ABC的面积18,
∴=18,
解得:BC=4,
故答案为4.
考点:角平分线的性质.
21.(1)见详解;(2)见解析.
【分析】(1)只用无刻度直尺作图过程如下:①连接AC、BD交于点O,②连接EO,EO为∠AEC的角平分线;
(2)先根据AF=EC,AF∥CE,判定四边形AECF是平行四边形,再根据AE=EC,即可得出平行四边形AECF是菱形.
【详解】解:(1)如图所示,EO为∠AEC的角平分线;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFE=∠FEC,
又∵∠AEF=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF,
∴AF=EC,
∴四边形AECF是平行四边形,
又∵AE=EC,
∴平行四边形AECF是菱形.
【点睛】本题主要考查了平行四边形的性质以及菱形的判定,解题时注意:一组邻边相等的平行四边形是菱形.
22.见解析
【分析】过点D作于点G,利用角平分线的性质,得到,,再证明,利用全等三角形对应边相等,即可得证.
【详解】证明:如图,过点D作于点G,
∵平分,,
∴,
∵平分,,
∴,
∴,
在和中,
,
∴,
∴.
【点睛】本题考查角平分线的性质,以及全等三角形判定和性质.熟练掌握角平分线上的点到角两边的距离相等,是解题的关键.
23.(1)△ADE≌△ADF,△BDE≌△CDF,△ABD≌△ACD
(2)见解析
【分析】(1)先由角平分线性质证DE=DF,则可由HL证Rt△ADE≌Rt△ADF,得AE=AF,再证Rt△BDE≌Rt△CDF,得BE=CF,从而得AB=AC,即可用SSS证△ABD≌△ACD,即可得出答案.
【详解】(1)解:∵是的角平分线,,,
∴DE=DF,∠AED=∠AFD=90°,
∵AD=AD,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∵为的中点,
∴BD=CD,
∵DE=DF,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF,
∴AB=AC,
∵AD=AD,BD=CD,
∴△ABD≌△ACD(SSS),
∴图中所有的全等三角形有:△ADE≌△ADF,△BDE≌△CDF,△ABD≌△ACD;
(2)证明:∵是的角平分线,,,
∴DE=DF,∠BED=∠CFD=90°,
∵为的中点,
∴BD=CD,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
【点睛】本题考查全等三角形的判定与性质,角平分线的性质,熟练掌握全等三角形的判定与性质与角平分线的性质是解题的关键.
24.(1)见解析
(2)AF+BE=AE,理由见解析
【分析】(1)根据角平分线的性质得到DC=DE,根据直角三角形全等的判定定理得到Rt△DCF≌Rt△DEB,根据全等三角形的性质定理得到答案;
(2)根据全等三角形的性质定理得到AC=AE,根据(1)的结论得到答案.
【详解】(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB,
∴CF=EB;
(2)解:AF+BE=AE.理由如下:
∵Rt△DCF≌Rt△DEB,
∴DC=DE,
∴Rt△DCA≌Rt△DEA(HL),
∴AC=AE,
∴AF+FC=AE,
即AF+BE=AE.
【点睛】本题考查的是角平分线的性质和三角形全等的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键,注意直角三角形全等的判定方法.
25.见解析
【分析】根据已知AC=BC,∠C=90,可得出DE=EB,再利用AD是△ABC的角平分线,DE⊥AB,可证明△ACD≌△AED,然后利用全等三角形的对应边相等和等量代换即可证明AB=AC+CD.
【详解】证明:∵在△ABC中,AC=BC,∠C=90°,
∴∠ABC=45°,
又∵DE⊥AB,垂足为E,
∴∠B=∠EDB=45°,
∴DE=EB,
又∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴DE=CD.
在Rt△ACD与Rt△AED中,
∵,
∴△ACD≌△AED,
∴AC=AE,CD=DE,
∴AB=AE+EB=AC+CD.
【点睛】此题考查学生对等腰直角三角形的判定与性质,全等三角形的判定与性质,角平分线的性质等知识点的理解和掌握,证明此题的关键是证明△ACD≌△AED,此题难度不大,属于基础题.
26.见解析
【分析】过点D作于点E,于点F,证明,得出,
【详解】证明:过点D作于点E,于点F,如图所示:
∴,
∵,,
∴,
在和中,
∴,
∴,
∴点D在的角平分线上,
∴平分.
【点睛】本题主要考查了角平分线的判定,三角形全等的判定和性质,余角的性质,解题的关键是作出辅助线,构造全等三角形,证明.
27.见解析
【分析】根据已知条件证明△BDE≌△CDF,得到DE=DF,再根据角平分线的判定定理即可得到结论.
【详解】证明:∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
【点睛】此题考查三角形全等的判定及性质,角平分线的判定定理,正确理解题意证明∴Rt△BDE≌Rt△CDF是解题的关键.
28.(1)见解析
(2)见解析
【分析】(1)以点B为圆心,以小于长为半径画弧,分别交AB、BC于两点,再分别以这两点为圆心,以这两点间距离的一半为半径画弧,交于一点,连接这点与B得到BF,即可求解;
(2)由E是AD的中点得到,由矩形的性质得到,根据“ASA”即可求解.
【详解】(1)解:根据角平分线作法画图如下,射线BF为所求作的角平分线,
(2)证明:∵E是AD的中点,
∴AE=DE .
∵四边形ABCD是矩形,
∴∠A=∠ADC=∠ADF=90°,
在△ABE和△DFE中
∴.
【点睛】本题主要考查了全等三角形的判定,作图-基本作图:熟练掌握角平分线的作法是解决问题的关键.
29.(1)见解析
(2)见解析
【分析】(1)按步骤尺规作图即可;
(2)如图:连结、,由(1)作图可得、,然后再运用SSS证明≌,最后运用全等三角形的性质即可证明结论.
【详解】(1)解:如图所示,即为所求的平分线.
(2)解:连结、
由(1)作图可知,
在和中,
,,(公共边)
∴
∴(全等三角形对应角相等).
【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点,掌握尺规作图作角平分线成为解答本题的关键.
30.(1)作图见解析;(2)作图见解析;(3)证明见解析.
【详解】试题分析:(1)①以B为圆心,任意长为半径画弧,交AB、BC于F、N,再以F、N为圆心,大于FN长为半径画弧,两弧交于点M,过B、M画射线,交AC于D,线段BD就是∠B的平分线;
(2)分别以A、B为圆心,大于AB长为半径画弧,两弧交于X、Y,过X、Y画直线与AB交于点E,点E就是AB的中点;
(3)首先根据角平分线的性质可得∠ABD的度数,进而得到∠ABD=∠A,根据等角对等边可得AD=BD,再加上条件AE=BE,ED=ED,即可利用SSS证明△ADE≌△BDE.
试题解析:(1)作出∠B的平分线BD;
(2)作出AB的中点E.
(3)证明:
∵∠ABD=×60°=30°,∠A=30°,
∴∠ABD=∠A,
∴AD=BD,
在△ADE和△BDE中,
∴△ADE≌△BDE(SSS).
一、单选题
1.(2022秋·广西河池·八年级统考期末)如图,的三边,,长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( ).
A. B. C. D.
2.(2022秋·广西河池·八年级统考期末)如图,是的平分线上一点,于,于,若,则的长为( )
A.1 B.2 C.4 D.8
3.(2022秋·广西北海·八年级统考期末)如图,平分,垂直于E,,,则的面积为( )
A.7 B.8 C.9 D.10
4.(2022秋·广西崇左·八年级统考期末)已知BG是的平分线,点D为BG上任意一点,且于点E,于点F,,则DE的长度是( ).
A.3 B.6 C.8 D.9
5.(2022秋·广西贺州·八年级统考期末)如图,已知在四边形ABCD中,DE⊥BC,BD平分∠ABC,AB=6,DE=4,则△ABD的面积是( )
A.24 B.18 C.12 D.6
6.(2022秋·广西来宾·八年级统考期末)如图,在中,平分,交于点D,,垂足为点E,若,则的长为( )
A. B.1 C.2 D.6
7.(2022秋·广西贺州·八年级统考期末)下列命题中,是假命题的是( )
A.内错角相等 B.对顶角相等
C.两点之间线段最短 D.角平分线上的点到这个角的两边的距离相等
8.(2022秋·广西贺州·八年级统考期末)如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
A.2cm B.3cm C.4cm D.5cm
9.(2022秋·广西玉林·八年级统考期末)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
10.(2022秋·广西柳州·八年级统考期末)在中,,的角平分线交于点,则点到的距离是( )
A.2 B.3 C.4 D.5
11.(2022秋·广西桂林·八年级统考期末)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC长是( )
A.3 B.4 C.5 D.6
12.(2022秋·广西玉林·八年级统考期末)如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
13.(2022秋·广西贵港·八年级统考期末)如图,已知的周长是,和的角平分线交于点O,于点D,若,则的面积是( )
A. B. C. D.
14.(2022秋·广西河池·八年级统考期末)如图,用尺规作图作已知角平分线,其根据是构造两个三形全等,它所用到的判别方法是( )
A.SAS B.AAS C.ASA D.SSS
15.(2022秋·广西玉林·八年级期末)如图,在中,,观察图中尺规作图的痕迹,可知的度数为( )
A. B. C. D.
二、填空题
16.(2022秋·广西贺州·八年级统考期末)如图,在长方形中,平分交于点E,E是的中点,则的长为 .
17.(2022秋·广西钦州·八年级统考期末)如图,在中,平分交于点,且,则的面积为 .
18.(2022秋·广西来宾·八年级统考期末)在平面直角坐标系中,在轴,轴上分别截取,再分别以点,为圆心,以大于长为半径画弧,两弧交于点,若点的坐标为,则的值是 .
19.(2022秋·广西钦州·八年级统考期末)如图,已知△ABC的周长是18,∠ABC和∠ACB的角平分线交于点O,于点D,若OD=3,则△ABC的面积是 .
20.(2022秋·广西崇左·八年级统考期末)△ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于D,ABC的面积18,AB=6,AC=8,OD=2,则BC的长是 .
三、解答题
21.(2022秋·广西贺州·八年级统考期末)如图,平行四边形ABCD中,AE=CE.
(1)用尺规或只用无刻度的直尺作出的角平分线,保留作图痕迹,不需要写作法.
(2)设的角平分线交边AD于点F,连接CF,求证:四边形AECF为菱形.
22.(2022秋·广西梧州·八年级统考期末)已知、分别是内角和外角平分线,它们的交点为,过点D作,垂足为F点,作,垂足为E点,连接.求证:.
23.(2022秋·广西来宾·八年级统考期末)如图,已知是的角平分线,且为的中点,,.
(1)写出图中所有的全等三角形;
(2)求证:.
24.(2022秋·广西崇左·八年级统考期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
25.(2022秋·广西百色·八年级统考期末)如图,在△ABC中,AC=BC,∠C=90 ,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.
26.(2022秋·广西贺州·八年级统考期末)如图,,,求证:平分.
27.(2022秋·广西北海·八年级统考期末) 已知:如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF;求证:AD平分∠BAC.
28.(2022秋·广西钦州·八年级统考期末)如图,四边形ABCD是矩形,求:
(1)作∠ABC的角平分线,交AD于点E,交CD的延长线于点F;(要求:尺规作图,不写作法,保留作图痕迹,写出结论)
(2)在(1)作图中,若E是AD的中点,求证:.
29.(2022秋·广西来宾·八年级统考期末)如图,已知.
(1)按下面的步骤,利用尺规作出的平分线:①以为圆心,任意长为半径作弧,交,于点,;②分别以,为圆心,大于的长为半径作弧,两弧在内交于点;③作射线,则就是的平分线;(保留作图痕迹,标上相应字母)
(2)根据(1)的作图方法证明
30.(2022秋·广西河池·八年级统考期末)已知:如图,在△ABC中,∠A=30°,∠B=60°.
(1)作∠B的平分线BD,交AC于点D;
(2)作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(3)连接DE,求证:△ADE≌△BDE.
参考答案:
1.C
【分析】过点分别作,,的垂线,可得,从而可证,即可求解.
【详解】解:如图,过点分别作,,的垂线,垂足分别为点,,,
由角平分线的性质定理得:,
的三边,,长分别是20,30,40,
.
故选:C.
【点睛】本题考查了角平分线的性质定理,掌握定理是解题的关键.
2.C
【分析】先根据角平分线的性质得出PE=PF,再利用HL证明Rt△APE≌Rt△APF,根据全等三角形的对应边相等即可得到AE=AF=4.
【详解】解:∵P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,
∴PE=PF,∠AEP=∠AFP=90°,
在Rt△APE与Rt△APF中,,
∴Rt△APE≌Rt△APF(HL),
∴AE=AF=4.
故选:C.
【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.同时考查了全等三角形的判定与性质.
3.C
【分析】过点D作DF⊥BA交BA延长于F,利用角平分线的性质求得DF=DE=3,即可用三角形面积公式求解.
【详解】解:如图,过点D作DF⊥BA交BA延长于F,
∵平分,垂直于E,DF⊥BA交BA延长于F,
∴DF=DE=3,
∴S△ABD==×6×3=9,
故选:C.
【点睛】本题考查角平分线的性质,三角形的面积,熟练掌握角平分线的性质是解题的关键.
4.A
【分析】根据角平分线的性质,角平分线上的点到角两边的距离相等,即可得出结论.
【详解】解:∵BG是∠ABC的平分线
且DEAB,DFBC
∴DE=DF=3
故选:A.
【点睛】本题考查角平分线的性质,解题的关键是熟练掌握角平分线的性质.
5.C
【分析】过点D作DF⊥AB交AB的延长线于点F,由角平分线的性质得出DF=DE,可得出△ABD的面积.
【详解】解:如图,过点D作DF⊥AB交AB的延长线于点F,
∵BD平分∠ABC,DF⊥AB,DE⊥BC,
∴DE=DF=4,
∴
故选:C.
【点睛】本题考查了角平分线的性质熟练掌握性质是解题的关键.
6.B
【分析】根据∠B=90°,AD平分∠BAC,DE⊥AC,再根据角平分线的性质得到DE=BD=1.
【详解】∵,∴,又∵平分,,∴由角平分线的性质得.
故选:B
【点睛】本题主要考查了角平分线的性质,灵活运用角平分线的性质处理问题.
7.A
【分析】根据平行线的性质,对顶角的性质,线段公理,角平分线的性质定理逐一判断选项,即可得到答案.
【详解】A、内错角相等,是假命题,
B、对顶角相等,是真命题,
C、两点之间线段最短,是真命题,
D、角平分线上的点到这个角的两边的距离相等,是真命题.
故选:A.
【点睛】本题主要考查真假命题,掌握平行线的性质,对顶角的性质,线段公理,角平分线的性质定理,是解题的关键.
8.B
【分析】直接利用角平分线的性质得出DE=EC,进而得出答案.
【详解】解:∵△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,
∴EC=DE,
∴AE+DE=AE+EC=3cm.
故选:B.
【点睛】此题主要考查了角平分线的性质,得出EC=DE是解题关键.
9.C
【详解】如图,过点E作EF⊥BC交BC于点F,根据角平分线的性质可得DE=EF=2,所以△BCE的面积等于,
故选:C.
10.B
【分析】过D作DE⊥AB于E,得出DE的长度是D到AB边的距离,根据角平分线性质得出ED=DC,代入求出即可.
【详解】解:过点D作DE⊥AB于E,则DE的长是点D到AB的距离
∵AD是∠BAC的角平分线,∠C=,DE⊥AB
∴DE=DC(角平分线上的点到角两边的距离相等)
∵BC=7,BD=4
∴DC=BC-BD=3
∴DE=3
故点D到AB的距离是3.
故选B.
【点睛】本题考查了角平分线的性质.
11.B
【详解】如图,作DF⊥AC交AC于点F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∴S△ABC=S△ADC+S△ADB=AC·DF+AB·DE=DE(AC+AB)=9,
∴×2×(AC+5)=9,
∴AC=4
故选:B.
12.B
【详解】试题分析:已知OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,根据角平分线的性质可得PC=PD,A正确;在Rt△OCP与Rt△ODP中,OP=OP,PC=PD,由HL可判定△OCP≌△ODP,根据全等三角形的性质可得∠CPO=∠DPO,OC=OD,故C、D正确.不能得出∠CPD=∠DOP,故B错误.故答案选B.
考点:角平分线的性质;全等三角形的判定及性质.
13.B
【分析】过点O作OE⊥AB于点E,OF⊥AC于点F,根据角平分线的性质定理可得OD=OE=OF=3cm,再由,即可求解.
【详解】解∶如图,过点O作OE⊥AB于点E,OF⊥AC于点F,
∵和的角平分线交于点O,,
∴OD=OE,OD=OF,
∴OD=OE=OF=3cm,
∵的周长是,
∴AB+BC+AC=36cm,
∵,
∴.
故选:B
【点睛】本题主要考查了角平分线的性质,熟练掌握角平分线上点到角两边的距离是解题的关键.
14.D
【分析】根据作图过程可知:OC=OD,PC=PD,又OP=OP,从而利用SSS判断出△OCP≌△ODP,根据全等三角形的对应角相等得出∠COP=∠DOP,即OP平分∠AOB,从而得出答案.
【详解】解:由画法得OC=OD,PC=PD,
而OP=OP,
所以△OCP≌△ODP(SSS),
所以∠COP=∠DOP,
即OP平分∠AOB.
故答案为:D.
【点睛】本题考查了用尺规作图作已知角平分线,三角形全等的判定,用尺规作图作已知角平分线,三角形全等的判定掌握是解题的关键.
15.C
【分析】利用等腰三角形的性质和基本作图得到,则平分,利用和三角形内角和计算出,从而得到的度数.
【详解】由作法得,
∵,
∴平分,,
∵,
∴.
故选C.
【点睛】本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了等腰三角形的性质.
16.
【分析】过E作于H,连接,根据角平分线的性质得到,证明,得到,再证明,得到,即可求出.
【详解】解:过E作于H,连接,
∵四边形是矩形,
∴,
∵平分交于点E,
∴,
在与中,
,
∴,
∴,
∵E是的中点,
∴,
∴,
在与中,
,
∴,
∴,
∴,
故答案为:.
【点睛】此题考查了角平分线的性质定理,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.
17.
【分析】如图,过点D作DE⊥AB于E,根据角平分线达到性质可得DE=CD,利用三角形面积公式即可得答案.
【详解】如图,过点D作DE⊥AB于E,
∵,BD平分交于点,
∴DE=CD=3,
∵AB=10,
∴S△ABD=AB·DE=×10×3=15.
故答案为:15
【点睛】本题考查角平分线的性质,角平分线上的点,到角两边的距离相等;熟练掌握角平分线的性质是解题关键.
18.±2
【分析】先由作图得出点P在∠AOB的平分线上,再根据象限角平分线上点的坐标特征横纵坐标绝对值相等,得出|a|=2,求解即可.
【详解】解:由作图可知,点P在∠AOB的平分线上,
∵OA在x轴上,OB在y轴上,点的坐标为
∴|a|=2,
∴a=±2,
故答案为:±2.
【点睛】本题考查基本作图-作角平分线,象限角平分线上点的坐标特征,熟练掌握作角平分线、象限角平分线上点的坐标特征横纵坐标绝对值相等是解题的关键.
19.27
【分析】过点作于,于,连接,如图,根据角平分线的性质得,,由于,所以根据三角形的面积公式可计算出的面积.
【详解】解:过点作于,于,连接,如图,
平分,,,
,
同理可得,
,
的周长是18,
.
故答案为:.
【点睛】本题考查了角平分线的性质,三角形面积公式,解题的关键是掌握角的平分线上的点到角的两边的距离相等.
20.4
【详解】试题分析:过点O作OE⊥AB,OF⊥AC,利用角平分线的性质可知OE=OF=OD=2,利用三角形的面积公式可解得结果.
解:过点O作OE⊥AB,OF⊥AC,连接AO,
∵OB,OD为∠ABC和∠ACB的平分线,OD⊥BC,
∴OE=OF=OD=2,
∵S△ABC=S△ABO+S△BOC+S△AOC
=
=
∵△ABC的面积18,
∴=18,
解得:BC=4,
故答案为4.
考点:角平分线的性质.
21.(1)见详解;(2)见解析.
【分析】(1)只用无刻度直尺作图过程如下:①连接AC、BD交于点O,②连接EO,EO为∠AEC的角平分线;
(2)先根据AF=EC,AF∥CE,判定四边形AECF是平行四边形,再根据AE=EC,即可得出平行四边形AECF是菱形.
【详解】解:(1)如图所示,EO为∠AEC的角平分线;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFE=∠FEC,
又∵∠AEF=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF,
∴AF=EC,
∴四边形AECF是平行四边形,
又∵AE=EC,
∴平行四边形AECF是菱形.
【点睛】本题主要考查了平行四边形的性质以及菱形的判定,解题时注意:一组邻边相等的平行四边形是菱形.
22.见解析
【分析】过点D作于点G,利用角平分线的性质,得到,,再证明,利用全等三角形对应边相等,即可得证.
【详解】证明:如图,过点D作于点G,
∵平分,,
∴,
∵平分,,
∴,
∴,
在和中,
,
∴,
∴.
【点睛】本题考查角平分线的性质,以及全等三角形判定和性质.熟练掌握角平分线上的点到角两边的距离相等,是解题的关键.
23.(1)△ADE≌△ADF,△BDE≌△CDF,△ABD≌△ACD
(2)见解析
【分析】(1)先由角平分线性质证DE=DF,则可由HL证Rt△ADE≌Rt△ADF,得AE=AF,再证Rt△BDE≌Rt△CDF,得BE=CF,从而得AB=AC,即可用SSS证△ABD≌△ACD,即可得出答案.
【详解】(1)解:∵是的角平分线,,,
∴DE=DF,∠AED=∠AFD=90°,
∵AD=AD,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∵为的中点,
∴BD=CD,
∵DE=DF,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF,
∴AB=AC,
∵AD=AD,BD=CD,
∴△ABD≌△ACD(SSS),
∴图中所有的全等三角形有:△ADE≌△ADF,△BDE≌△CDF,△ABD≌△ACD;
(2)证明:∵是的角平分线,,,
∴DE=DF,∠BED=∠CFD=90°,
∵为的中点,
∴BD=CD,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
【点睛】本题考查全等三角形的判定与性质,角平分线的性质,熟练掌握全等三角形的判定与性质与角平分线的性质是解题的关键.
24.(1)见解析
(2)AF+BE=AE,理由见解析
【分析】(1)根据角平分线的性质得到DC=DE,根据直角三角形全等的判定定理得到Rt△DCF≌Rt△DEB,根据全等三角形的性质定理得到答案;
(2)根据全等三角形的性质定理得到AC=AE,根据(1)的结论得到答案.
【详解】(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB,
∴CF=EB;
(2)解:AF+BE=AE.理由如下:
∵Rt△DCF≌Rt△DEB,
∴DC=DE,
∴Rt△DCA≌Rt△DEA(HL),
∴AC=AE,
∴AF+FC=AE,
即AF+BE=AE.
【点睛】本题考查的是角平分线的性质和三角形全等的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键,注意直角三角形全等的判定方法.
25.见解析
【分析】根据已知AC=BC,∠C=90,可得出DE=EB,再利用AD是△ABC的角平分线,DE⊥AB,可证明△ACD≌△AED,然后利用全等三角形的对应边相等和等量代换即可证明AB=AC+CD.
【详解】证明:∵在△ABC中,AC=BC,∠C=90°,
∴∠ABC=45°,
又∵DE⊥AB,垂足为E,
∴∠B=∠EDB=45°,
∴DE=EB,
又∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴DE=CD.
在Rt△ACD与Rt△AED中,
∵,
∴△ACD≌△AED,
∴AC=AE,CD=DE,
∴AB=AE+EB=AC+CD.
【点睛】此题考查学生对等腰直角三角形的判定与性质,全等三角形的判定与性质,角平分线的性质等知识点的理解和掌握,证明此题的关键是证明△ACD≌△AED,此题难度不大,属于基础题.
26.见解析
【分析】过点D作于点E,于点F,证明,得出,
【详解】证明:过点D作于点E,于点F,如图所示:
∴,
∵,,
∴,
在和中,
∴,
∴,
∴点D在的角平分线上,
∴平分.
【点睛】本题主要考查了角平分线的判定,三角形全等的判定和性质,余角的性质,解题的关键是作出辅助线,构造全等三角形,证明.
27.见解析
【分析】根据已知条件证明△BDE≌△CDF,得到DE=DF,再根据角平分线的判定定理即可得到结论.
【详解】证明:∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
【点睛】此题考查三角形全等的判定及性质,角平分线的判定定理,正确理解题意证明∴Rt△BDE≌Rt△CDF是解题的关键.
28.(1)见解析
(2)见解析
【分析】(1)以点B为圆心,以小于长为半径画弧,分别交AB、BC于两点,再分别以这两点为圆心,以这两点间距离的一半为半径画弧,交于一点,连接这点与B得到BF,即可求解;
(2)由E是AD的中点得到,由矩形的性质得到,根据“ASA”即可求解.
【详解】(1)解:根据角平分线作法画图如下,射线BF为所求作的角平分线,
(2)证明:∵E是AD的中点,
∴AE=DE .
∵四边形ABCD是矩形,
∴∠A=∠ADC=∠ADF=90°,
在△ABE和△DFE中
∴.
【点睛】本题主要考查了全等三角形的判定,作图-基本作图:熟练掌握角平分线的作法是解决问题的关键.
29.(1)见解析
(2)见解析
【分析】(1)按步骤尺规作图即可;
(2)如图:连结、,由(1)作图可得、,然后再运用SSS证明≌,最后运用全等三角形的性质即可证明结论.
【详解】(1)解:如图所示,即为所求的平分线.
(2)解:连结、
由(1)作图可知,
在和中,
,,(公共边)
∴
∴(全等三角形对应角相等).
【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点,掌握尺规作图作角平分线成为解答本题的关键.
30.(1)作图见解析;(2)作图见解析;(3)证明见解析.
【详解】试题分析:(1)①以B为圆心,任意长为半径画弧,交AB、BC于F、N,再以F、N为圆心,大于FN长为半径画弧,两弧交于点M,过B、M画射线,交AC于D,线段BD就是∠B的平分线;
(2)分别以A、B为圆心,大于AB长为半径画弧,两弧交于X、Y,过X、Y画直线与AB交于点E,点E就是AB的中点;
(3)首先根据角平分线的性质可得∠ABD的度数,进而得到∠ABD=∠A,根据等角对等边可得AD=BD,再加上条件AE=BE,ED=ED,即可利用SSS证明△ADE≌△BDE.
试题解析:(1)作出∠B的平分线BD;
(2)作出AB的中点E.
(3)证明:
∵∠ABD=×60°=30°,∠A=30°,
∴∠ABD=∠A,
∴AD=BD,
在△ADE和△BDE中,
∴△ADE≌△BDE(SSS).
