13.2 画轴对称图形 同步练习 (含解析)2022-2023学年上学期广西各地八年级数学期末试题选编
文档属性
| 名称 | 13.2 画轴对称图形 同步练习 (含解析)2022-2023学年上学期广西各地八年级数学期末试题选编 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 16:06:33 | ||
图片预览

文档简介
13.2 画轴对称图形
一、单选题
1.(2022秋·广西贵港·八年级统考期末)若点关于轴对称的点在第一象限,则的取值范围是( )
A. B. C. D.
2.(2022秋·广西贵港·八年级统考期末)已知点A(a,2020)与点B(2022,b)关于x轴对称,则a+b的值为( )
A.﹣1 B.1 C.2 D.3
3.(2022秋·广西贺州·八年级统考期末)如果点和点关于轴对称,则、的值为( )
A., B., C., D.,
4.(2022秋·广西河池·八年级统考期末)如图,是的高,线段与线段关于对称,若,则的度数为( )
A. B. C. D.
二、填空题
5.(2022秋·广西河池·八年级统考期末)已知点,则点A关于x轴的对称点的坐标是 .
6.(2022秋·广西桂林·八年级统考期末)已知点P,关于y轴对称的点的坐标为 .
7.(2022秋·广西贺州·八年级统考期末)在平面直角坐标系中,若点和点是关于轴对称,则 .
8.(2022秋·广西贵港·八年级统考期末)已知点与点关于轴对称,则 .
三、解答题
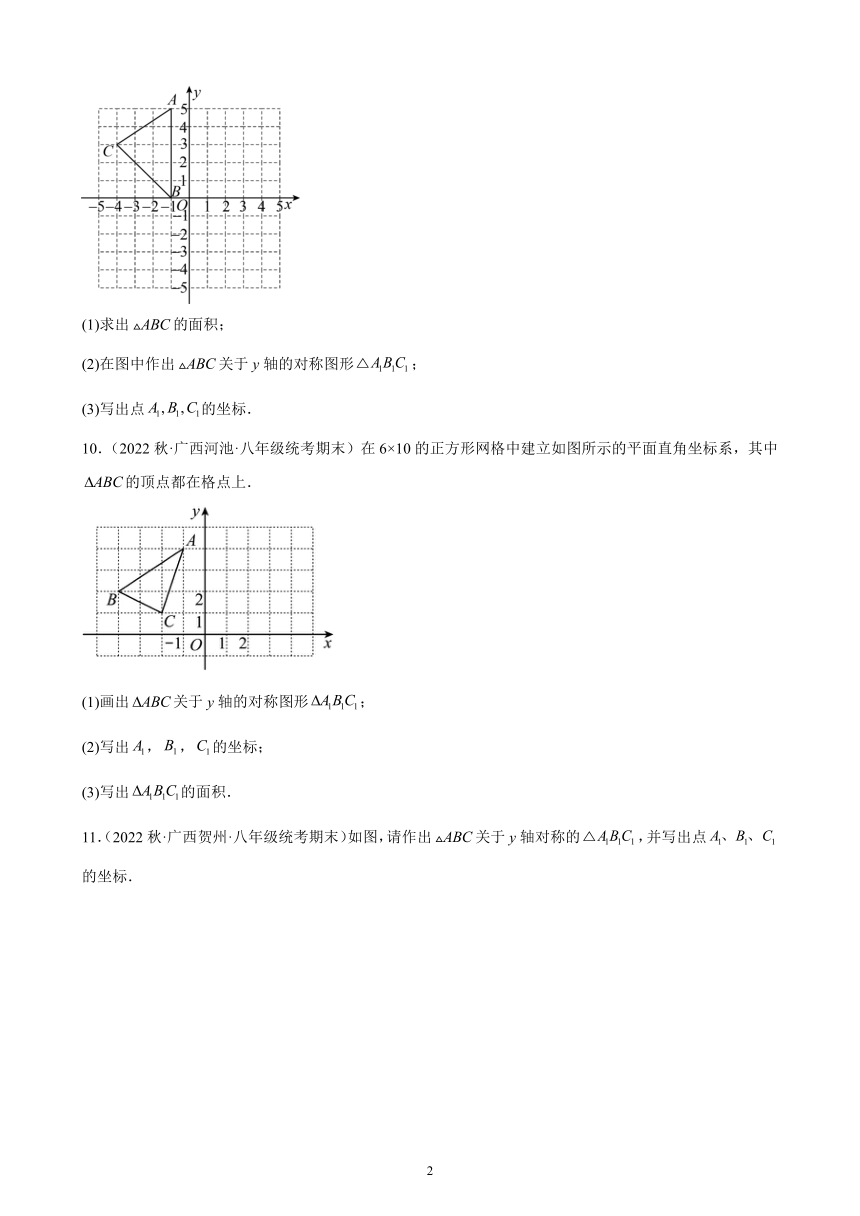
9.(2022秋·广西柳州·八年级统考期末)如图,在平面直角坐标系中,.
(1)求出的面积;
(2)在图中作出关于y轴的对称图形;
(3)写出点的坐标.
10.(2022秋·广西河池·八年级统考期末)在6×10的正方形网格中建立如图所示的平面直角坐标系,其中的顶点都在格点上.
(1)画出关于y轴的对称图形;
(2)写出,,的坐标;
(3)写出的面积.
11.(2022秋·广西贺州·八年级统考期末)如图,请作出关于y轴对称的,并写出点的坐标.
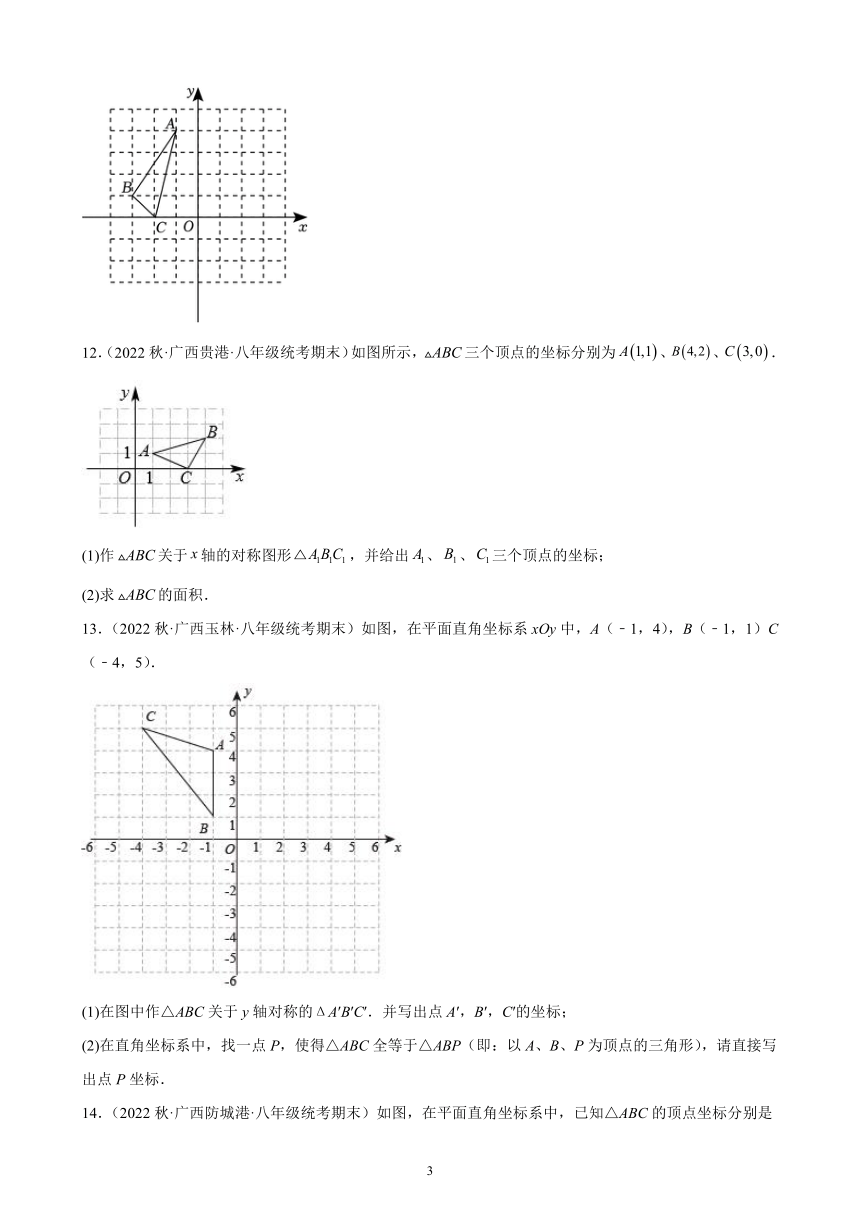
12.(2022秋·广西贵港·八年级统考期末)如图所示,三个顶点的坐标分别为、、.
(1)作关于轴的对称图形,并给出、、三个顶点的坐标;
(2)求的面积.
13.(2022秋·广西玉林·八年级统考期末)如图,在平面直角坐标系xOy中,A(﹣1,4),B(﹣1,1)C(﹣4,5).
(1)在图中作△ABC关于y轴对称的ΔA′B′C′.并写出点A′,B′,C′的坐标;
(2)在直角坐标系中,找一点P,使得△ABC全等于△ABP(即:以A、B、P为顶点的三角形),请直接写出点P坐标.
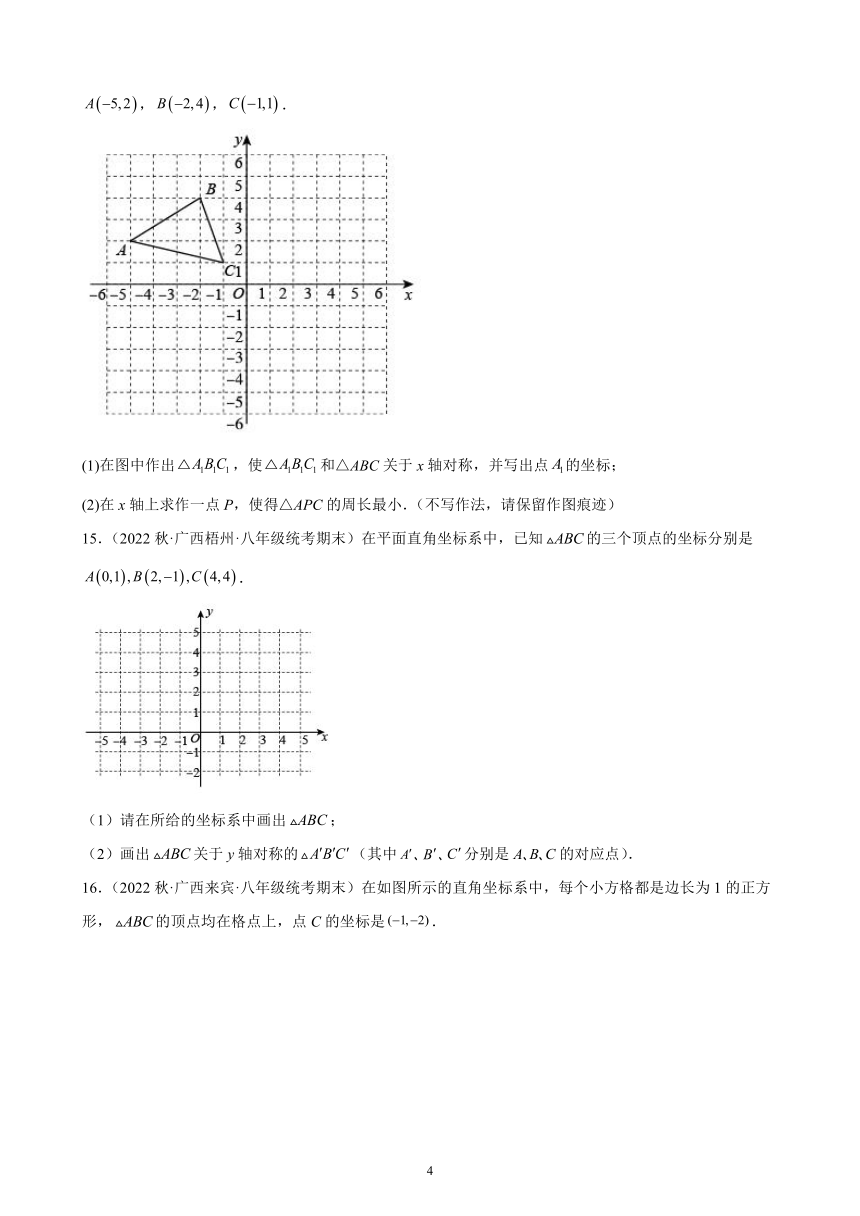
14.(2022秋·广西防城港·八年级统考期末)如图,在平面直角坐标系中,已知△ABC的顶点坐标分别是,,.
(1)在图中作出,使和△ABC关于x轴对称,并写出点的坐标;
(2)在x轴上求作一点P,使得△APC的周长最小.(不写作法,请保留作图痕迹)
15.(2022秋·广西梧州·八年级统考期末)在平面直角坐标系中,已知的三个顶点的坐标分别是.
(1)请在所给的坐标系中画出;
(2)画出关于y轴对称的(其中 分别是A B C的对应点).
16.(2022秋·广西来宾·八年级统考期末)在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,的顶点均在格点上,点C的坐标是.
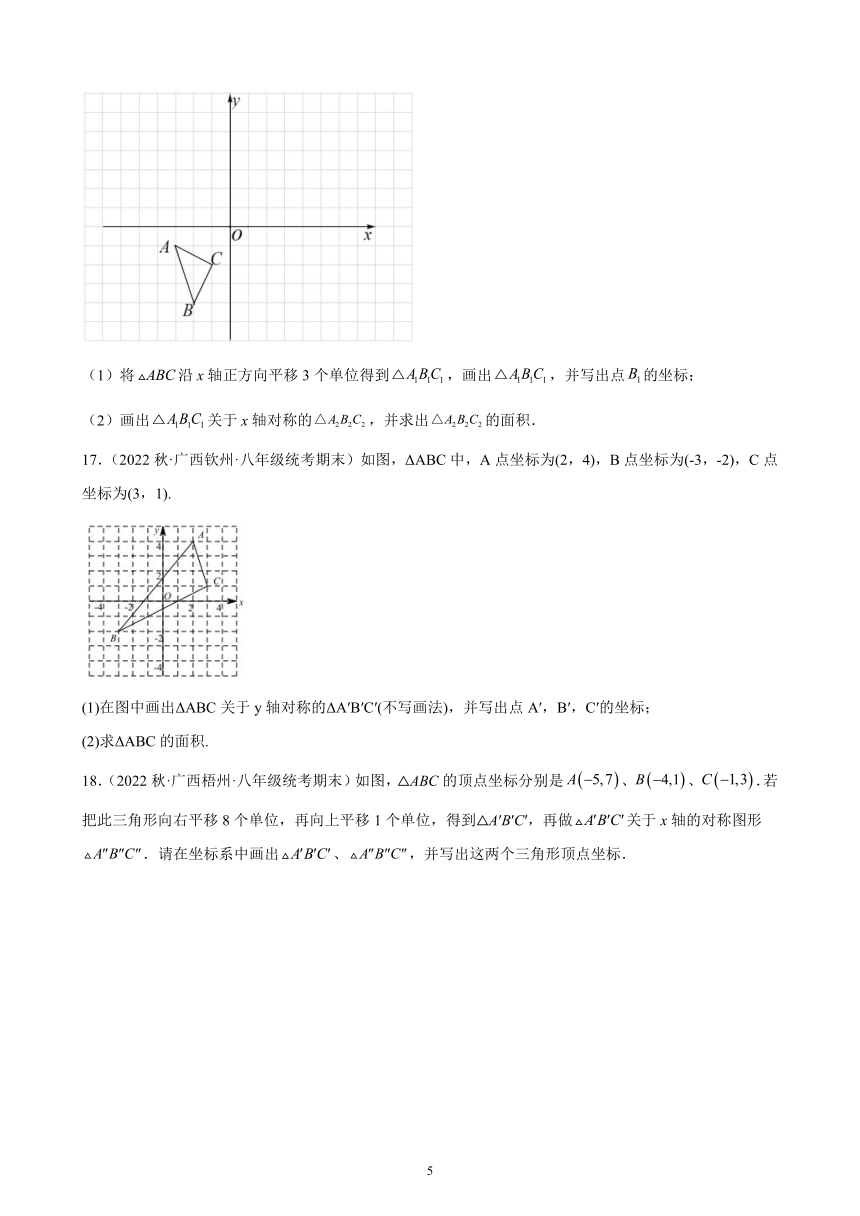
(1)将沿x轴正方向平移3个单位得到,画出,并写出点的坐标;
(2)画出关于x轴对称的,并求出的面积.
17.(2022秋·广西钦州·八年级统考期末)如图,ΔABC中,A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(3,1).
(1)在图中画出ΔABC关于y轴对称的ΔA′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求ΔABC的面积.
18.(2022秋·广西梧州·八年级统考期末)如图,△ABC的顶点坐标分别是、、.若把此三角形向右平移8个单位,再向上平移1个单位,得到△A′B′C′,再做关于x轴的对称图形.请在坐标系中画出、,并写出这两个三角形顶点坐标.
19.(2022秋·广西桂林·八年级统考期末)在边长为1的小正方形网格中,的顶点均在格点上.
(1)点B关于y轴的对称点坐标为___________;点A关于x轴的对称点坐标为___________;
(2)将向左平移3个单位长度得到,请画出;
20.(2022秋·广西贵港·八年级统考期末)在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,的顶点均在格点上,点,点,点
(1)将先向右平移4个单位,再向上平移3个单位得到,画出,并写出点坐标;
(2)画出关于x轴对称的,并写出点的坐标.
21.(2022秋·广西崇左·八年级统考期末)在平面直角坐标系中的位置如图所示.
(1)将向下平移4个单位,商出平移后的.
(2)画出关于y轴对称的,并写出的坐标.
(3)计算的面积.
22.(2022秋·广西河池·八年级统考期末)如图,在平面直角坐标系中,A(4,),B(1,),C(3,).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)直接写出点A1,B1,C1的坐标;
(3)在△A1B1C1中,∠A1=27°,求B1C1边上的高与A1C1所夹角的度数.
23.(2022秋·广西防城港·八年级统考期末)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1向左平移3个单位后得到△A2B2C2,画出△A2B2C2,并写出顶点A2的坐标.
24.(2022秋·广西河池·八年级统考期末)如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)△ABC的面积为 ;
(2)在图中作出△ABC关于直线MN的对称图形△A′B′C′.
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短.( 保留痕迹)
参考答案:
1.B
【分析】先根据关于轴对称的点的坐标特征得到点的对称点的坐标,再利用第一象限内点的坐标特征得到,然后解不等式组即可.
【详解】点关于轴对称的点的坐标为,
而点在第一象限,
,
解得,
即的取值范围为.
故选:.
【点睛】本题考查了关于轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数.也考查了解一元一次不等式组和各个象限内点的坐标的符号特征,熟练掌握知识点是解题的关键.
2.C
【分析】根据关于x轴对称的点的坐标特点即可求出a、b的值;关于x轴对称的点的特点:横坐标相同,纵坐标互为相反数.
【详解】解:点A(a,2020)与点B(2022,b)关于x轴对称,
,
,
故选C.
【点睛】本题考查了关于x轴对称的点坐标的特点,牢记口诀:关于谁对称谁不变,关于原点都改变是解题关键.
3.B
【分析】直接利用关于y轴对称点的性质得出答案.
【详解】解:∵点A(m,2)与点B(3,n)关于y轴对称,
∴m=-3,n=2.
故选:B.
【点睛】本题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
4.A
【分析】根据AD⊥BC和∠B=35°,即可求出∠DAB,根据AB、AE关于AD对称,得到AB=AE,即有∠E=∠B=35°,则根据三角形外角与内角关系有∠ACD=∠E+∠CAE=75°,进而可求出∠CAD,则∠BAC可求.
【详解】解:∵AD是△ABC的高线,
∴AD⊥BC,
∴∠ADB=90°=∠ADC,
∵∠B=35°,
∴∠DAB=90°-∠B=55°,
∵AB、AE关于AD对称,
∴AB=AE,
∴∠E=∠B=35°,
∵∠CAE=40°,
∴∠ACD=∠E+∠CAE=75°,
∴∠CAD=90°-∠ACD=15°,
∴∠BAC=∠DAB+∠CAD=55°+15°=70°,
故选:A.
【点睛】本题考查了对称的性质、三角形高线的性质、三角形的外角与内角的关系以及角的和差关系等知识,根据对称得出∠E=∠B=35°是解答本题的关键.
5.
【分析】根据关于x轴对称的点横坐标相同,纵坐标互为相反数进行求解即可.
【详解】解:点关于x轴的对称点的坐标是,
故答案为:.
【点睛】本题主要考查了坐标与图形变化——轴对称,熟知关于x轴对称的点横坐标相同,纵坐标互为相反数是解题的关键.
6.
【分析】根据点的对称规律:关于y轴对称,纵坐标不变,横坐标互为相反数.
【详解】因为点P,所以点P关于y轴对称的点坐标为∶.
故答案为∶.
【点睛】此题主要考查了平面直角坐标系中对称点的规律.解决本题的关键是掌握好对称点的坐标规律.
7.
【分析】利用关于轴对称点的坐标特点可得答案.
【详解】解:点和点是关于轴对称,
,
解得.
故答案为:.
【点睛】此题主要考查了关于轴对称点的坐标,关键是掌握关于轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变.
8.-8
【分析】直接利用关于y轴对称点的性质“纵坐标相等,横坐标互为相反数”得出a,b的值,再利用有理数的加减运算法则求出答案.
【详解】解:∵点M(a,3)与点N(5,b)关于y轴对称,
∴a=-5,b=3,
则a-b=-5-3=-8.
故答案为:-8.
【点睛】此题主要考查了关于y轴对称点的性质,正确得出a,b的值是解题关键.
9.(1)
(2)见解析
(3)
【分析】(1)利用三角形的面积公式求解即可;
(2)先作出B,C关于y轴的对称点,然后顺次连接即可;
(3)根据点的位置直接写出坐标即可.
【详解】(1)解:由图可得,的面积:;
(2)解:如图所示:
;
(3)解:由图可得:;
【点睛】本题考查了坐标与图形,涉及到轴对称,点的坐标等,掌握相关知识是关键.
10.(1)见解析
(2),,
(3)3.5
【分析】(1)由轴对称的性质作图,即可得出答案;
(2)由所作图形,即可得到点的坐标;
(3)利用间接求面积的方法,即可求出答案.
【详解】(1)解:如图所示:
(2)解:由(1)可知,
,,;
(3)解:的面积;
【点睛】本题考查作图——轴对称变换、坐标与图形,求三角形的面积问题,熟练掌握轴对称的性质是解答本题的关键.
11.图见解析,.
【分析】分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可.
【详解】解:如图所示,即为所求,
.
【点睛】本题主要考查作图—轴对称变换,解题的关键是掌握轴对称变换的定义与性质,并据此得出变换后的对应点.
12.(1)见解析,,,
(2)
【分析】(1)根据轴对称的性质得出、、的位置,然后顺次连接,然后根据所作图形写出坐标即可;
(2)利用割补法求三角形的面积即可.
【详解】(1)解:如图所示:
由图可得:,,;
(2).
【点睛】本题考查作图—轴对称变换、坐标与图形、三角形的面积计算,熟练掌握轴对称的性质是解答本题的关键.
13.(1)A'(1,4),B′(1,1),C'(4,5);
(2)点P的坐标为(﹣4,0)或(2,0)或(2,5)
【分析】(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可得;
(2)根据网格的特点,根据轴对称的性质,以及全等三角形的判定可得.
【详解】(1)解:如图所示,即为所求,
其中A'(1,4),B′(1,1),C'(4,5);
(2)解:如图所示,点P的坐标为(﹣4,0)或(2,0)或(2,5).
【点睛】本题主要考查作图﹣轴对称变换,解题的关键是掌握轴对称变换的定义和性质及全等三角形的判定.
14.(1)见解析,
(2)见解析
【分析】(1)找出各顶点关于x轴的对称点,再顺次连接即可.根据关于x轴对称的点的坐标横坐标不变,纵坐标互为相反数即得出点坐标;
(2)连接,与x轴的交点即为P点.
【详解】(1)如图,为所求,.
(2)如图,点P为所求.
【点睛】本题考查作图—轴对称,轴对称的性质,两点之间线段最短.利用数形结合的思想是解题的关键.
15.(1)见解析;(2)见解析
【分析】(1)先描点A、B、C,在连结线段AB、BC、CA即可;
(2)先作A、B、C关于y轴的对称点A′、B′、C′,再连结线段A′B′、B′C′、C′A′即可.
【详解】解:(1)在平面直角坐标系中描出点A、B、C,连结AB、BC、CA,
如图,就是要画的三角形;
(2)作点A、B、C关于y轴对称的点A′、B′、C′,
连结A′B′、B′C′、C′A′,
如图,就是要画的三角形.
【点睛】本题考查平面直角坐标系中三角形的作法,轴对称图形的作法,掌握平面直角坐标系中三角形的作法,轴对称图形的作法,,关键是先描点,再连结线段是解题关键.
16.(1)作图见解析,;(2)作图见解析,
【分析】(1)先将分别沿x轴正方向平移3个单位得到,再顺次连接即可得到,写出的坐标即可;
(2)将三点分别关于x轴对称至,再顺次连接即可得到,用长方形的面积减去三个直角三角形的面积即可的得到的面积.
【详解】(1)如图所示,即为所求,;
(2)如图所示,即为所求,
.
【点睛】本题考查平移作图以及轴对称作图,理解平移和轴对称的基本性质并掌握画法是解题关键.
17.(1)见解析,A′(-2,4),B′(3,-2),C′(-3,1);(2)
【分析】(1)根据网格结构找出点A′、B′、C′的位置,然后顺次连接即可;(2)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积,然后列式计算即可得解.
【详解】解:(1)如图,
A′(-2,4),B′(3,-2),C′(-3,1);
(2)S△ABC=6×6-×5×6-×6×3-×1×3,
=36-15-9-,
=.
【点睛】本题考查了利用轴对称变换作图,三角形的面积的求解,熟练掌握网格结构准确找出对应点的位置是解题的关键.
18.画图见解析;这两个三角形顶点坐标为、、.、、.
【分析】利用点平移的坐标变换规律写出点,,的坐标,再描点得到,根据关于x轴的对称的点的坐标特征写出点,,的坐标,再描点得到.
【详解】如图,和为所作,、、.、、.
【点睛】本题考查作图—平移、轴对称变换,作轴对称后的图形的依据是轴对称的性质,掌握其基本作图法是解题的关键(先确定图形的关键点,利用轴对称的性质作出关键点的对称点,按照原图形中的方式顺次链接对称点即可).
19.(1),
(2)见解析
【分析】(1)根据平面直角坐标系中点关于坐标轴对称的坐标特点即可得出答案.
(2)根据平移的性质作图即可.
(1)
∵点B(3,2),点A(1,3),
∴点B关于y轴的对称点坐标为(-3,2),点A关于x轴的对称点坐标(1,-3).
故答案为:(-3,2);(1,-3).
(2)
如图,△A1O1B1即为所求.
【点睛】本题考查作图-轴对称变换、平移变换,熟练掌握轴对称和平移的性质是解答本题的关键.
20.(1)图见详解,B1(2,1);
(2)图见详解,B2(2,1);
【分析】(1)利用点平移的坐标特征写出A1、B1、C1的坐标,然后描点即可;
(2)利用关于x轴对称的点的坐标特征写出A2、B2、C2的坐标,然后描点即可.
【详解】(1)解:如图,△A1B1C1为所作,B1(2,1);
(2)解:如图,△A2B2C2为所作,点B2的坐标为(2,1);
【点睛】本题考查了作图-轴对称变换:几何图形都可看作是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了平移变换.
21.(1)作图见解析
(2)作图见解析,B2(3,2)
(3)1.5
【分析】(1)根据直角坐标系和平移的性质作图,即可得到答案
(2)根据直角坐标系和轴对称的性质,得,,,从而完成求解;
(3)根据直角坐标系、正方形和三角形面积的性质计算,即可得到答案.
【详解】(1)∵A(-2,3)、B(-3,2)、C(-1,1)向下平移4个单位得A1(-2,-1)、B1(-3,-2)C1,在平面直角坐标系中描出A1、B1、C1,
如下图;
(2)∵和关于y轴对称,,,
∴,,
如下图;
(3)=2×2-2××2×1-×1×1=1.5.
【点睛】本题考查了直角坐标系、平移、轴对称的知识;解题的关键是熟练掌握直角坐标系、平移、轴对称的性质,从而完成求解.
22.(1)见解析
(2)A1(4,4),B1(1,1),C1(3,1)
(3)18°
【分析】(1)根据A(4,-4),B(1,-1),C(3,-1),即可画出△ABC关于x轴对称的△A1B1C1;
(2)结合(1)即可写出点A1、B1、C1的坐标;
(3)根据△A1B1C1中,∠A1=27°,利用三角形内角和定理即可求B1C1边上的高与A1C1所夹角的度数.
【详解】(1)解:△A1B1C1即为所求;
,
(2)解:根据图象可知:A1(4,4),B1(1,1),C1(3,1);
(3)解:画A1H⊥B1C1,垂足为H,
∵A1H=B1H,
∴∠B1A1H=45°,
∴∠C1A1H=45°-27°=18°.
【点睛】本题考查了作图-轴对称变换,三角形内角和定理,解决本题的关键是掌握轴对称的性质.
23.(1)见解析;
(2)见解析,顶点A2的坐标为(-3,-1)
【分析】(1)根据轴对称的性质得到点A1、B1、C1,顺次连线即可得到△A1B1C1;
(2)根据平移的性质作图并得到点A2的坐标.
【详解】(1)解:如图,△A1B1C1即为所求;
;
(2)解:如图,△A2B2C2即为所求,顶点A2的坐标为(-3,-1).
.
【点睛】此题考查了作图:轴对称作图及平移作图,以及点的坐标,正确掌握轴对称的性质及平移的性质是解题的关键.
24.(1)4;(2)见解析;(3)见解析.
【详解】试题分析:(1)利用矩形的面积减去三个顶点上三角形的面积即可;
(2)分别作出各点关于直线MN的对称点,再顺次连接即可;
(3)连接BC′交直线MN于点P,则点P即为所求点.
试题解析:
(1)S△ABC=3×4- ×2×2-×1×4-×2×3=12-2-3-3=4.
故答案为4;
(2)如图,△A′B′C′即为所求;
(3)如图,点P即为所求.
【点睛】最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合所学轴对称变换来解决,多数情况要作点关于某直线的对称点.
一、单选题
1.(2022秋·广西贵港·八年级统考期末)若点关于轴对称的点在第一象限,则的取值范围是( )
A. B. C. D.
2.(2022秋·广西贵港·八年级统考期末)已知点A(a,2020)与点B(2022,b)关于x轴对称,则a+b的值为( )
A.﹣1 B.1 C.2 D.3
3.(2022秋·广西贺州·八年级统考期末)如果点和点关于轴对称,则、的值为( )
A., B., C., D.,
4.(2022秋·广西河池·八年级统考期末)如图,是的高,线段与线段关于对称,若,则的度数为( )
A. B. C. D.
二、填空题
5.(2022秋·广西河池·八年级统考期末)已知点,则点A关于x轴的对称点的坐标是 .
6.(2022秋·广西桂林·八年级统考期末)已知点P,关于y轴对称的点的坐标为 .
7.(2022秋·广西贺州·八年级统考期末)在平面直角坐标系中,若点和点是关于轴对称,则 .
8.(2022秋·广西贵港·八年级统考期末)已知点与点关于轴对称,则 .
三、解答题
9.(2022秋·广西柳州·八年级统考期末)如图,在平面直角坐标系中,.
(1)求出的面积;
(2)在图中作出关于y轴的对称图形;
(3)写出点的坐标.
10.(2022秋·广西河池·八年级统考期末)在6×10的正方形网格中建立如图所示的平面直角坐标系,其中的顶点都在格点上.
(1)画出关于y轴的对称图形;
(2)写出,,的坐标;
(3)写出的面积.
11.(2022秋·广西贺州·八年级统考期末)如图,请作出关于y轴对称的,并写出点的坐标.
12.(2022秋·广西贵港·八年级统考期末)如图所示,三个顶点的坐标分别为、、.
(1)作关于轴的对称图形,并给出、、三个顶点的坐标;
(2)求的面积.
13.(2022秋·广西玉林·八年级统考期末)如图,在平面直角坐标系xOy中,A(﹣1,4),B(﹣1,1)C(﹣4,5).
(1)在图中作△ABC关于y轴对称的ΔA′B′C′.并写出点A′,B′,C′的坐标;
(2)在直角坐标系中,找一点P,使得△ABC全等于△ABP(即:以A、B、P为顶点的三角形),请直接写出点P坐标.
14.(2022秋·广西防城港·八年级统考期末)如图,在平面直角坐标系中,已知△ABC的顶点坐标分别是,,.
(1)在图中作出,使和△ABC关于x轴对称,并写出点的坐标;
(2)在x轴上求作一点P,使得△APC的周长最小.(不写作法,请保留作图痕迹)
15.(2022秋·广西梧州·八年级统考期末)在平面直角坐标系中,已知的三个顶点的坐标分别是.
(1)请在所给的坐标系中画出;
(2)画出关于y轴对称的(其中 分别是A B C的对应点).
16.(2022秋·广西来宾·八年级统考期末)在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,的顶点均在格点上,点C的坐标是.
(1)将沿x轴正方向平移3个单位得到,画出,并写出点的坐标;
(2)画出关于x轴对称的,并求出的面积.
17.(2022秋·广西钦州·八年级统考期末)如图,ΔABC中,A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(3,1).
(1)在图中画出ΔABC关于y轴对称的ΔA′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求ΔABC的面积.
18.(2022秋·广西梧州·八年级统考期末)如图,△ABC的顶点坐标分别是、、.若把此三角形向右平移8个单位,再向上平移1个单位,得到△A′B′C′,再做关于x轴的对称图形.请在坐标系中画出、,并写出这两个三角形顶点坐标.
19.(2022秋·广西桂林·八年级统考期末)在边长为1的小正方形网格中,的顶点均在格点上.
(1)点B关于y轴的对称点坐标为___________;点A关于x轴的对称点坐标为___________;
(2)将向左平移3个单位长度得到,请画出;
20.(2022秋·广西贵港·八年级统考期末)在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,的顶点均在格点上,点,点,点
(1)将先向右平移4个单位,再向上平移3个单位得到,画出,并写出点坐标;
(2)画出关于x轴对称的,并写出点的坐标.
21.(2022秋·广西崇左·八年级统考期末)在平面直角坐标系中的位置如图所示.
(1)将向下平移4个单位,商出平移后的.
(2)画出关于y轴对称的,并写出的坐标.
(3)计算的面积.
22.(2022秋·广西河池·八年级统考期末)如图,在平面直角坐标系中,A(4,),B(1,),C(3,).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)直接写出点A1,B1,C1的坐标;
(3)在△A1B1C1中,∠A1=27°,求B1C1边上的高与A1C1所夹角的度数.
23.(2022秋·广西防城港·八年级统考期末)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1向左平移3个单位后得到△A2B2C2,画出△A2B2C2,并写出顶点A2的坐标.
24.(2022秋·广西河池·八年级统考期末)如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)△ABC的面积为 ;
(2)在图中作出△ABC关于直线MN的对称图形△A′B′C′.
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短.( 保留痕迹)
参考答案:
1.B
【分析】先根据关于轴对称的点的坐标特征得到点的对称点的坐标,再利用第一象限内点的坐标特征得到,然后解不等式组即可.
【详解】点关于轴对称的点的坐标为,
而点在第一象限,
,
解得,
即的取值范围为.
故选:.
【点睛】本题考查了关于轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数.也考查了解一元一次不等式组和各个象限内点的坐标的符号特征,熟练掌握知识点是解题的关键.
2.C
【分析】根据关于x轴对称的点的坐标特点即可求出a、b的值;关于x轴对称的点的特点:横坐标相同,纵坐标互为相反数.
【详解】解:点A(a,2020)与点B(2022,b)关于x轴对称,
,
,
故选C.
【点睛】本题考查了关于x轴对称的点坐标的特点,牢记口诀:关于谁对称谁不变,关于原点都改变是解题关键.
3.B
【分析】直接利用关于y轴对称点的性质得出答案.
【详解】解:∵点A(m,2)与点B(3,n)关于y轴对称,
∴m=-3,n=2.
故选:B.
【点睛】本题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
4.A
【分析】根据AD⊥BC和∠B=35°,即可求出∠DAB,根据AB、AE关于AD对称,得到AB=AE,即有∠E=∠B=35°,则根据三角形外角与内角关系有∠ACD=∠E+∠CAE=75°,进而可求出∠CAD,则∠BAC可求.
【详解】解:∵AD是△ABC的高线,
∴AD⊥BC,
∴∠ADB=90°=∠ADC,
∵∠B=35°,
∴∠DAB=90°-∠B=55°,
∵AB、AE关于AD对称,
∴AB=AE,
∴∠E=∠B=35°,
∵∠CAE=40°,
∴∠ACD=∠E+∠CAE=75°,
∴∠CAD=90°-∠ACD=15°,
∴∠BAC=∠DAB+∠CAD=55°+15°=70°,
故选:A.
【点睛】本题考查了对称的性质、三角形高线的性质、三角形的外角与内角的关系以及角的和差关系等知识,根据对称得出∠E=∠B=35°是解答本题的关键.
5.
【分析】根据关于x轴对称的点横坐标相同,纵坐标互为相反数进行求解即可.
【详解】解:点关于x轴的对称点的坐标是,
故答案为:.
【点睛】本题主要考查了坐标与图形变化——轴对称,熟知关于x轴对称的点横坐标相同,纵坐标互为相反数是解题的关键.
6.
【分析】根据点的对称规律:关于y轴对称,纵坐标不变,横坐标互为相反数.
【详解】因为点P,所以点P关于y轴对称的点坐标为∶.
故答案为∶.
【点睛】此题主要考查了平面直角坐标系中对称点的规律.解决本题的关键是掌握好对称点的坐标规律.
7.
【分析】利用关于轴对称点的坐标特点可得答案.
【详解】解:点和点是关于轴对称,
,
解得.
故答案为:.
【点睛】此题主要考查了关于轴对称点的坐标,关键是掌握关于轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变.
8.-8
【分析】直接利用关于y轴对称点的性质“纵坐标相等,横坐标互为相反数”得出a,b的值,再利用有理数的加减运算法则求出答案.
【详解】解:∵点M(a,3)与点N(5,b)关于y轴对称,
∴a=-5,b=3,
则a-b=-5-3=-8.
故答案为:-8.
【点睛】此题主要考查了关于y轴对称点的性质,正确得出a,b的值是解题关键.
9.(1)
(2)见解析
(3)
【分析】(1)利用三角形的面积公式求解即可;
(2)先作出B,C关于y轴的对称点,然后顺次连接即可;
(3)根据点的位置直接写出坐标即可.
【详解】(1)解:由图可得,的面积:;
(2)解:如图所示:
;
(3)解:由图可得:;
【点睛】本题考查了坐标与图形,涉及到轴对称,点的坐标等,掌握相关知识是关键.
10.(1)见解析
(2),,
(3)3.5
【分析】(1)由轴对称的性质作图,即可得出答案;
(2)由所作图形,即可得到点的坐标;
(3)利用间接求面积的方法,即可求出答案.
【详解】(1)解:如图所示:
(2)解:由(1)可知,
,,;
(3)解:的面积;
【点睛】本题考查作图——轴对称变换、坐标与图形,求三角形的面积问题,熟练掌握轴对称的性质是解答本题的关键.
11.图见解析,.
【分析】分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可.
【详解】解:如图所示,即为所求,
.
【点睛】本题主要考查作图—轴对称变换,解题的关键是掌握轴对称变换的定义与性质,并据此得出变换后的对应点.
12.(1)见解析,,,
(2)
【分析】(1)根据轴对称的性质得出、、的位置,然后顺次连接,然后根据所作图形写出坐标即可;
(2)利用割补法求三角形的面积即可.
【详解】(1)解:如图所示:
由图可得:,,;
(2).
【点睛】本题考查作图—轴对称变换、坐标与图形、三角形的面积计算,熟练掌握轴对称的性质是解答本题的关键.
13.(1)A'(1,4),B′(1,1),C'(4,5);
(2)点P的坐标为(﹣4,0)或(2,0)或(2,5)
【分析】(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可得;
(2)根据网格的特点,根据轴对称的性质,以及全等三角形的判定可得.
【详解】(1)解:如图所示,即为所求,
其中A'(1,4),B′(1,1),C'(4,5);
(2)解:如图所示,点P的坐标为(﹣4,0)或(2,0)或(2,5).
【点睛】本题主要考查作图﹣轴对称变换,解题的关键是掌握轴对称变换的定义和性质及全等三角形的判定.
14.(1)见解析,
(2)见解析
【分析】(1)找出各顶点关于x轴的对称点,再顺次连接即可.根据关于x轴对称的点的坐标横坐标不变,纵坐标互为相反数即得出点坐标;
(2)连接,与x轴的交点即为P点.
【详解】(1)如图,为所求,.
(2)如图,点P为所求.
【点睛】本题考查作图—轴对称,轴对称的性质,两点之间线段最短.利用数形结合的思想是解题的关键.
15.(1)见解析;(2)见解析
【分析】(1)先描点A、B、C,在连结线段AB、BC、CA即可;
(2)先作A、B、C关于y轴的对称点A′、B′、C′,再连结线段A′B′、B′C′、C′A′即可.
【详解】解:(1)在平面直角坐标系中描出点A、B、C,连结AB、BC、CA,
如图,就是要画的三角形;
(2)作点A、B、C关于y轴对称的点A′、B′、C′,
连结A′B′、B′C′、C′A′,
如图,就是要画的三角形.
【点睛】本题考查平面直角坐标系中三角形的作法,轴对称图形的作法,掌握平面直角坐标系中三角形的作法,轴对称图形的作法,,关键是先描点,再连结线段是解题关键.
16.(1)作图见解析,;(2)作图见解析,
【分析】(1)先将分别沿x轴正方向平移3个单位得到,再顺次连接即可得到,写出的坐标即可;
(2)将三点分别关于x轴对称至,再顺次连接即可得到,用长方形的面积减去三个直角三角形的面积即可的得到的面积.
【详解】(1)如图所示,即为所求,;
(2)如图所示,即为所求,
.
【点睛】本题考查平移作图以及轴对称作图,理解平移和轴对称的基本性质并掌握画法是解题关键.
17.(1)见解析,A′(-2,4),B′(3,-2),C′(-3,1);(2)
【分析】(1)根据网格结构找出点A′、B′、C′的位置,然后顺次连接即可;(2)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积,然后列式计算即可得解.
【详解】解:(1)如图,
A′(-2,4),B′(3,-2),C′(-3,1);
(2)S△ABC=6×6-×5×6-×6×3-×1×3,
=36-15-9-,
=.
【点睛】本题考查了利用轴对称变换作图,三角形的面积的求解,熟练掌握网格结构准确找出对应点的位置是解题的关键.
18.画图见解析;这两个三角形顶点坐标为、、.、、.
【分析】利用点平移的坐标变换规律写出点,,的坐标,再描点得到,根据关于x轴的对称的点的坐标特征写出点,,的坐标,再描点得到.
【详解】如图,和为所作,、、.、、.
【点睛】本题考查作图—平移、轴对称变换,作轴对称后的图形的依据是轴对称的性质,掌握其基本作图法是解题的关键(先确定图形的关键点,利用轴对称的性质作出关键点的对称点,按照原图形中的方式顺次链接对称点即可).
19.(1),
(2)见解析
【分析】(1)根据平面直角坐标系中点关于坐标轴对称的坐标特点即可得出答案.
(2)根据平移的性质作图即可.
(1)
∵点B(3,2),点A(1,3),
∴点B关于y轴的对称点坐标为(-3,2),点A关于x轴的对称点坐标(1,-3).
故答案为:(-3,2);(1,-3).
(2)
如图,△A1O1B1即为所求.
【点睛】本题考查作图-轴对称变换、平移变换,熟练掌握轴对称和平移的性质是解答本题的关键.
20.(1)图见详解,B1(2,1);
(2)图见详解,B2(2,1);
【分析】(1)利用点平移的坐标特征写出A1、B1、C1的坐标,然后描点即可;
(2)利用关于x轴对称的点的坐标特征写出A2、B2、C2的坐标,然后描点即可.
【详解】(1)解:如图,△A1B1C1为所作,B1(2,1);
(2)解:如图,△A2B2C2为所作,点B2的坐标为(2,1);
【点睛】本题考查了作图-轴对称变换:几何图形都可看作是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了平移变换.
21.(1)作图见解析
(2)作图见解析,B2(3,2)
(3)1.5
【分析】(1)根据直角坐标系和平移的性质作图,即可得到答案
(2)根据直角坐标系和轴对称的性质,得,,,从而完成求解;
(3)根据直角坐标系、正方形和三角形面积的性质计算,即可得到答案.
【详解】(1)∵A(-2,3)、B(-3,2)、C(-1,1)向下平移4个单位得A1(-2,-1)、B1(-3,-2)C1,在平面直角坐标系中描出A1、B1、C1,
如下图;
(2)∵和关于y轴对称,,,
∴,,
如下图;
(3)=2×2-2××2×1-×1×1=1.5.
【点睛】本题考查了直角坐标系、平移、轴对称的知识;解题的关键是熟练掌握直角坐标系、平移、轴对称的性质,从而完成求解.
22.(1)见解析
(2)A1(4,4),B1(1,1),C1(3,1)
(3)18°
【分析】(1)根据A(4,-4),B(1,-1),C(3,-1),即可画出△ABC关于x轴对称的△A1B1C1;
(2)结合(1)即可写出点A1、B1、C1的坐标;
(3)根据△A1B1C1中,∠A1=27°,利用三角形内角和定理即可求B1C1边上的高与A1C1所夹角的度数.
【详解】(1)解:△A1B1C1即为所求;
,
(2)解:根据图象可知:A1(4,4),B1(1,1),C1(3,1);
(3)解:画A1H⊥B1C1,垂足为H,
∵A1H=B1H,
∴∠B1A1H=45°,
∴∠C1A1H=45°-27°=18°.
【点睛】本题考查了作图-轴对称变换,三角形内角和定理,解决本题的关键是掌握轴对称的性质.
23.(1)见解析;
(2)见解析,顶点A2的坐标为(-3,-1)
【分析】(1)根据轴对称的性质得到点A1、B1、C1,顺次连线即可得到△A1B1C1;
(2)根据平移的性质作图并得到点A2的坐标.
【详解】(1)解:如图,△A1B1C1即为所求;
;
(2)解:如图,△A2B2C2即为所求,顶点A2的坐标为(-3,-1).
.
【点睛】此题考查了作图:轴对称作图及平移作图,以及点的坐标,正确掌握轴对称的性质及平移的性质是解题的关键.
24.(1)4;(2)见解析;(3)见解析.
【详解】试题分析:(1)利用矩形的面积减去三个顶点上三角形的面积即可;
(2)分别作出各点关于直线MN的对称点,再顺次连接即可;
(3)连接BC′交直线MN于点P,则点P即为所求点.
试题解析:
(1)S△ABC=3×4- ×2×2-×1×4-×2×3=12-2-3-3=4.
故答案为4;
(2)如图,△A′B′C′即为所求;
(3)如图,点P即为所求.
【点睛】最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合所学轴对称变换来解决,多数情况要作点关于某直线的对称点.
