12.3.1 角的平分线的性质 同步讲练(含答案)
文档属性
| 名称 | 12.3.1 角的平分线的性质 同步讲练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 19:03:54 | ||
图片预览




文档简介
12.3角的平分线的性质
第1课时 角的平分线的性质
【知识重点】
知识点1 角的平分线的作法
1. 角的平分线的作法
(1)折叠法:将已知角折叠,使角的两边重合,折痕就是角的平分线所在的直线.
(2)度量法:用量角器度量已知角的度数,并除以2,再用量角器画出这个角的平分线.
(3)尺规作图法:保留作图痕迹,并指出结论.
2. 尺规作图步骤与图示
已知:∠AOB. 求作:∠AOB的平分线.
作法:(1)以点O为圆心,适当长为半径
画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心, 大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC. 射线OC即为所求(如图).
特别解读
1. “大于MN的长为半径画弧”是因为若以小于MN的长为半径,则画出的两弧不能相交;
2.“画射线OC” 不能叙述为“连接OC”,因为角平分线是射线而不是线段.
知识点2 角的平分线的性质
1. 性质定理 角的平分线上的点到角的两边的距离相等.
角的平分线的性质的两个必要条件:
(1)点在角平分线上;
(2)这个点到角两边的距离即点到角两边的垂线段的长度. 两者缺一不可.
2. 几何语言 如图,
∵ OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E,
∴ PD=PE.
特别提醒
●角的平分线的性质是由两个条件(角平分线,垂线) 得到一个结论(线段相等).
●利用角的平分线的性质证明线段相等时,证明的线段是“垂直于角两边的线段”而不是“垂直于角平分线的线段”.
知识点3 证明几何命题的一般步骤
1. 证明一个几何命题的一般步骤
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证的结论的途径,写出证明过程.
2. 推理证明中常见的分析方法
(1)综合法:从已知条件入手,根据已学过的定义、定理、全等的判定方法等,逐步推出要证的结论.
(2)分析法:从要证明的结论出发,根据已学过的定义、定理、全等的判定方法等,寻找使结论成立所需的条件,这样一步步逆推,一直追溯到结论成立的条件与已知条件吻合.
(3)“两头凑”的方法:分别从已知条件和结论入手,当从已知条件推导出的结论与从结论倒推出所需的条件相吻合时,问题可得证.
特别提醒
●证明一个命题的步骤不是固定不变的,要根据题目的情况而定,但是总体必须是完整的,并且证明的过程必须“步步有据”.
●证明几何命题所画图形应符合题意,并具有一般性和代表性. 在画图时,要考虑是否存在不同的情形,若存在,则要分别画出图形, 再分别进行证明.
【经典例题】
【例1】如图,已知:∠AOB,求作:∠AOM=∠AOB.
解题秘方:利用尺规作图作两次角平分线即可.
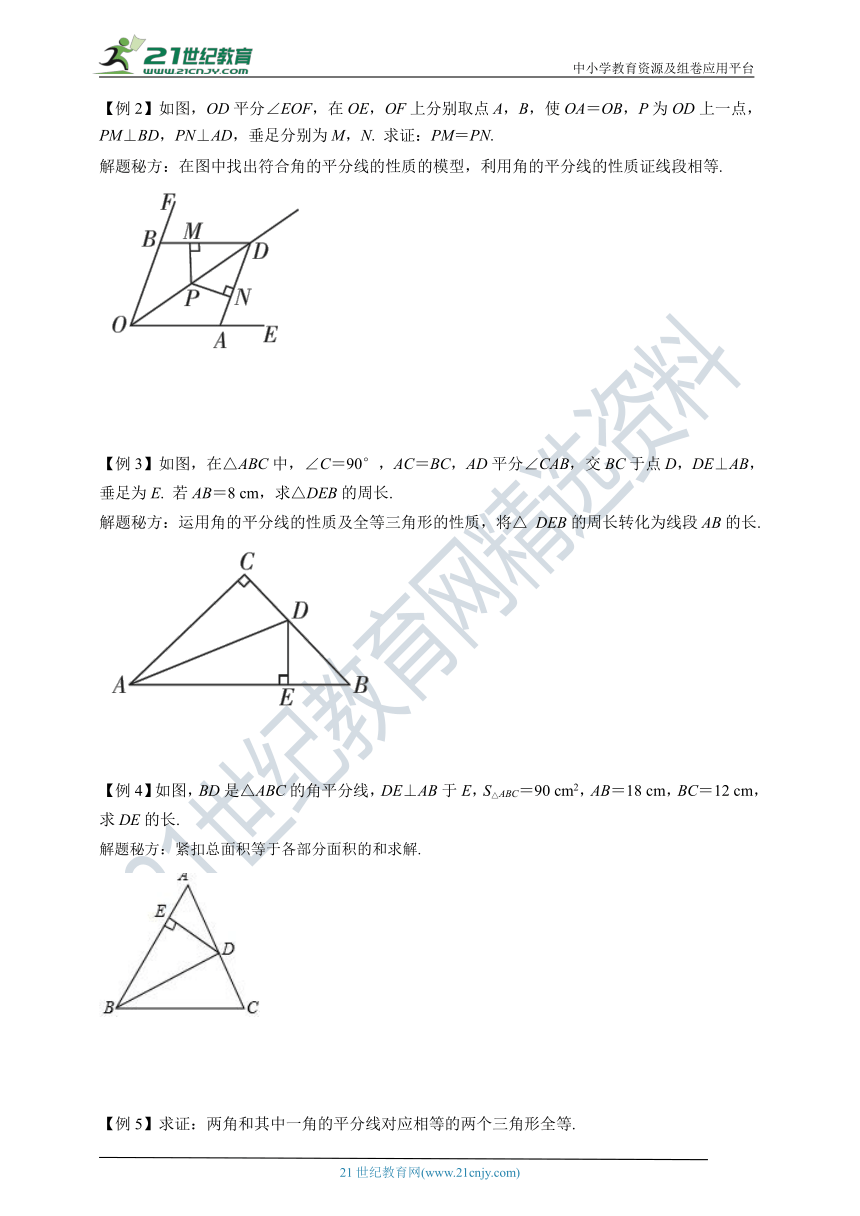
【例2】如图,OD平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P为OD上一点,PM⊥BD,PN⊥AD,垂足分别为M,N. 求证:PM=PN.
解题秘方:在图中找出符合角的平分线的性质的模型,利用角的平分线的性质证线段相等.
【例3】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB,垂足为E. 若AB=8 cm,求△DEB的周长.
解题秘方:运用角的平分线的性质及全等三角形的性质,将△ DEB的周长转化为线段AB的长.
【例4】如图,BD是△ABC的角平分线,DE⊥AB于E,S△ABC=90 cm2,AB=18 cm,BC=12 cm,求DE的长.
解题秘方:紧扣总面积等于各部分面积的和求解.
【例5】求证:两角和其中一角的平分线对应相等的两个三角形全等.
解题秘方:紧扣证明几何命题的一般步骤进行解答.
【同步练习】
一、选择题
1.如图是利用尺规作∠AOB的平分线OC. 在用尺规作角平分线时,用到的三角形全等的判定方法是( )
A. SSS B. SAS C. ASA D. AAS
第1题图 第3题图 第4题图
2.已知∠AOB,求作射线OC,使OC平分∠AOB.①画射线OC即为所求;②以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;③分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C,则上面作法的合理顺序为( )
A.②③① B.③①② C.③②① D.②①③
3.如图,点P是∠AOB的平分线OC上一点,PD⊥OB,垂足为D. 若PD=2,则点P到边OA的距离是( )
A. 1 B. 2 C. D. 4
4.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为( )
A.1 B.2 C.3 D.4
5.如图所示,已知AP,CP分别是△ABC的外角∠DAC,∠ECA的平分线,PM⊥BD,PN⊥BE,垂足分别为M,N,那么PM与PN的大小关系是 ( )
A.PM>PN B.PM=PN C.PM<PN D.无法确定
第5题图 第6题图 第7题图
6.如图,已知在四边形ABCD中, ∠BCD=90 °,BD平分∠ABC,AB=6,BC=9,CD=4, 则四边形ABCD的面积是( )
A. 24 B. 30 C. 36 D. 42
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6 cm,则△DBE的周长是( )
A.6 cm B.7 cm C.8 cm D.9 cm
8.【2021·青海】如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.8 B.7.5 C.15 D.无法确定
9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于 ( )
A.10 B.7 C.5 D.4
第8题图 第9题图 第10题图
10.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB B.PO平分∠APB C.OA=OB D.AB垂直平分OP
11.如图,在△ABC中,∠C=90 °,AD平分∠BAC,DE⊥AB于点E,有下列结论:
① CD=ED;② AC+BE=AB;③∠BDE=∠BAC;④ DA平分∠CDE.
其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
第11题图 第13题图 第14题图
二、填空题
12.“全等三角形对应边上的中线相等”这个命题的已知是________________,结论是___________________.
13.如图,在直角坐标系中,AD是Rt△OAB的角平分线,已知点D的坐标是(0,-3),AB的长是10,则△ABD的面积为 .
14.【2021·长沙】如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=4,DE=1.6,则BD的长为________.
15.如图,AB∥CD,AP,CP分别平分∠BAC,∠ACD,PE⊥AC于点E,且PE=2 cm,则AB与CD之间的距离是___cm.
16.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ABD=∠CBD.若P是BC边上一动点,则DP长的最小值为 .
17.如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,若∠PCB=75°,则∠BAP= .
第15题图 第16题图 第17题图
三、解答题
18.已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M在线段AB的延长线上,点N在线段AC上,且PM=PN.
(1)求证:BM=CN;
(2)写出线段AM,AN与AC之间的数量关系:____________,并说明理由.
19.如图,已知∠MON,点A,C在射线OM上,请按要求完成下列作图(保留画图痕迹)及证明.
(1)在射线ON上分别截取OD=OA,OE=OC,连接AE,DC交于点P,作射线OP;
(2)求证:OP平分∠MON.
20.如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F, 且DB=DC. 求证:BE=CF.
21.求证:三角形一边上的中线小于其他两边和的一半.
22.【感知】如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知DB=DC.
① ② ③
【探究】如图②,AD平分∠BAC,∠B+∠ACD=180°,∠ABD<90°.求证:DB=DC;
【应用】如图③,在四边形ABDC中,∠B=45°,∠C=135°,DB=DC,DE⊥AB,且BE=α,则AB-AC=______(用含α的式子表示).
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,已知:∠AOB,求作:∠AOM=∠AOB.
解题秘方:利用尺规作图作两次角平分线即可.
解:作法:(1)以点O为圆心,适当长为半径画弧,交OA于点E,交OB于点F;(2)分别以点E,F 为圆心,大于EF的长为半径画弧,两弧在∠AOB的内部相交于点C;(3)画射线OC;(4)同理,作∠AOC的平分线OM. ∠AOM 即为所求作的角(如图).
【例2】如图,OD平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P为OD上一点,PM⊥BD,PN⊥AD,垂足分别为M,N. 求证:PM=PN.
解题秘方:在图中找出符合角的平分线的性质的模型,利用角的平分线的性质证线段相等.
证明:∵OD平分∠EOF,∴∠BOD=∠AOD.
在△BOD和△AOD中,
∴△BOD≌△AOD(SAS).
∴∠BDO=∠ADO,即DO平分∠BDA.
又∵ P为DO上一点,且PM⊥BD,PN⊥AD,∴ PM=PN.
【例3】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB,垂足为E. 若AB=8 cm,求△DEB的周长.
解题秘方:运用角的平分线的性质及全等三角形的性质,将△ DEB的周长转化为线段AB的长.
解:在△ABC中,∠C=90°,∴ DC⊥AC.
又∵ DE⊥AB,AD平分∠CAB,∴ DC=DE.
在Rt△ACD和Rt△AED中,
∴ Rt△ACD≌ Rt△AED(HL). ∴ AC=AE.
∵ AC=BC,∴ AE=BC.
∴△DEB的周长=DE+DB+EB=DC+DB+EB=BC+EB=AE+EB=AB=8 cm.
【例4】如图,BD是△ABC的角平分线,DE⊥AB于E,S△ABC=90 cm2,AB=18 cm,BC=12 cm,求DE的长.
解题秘方:紧扣总面积等于各部分面积的和求解.
解:过点D作DF⊥BC,垂足为F,如图12.3-6.
∵ BD是∠ABC的平分线,DE⊥AB,∴ DE=DF.
又∵ S△ABC=S△ABD+S△BDC=×18×DE+×12×DF=90(cm2),
∴ DE=6 cm,即DE的长为6 cm.
【例5】求证:两角和其中一角的平分线对应相等的两个三角形全等.
解题秘方:紧扣证明几何命题的一般步骤进行解答.
解: 已知:如图,在△ABC和△A ′B ′C′中,AD,A′D′分别为∠BAC,∠B′A′C′的平分线,且∠B=∠B′,∠BAC=∠B′A′C′,AD=A′D′. 求证:△ABC≌△A′B′C′.
证明:∵ AD,A′D′分别平分∠BAC,∠B′A′C′,
∴∠1=∠BAC,∠2=∠B′A′C′. ∵∠BAC=∠B′A′C′,
∴∠1=∠2. 在△ABD和△A′B′D′中,
∴△ABD≌△A′B′D′(AAS). ∴ AB=A′B′.
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
【同步练习】
一、选择题
1.如图是利用尺规作∠AOB的平分线OC. 在用尺规作角平分线时,用到的三角形全等的判定方法是( A )
A. SSS B. SAS C. ASA D. AAS
第1题图 第3题图 第4题图
2.已知∠AOB,求作射线OC,使OC平分∠AOB.①画射线OC即为所求;②以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;③分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C,则上面作法的合理顺序为( A )
A.②③① B.③①② C.③②① D.②①③
3.如图,点P是∠AOB的平分线OC上一点,PD⊥OB,垂足为D. 若PD=2,则点P到边OA的距离是( B )
A. 1 B. 2 C. D. 4
4.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为( B )
A.1 B.2 C.3 D.4
5.如图所示,已知AP,CP分别是△ABC的外角∠DAC,∠ECA的平分线,PM⊥BD,PN⊥BE,垂足分别为M,N,那么PM与PN的大小关系是 ( B )
A.PM>PN B.PM=PN C.PM<PN D.无法确定
6.如图,已知在四边形ABCD中, ∠BCD=90 °,BD平分∠ABC,AB=6,BC=9,CD=4, 则四边形ABCD的面积是( B )
A. 24 B. 30 C. 36 D. 42
第5题图 第6题图 第7题图
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6 cm,则△DBE的周长是( A )
A.6 cm B.7 cm C.8 cm D.9 cm
8.【2021·青海】如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( B )
A.8 B.7.5 C.15 D.无法确定
9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于 ( C )
A.10 B.7 C.5 D.4
第8题图 第9题图 第10题图
10.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( D )
A.PA=PB B.PO平分∠APB C.OA=OB D.AB垂直平分OP
11.如图,在△ABC中,∠C=90 °,AD平分∠BAC,DE⊥AB于点E,有下列结论:
① CD=ED;② AC+BE=AB;③∠BDE=∠BAC;④ DA平分∠CDE.
其中正确的结论的个数是( D )
A. 1 B. 2 C. 3 D. 4
第11题图 第13题图 第14题图
二、填空题
12.“全等三角形对应边上的中线相等”这个命题的已知是________________,结论是___________________.
【答案】两个三角形全等 对应边上的中线相等
13.如图,在直角坐标系中,AD是Rt△OAB的角平分线,已知点D的坐标是(0,-3),AB的长是10,则△ABD的面积为 .
【答案】15
14.【2021·长沙】如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=4,DE=1.6,则BD的长为________.
【答案】2.4
15.如图,AB∥CD,AP,CP分别平分∠BAC,∠ACD,PE⊥AC于点E,且PE=2 cm,则AB与CD之间的距离是___cm.
【答案】4
16.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ABD=∠CBD.若P是BC边上一动点,则DP长的最小值为 .
【答案】4
17.如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,若∠PCB=75°,则∠BAP= .
【答案】105°
第15题图 第16题图 第17题图
三、解答题
18.已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M在线段AB的延长线上,点N在线段AC上,且PM=PN.
(1)求证:BM=CN;
证明:∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°.
在Rt△PBM和Rt△PCN中,
∴Rt△PBM≌Rt△PCN(HL).
∴BM=CN.
(2)写出线段AM,AN与AC之间的数量关系:____________,并说明理由.
解:AM+AN=2AC 理由如下:
在Rt△PAB和Rt△PAC中,
∴Rt△PAB≌Rt△PAC(HL).∴AB=AC.
又∵BM=CN,
∴AM+AN=(AB+MB)+(AC-CN)=AB+AC=2AC.
19.如图,已知∠MON,点A,C在射线OM上,请按要求完成下列作图(保留画图痕迹)及证明.
(1)在射线ON上分别截取OD=OA,OE=OC,连接AE,DC交于点P,作射线OP;
(2)求证:OP平分∠MON.
解:(1)如图所示.
(2)证明:在△DOC和△AOE中,
∴△DOC≌△AOE(SAS).∴∠OCD=∠OEA.
∵OD=OA,OE=OC,
∴OE-OD=OC-OA,即DE=AC.
在△APC和△DPE中,
∴△APC≌△DPE(AAS).∴CP=EP.
在△POC和△POE中,
∴△POC≌△POE(SSS).
∴∠COP=∠EOP,即OP平分∠MON.
20.如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F, 且DB=DC. 求证:BE=CF.
证明:∵DE⊥AB,交AB的延长线于点E,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠DFC=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
21.求证:三角形一边上的中线小于其他两边和的一半.
已知:如图,在△ABC中,D是BC边上的中点.
求证:AD<.
证明:如图,延长AD至点E,使得DE=AD,连接BE.
∵D是BC的中点,∴BD=CD.
在△BED和△CAD中,
∴△BED≌△CAD(SAS).
∴BE=AC.
在△ABE中,AE<AB+BE,
∵AE=AD+DE=2AD,∴2AD<AB+BE,
∴2AD<AB+AC,即AD<.
即三角形一边上的中线小于其他两边和的一半.
22.【感知】如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知DB=DC.
① ② ③
【探究】如图②,AD平分∠BAC,∠B+∠ACD=180°,∠ABD<90°.求证:DB=DC;
【应用】如图③,在四边形ABDC中,∠B=45°,∠C=135°,DB=DC,DE⊥AB,且BE=α,则AB-AC=______(用含α的式子表示).
【答案】2α
解:【探究】证明:如图②,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F,则∠F=∠DEB=90°.
∵AD平分∠BAC,∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD. 在△DEB和△DFC中,
∴△DEB≌△DFC(AAS).∴DB=DC.
【应用】提示:如图③,连接AD,过点D作DF⊥AC,交AC的延长线于点F.
第1课时 角的平分线的性质
【知识重点】
知识点1 角的平分线的作法
1. 角的平分线的作法
(1)折叠法:将已知角折叠,使角的两边重合,折痕就是角的平分线所在的直线.
(2)度量法:用量角器度量已知角的度数,并除以2,再用量角器画出这个角的平分线.
(3)尺规作图法:保留作图痕迹,并指出结论.
2. 尺规作图步骤与图示
已知:∠AOB. 求作:∠AOB的平分线.
作法:(1)以点O为圆心,适当长为半径
画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心, 大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC. 射线OC即为所求(如图).
特别解读
1. “大于MN的长为半径画弧”是因为若以小于MN的长为半径,则画出的两弧不能相交;
2.“画射线OC” 不能叙述为“连接OC”,因为角平分线是射线而不是线段.
知识点2 角的平分线的性质
1. 性质定理 角的平分线上的点到角的两边的距离相等.
角的平分线的性质的两个必要条件:
(1)点在角平分线上;
(2)这个点到角两边的距离即点到角两边的垂线段的长度. 两者缺一不可.
2. 几何语言 如图,
∵ OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E,
∴ PD=PE.
特别提醒
●角的平分线的性质是由两个条件(角平分线,垂线) 得到一个结论(线段相等).
●利用角的平分线的性质证明线段相等时,证明的线段是“垂直于角两边的线段”而不是“垂直于角平分线的线段”.
知识点3 证明几何命题的一般步骤
1. 证明一个几何命题的一般步骤
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证的结论的途径,写出证明过程.
2. 推理证明中常见的分析方法
(1)综合法:从已知条件入手,根据已学过的定义、定理、全等的判定方法等,逐步推出要证的结论.
(2)分析法:从要证明的结论出发,根据已学过的定义、定理、全等的判定方法等,寻找使结论成立所需的条件,这样一步步逆推,一直追溯到结论成立的条件与已知条件吻合.
(3)“两头凑”的方法:分别从已知条件和结论入手,当从已知条件推导出的结论与从结论倒推出所需的条件相吻合时,问题可得证.
特别提醒
●证明一个命题的步骤不是固定不变的,要根据题目的情况而定,但是总体必须是完整的,并且证明的过程必须“步步有据”.
●证明几何命题所画图形应符合题意,并具有一般性和代表性. 在画图时,要考虑是否存在不同的情形,若存在,则要分别画出图形, 再分别进行证明.
【经典例题】
【例1】如图,已知:∠AOB,求作:∠AOM=∠AOB.
解题秘方:利用尺规作图作两次角平分线即可.
【例2】如图,OD平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P为OD上一点,PM⊥BD,PN⊥AD,垂足分别为M,N. 求证:PM=PN.
解题秘方:在图中找出符合角的平分线的性质的模型,利用角的平分线的性质证线段相等.
【例3】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB,垂足为E. 若AB=8 cm,求△DEB的周长.
解题秘方:运用角的平分线的性质及全等三角形的性质,将△ DEB的周长转化为线段AB的长.
【例4】如图,BD是△ABC的角平分线,DE⊥AB于E,S△ABC=90 cm2,AB=18 cm,BC=12 cm,求DE的长.
解题秘方:紧扣总面积等于各部分面积的和求解.
【例5】求证:两角和其中一角的平分线对应相等的两个三角形全等.
解题秘方:紧扣证明几何命题的一般步骤进行解答.
【同步练习】
一、选择题
1.如图是利用尺规作∠AOB的平分线OC. 在用尺规作角平分线时,用到的三角形全等的判定方法是( )
A. SSS B. SAS C. ASA D. AAS
第1题图 第3题图 第4题图
2.已知∠AOB,求作射线OC,使OC平分∠AOB.①画射线OC即为所求;②以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;③分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C,则上面作法的合理顺序为( )
A.②③① B.③①② C.③②① D.②①③
3.如图,点P是∠AOB的平分线OC上一点,PD⊥OB,垂足为D. 若PD=2,则点P到边OA的距离是( )
A. 1 B. 2 C. D. 4
4.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为( )
A.1 B.2 C.3 D.4
5.如图所示,已知AP,CP分别是△ABC的外角∠DAC,∠ECA的平分线,PM⊥BD,PN⊥BE,垂足分别为M,N,那么PM与PN的大小关系是 ( )
A.PM>PN B.PM=PN C.PM<PN D.无法确定
第5题图 第6题图 第7题图
6.如图,已知在四边形ABCD中, ∠BCD=90 °,BD平分∠ABC,AB=6,BC=9,CD=4, 则四边形ABCD的面积是( )
A. 24 B. 30 C. 36 D. 42
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6 cm,则△DBE的周长是( )
A.6 cm B.7 cm C.8 cm D.9 cm
8.【2021·青海】如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.8 B.7.5 C.15 D.无法确定
9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于 ( )
A.10 B.7 C.5 D.4
第8题图 第9题图 第10题图
10.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB B.PO平分∠APB C.OA=OB D.AB垂直平分OP
11.如图,在△ABC中,∠C=90 °,AD平分∠BAC,DE⊥AB于点E,有下列结论:
① CD=ED;② AC+BE=AB;③∠BDE=∠BAC;④ DA平分∠CDE.
其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
第11题图 第13题图 第14题图
二、填空题
12.“全等三角形对应边上的中线相等”这个命题的已知是________________,结论是___________________.
13.如图,在直角坐标系中,AD是Rt△OAB的角平分线,已知点D的坐标是(0,-3),AB的长是10,则△ABD的面积为 .
14.【2021·长沙】如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=4,DE=1.6,则BD的长为________.
15.如图,AB∥CD,AP,CP分别平分∠BAC,∠ACD,PE⊥AC于点E,且PE=2 cm,则AB与CD之间的距离是___cm.
16.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ABD=∠CBD.若P是BC边上一动点,则DP长的最小值为 .
17.如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,若∠PCB=75°,则∠BAP= .
第15题图 第16题图 第17题图
三、解答题
18.已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M在线段AB的延长线上,点N在线段AC上,且PM=PN.
(1)求证:BM=CN;
(2)写出线段AM,AN与AC之间的数量关系:____________,并说明理由.
19.如图,已知∠MON,点A,C在射线OM上,请按要求完成下列作图(保留画图痕迹)及证明.
(1)在射线ON上分别截取OD=OA,OE=OC,连接AE,DC交于点P,作射线OP;
(2)求证:OP平分∠MON.
20.如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F, 且DB=DC. 求证:BE=CF.
21.求证:三角形一边上的中线小于其他两边和的一半.
22.【感知】如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知DB=DC.
① ② ③
【探究】如图②,AD平分∠BAC,∠B+∠ACD=180°,∠ABD<90°.求证:DB=DC;
【应用】如图③,在四边形ABDC中,∠B=45°,∠C=135°,DB=DC,DE⊥AB,且BE=α,则AB-AC=______(用含α的式子表示).
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,已知:∠AOB,求作:∠AOM=∠AOB.
解题秘方:利用尺规作图作两次角平分线即可.
解:作法:(1)以点O为圆心,适当长为半径画弧,交OA于点E,交OB于点F;(2)分别以点E,F 为圆心,大于EF的长为半径画弧,两弧在∠AOB的内部相交于点C;(3)画射线OC;(4)同理,作∠AOC的平分线OM. ∠AOM 即为所求作的角(如图).
【例2】如图,OD平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P为OD上一点,PM⊥BD,PN⊥AD,垂足分别为M,N. 求证:PM=PN.
解题秘方:在图中找出符合角的平分线的性质的模型,利用角的平分线的性质证线段相等.
证明:∵OD平分∠EOF,∴∠BOD=∠AOD.
在△BOD和△AOD中,
∴△BOD≌△AOD(SAS).
∴∠BDO=∠ADO,即DO平分∠BDA.
又∵ P为DO上一点,且PM⊥BD,PN⊥AD,∴ PM=PN.
【例3】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB,垂足为E. 若AB=8 cm,求△DEB的周长.
解题秘方:运用角的平分线的性质及全等三角形的性质,将△ DEB的周长转化为线段AB的长.
解:在△ABC中,∠C=90°,∴ DC⊥AC.
又∵ DE⊥AB,AD平分∠CAB,∴ DC=DE.
在Rt△ACD和Rt△AED中,
∴ Rt△ACD≌ Rt△AED(HL). ∴ AC=AE.
∵ AC=BC,∴ AE=BC.
∴△DEB的周长=DE+DB+EB=DC+DB+EB=BC+EB=AE+EB=AB=8 cm.
【例4】如图,BD是△ABC的角平分线,DE⊥AB于E,S△ABC=90 cm2,AB=18 cm,BC=12 cm,求DE的长.
解题秘方:紧扣总面积等于各部分面积的和求解.
解:过点D作DF⊥BC,垂足为F,如图12.3-6.
∵ BD是∠ABC的平分线,DE⊥AB,∴ DE=DF.
又∵ S△ABC=S△ABD+S△BDC=×18×DE+×12×DF=90(cm2),
∴ DE=6 cm,即DE的长为6 cm.
【例5】求证:两角和其中一角的平分线对应相等的两个三角形全等.
解题秘方:紧扣证明几何命题的一般步骤进行解答.
解: 已知:如图,在△ABC和△A ′B ′C′中,AD,A′D′分别为∠BAC,∠B′A′C′的平分线,且∠B=∠B′,∠BAC=∠B′A′C′,AD=A′D′. 求证:△ABC≌△A′B′C′.
证明:∵ AD,A′D′分别平分∠BAC,∠B′A′C′,
∴∠1=∠BAC,∠2=∠B′A′C′. ∵∠BAC=∠B′A′C′,
∴∠1=∠2. 在△ABD和△A′B′D′中,
∴△ABD≌△A′B′D′(AAS). ∴ AB=A′B′.
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
【同步练习】
一、选择题
1.如图是利用尺规作∠AOB的平分线OC. 在用尺规作角平分线时,用到的三角形全等的判定方法是( A )
A. SSS B. SAS C. ASA D. AAS
第1题图 第3题图 第4题图
2.已知∠AOB,求作射线OC,使OC平分∠AOB.①画射线OC即为所求;②以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;③分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C,则上面作法的合理顺序为( A )
A.②③① B.③①② C.③②① D.②①③
3.如图,点P是∠AOB的平分线OC上一点,PD⊥OB,垂足为D. 若PD=2,则点P到边OA的距离是( B )
A. 1 B. 2 C. D. 4
4.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为( B )
A.1 B.2 C.3 D.4
5.如图所示,已知AP,CP分别是△ABC的外角∠DAC,∠ECA的平分线,PM⊥BD,PN⊥BE,垂足分别为M,N,那么PM与PN的大小关系是 ( B )
A.PM>PN B.PM=PN C.PM<PN D.无法确定
6.如图,已知在四边形ABCD中, ∠BCD=90 °,BD平分∠ABC,AB=6,BC=9,CD=4, 则四边形ABCD的面积是( B )
A. 24 B. 30 C. 36 D. 42
第5题图 第6题图 第7题图
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6 cm,则△DBE的周长是( A )
A.6 cm B.7 cm C.8 cm D.9 cm
8.【2021·青海】如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( B )
A.8 B.7.5 C.15 D.无法确定
9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于 ( C )
A.10 B.7 C.5 D.4
第8题图 第9题图 第10题图
10.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( D )
A.PA=PB B.PO平分∠APB C.OA=OB D.AB垂直平分OP
11.如图,在△ABC中,∠C=90 °,AD平分∠BAC,DE⊥AB于点E,有下列结论:
① CD=ED;② AC+BE=AB;③∠BDE=∠BAC;④ DA平分∠CDE.
其中正确的结论的个数是( D )
A. 1 B. 2 C. 3 D. 4
第11题图 第13题图 第14题图
二、填空题
12.“全等三角形对应边上的中线相等”这个命题的已知是________________,结论是___________________.
【答案】两个三角形全等 对应边上的中线相等
13.如图,在直角坐标系中,AD是Rt△OAB的角平分线,已知点D的坐标是(0,-3),AB的长是10,则△ABD的面积为 .
【答案】15
14.【2021·长沙】如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=4,DE=1.6,则BD的长为________.
【答案】2.4
15.如图,AB∥CD,AP,CP分别平分∠BAC,∠ACD,PE⊥AC于点E,且PE=2 cm,则AB与CD之间的距离是___cm.
【答案】4
16.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ABD=∠CBD.若P是BC边上一动点,则DP长的最小值为 .
【答案】4
17.如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,若∠PCB=75°,则∠BAP= .
【答案】105°
第15题图 第16题图 第17题图
三、解答题
18.已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M在线段AB的延长线上,点N在线段AC上,且PM=PN.
(1)求证:BM=CN;
证明:∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°.
在Rt△PBM和Rt△PCN中,
∴Rt△PBM≌Rt△PCN(HL).
∴BM=CN.
(2)写出线段AM,AN与AC之间的数量关系:____________,并说明理由.
解:AM+AN=2AC 理由如下:
在Rt△PAB和Rt△PAC中,
∴Rt△PAB≌Rt△PAC(HL).∴AB=AC.
又∵BM=CN,
∴AM+AN=(AB+MB)+(AC-CN)=AB+AC=2AC.
19.如图,已知∠MON,点A,C在射线OM上,请按要求完成下列作图(保留画图痕迹)及证明.
(1)在射线ON上分别截取OD=OA,OE=OC,连接AE,DC交于点P,作射线OP;
(2)求证:OP平分∠MON.
解:(1)如图所示.
(2)证明:在△DOC和△AOE中,
∴△DOC≌△AOE(SAS).∴∠OCD=∠OEA.
∵OD=OA,OE=OC,
∴OE-OD=OC-OA,即DE=AC.
在△APC和△DPE中,
∴△APC≌△DPE(AAS).∴CP=EP.
在△POC和△POE中,
∴△POC≌△POE(SSS).
∴∠COP=∠EOP,即OP平分∠MON.
20.如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F, 且DB=DC. 求证:BE=CF.
证明:∵DE⊥AB,交AB的延长线于点E,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠DFC=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
21.求证:三角形一边上的中线小于其他两边和的一半.
已知:如图,在△ABC中,D是BC边上的中点.
求证:AD<.
证明:如图,延长AD至点E,使得DE=AD,连接BE.
∵D是BC的中点,∴BD=CD.
在△BED和△CAD中,
∴△BED≌△CAD(SAS).
∴BE=AC.
在△ABE中,AE<AB+BE,
∵AE=AD+DE=2AD,∴2AD<AB+BE,
∴2AD<AB+AC,即AD<.
即三角形一边上的中线小于其他两边和的一半.
22.【感知】如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知DB=DC.
① ② ③
【探究】如图②,AD平分∠BAC,∠B+∠ACD=180°,∠ABD<90°.求证:DB=DC;
【应用】如图③,在四边形ABDC中,∠B=45°,∠C=135°,DB=DC,DE⊥AB,且BE=α,则AB-AC=______(用含α的式子表示).
【答案】2α
解:【探究】证明:如图②,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F,则∠F=∠DEB=90°.
∵AD平分∠BAC,∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD. 在△DEB和△DFC中,
∴△DEB≌△DFC(AAS).∴DB=DC.
【应用】提示:如图③,连接AD,过点D作DF⊥AC,交AC的延长线于点F.
