12.3.2 角的平分线的判定 同步讲练(含答案)
文档属性
| 名称 | 12.3.2 角的平分线的判定 同步讲练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 19:05:18 | ||
图片预览



文档简介
12.3角的平分线的性质
第2课时 角的平分线的判定
【知识重点】
知识点1 角的平分线的判定
1. 判定定理 角的内部到角的两边的距离相等的点在角的平分线上.
特别提醒
1. 使用该判定定理的前提是这个点必须在角的内部.
2. 角的平分线的判定是由两个条件(垂线,线段相等) 得到一个结论( 角平分线).
3. 角的平分线的判定定理是证明两角相等的重要依据, 它比利用三角形全等证两角相等更方便快捷.
2. 几何语言 如图,
∵ 点P为∠AOB内一点,PD⊥OA,
PE⊥OB,垂足分别为D,E,
且PD=PE,
∴点P在∠AOB的平分线OC上.
3. 角的平分线的判定定理与性质定理的关系
(1)如图,都与距离有关,即条件PD⊥OA,PE⊥OB都具备;
(2)点在角的平分线上(角的内部的)
点到角两边的距离相等.
知识点2 三角形的角平分线(拓展点)
1. 性质定理 三角形的三条角平分线交于一点,并且这一点到三条边的距离相等. 这一点叫三角形的内心.
2. 几何语言 如图,在△ABC中,AD,BM,CN 分别是∠BAC,∠ABC,∠ACB的平分线,AD,BM,CN交于一点O,且点O到三边BC,AB, AC的距离(OE,OG,OF的长)相等,即OE=OG=OF.
特别解读
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等. 反之,三角形内部到三边距离相等的点是三角形三条角平分线的交点.
【经典例题】
【例1】如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D. 求证:AD平分∠BAC.
解题秘方:利用角的平分线的判定定理证明角平分线时,紧扣点在角的内部且点到角两边的距离相等进行证明.
【例2】如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D. 求证:AD平分∠BAC.
解题秘方:紧扣“到CA,CN的距离相等的点在∠ACN的平分线上”进行证明.
【例3】如图,在△ABC中,点O是∠ABC,∠ACB的平分线的交点,AB+BC+AC=20. 过O作OD⊥BC 于点D. 且OD=3, 求△ABC的面积.
解题秘方:紧扣三角形内角平分线的性质,关键是内心到三边的距离相等.
【同步练习】
一、选择题
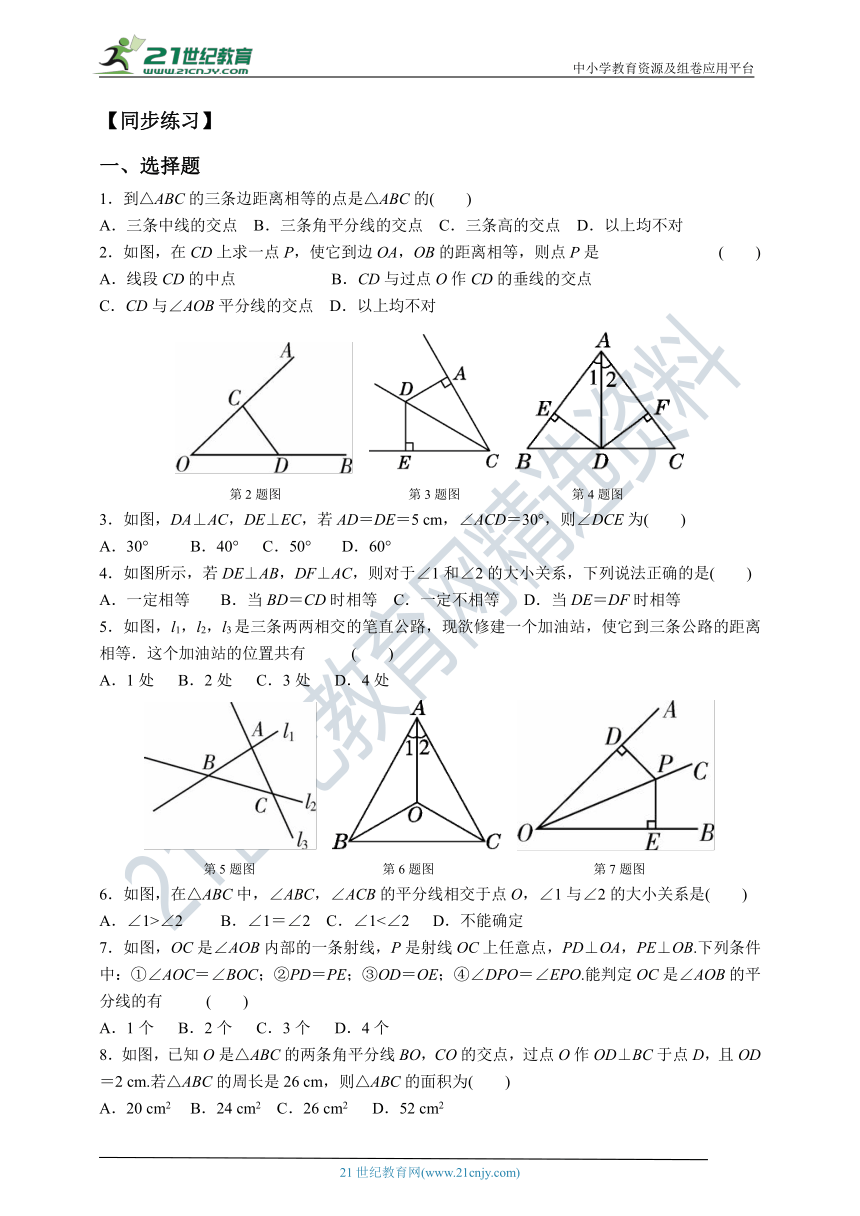
1.到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点 C.三条高的交点 D.以上均不对
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是 ( )
A.线段CD的中点 B.CD与过点O作CD的垂线的交点
C.CD与∠AOB平分线的交点 D.以上均不对
第2题图 第3题图 第4题图
3.如图,DA⊥AC,DE⊥EC,若AD=DE=5 cm,∠ACD=30°,则∠DCE为( )
A.30° B.40° C.50° D.60°
4.如图所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系,下列说法正确的是( )
A.一定相等 B.当BD=CD时相等 C.一定不相等 D.当DE=DF时相等
5.如图,l1,l2,l3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等.这个加油站的位置共有 ( )
A.1处 B.2处 C.3处 D.4处
第5题图 第6题图 第7题图
6.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,∠1与∠2的大小关系是( )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.不能确定
7.如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB.下列条件中:①∠AOC=∠BOC;②PD=PE;③OD=OE;④∠DPO=∠EPO.能判定OC是∠AOB的平分线的有 ( )
A.1个 B.2个 C.3个 D.4个
8.如图,已知O是△ABC的两条角平分线BO,CO的交点,过点O作OD⊥BC于点D,且OD=2 cm.若△ABC的周长是26 cm,则△ABC的面积为( )
A.20 cm2 B.24 cm2 C.26 cm2 D.52 cm2
第8题图 第9题图 第10题图
9.【唐山市第十二中学校考期末】如图,O是△ABC内一点,且O到△ABC三边AB,BC,CA的距离OF=OD=OE,若∠BAC=66°,则∠BOC的度数为( )
A.120° B.130° C.123° D.125°
10.如图,在△ABC中,∠ABC=90°,点I为△ABC各内角平分线的交点,过I点作AC的垂线,垂足为H,若BC=3,AB=4,AC=5,那么IH的值为( )
A.1 B. C.2 D.
11.如图,△ABC的三边AB,BC,CA的长分别是30,40,50,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
第11题图 第14题图 第15题图
二、填空题
12.角的内部到角的两边的________相等的点在角的__________上.因此,判定角平分线,需要满足两个条件:“________”和“_______”;其一般思路是“作垂线,证相等”.
13.三角形的三条角平分线相交于一点,并且这一点到______________相等.
14.如图,点P为△ABC三条角平分线的交点,PD⊥AB,PE⊥BC,PF⊥AC,则PD______PE______PF.
15.如图,PM⊥AC于点M,PN⊥AB于点N,PM=2,当PN=___时,点P在∠BAC的平分线上.
16.如图,点O在一块直角三角尺ABC上(其中∠ABC=30°),OM⊥AB于点M,ON⊥BC于点N,若OM=ON,则∠ABO=______°.
第16题图 第17题图
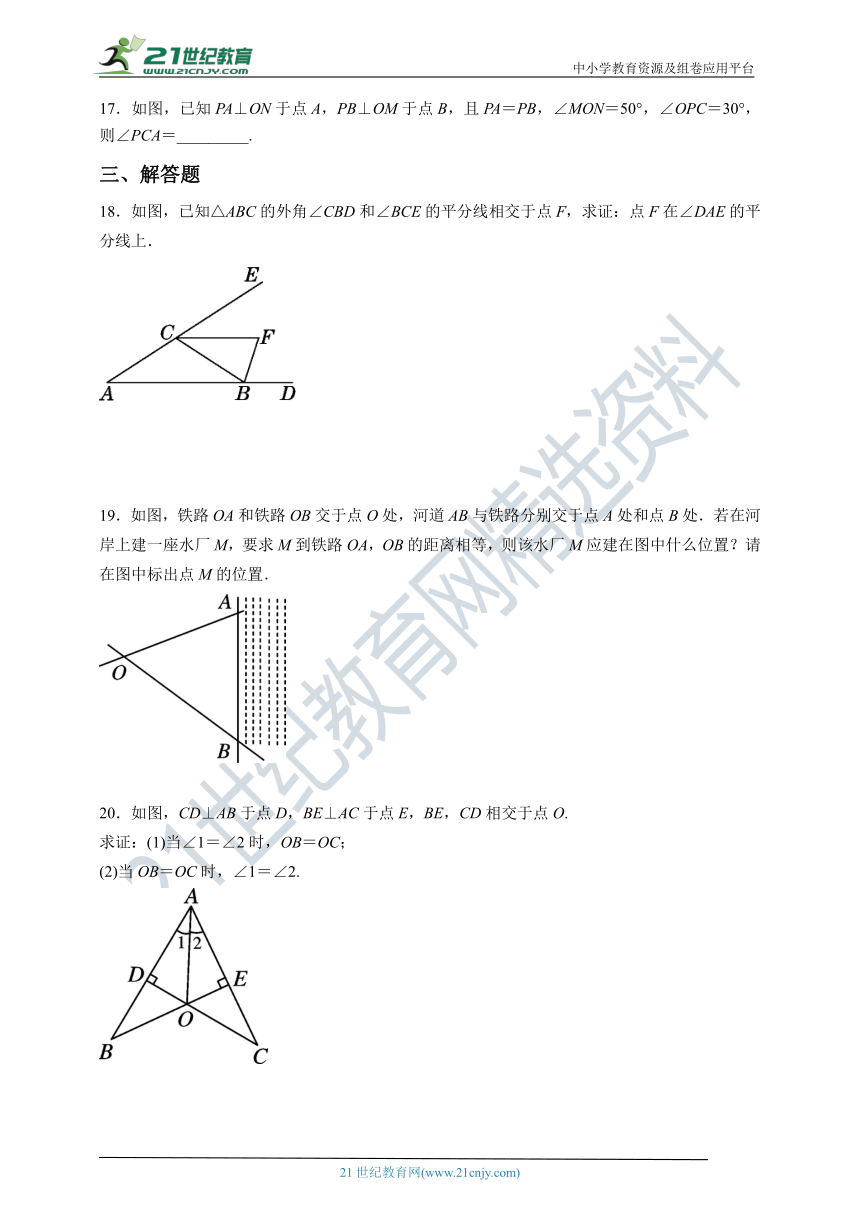
17.如图,已知PA⊥ON于点A,PB⊥OM于点B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=_________.
三、解答题
18.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
19.如图,铁路OA和铁路OB交于点O处,河道AB与铁路分别交于点A处和点B处.若在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出点M的位置.
20.如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点O.
求证:(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
21.【关注社会生活】如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,请用尺规作图找出符合实际要求的点.
22.如图,在四边形ABDC中,∠B=∠D=90°,O为BD的中点,且AO平分∠BAC.求证:
(1)CO平分∠ACD;
(2)OA⊥OC;
(3)AB+CD=AC.
23.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D. 求证:AD平分∠BAC.
解题秘方:利用角的平分线的判定定理证明角平分线时,紧扣点在角的内部且点到角两边的距离相等进行证明.
证明:∵ BF⊥AC,CE⊥AB,∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS). ∴ DE=DF.
又∵ BF⊥AC,CE⊥AB,∴ AD平分∠BAC.
【例2】如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D. 求证:AD平分∠BAC.
解题秘方:紧扣“到CA,CN的距离相等的点在∠ACN的平分线上”进行证明.
证明: 如图, 过点D作DE⊥BM于点E,
DF⊥BN于点F,DG⊥AC于点G.
∵ BD平分∠ABC,∴ DE=DF.
∵ AD平分∠MAC,
∴ DE=DG. ∴ DG=DF,
∴ CD平分∠ACN.
【例3】如图,在△ABC中,点O是∠ABC,∠ACB的平分线的交点,AB+BC+AC=20. 过O作OD⊥BC 于点D. 且OD=3, 求△ABC的面积.
解题秘方:紧扣三角形内角平分线的性质,关键是内心到三边的距离相等.
解: 如图, 过点O作OE⊥AB于点E,
OF⊥AC于点F,连接OA.
∵点O是∠ABC的平分线与∠ACB的平分线
的交点,∴ OE=OD,OF=OD,即OE=OF=OD=3.
∴ S△ABC=S△ABO+S△BCO+S△ACO=AB·OE+BC·OD+ AC·OF=×3×( AB+BC+AC)=×3×20=30.
【同步练习】
一、选择题
1.到△ABC的三条边距离相等的点是△ABC的( B )
A.三条中线的交点 B.三条角平分线的交点 C.三条高的交点 D.以上均不对
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是 ( C )
A.线段CD的中点 B.CD与过点O作CD的垂线的交点
C.CD与∠AOB平分线的交点 D.以上均不对
第2题图 第3题图 第4题图
3.如图,DA⊥AC,DE⊥EC,若AD=DE=5 cm,∠ACD=30°,则∠DCE为( A )
A.30° B.40° C.50° D.60°
4.如图所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系,下列说法正确的是( D )
A.一定相等 B.当BD=CD时相等 C.一定不相等 D.当DE=DF时相等
5.如图,l1,l2,l3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等.这个加油站的位置共有 ( D )
A.1处 B.2处 C.3处 D.4处
第5题图 第6题图 第7题图
6.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,∠1与∠2的大小关系是( B )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.不能确定
7.如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB.下列条件中:①∠AOC=∠BOC;②PD=PE;③OD=OE;④∠DPO=∠EPO.能判定OC是∠AOB的平分线的有 ( D )
A.1个 B.2个 C.3个 D.4个
8.如图,已知O是△ABC的两条角平分线BO,CO的交点,过点O作OD⊥BC于点D,且OD=2 cm.若△ABC的周长是26 cm,则△ABC的面积为( C )
A.20 cm2 B.24 cm2 C.26 cm2 D.52 cm2
第8题图 第9题图 第10题图
9.【唐山市第十二中学校考期末】如图,O是△ABC内一点,且O到△ABC三边AB,BC,CA的距离OF=OD=OE,若∠BAC=66°,则∠BOC的度数为( C )
A.120° B.130° C.123° D.125°
10.如图,在△ABC中,∠ABC=90°,点I为△ABC各内角平分线的交点,过I点作AC的垂线,垂足为H,若BC=3,AB=4,AC=5,那么IH的值为( A )
A.1 B. C.2 D.
11.如图,△ABC的三边AB,BC,CA的长分别是30,40,50,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( D )
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
第11题图 第14题图 第15题图
二、填空题
12.角的内部到角的两边的________相等的点在角的__________上.因此,判定角平分线,需要满足两个条件:“________”和“_______”;其一般思路是“作垂线,证相等”.
【答案】距离 平分线 垂直 相等
13.三角形的三条角平分线相交于一点,并且这一点到______________相等.
【答案】三边的距离
14.如图,点P为△ABC三条角平分线的交点,PD⊥AB,PE⊥BC,PF⊥AC,则PD______PE______PF.
【答案】= =
15.如图,PM⊥AC于点M,PN⊥AB于点N,PM=2,当PN=___时,点P在∠BAC的平分线上.
【答案】2
16.如图,点O在一块直角三角尺ABC上(其中∠ABC=30°),OM⊥AB于点M,ON⊥BC于点N,若OM=ON,则∠ABO=______°.
【答案】15
第16题图 第17题图
17.如图,已知PA⊥ON于点A,PB⊥OM于点B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=_________.
【答案】55°
三、解答题
18.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
证明:如图,过点F分别作AE,BC,AD的垂线FP,FM,FN,P,M,N分别为垂足.
∵CF是∠BCE的平分线,∴FP=FM.
同理FM=FN.∴FP=FN.
又∵FP⊥AE,FN⊥AD,∴点F在∠DAE的平分线上.
19.如图,铁路OA和铁路OB交于点O处,河道AB与铁路分别交于点A处和点B处.若在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出点M的位置.
解:图略.提示:∠AOB的平分线与AB的交点即为点M的位置.
20.如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点O.
求证:(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
证明:(1)∵∠1=∠2,
OD⊥AB,OE⊥AC,
∴OD=OE,∠ODB=∠OEC=90°.
在△BOD和△COE中,
∴△BOD≌△COE(ASA).∴OB=OC.
(2)在△BOD和△COE中,
∴△BOD≌△COE(AAS).∴OD=OE.
又∵OD⊥AB,OE⊥AC,
∴AO平分∠BAC,即∠1=∠2.
21.【关注社会生活】如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,请用尺规作图找出符合实际要求的点.
解:如图,P1为三角形两个内角平分线的交点,P2,P3,P4分别为三角形三个外角平分线的交点,所以P1,P2,P3,P4都可以为货物中转站的位置.
22.如图,在四边形ABDC中,∠B=∠D=90°,O为BD的中点,且AO平分∠BAC.求证:
(1)CO平分∠ACD;
(2)OA⊥OC;
(3)AB+CD=AC.
证明:(1)过点O作OE⊥AC于点E.∵∠B=90°,AO平分∠BAC,
∴OB=OE.
∵O为BD的中点,
∴OB=OD.∴OE=OD.
又∵∠D=90°,∠OEC=90°,∴CO平分∠ACD.
(2)在Rt△ABO和Rt△AEO中,
∴Rt△ABO≌Rt△AEO(HL).
∴∠AOB=∠AOE=∠BOE.
同理,∠COD=∠COE=∠DOE.
∴∠AOC=∠AOE+∠COE=∠BOE+∠DOE=×180°=90°.∴OA⊥OC.
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE.同理可得CD=CE.
∵AC=AE+CE,∴AB+CD=AC.
23.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
解:(1)∵EF⊥AB,∠AEF=50°,
∴∠FAE=90°-50°=40°.
∵∠BAD=100°,∴∠CAD=180°-100°-40°=40°.
(2)证明:过点E作EG⊥AD于点G,EH⊥BC于点H,
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,
∴EF=EG.
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,∴EG=EH.
∵EG⊥AD,EH⊥BC,∴DE平分∠ADC.
(3)∵S△ACD=15,
∴×AD×EG+×CD×EH=15.
即×4×EG+×8×EH=15.
又∵EG=EH=EF,∴EF=EG=EH=.
∴S△ABE=×AB×EF=×7×=.
第2课时 角的平分线的判定
【知识重点】
知识点1 角的平分线的判定
1. 判定定理 角的内部到角的两边的距离相等的点在角的平分线上.
特别提醒
1. 使用该判定定理的前提是这个点必须在角的内部.
2. 角的平分线的判定是由两个条件(垂线,线段相等) 得到一个结论( 角平分线).
3. 角的平分线的判定定理是证明两角相等的重要依据, 它比利用三角形全等证两角相等更方便快捷.
2. 几何语言 如图,
∵ 点P为∠AOB内一点,PD⊥OA,
PE⊥OB,垂足分别为D,E,
且PD=PE,
∴点P在∠AOB的平分线OC上.
3. 角的平分线的判定定理与性质定理的关系
(1)如图,都与距离有关,即条件PD⊥OA,PE⊥OB都具备;
(2)点在角的平分线上(角的内部的)
点到角两边的距离相等.
知识点2 三角形的角平分线(拓展点)
1. 性质定理 三角形的三条角平分线交于一点,并且这一点到三条边的距离相等. 这一点叫三角形的内心.
2. 几何语言 如图,在△ABC中,AD,BM,CN 分别是∠BAC,∠ABC,∠ACB的平分线,AD,BM,CN交于一点O,且点O到三边BC,AB, AC的距离(OE,OG,OF的长)相等,即OE=OG=OF.
特别解读
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等. 反之,三角形内部到三边距离相等的点是三角形三条角平分线的交点.
【经典例题】
【例1】如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D. 求证:AD平分∠BAC.
解题秘方:利用角的平分线的判定定理证明角平分线时,紧扣点在角的内部且点到角两边的距离相等进行证明.
【例2】如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D. 求证:AD平分∠BAC.
解题秘方:紧扣“到CA,CN的距离相等的点在∠ACN的平分线上”进行证明.
【例3】如图,在△ABC中,点O是∠ABC,∠ACB的平分线的交点,AB+BC+AC=20. 过O作OD⊥BC 于点D. 且OD=3, 求△ABC的面积.
解题秘方:紧扣三角形内角平分线的性质,关键是内心到三边的距离相等.
【同步练习】
一、选择题
1.到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点 C.三条高的交点 D.以上均不对
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是 ( )
A.线段CD的中点 B.CD与过点O作CD的垂线的交点
C.CD与∠AOB平分线的交点 D.以上均不对
第2题图 第3题图 第4题图
3.如图,DA⊥AC,DE⊥EC,若AD=DE=5 cm,∠ACD=30°,则∠DCE为( )
A.30° B.40° C.50° D.60°
4.如图所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系,下列说法正确的是( )
A.一定相等 B.当BD=CD时相等 C.一定不相等 D.当DE=DF时相等
5.如图,l1,l2,l3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等.这个加油站的位置共有 ( )
A.1处 B.2处 C.3处 D.4处
第5题图 第6题图 第7题图
6.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,∠1与∠2的大小关系是( )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.不能确定
7.如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB.下列条件中:①∠AOC=∠BOC;②PD=PE;③OD=OE;④∠DPO=∠EPO.能判定OC是∠AOB的平分线的有 ( )
A.1个 B.2个 C.3个 D.4个
8.如图,已知O是△ABC的两条角平分线BO,CO的交点,过点O作OD⊥BC于点D,且OD=2 cm.若△ABC的周长是26 cm,则△ABC的面积为( )
A.20 cm2 B.24 cm2 C.26 cm2 D.52 cm2
第8题图 第9题图 第10题图
9.【唐山市第十二中学校考期末】如图,O是△ABC内一点,且O到△ABC三边AB,BC,CA的距离OF=OD=OE,若∠BAC=66°,则∠BOC的度数为( )
A.120° B.130° C.123° D.125°
10.如图,在△ABC中,∠ABC=90°,点I为△ABC各内角平分线的交点,过I点作AC的垂线,垂足为H,若BC=3,AB=4,AC=5,那么IH的值为( )
A.1 B. C.2 D.
11.如图,△ABC的三边AB,BC,CA的长分别是30,40,50,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
第11题图 第14题图 第15题图
二、填空题
12.角的内部到角的两边的________相等的点在角的__________上.因此,判定角平分线,需要满足两个条件:“________”和“_______”;其一般思路是“作垂线,证相等”.
13.三角形的三条角平分线相交于一点,并且这一点到______________相等.
14.如图,点P为△ABC三条角平分线的交点,PD⊥AB,PE⊥BC,PF⊥AC,则PD______PE______PF.
15.如图,PM⊥AC于点M,PN⊥AB于点N,PM=2,当PN=___时,点P在∠BAC的平分线上.
16.如图,点O在一块直角三角尺ABC上(其中∠ABC=30°),OM⊥AB于点M,ON⊥BC于点N,若OM=ON,则∠ABO=______°.
第16题图 第17题图
17.如图,已知PA⊥ON于点A,PB⊥OM于点B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=_________.
三、解答题
18.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
19.如图,铁路OA和铁路OB交于点O处,河道AB与铁路分别交于点A处和点B处.若在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出点M的位置.
20.如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点O.
求证:(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
21.【关注社会生活】如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,请用尺规作图找出符合实际要求的点.
22.如图,在四边形ABDC中,∠B=∠D=90°,O为BD的中点,且AO平分∠BAC.求证:
(1)CO平分∠ACD;
(2)OA⊥OC;
(3)AB+CD=AC.
23.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D. 求证:AD平分∠BAC.
解题秘方:利用角的平分线的判定定理证明角平分线时,紧扣点在角的内部且点到角两边的距离相等进行证明.
证明:∵ BF⊥AC,CE⊥AB,∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS). ∴ DE=DF.
又∵ BF⊥AC,CE⊥AB,∴ AD平分∠BAC.
【例2】如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D. 求证:AD平分∠BAC.
解题秘方:紧扣“到CA,CN的距离相等的点在∠ACN的平分线上”进行证明.
证明: 如图, 过点D作DE⊥BM于点E,
DF⊥BN于点F,DG⊥AC于点G.
∵ BD平分∠ABC,∴ DE=DF.
∵ AD平分∠MAC,
∴ DE=DG. ∴ DG=DF,
∴ CD平分∠ACN.
【例3】如图,在△ABC中,点O是∠ABC,∠ACB的平分线的交点,AB+BC+AC=20. 过O作OD⊥BC 于点D. 且OD=3, 求△ABC的面积.
解题秘方:紧扣三角形内角平分线的性质,关键是内心到三边的距离相等.
解: 如图, 过点O作OE⊥AB于点E,
OF⊥AC于点F,连接OA.
∵点O是∠ABC的平分线与∠ACB的平分线
的交点,∴ OE=OD,OF=OD,即OE=OF=OD=3.
∴ S△ABC=S△ABO+S△BCO+S△ACO=AB·OE+BC·OD+ AC·OF=×3×( AB+BC+AC)=×3×20=30.
【同步练习】
一、选择题
1.到△ABC的三条边距离相等的点是△ABC的( B )
A.三条中线的交点 B.三条角平分线的交点 C.三条高的交点 D.以上均不对
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是 ( C )
A.线段CD的中点 B.CD与过点O作CD的垂线的交点
C.CD与∠AOB平分线的交点 D.以上均不对
第2题图 第3题图 第4题图
3.如图,DA⊥AC,DE⊥EC,若AD=DE=5 cm,∠ACD=30°,则∠DCE为( A )
A.30° B.40° C.50° D.60°
4.如图所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系,下列说法正确的是( D )
A.一定相等 B.当BD=CD时相等 C.一定不相等 D.当DE=DF时相等
5.如图,l1,l2,l3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等.这个加油站的位置共有 ( D )
A.1处 B.2处 C.3处 D.4处
第5题图 第6题图 第7题图
6.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,∠1与∠2的大小关系是( B )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.不能确定
7.如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB.下列条件中:①∠AOC=∠BOC;②PD=PE;③OD=OE;④∠DPO=∠EPO.能判定OC是∠AOB的平分线的有 ( D )
A.1个 B.2个 C.3个 D.4个
8.如图,已知O是△ABC的两条角平分线BO,CO的交点,过点O作OD⊥BC于点D,且OD=2 cm.若△ABC的周长是26 cm,则△ABC的面积为( C )
A.20 cm2 B.24 cm2 C.26 cm2 D.52 cm2
第8题图 第9题图 第10题图
9.【唐山市第十二中学校考期末】如图,O是△ABC内一点,且O到△ABC三边AB,BC,CA的距离OF=OD=OE,若∠BAC=66°,则∠BOC的度数为( C )
A.120° B.130° C.123° D.125°
10.如图,在△ABC中,∠ABC=90°,点I为△ABC各内角平分线的交点,过I点作AC的垂线,垂足为H,若BC=3,AB=4,AC=5,那么IH的值为( A )
A.1 B. C.2 D.
11.如图,△ABC的三边AB,BC,CA的长分别是30,40,50,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( D )
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
第11题图 第14题图 第15题图
二、填空题
12.角的内部到角的两边的________相等的点在角的__________上.因此,判定角平分线,需要满足两个条件:“________”和“_______”;其一般思路是“作垂线,证相等”.
【答案】距离 平分线 垂直 相等
13.三角形的三条角平分线相交于一点,并且这一点到______________相等.
【答案】三边的距离
14.如图,点P为△ABC三条角平分线的交点,PD⊥AB,PE⊥BC,PF⊥AC,则PD______PE______PF.
【答案】= =
15.如图,PM⊥AC于点M,PN⊥AB于点N,PM=2,当PN=___时,点P在∠BAC的平分线上.
【答案】2
16.如图,点O在一块直角三角尺ABC上(其中∠ABC=30°),OM⊥AB于点M,ON⊥BC于点N,若OM=ON,则∠ABO=______°.
【答案】15
第16题图 第17题图
17.如图,已知PA⊥ON于点A,PB⊥OM于点B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=_________.
【答案】55°
三、解答题
18.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
证明:如图,过点F分别作AE,BC,AD的垂线FP,FM,FN,P,M,N分别为垂足.
∵CF是∠BCE的平分线,∴FP=FM.
同理FM=FN.∴FP=FN.
又∵FP⊥AE,FN⊥AD,∴点F在∠DAE的平分线上.
19.如图,铁路OA和铁路OB交于点O处,河道AB与铁路分别交于点A处和点B处.若在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出点M的位置.
解:图略.提示:∠AOB的平分线与AB的交点即为点M的位置.
20.如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点O.
求证:(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
证明:(1)∵∠1=∠2,
OD⊥AB,OE⊥AC,
∴OD=OE,∠ODB=∠OEC=90°.
在△BOD和△COE中,
∴△BOD≌△COE(ASA).∴OB=OC.
(2)在△BOD和△COE中,
∴△BOD≌△COE(AAS).∴OD=OE.
又∵OD⊥AB,OE⊥AC,
∴AO平分∠BAC,即∠1=∠2.
21.【关注社会生活】如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,请用尺规作图找出符合实际要求的点.
解:如图,P1为三角形两个内角平分线的交点,P2,P3,P4分别为三角形三个外角平分线的交点,所以P1,P2,P3,P4都可以为货物中转站的位置.
22.如图,在四边形ABDC中,∠B=∠D=90°,O为BD的中点,且AO平分∠BAC.求证:
(1)CO平分∠ACD;
(2)OA⊥OC;
(3)AB+CD=AC.
证明:(1)过点O作OE⊥AC于点E.∵∠B=90°,AO平分∠BAC,
∴OB=OE.
∵O为BD的中点,
∴OB=OD.∴OE=OD.
又∵∠D=90°,∠OEC=90°,∴CO平分∠ACD.
(2)在Rt△ABO和Rt△AEO中,
∴Rt△ABO≌Rt△AEO(HL).
∴∠AOB=∠AOE=∠BOE.
同理,∠COD=∠COE=∠DOE.
∴∠AOC=∠AOE+∠COE=∠BOE+∠DOE=×180°=90°.∴OA⊥OC.
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE.同理可得CD=CE.
∵AC=AE+CE,∴AB+CD=AC.
23.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
解:(1)∵EF⊥AB,∠AEF=50°,
∴∠FAE=90°-50°=40°.
∵∠BAD=100°,∴∠CAD=180°-100°-40°=40°.
(2)证明:过点E作EG⊥AD于点G,EH⊥BC于点H,
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,
∴EF=EG.
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,∴EG=EH.
∵EG⊥AD,EH⊥BC,∴DE平分∠ADC.
(3)∵S△ACD=15,
∴×AD×EG+×CD×EH=15.
即×4×EG+×8×EH=15.
又∵EG=EH=EF,∴EF=EG=EH=.
∴S△ABE=×AB×EF=×7×=.
