山东省青岛市2023--2024学年九年级上学期月考质检数学试题(无答案)
文档属性
| 名称 | 山东省青岛市2023--2024学年九年级上学期月考质检数学试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 332.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 00:00:00 | ||
图片预览



文档简介
2023—2024 年山东省青岛市九年级月考质检
数 学 试 题
2023.9
(考试时间:120 分钟 满分:150 分)
说明:
1.本试卷分为第 I 卷和第 II 卷两部分,共 26 题. 第 I 卷为选择题,共 10 小题,40 分;第 II
卷为填空题、作图题、解答题,共 16 题,90 分。
2.所有题目均在答.题.卡.上作答,在试题上作答无效。
第 I 卷(共 40 分)
一、选择题:(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一 项是符合题目要求的)
1.下列四个几何体中,从上面看是三角形的是
A B C D
2.下列图形既是轴对称图形又是中心对称图形的是
A B C D
3.如图的数轴上,点 B 与点 C 关于点 A 对称, A 、 B 两点对应的实数是 3 和 1 ,则点 C 所对应
的实数是
A. 1 B. 2 C. 2 1 D. 2 1
4.下列计算正确的是
A. 5a2 4a2 1 B. a7 a4 a3 C. (a3 )2 a5 D. a2 a3 a6
5.华为麒麟 990 芯片采用了最新的 0.000000007 米的工艺制程,数 0.000000007 用科学记数法表示
A. 7 109 B. 7 108 C. 0.7 109 D. 0.7 108
6.如图,直角三角板的直角顶点放在直线 b 上,且 a / /b , 1 55 ,则 2 的度数为
A. 35 B. 45 C. 55 D. 25
第 6 题 第 7 题
7.如图,线段 AB 与线段 CD 关于点 P 对称,若点 A(3, 3) 、 B(5,1) 、 D(3, 1) ,则点 C 的坐标为
A. (3, 3) B. (1, 3) C. (4, 2) D. (2, 4)
8.以下为真命题的是
A.一组对边相等,另一组对边平行的四边形是平行四边形 B.对角线相等的四边形是矩形
C.对角线互相垂直且相等的四边形是正方形
D.有一条对角线平分一个内角的平行四边形为菱形.
9.如图,在 RtABC 中, BAC 90 且 AB 3 , AC 4 ,点 D 是斜边 BC 上的一个动点,过点 D分别作 DM AB 于点 M , DN AC 于点 N ,连接 MN ,则线段 MN 的最小值为
A. B. C.3 D.4
(
1
)
第 9 题 第 10 题
10.如图,等边三角形 OAD 的顶点 A(2, 0) ,延长 OD 至点 C ,使 CD AD ,以 AD , CD 为邻边作 菱形 ABCD ;延长 CB 交 x 轴于点 A1 ,延长 DC 至点 C1 ,使 CC1 CA1 ,以 A1C , CC1 为邻边作菱形
A1 B1C1C ;以此类推,依次得到菱形 A2 B2C2C1 ,菱形 A3 B3C3C2 菱形 An Bn Cn Cn 1 .则菱形 An Bn Cn Cn 1
的面积为
A. 22 n 1 B. 22 n C. 22 n 1 D. 22 n 2
第 II 卷(共 110分)
二、填空题:(本大题共 6 个小题,每小题 5 分,共 30 分)
11.因式分解: (x y)2 2 y(x y) = .
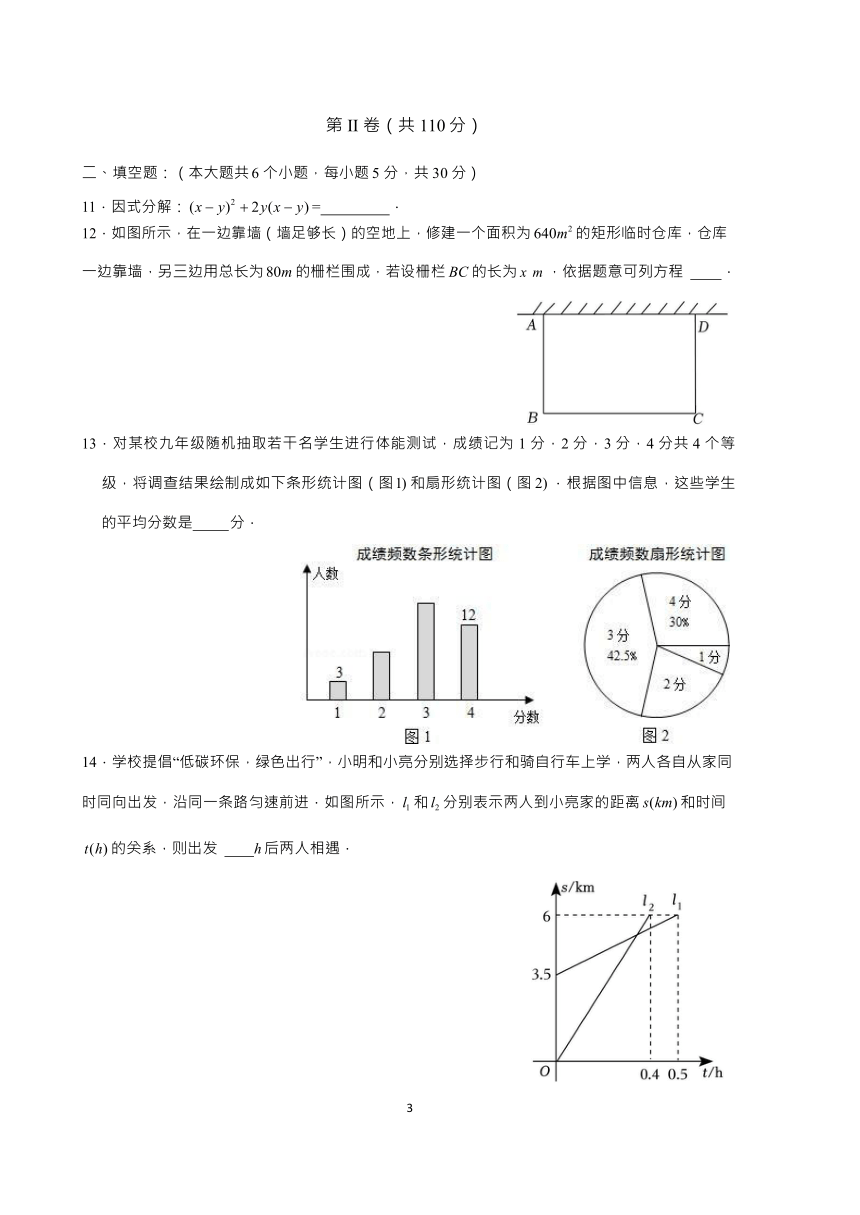
12.如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为 640m2 的矩形临时仓库,仓库 一边靠墙,另三边用总长为 80m 的栅栏围成,若设栅栏 BC 的长为 x m ,依据题意可列方程 .
13.对某校九年级随机抽取若干名学生进行体能测试,成绩记为 1 分,2 分,3 分,4 分共 4 个等 级,将调查结果绘制成如下条形统计图(图 1) 和扇形统计图(图 2) .根据图中信息,这些学生 的平均分数是 分.
14.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同 时同向出发,沿同一条路匀速前进.如图所示, l1 和 l2 分别表示两人到小亮家的距离 s(km) 和时间
t (h) 的关系,则出发 h 后两人相遇.
15.如图,将 ABCD 沿 EF 对折,使点 A 落在点 C 处,若 A 60 , AD 4 , AB 6 ,则 AE 的 长为 .
16.定义:在平面直角坐标系中,对于点 P( x1 , y1 ) ,当点 Q( x2 , y2 ) 满足 2( x1 x2 ) y1 y2 时,称 点 Q( x2 , y2 ) 是点 P( x1 , y1 ) 的“倍增点”.已知点 P1 (1, 0) ,则正确的结论有 .(填 写序号)
①点 Q1 (3, 8) , Q2 (2, 2) 都是点 P1 的“倍增点”;
②若直线 y x 2 上的点 A 是点 P1 的“倍增点”,则点 A 的坐标为 (2, 4) ;
③抛物线 y x2 2x 3 上存在两个点是点 P1 的“倍增点”;
④若点 B 是点 P1 的“倍增点”,则 P1 B 的最小值是;
三、解答题:(本大题共 10 个小题,共 80 分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分 6 分)
已知: ABC , D 为 BA 边上的一点.
求作:点 P ,使 DP / / BC ,且点 P 到 BA , BC 的距离相等.(用直尺、圆规作图,不写作法,但要 保留作图痕迹)
18.(本小题满分 8 分)
解不等式组:,并指出它的所有非负整数解.
19.(本小题满分 8 分)
化简:,再从 1 ,0,1,2 中选一个合适的数代入求值.
20.(本小题满分 10 分)
(1)解一元二次方程: x2 2x 8 0
(2)已知一元二次方程 x2 ax 1 0 的两实数根相等,求 a 的值
21.(本小题满分 10 分) 为了解某校九年级全体男生体能情况,随机抽取了部分男生进行测试,将
测试成绩分为 A 、B 、C 、 D 四个等级,并把成绩绘制成如图所示的两个统计图表,其中“ 7576,78,80,82,82,84,85,85,85,86,86,89.
测试成绩统计表
成绩 x (分 ) 等级 人数
x 90 A 21
75 x 90 B 12
60 x 75 C m
x 60 D n
请根据所给信息,解答下列问题:
(1)填空: m , n ;
(2) B 等级成绩中的众数是 ,中位数是 ;
(3)求扇形统计图中 C 级的圆心角度数;
(4)若该校九年级共有男生 360 人,根据抽样结果,估计体育测试成绩达到 B 级及以上(包 括 B 级)的男生人数.
22.(本小题满分 10 分)
如图,在平面直角坐标系中,点 O 为坐标原点,AB / /OC ,点 B ,C 的坐标分别为 (15, 8) ,(21, 0) , 动点 M 从点 A 沿 A B 以每秒 1 个单位的速度运动;动点 N 从点 C 沿 C O 以每秒 2 个单位的速
度运动. M , N 同时出发,当一个点到达终点后另一个点继续运动,直至到达终点,设运动时间
为 t 秒.
(1)在 t 3 时, M 点坐标 , N 点坐标 .
(2)当 t 为何值时,四边形 OAMN 是矩形?
23.(本小题满分 12 分)
某社区拟建 A ,B 两类摊位以搞活“地摊经济”,每个 A 类摊位的占地面积比每个 B 类摊位的占 地面积多 2 平方米.建 A 类摊位每平方米的费用为 20 元,建 B 类摊位每平方米的费用为 40 元.用
150 平方米建 A 类摊位的个数恰好是用 120 平方米建 B 类摊位个数的 .
(1)求每个 A , B 类摊位占地面积各为多少平方米?
(2)该社区拟建 A ,B 两类摊位共 100 个,且 B 类摊位的数量不少于 A 类摊位数量的 3 倍.建 造多少个 A 类摊位,多少个 B 类摊位,才能使费用最少?并求出建造这 100 个摊位的最少费用.
24.(本小题满分 12 分)
如图,平行四边形 ABCD 的对角线 AC 、 BD 交于点 O , E 为 OC 中点,过点 C 作 CF / / BD 交
BE 的延长线于 F ,连接 DF .
(1)求证: FCE BOE ;
(2)若 AD CD ,当 ADC 满足什么条件时,四边形 OCFD 为正方形?请说明理由.
25.(本小题满分 12 分)
青岛某学校的学生进行综合实践活动时,探究每盆植株培育株数与市场销售价格之间的关系,
通过实验和市场调查发现,每盆植株在 5 株以内(含 5 株),植株的品质较高,单株售价 3 元,超 过 5 株后,每盆每多种 1 株,单株售价降低 0.3 元,当每盆种植株株数超过 12 株后,植株品质较 低,市场统一收购价单株 0.8 元,每盆最多可种植 18 株.
(1)设每盆种植 x(5①则单株售价 元,每盆售价 元(用含 x 的代数式表示);
②当每盆售价为 16.2 元时,求 x 的值.
(2)该学生实验小组共种植了 40 盆,每盆培育所需费用 y (元 ) 与每盆种植株数 x (株 ) 之间 满足 y 2 0.3x ,每盆植株除培育费用外无其他支出.该小组将其中 10 盆赠送给学校,其余放至
市场出售,全部售出后销售所得扣除培育费用后还剩余 100 元,求每盆的种植株数.
26.(本小题满分 12 分)
【模型定义】
如图 1,点 M , N 把线段 AB 分割成 AM , MN 和 BN ,若以 AM , MN , BN 为边的三角形 是一个直角三角形,则称点 M , N 是线段 AB 的勾股分割点.
【探究应用】
①已知点 M , N 是线段 AB 的勾股分割点,若 AM 2 , MN 3 ,则 BN ;
②如图 2,在 ABC 中, FG 是中位线,点 D , E 是线段 BC 的勾股分割点,且 EC DE BD , 连接 AD , AE 分别交 FG 于点 M , N ,求证:点 M , N 是线段 FG 的勾股分割点;
【问题解决】
如图 3,已知点 M ,N 是线段 AB 的勾股分割点,MN AM BN ,四边形 AMDC ,四边形 MNFE
和四边形 NBHG 均是正方形,点 P 在边 EF 上,试探究 SACN , SAPB , SMBH 的数量关系.
数 学 试 题
2023.9
(考试时间:120 分钟 满分:150 分)
说明:
1.本试卷分为第 I 卷和第 II 卷两部分,共 26 题. 第 I 卷为选择题,共 10 小题,40 分;第 II
卷为填空题、作图题、解答题,共 16 题,90 分。
2.所有题目均在答.题.卡.上作答,在试题上作答无效。
第 I 卷(共 40 分)
一、选择题:(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一 项是符合题目要求的)
1.下列四个几何体中,从上面看是三角形的是
A B C D
2.下列图形既是轴对称图形又是中心对称图形的是
A B C D
3.如图的数轴上,点 B 与点 C 关于点 A 对称, A 、 B 两点对应的实数是 3 和 1 ,则点 C 所对应
的实数是
A. 1 B. 2 C. 2 1 D. 2 1
4.下列计算正确的是
A. 5a2 4a2 1 B. a7 a4 a3 C. (a3 )2 a5 D. a2 a3 a6
5.华为麒麟 990 芯片采用了最新的 0.000000007 米的工艺制程,数 0.000000007 用科学记数法表示
A. 7 109 B. 7 108 C. 0.7 109 D. 0.7 108
6.如图,直角三角板的直角顶点放在直线 b 上,且 a / /b , 1 55 ,则 2 的度数为
A. 35 B. 45 C. 55 D. 25
第 6 题 第 7 题
7.如图,线段 AB 与线段 CD 关于点 P 对称,若点 A(3, 3) 、 B(5,1) 、 D(3, 1) ,则点 C 的坐标为
A. (3, 3) B. (1, 3) C. (4, 2) D. (2, 4)
8.以下为真命题的是
A.一组对边相等,另一组对边平行的四边形是平行四边形 B.对角线相等的四边形是矩形
C.对角线互相垂直且相等的四边形是正方形
D.有一条对角线平分一个内角的平行四边形为菱形.
9.如图,在 RtABC 中, BAC 90 且 AB 3 , AC 4 ,点 D 是斜边 BC 上的一个动点,过点 D分别作 DM AB 于点 M , DN AC 于点 N ,连接 MN ,则线段 MN 的最小值为
A. B. C.3 D.4
(
1
)
第 9 题 第 10 题
10.如图,等边三角形 OAD 的顶点 A(2, 0) ,延长 OD 至点 C ,使 CD AD ,以 AD , CD 为邻边作 菱形 ABCD ;延长 CB 交 x 轴于点 A1 ,延长 DC 至点 C1 ,使 CC1 CA1 ,以 A1C , CC1 为邻边作菱形
A1 B1C1C ;以此类推,依次得到菱形 A2 B2C2C1 ,菱形 A3 B3C3C2 菱形 An Bn Cn Cn 1 .则菱形 An Bn Cn Cn 1
的面积为
A. 22 n 1 B. 22 n C. 22 n 1 D. 22 n 2
第 II 卷(共 110分)
二、填空题:(本大题共 6 个小题,每小题 5 分,共 30 分)
11.因式分解: (x y)2 2 y(x y) = .
12.如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为 640m2 的矩形临时仓库,仓库 一边靠墙,另三边用总长为 80m 的栅栏围成,若设栅栏 BC 的长为 x m ,依据题意可列方程 .
13.对某校九年级随机抽取若干名学生进行体能测试,成绩记为 1 分,2 分,3 分,4 分共 4 个等 级,将调查结果绘制成如下条形统计图(图 1) 和扇形统计图(图 2) .根据图中信息,这些学生 的平均分数是 分.
14.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同 时同向出发,沿同一条路匀速前进.如图所示, l1 和 l2 分别表示两人到小亮家的距离 s(km) 和时间
t (h) 的关系,则出发 h 后两人相遇.
15.如图,将 ABCD 沿 EF 对折,使点 A 落在点 C 处,若 A 60 , AD 4 , AB 6 ,则 AE 的 长为 .
16.定义:在平面直角坐标系中,对于点 P( x1 , y1 ) ,当点 Q( x2 , y2 ) 满足 2( x1 x2 ) y1 y2 时,称 点 Q( x2 , y2 ) 是点 P( x1 , y1 ) 的“倍增点”.已知点 P1 (1, 0) ,则正确的结论有 .(填 写序号)
①点 Q1 (3, 8) , Q2 (2, 2) 都是点 P1 的“倍增点”;
②若直线 y x 2 上的点 A 是点 P1 的“倍增点”,则点 A 的坐标为 (2, 4) ;
③抛物线 y x2 2x 3 上存在两个点是点 P1 的“倍增点”;
④若点 B 是点 P1 的“倍增点”,则 P1 B 的最小值是;
三、解答题:(本大题共 10 个小题,共 80 分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分 6 分)
已知: ABC , D 为 BA 边上的一点.
求作:点 P ,使 DP / / BC ,且点 P 到 BA , BC 的距离相等.(用直尺、圆规作图,不写作法,但要 保留作图痕迹)
18.(本小题满分 8 分)
解不等式组:,并指出它的所有非负整数解.
19.(本小题满分 8 分)
化简:,再从 1 ,0,1,2 中选一个合适的数代入求值.
20.(本小题满分 10 分)
(1)解一元二次方程: x2 2x 8 0
(2)已知一元二次方程 x2 ax 1 0 的两实数根相等,求 a 的值
21.(本小题满分 10 分) 为了解某校九年级全体男生体能情况,随机抽取了部分男生进行测试,将
测试成绩分为 A 、B 、C 、 D 四个等级,并把成绩绘制成如图所示的两个统计图表,其中“ 75
测试成绩统计表
成绩 x (分 ) 等级 人数
x 90 A 21
75 x 90 B 12
60 x 75 C m
x 60 D n
请根据所给信息,解答下列问题:
(1)填空: m , n ;
(2) B 等级成绩中的众数是 ,中位数是 ;
(3)求扇形统计图中 C 级的圆心角度数;
(4)若该校九年级共有男生 360 人,根据抽样结果,估计体育测试成绩达到 B 级及以上(包 括 B 级)的男生人数.
22.(本小题满分 10 分)
如图,在平面直角坐标系中,点 O 为坐标原点,AB / /OC ,点 B ,C 的坐标分别为 (15, 8) ,(21, 0) , 动点 M 从点 A 沿 A B 以每秒 1 个单位的速度运动;动点 N 从点 C 沿 C O 以每秒 2 个单位的速
度运动. M , N 同时出发,当一个点到达终点后另一个点继续运动,直至到达终点,设运动时间
为 t 秒.
(1)在 t 3 时, M 点坐标 , N 点坐标 .
(2)当 t 为何值时,四边形 OAMN 是矩形?
23.(本小题满分 12 分)
某社区拟建 A ,B 两类摊位以搞活“地摊经济”,每个 A 类摊位的占地面积比每个 B 类摊位的占 地面积多 2 平方米.建 A 类摊位每平方米的费用为 20 元,建 B 类摊位每平方米的费用为 40 元.用
150 平方米建 A 类摊位的个数恰好是用 120 平方米建 B 类摊位个数的 .
(1)求每个 A , B 类摊位占地面积各为多少平方米?
(2)该社区拟建 A ,B 两类摊位共 100 个,且 B 类摊位的数量不少于 A 类摊位数量的 3 倍.建 造多少个 A 类摊位,多少个 B 类摊位,才能使费用最少?并求出建造这 100 个摊位的最少费用.
24.(本小题满分 12 分)
如图,平行四边形 ABCD 的对角线 AC 、 BD 交于点 O , E 为 OC 中点,过点 C 作 CF / / BD 交
BE 的延长线于 F ,连接 DF .
(1)求证: FCE BOE ;
(2)若 AD CD ,当 ADC 满足什么条件时,四边形 OCFD 为正方形?请说明理由.
25.(本小题满分 12 分)
青岛某学校的学生进行综合实践活动时,探究每盆植株培育株数与市场销售价格之间的关系,
通过实验和市场调查发现,每盆植株在 5 株以内(含 5 株),植株的品质较高,单株售价 3 元,超 过 5 株后,每盆每多种 1 株,单株售价降低 0.3 元,当每盆种植株株数超过 12 株后,植株品质较 低,市场统一收购价单株 0.8 元,每盆最多可种植 18 株.
(1)设每盆种植 x(5
②当每盆售价为 16.2 元时,求 x 的值.
(2)该学生实验小组共种植了 40 盆,每盆培育所需费用 y (元 ) 与每盆种植株数 x (株 ) 之间 满足 y 2 0.3x ,每盆植株除培育费用外无其他支出.该小组将其中 10 盆赠送给学校,其余放至
市场出售,全部售出后销售所得扣除培育费用后还剩余 100 元,求每盆的种植株数.
26.(本小题满分 12 分)
【模型定义】
如图 1,点 M , N 把线段 AB 分割成 AM , MN 和 BN ,若以 AM , MN , BN 为边的三角形 是一个直角三角形,则称点 M , N 是线段 AB 的勾股分割点.
【探究应用】
①已知点 M , N 是线段 AB 的勾股分割点,若 AM 2 , MN 3 ,则 BN ;
②如图 2,在 ABC 中, FG 是中位线,点 D , E 是线段 BC 的勾股分割点,且 EC DE BD , 连接 AD , AE 分别交 FG 于点 M , N ,求证:点 M , N 是线段 FG 的勾股分割点;
【问题解决】
如图 3,已知点 M ,N 是线段 AB 的勾股分割点,MN AM BN ,四边形 AMDC ,四边形 MNFE
和四边形 NBHG 均是正方形,点 P 在边 EF 上,试探究 SACN , SAPB , SMBH 的数量关系.
同课章节目录
