浙江温州瑞安东部及龙湾南部六校联考2023-2024学年九年级上学期开学数学试题(含答案)
文档属性
| 名称 | 浙江温州瑞安东部及龙湾南部六校联考2023-2024学年九年级上学期开学数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 20:07:12 | ||
图片预览


文档简介
2023学年第一学期九年级入学监测数学卷
2023.9
卷首语:
1.本卷共4页,考试时间120分钟,满分120分;
2.全卷由试题卷和答题卡两部分组成,请将答案写在答题卡相应的位置;
3.书写时字迹要工整,清晰,请勿使用涂改液、修正带等,不得使用计算器。
希望你沉着冷静,让智慧在笔尖流淌,用细心为成功奠基!
卷Ⅰ
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选均不给分)
1.若二次根式有意义,则m的取值范围是( )
A. B. C. D.
2.在平面直角坐标系中,若点A(m,2)与点B(3,n)关于y轴对称,则m,n的值分别为( )
A.-3,-2 B.-3,2 C.3,-2 D.3,2
3.下列选项中,化简正确的是( )
A. B. C. D.
4.对温州某社区居民最爱吃的鱼类进行问卷调查后(每人选一种),绘制成如图所示统计图,已知选择带鱼的有45人,那么选择鲳鱼的有( )
(第4题)
A.15人 B.30人 C.45人 D.60人
5.在中,,则的度数是( )
A.70° B.80° C.90° D.110°
6.不等式组的解在数轴上的表示如图所示,则a的值为( )
(第6题)
A.8 B.9 C.10 D.11
7.用因式分解法解方程9x2=(x-2)2时,因式分解结果正确的是( )
A.4(2x-1)(x-1)=0 B.4(2x+1)(x-1)=0
C.4(2x-1)(x+1)=0 D.4(2x+1)(x+1)=0
8.某品牌衬衫原来每件售价400元,经过连续两次降价后,现在每件的售价为200元.设平均每次降价的百分率为x,根据题意所列方程为( )
A.200(1+2x)=400 B.400(1-2x)=200
C.200(1+x)2=400 D.400(1-x)2=200
9.对于反比例函数,当-1<y≤2,且y≠0时,自变量x的取值范围是( )
A.x≥1或x<-2 B.x≥1或x≤-2
C.0<x≤1或x<-2 D.-2<x<0或x≥1
10.在菱形ABCD中,∠B=60°,用六条线段(虚线表示)把菱形分割成四部分,如图所示,其中PM∥EF∥BC,PF∥MN∥CD,FG∥MH∥AC,且点P在对角线AC上,若求该六条割线长(虚线部分)的和,只需知道( )
(第10题)
A.六边形PMHCGF的周长 B.梯形EFGB的周长
C.梯形MNDH的周长 D.菱形ABCD的周长
二、填空题(本题有6小题,每小题4分,共24分)
11.“a的2倍与b的3倍的差”用代数式表示为_________.
12.关于x的方程x2+4x+m=0有两个相等的实数根,则m的值是_________.
13.计算:_________.
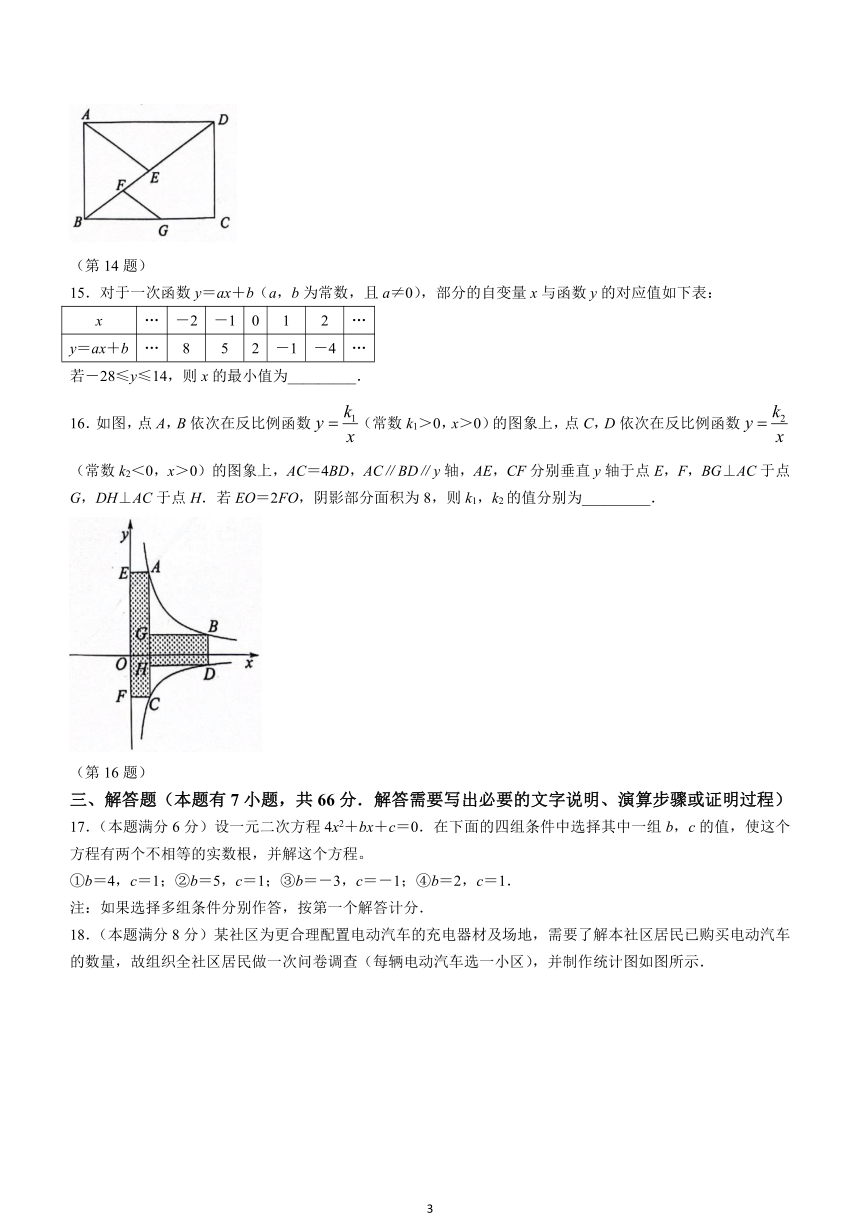
14.如图,在矩形ABCD中,点E,F均在对角线BD上,AE=ED,FG∥AE交边BC于点G.若∠AED=110°,则∠FGC的度数为_________.
(第14题)
15.对于一次函数y=ax+b(a,b为常数,且a≠0),部分的自变量x与函数y的对应值如下表:
x … -2 -1 0 1 2 …
y=ax+b … 8 5 2 -1 -4 …
若-28≤y≤14,则x的最小值为_________.
16.如图,点A,B依次在反比例函数(常数k1>0,x>0)的图象上,点C,D依次在反比例函数(常数k2<0,x>0)的图象上,AC=4BD,AC∥BD∥y轴,AE,CF分别垂直y轴于点E,F,BG⊥AC于点G,DH⊥AC于点H.若EO=2FO,阴影部分面积为8,则k1,k2的值分别为_________.
(第16题)
三、解答题(本题有7小题,共66分.解答需要写出必要的文字说明、演算步骤或证明过程)
17.(本题满分6分)设一元二次方程4x2+bx+c=0.在下面的四组条件中选择其中一组b,c的值,使这个方程有两个不相等的实数根,并解这个方程。
①b=4,c=1;②b=5,c=1;③b=-3,c=-1;④b=2,c=1.
注:如果选择多组条件分别作答,按第一个解答计分.
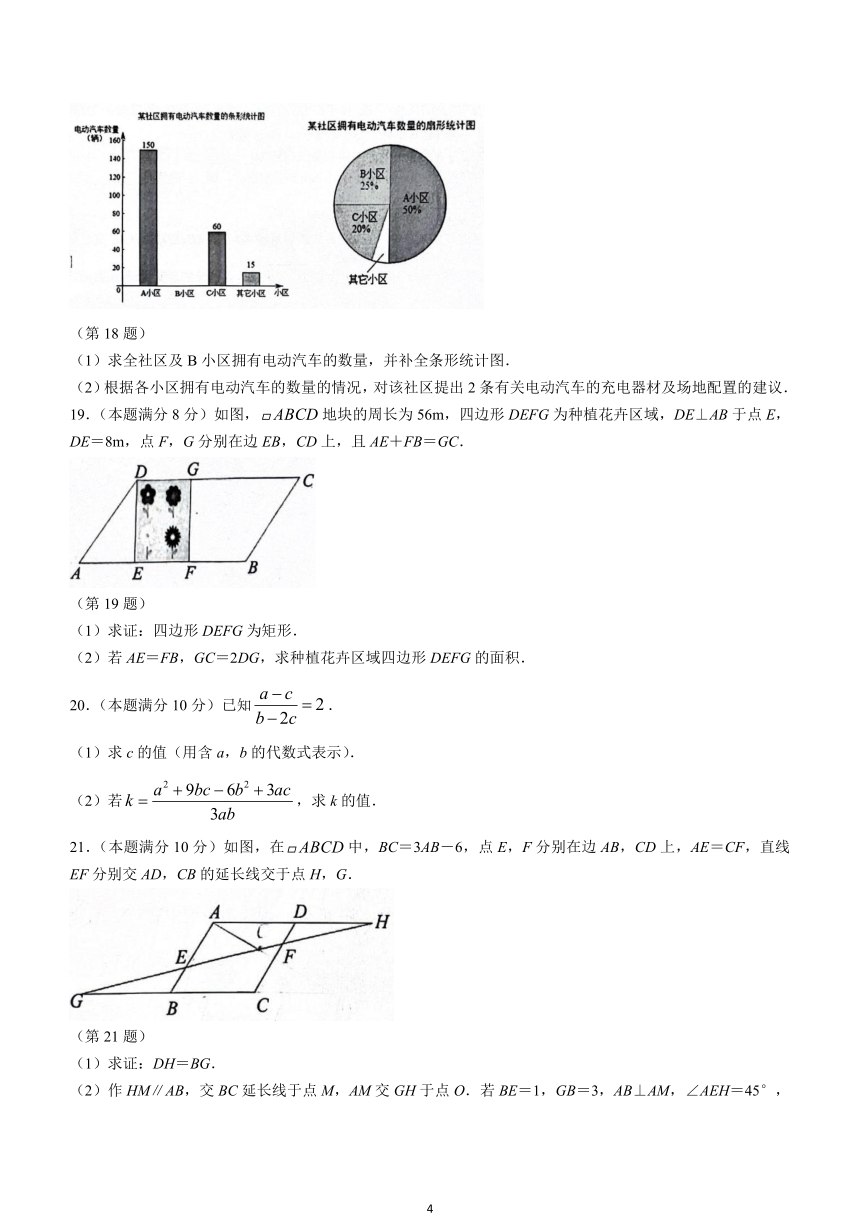
18.(本题满分8分)某社区为更合理配置电动汽车的充电器材及场地,需要了解本社区居民已购买电动汽车的数量,故组织全社区居民做一次问卷调查(每辆电动汽车选一小区),并制作统计图如图所示.
(第18题)
(1)求全社区及B小区拥有电动汽车的数量,并补全条形统计图.
(2)根据各小区拥有电动汽车的数量的情况,对该社区提出2条有关电动汽车的充电器材及场地配置的建议.
19.(本题满分8分)如图,地块的周长为56m,四边形DEFG为种植花卉区域,DE⊥AB于点E,DE=8m,点F,G分别在边EB,CD上,且AE+FB=GC.
(第19题)
(1)求证:四边形DEFG为矩形.
(2)若AE=FB,GC=2DG,求种植花卉区域四边形DEFG的面积.
20.(本题满分10分)已知.
(1)求c的值(用含a,b的代数式表示).
(2)若,求k的值.
21.(本题满分10分)如图,在中,BC=3AB-6,点E,F分别在边AB,CD上,AE=CF,直线EF分别交AD,CB的延长线交于点H,G.
(第21题)
(1)求证:DH=BG.
(2)作HM∥AB,交BC延长线于点M,AM交GH于点O.若BE=1,GB=3,AB⊥AM,∠AEH=45°,求AE的长.
22.(本题满分12分)如图,某数学展厅的入口设计,∠ACB=90°,AC=4m,AB=5m,以△ABC的各边为边向外构造正方形ACED,正方形CBGF,正方形ABHM,在点D,G处按竖直方向悬挂霓虹灯管DN,GP,且DN=GP.
(第22题)
(1)求灯管DN,GP之间的距离.
(2)求点N,P离水平地面MH的高度差.
23.(本题满分12分)
确定有效消毒的时间段
背景素材 预防传染病,某校定期对教室进行“药熏消毒”.已知药物释放阶段,室内每立方米空气中的含药量y(mg)与释放时间x(min)成一次函数;释放后,y与x成反比例如图1所示,且2min时,室内每立方米空气中的含药量y(mg)达到最大值.某兴趣小组记录部分y(mg)与x(min)的测量数据如表1.满足的自变量x(min)的取值范围为有效消毒时间段. x…0.511.522.53…y…2.533.543.22.67…
表1
问题解决
任务1 确定y关于x的一次函数及反比例函数的表达式.
任务2 初步确定有效消毒时间段即自变量x的取值范围.
任务3 若实际生活中有效消毒时间段要求满足a≤x≤3a,其中a为常数,请确定实际生活中有效消毒的时间段.
2023学年第一学期九年级入学监测数学卷
参考答案和评分标准
一、选择题(本题有10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C B A A C D A D
二、填空题(本题有6小题,每小题4分,共24分)
11.2a-3b 12.4 13.2 14.145° 15.-4 16.;
三、解答题(本题有7小题,共66分)
17.(本题6分)
解:可以选②或③
②,,,;
③,,,.
18.(本题8分)
解:(1)全社区拥有电动汽车的数量=150÷50%=300(辆);
B小区拥有电动汽车的数量=300×25%=75(辆):补全条形统计图(略).
(2)由于A小区拥有电动汽车的数量最多,其次是B小区,建议该社区为A,B小区多购买充电桩,多安排场地安装充电桩等.
19.(本题8分)
(1)证明:在中,DC∥AB,DC=AB,
∵AE+FB=GC,∴DC-GC=AB-AE-FB,即DG=EF.
∵DC∥AB,∴DG∥EF,∴四边形DEFG为平行四边形.
∵DE⊥AB,∴为矩形.
(2)解:设AE=FB=x,则GC=2x,EF=DG=x,AD=28-3x,
在Rt△ADE中,由勾股定理,得(28-3x)2=x2+82,
化简,得x2-21x+90=0,解得x=6,或x=15(舍去)
∴种植花卉区域四边形DEFG的面积=8x=48m2.
20.(本题10分)
解(1)由,得a-c=2b-4c,3c=2b-a.
(2)把3c=2b-a代入,得
.
21.(本题10分)
(1)证明:在中,AD∥BC,∠A=∠C,AD=CB,
(第21题)
∵AD∥BC,∴∠G=∠H.
∵∠A=∠C,AE=CF,∴△AEH≌△CFG,∴AH=CG.
∵AD=CB,∴AH-AD=CG-CB,即DH=BG.
(2)解:由AB⊥AM,∠AEH=45°,得∠MOH=∠AOE=45°,由HM∥AB,得∠OHM=∠AEO=45°,设AO=AE=x,则OM=HM=AB=x+1,BC=3AB-6=3x-3,CM=DH=BG=3,BM=BC+CM=3x,在Rt△ABM中,由勾股定理,得-AB2+AM2=BM2,
即(x+1)2+(2x+1)2=(3x)2.解得,或(舍去),.
22.(本题12分)
解:(1)分别过点D,C,G作AB的垂线,垂足分别为R,S,T.
(第22题)
在正方形ACED中,AD=AC,∠DAC=90°.
由DR⊥AB,CS⊥AB,得∠CAS=∠ADR,∠CSA=∠ARD,
∴△CAS≌△ADR,∴AR=CS,DR=AS.同理GT=BS,BT=CS.
在Rt△ABC中,由勾股定理,得.
∴灯管DN,GP之间的距离.
(2)∵DN=GP,∴点N,P离水平地面MH的高度差=点D,G离水平地面MH的高度差=DR-GT=AS-BS.
在Rt△ACS中,.
∴点N,P离水平地面MH的高度差.
23.(本题12分)
任务1
解:设当药物释放阶段(即0≤x≤2)时,设y=kx+b,把,代入y=kx+b,
得,解得,∴;
设当药物释放后(即x≥2)时,设,把代入,得,解得.
任务2 把分别代入,得,解得,
由图象,得.
任务3 (1)当3a≤2时,
把代入y=x+2,得,解得;
把x=3a=2代入y=x+2,得y=4,满足题意;
.
(2)a≥2时,把代入,得,解得a=1(舍去);
∴无解.
(3)a≤2≤3a时,(即)
①把代入y=x+2,得解得;
把x=3a=2代入,解得y=4,满足要求(),∴.
②把代入,得,解得a=1;
把x=a=1代入y=x+2,解得y=3,满足要求(),∴1(min)≤x≤3(min).
综上,,或1(min)≤x≤3(min).
2023.9
卷首语:
1.本卷共4页,考试时间120分钟,满分120分;
2.全卷由试题卷和答题卡两部分组成,请将答案写在答题卡相应的位置;
3.书写时字迹要工整,清晰,请勿使用涂改液、修正带等,不得使用计算器。
希望你沉着冷静,让智慧在笔尖流淌,用细心为成功奠基!
卷Ⅰ
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选均不给分)
1.若二次根式有意义,则m的取值范围是( )
A. B. C. D.
2.在平面直角坐标系中,若点A(m,2)与点B(3,n)关于y轴对称,则m,n的值分别为( )
A.-3,-2 B.-3,2 C.3,-2 D.3,2
3.下列选项中,化简正确的是( )
A. B. C. D.
4.对温州某社区居民最爱吃的鱼类进行问卷调查后(每人选一种),绘制成如图所示统计图,已知选择带鱼的有45人,那么选择鲳鱼的有( )
(第4题)
A.15人 B.30人 C.45人 D.60人
5.在中,,则的度数是( )
A.70° B.80° C.90° D.110°
6.不等式组的解在数轴上的表示如图所示,则a的值为( )
(第6题)
A.8 B.9 C.10 D.11
7.用因式分解法解方程9x2=(x-2)2时,因式分解结果正确的是( )
A.4(2x-1)(x-1)=0 B.4(2x+1)(x-1)=0
C.4(2x-1)(x+1)=0 D.4(2x+1)(x+1)=0
8.某品牌衬衫原来每件售价400元,经过连续两次降价后,现在每件的售价为200元.设平均每次降价的百分率为x,根据题意所列方程为( )
A.200(1+2x)=400 B.400(1-2x)=200
C.200(1+x)2=400 D.400(1-x)2=200
9.对于反比例函数,当-1<y≤2,且y≠0时,自变量x的取值范围是( )
A.x≥1或x<-2 B.x≥1或x≤-2
C.0<x≤1或x<-2 D.-2<x<0或x≥1
10.在菱形ABCD中,∠B=60°,用六条线段(虚线表示)把菱形分割成四部分,如图所示,其中PM∥EF∥BC,PF∥MN∥CD,FG∥MH∥AC,且点P在对角线AC上,若求该六条割线长(虚线部分)的和,只需知道( )
(第10题)
A.六边形PMHCGF的周长 B.梯形EFGB的周长
C.梯形MNDH的周长 D.菱形ABCD的周长
二、填空题(本题有6小题,每小题4分,共24分)
11.“a的2倍与b的3倍的差”用代数式表示为_________.
12.关于x的方程x2+4x+m=0有两个相等的实数根,则m的值是_________.
13.计算:_________.
14.如图,在矩形ABCD中,点E,F均在对角线BD上,AE=ED,FG∥AE交边BC于点G.若∠AED=110°,则∠FGC的度数为_________.
(第14题)
15.对于一次函数y=ax+b(a,b为常数,且a≠0),部分的自变量x与函数y的对应值如下表:
x … -2 -1 0 1 2 …
y=ax+b … 8 5 2 -1 -4 …
若-28≤y≤14,则x的最小值为_________.
16.如图,点A,B依次在反比例函数(常数k1>0,x>0)的图象上,点C,D依次在反比例函数(常数k2<0,x>0)的图象上,AC=4BD,AC∥BD∥y轴,AE,CF分别垂直y轴于点E,F,BG⊥AC于点G,DH⊥AC于点H.若EO=2FO,阴影部分面积为8,则k1,k2的值分别为_________.
(第16题)
三、解答题(本题有7小题,共66分.解答需要写出必要的文字说明、演算步骤或证明过程)
17.(本题满分6分)设一元二次方程4x2+bx+c=0.在下面的四组条件中选择其中一组b,c的值,使这个方程有两个不相等的实数根,并解这个方程。
①b=4,c=1;②b=5,c=1;③b=-3,c=-1;④b=2,c=1.
注:如果选择多组条件分别作答,按第一个解答计分.
18.(本题满分8分)某社区为更合理配置电动汽车的充电器材及场地,需要了解本社区居民已购买电动汽车的数量,故组织全社区居民做一次问卷调查(每辆电动汽车选一小区),并制作统计图如图所示.
(第18题)
(1)求全社区及B小区拥有电动汽车的数量,并补全条形统计图.
(2)根据各小区拥有电动汽车的数量的情况,对该社区提出2条有关电动汽车的充电器材及场地配置的建议.
19.(本题满分8分)如图,地块的周长为56m,四边形DEFG为种植花卉区域,DE⊥AB于点E,DE=8m,点F,G分别在边EB,CD上,且AE+FB=GC.
(第19题)
(1)求证:四边形DEFG为矩形.
(2)若AE=FB,GC=2DG,求种植花卉区域四边形DEFG的面积.
20.(本题满分10分)已知.
(1)求c的值(用含a,b的代数式表示).
(2)若,求k的值.
21.(本题满分10分)如图,在中,BC=3AB-6,点E,F分别在边AB,CD上,AE=CF,直线EF分别交AD,CB的延长线交于点H,G.
(第21题)
(1)求证:DH=BG.
(2)作HM∥AB,交BC延长线于点M,AM交GH于点O.若BE=1,GB=3,AB⊥AM,∠AEH=45°,求AE的长.
22.(本题满分12分)如图,某数学展厅的入口设计,∠ACB=90°,AC=4m,AB=5m,以△ABC的各边为边向外构造正方形ACED,正方形CBGF,正方形ABHM,在点D,G处按竖直方向悬挂霓虹灯管DN,GP,且DN=GP.
(第22题)
(1)求灯管DN,GP之间的距离.
(2)求点N,P离水平地面MH的高度差.
23.(本题满分12分)
确定有效消毒的时间段
背景素材 预防传染病,某校定期对教室进行“药熏消毒”.已知药物释放阶段,室内每立方米空气中的含药量y(mg)与释放时间x(min)成一次函数;释放后,y与x成反比例如图1所示,且2min时,室内每立方米空气中的含药量y(mg)达到最大值.某兴趣小组记录部分y(mg)与x(min)的测量数据如表1.满足的自变量x(min)的取值范围为有效消毒时间段. x…0.511.522.53…y…2.533.543.22.67…
表1
问题解决
任务1 确定y关于x的一次函数及反比例函数的表达式.
任务2 初步确定有效消毒时间段即自变量x的取值范围.
任务3 若实际生活中有效消毒时间段要求满足a≤x≤3a,其中a为常数,请确定实际生活中有效消毒的时间段.
2023学年第一学期九年级入学监测数学卷
参考答案和评分标准
一、选择题(本题有10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C B A A C D A D
二、填空题(本题有6小题,每小题4分,共24分)
11.2a-3b 12.4 13.2 14.145° 15.-4 16.;
三、解答题(本题有7小题,共66分)
17.(本题6分)
解:可以选②或③
②,,,;
③,,,.
18.(本题8分)
解:(1)全社区拥有电动汽车的数量=150÷50%=300(辆);
B小区拥有电动汽车的数量=300×25%=75(辆):补全条形统计图(略).
(2)由于A小区拥有电动汽车的数量最多,其次是B小区,建议该社区为A,B小区多购买充电桩,多安排场地安装充电桩等.
19.(本题8分)
(1)证明:在中,DC∥AB,DC=AB,
∵AE+FB=GC,∴DC-GC=AB-AE-FB,即DG=EF.
∵DC∥AB,∴DG∥EF,∴四边形DEFG为平行四边形.
∵DE⊥AB,∴为矩形.
(2)解:设AE=FB=x,则GC=2x,EF=DG=x,AD=28-3x,
在Rt△ADE中,由勾股定理,得(28-3x)2=x2+82,
化简,得x2-21x+90=0,解得x=6,或x=15(舍去)
∴种植花卉区域四边形DEFG的面积=8x=48m2.
20.(本题10分)
解(1)由,得a-c=2b-4c,3c=2b-a.
(2)把3c=2b-a代入,得
.
21.(本题10分)
(1)证明:在中,AD∥BC,∠A=∠C,AD=CB,
(第21题)
∵AD∥BC,∴∠G=∠H.
∵∠A=∠C,AE=CF,∴△AEH≌△CFG,∴AH=CG.
∵AD=CB,∴AH-AD=CG-CB,即DH=BG.
(2)解:由AB⊥AM,∠AEH=45°,得∠MOH=∠AOE=45°,由HM∥AB,得∠OHM=∠AEO=45°,设AO=AE=x,则OM=HM=AB=x+1,BC=3AB-6=3x-3,CM=DH=BG=3,BM=BC+CM=3x,在Rt△ABM中,由勾股定理,得-AB2+AM2=BM2,
即(x+1)2+(2x+1)2=(3x)2.解得,或(舍去),.
22.(本题12分)
解:(1)分别过点D,C,G作AB的垂线,垂足分别为R,S,T.
(第22题)
在正方形ACED中,AD=AC,∠DAC=90°.
由DR⊥AB,CS⊥AB,得∠CAS=∠ADR,∠CSA=∠ARD,
∴△CAS≌△ADR,∴AR=CS,DR=AS.同理GT=BS,BT=CS.
在Rt△ABC中,由勾股定理,得.
∴灯管DN,GP之间的距离.
(2)∵DN=GP,∴点N,P离水平地面MH的高度差=点D,G离水平地面MH的高度差=DR-GT=AS-BS.
在Rt△ACS中,.
∴点N,P离水平地面MH的高度差.
23.(本题12分)
任务1
解:设当药物释放阶段(即0≤x≤2)时,设y=kx+b,把,代入y=kx+b,
得,解得,∴;
设当药物释放后(即x≥2)时,设,把代入,得,解得.
任务2 把分别代入,得,解得,
由图象,得.
任务3 (1)当3a≤2时,
把代入y=x+2,得,解得;
把x=3a=2代入y=x+2,得y=4,满足题意;
.
(2)a≥2时,把代入,得,解得a=1(舍去);
∴无解.
(3)a≤2≤3a时,(即)
①把代入y=x+2,得解得;
把x=3a=2代入,解得y=4,满足要求(),∴.
②把代入,得,解得a=1;
把x=a=1代入y=x+2,解得y=3,满足要求(),∴1(min)≤x≤3(min).
综上,,或1(min)≤x≤3(min).
同课章节目录
