同底数幂的乘法(安徽省芜湖市芜湖县)
文档属性
| 名称 | 同底数幂的乘法(安徽省芜湖市芜湖县) |

|
|
| 格式 | rar | ||
| 文件大小 | 816.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-21 00:00:00 | ||
图片预览





文档简介
课件12张PPT。2007-2008年度第一学期
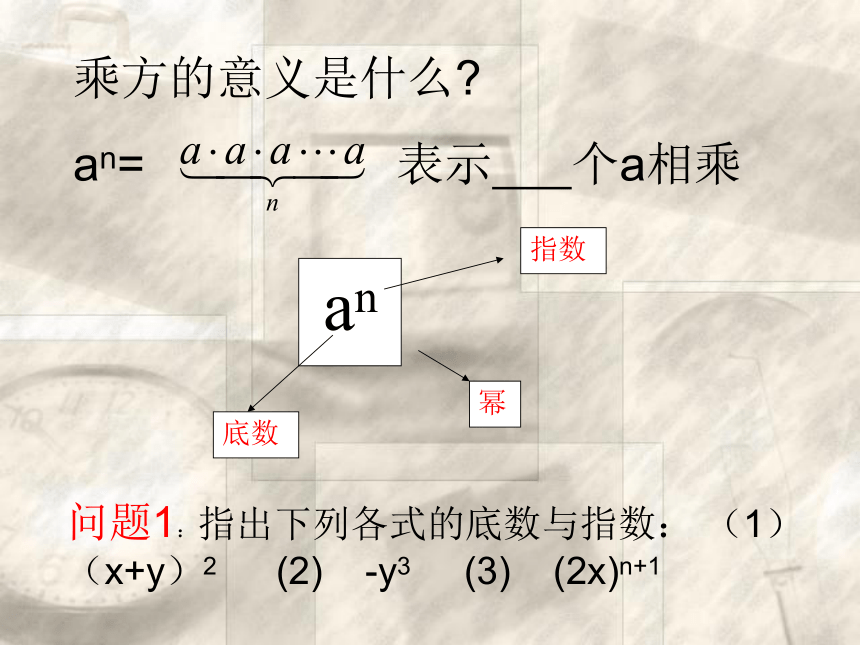
陶辛片教研活动数学公开课15.2.1 同底数幂的乘法乘方的意义是什么?
an= 表示 个a相乘问题1:指出下列各式的底数与指数: (1)(x+y)2 (2) -y3 (3) (2x)n+1我们来看下面的问题2吧一种电子计算机每秒可进行1012次运算,它工作103秒可进行多少次运算?根据乘方的意义可知:
1012×103=(10×…×10) ×(10×10×10)
=(10×10×…×10)
=101512个1015个10分析: 运算次数=运算速度×工作时间通过观察大家可以发现1012、103这两个因数是同底数幂的形式,所以我们把像1012×103的运算叫做同底数幂的乘法. 探究
根据乘方的意义填空,看看计算结果有什么规律:
(1) 25×22=2( ) ;
a5?a2=a ( ) ; (3) 5m?5n = 5 ( ) .一般地,我们有am·an=am+n(m,n都是正整数)(反过来仍然成立)即同底数幂相乘,底数不变,指数相加.对于任意底数a与任意正整数m,n,am·an==am+n=例1 计算:
(1) x2·x5; (2) a·a6; (3) 2×24×23; (4) xm·x3m+1.解: (1)x2·x5 =x2+5 =x 7. (4) xm·x3m+1=xm+3m+1 = x 4m+1.(3)2×24×23=21+4+3=28.(2) a·a6 =a1+6 =a7.动动脑
不要像我一样懒哟! [例2]计算am·an·ap(m、n、p为正整数)。 提出问题3:由例1的第三小题和例2我们会得到什么样的启示呢?
提出问题4:能不能用符号表示出来呢?
符号表示为:
am1am2am3???amn= a(m1+m2+m3+???+mn) =(am·an)ap=am+nap =am+n+p
或=(amap)an=am+pan =am+p+n
或=am(anap)=aman+p =am+n+p
练习
计算:
b5·b ; (2) 10×102×103;
(3) –a2·a6; (4) y2n·yn+1.仔细做一做
计算:
1 .-x2·(-x)5 · (-x); 2.(x+y)m-1·(x+y)m+1·(x+y)3-m;
3. (x-y)3(y-x)2.思维延伸
1已知xa=2,xb=3,求xa+b.
2已知x3·xa·x2a+1=x31,求a的值.1.已知:xa=2,xb=3,求xa+b
解:am·an=am+n反过来,其逆向运算am+n=am·an
∴xa+b=xa·xb=2×3=62.已知:x3·xa·x2a+1=x31,求a
解:∵x3·xa·x2a+1=x3+a+(2a+1)=x3a+4
∴x3a+4=x31(底数相同,幂相等则指数肯定相等) ∴ 3a+4=31 a=9
这节课我们学习了同底数幂的乘法的运算性质,请同学们谈一下有何新收 获和体会呢?进一步体会了幂的意义.了解了同底数幂乘法的运算性质.
必须是同底数幂的乘法才能运用这个性质
一定是底数不变,指数相加而不是相乘(这一点我们的同学最易犯得错误)课后作业
1.课本P177习题15.2─1.(1)、(2); 2.(1);8.
补充: 已知2x=3,2y=6,2z=36,试写出x,y,z的关系式再见3 .(x-y)3·(y-x)2
解法一: 解法二:
=(x-y)3·(x-y)2 =〔-(y-x)〕3·(x-y)2
=(x-y)3+2 =-(y-x)3·(y-x)2
=(x-y)5 =-(y-x)3+2
=-(y-x)5
=-〔-(x-y)5=(x-y)51. -x2·(-x)5·(-x) 解法一: 二:解法二: =-(-x)2·(-x)5·(-x) =-x2·(-x5) ·(-x) =-(-x)2+5+1 =-x2·x5·x =-(-x)8 =-x2+5+1 =-x8 =-x8
an= 表示 个a相乘问题1:指出下列各式的底数与指数: (1)(x+y)2 (2) -y3 (3) (2x)n+1我们来看下面的问题2吧一种电子计算机每秒可进行1012次运算,它工作103秒可进行多少次运算?根据乘方的意义可知:
1012×103=(10×…×10) ×(10×10×10)
=(10×10×…×10)
=101512个1015个10分析: 运算次数=运算速度×工作时间通过观察大家可以发现1012、103这两个因数是同底数幂的形式,所以我们把像1012×103的运算叫做同底数幂的乘法. 探究
根据乘方的意义填空,看看计算结果有什么规律:
(1) 25×22=2( ) ;
a5?a2=a ( ) ; (3) 5m?5n = 5 ( ) .一般地,我们有am·an=am+n(m,n都是正整数)(反过来仍然成立)即同底数幂相乘,底数不变,指数相加.对于任意底数a与任意正整数m,n,am·an==am+n=例1 计算:
(1) x2·x5; (2) a·a6; (3) 2×24×23; (4) xm·x3m+1.解: (1)x2·x5 =x2+5 =x 7. (4) xm·x3m+1=xm+3m+1 = x 4m+1.(3)2×24×23=21+4+3=28.(2) a·a6 =a1+6 =a7.动动脑
不要像我一样懒哟! [例2]计算am·an·ap(m、n、p为正整数)。 提出问题3:由例1的第三小题和例2我们会得到什么样的启示呢?
提出问题4:能不能用符号表示出来呢?
符号表示为:
am1am2am3???amn= a(m1+m2+m3+???+mn) =(am·an)ap=am+nap =am+n+p
或=(amap)an=am+pan =am+p+n
或=am(anap)=aman+p =am+n+p
练习
计算:
b5·b ; (2) 10×102×103;
(3) –a2·a6; (4) y2n·yn+1.仔细做一做
计算:
1 .-x2·(-x)5 · (-x); 2.(x+y)m-1·(x+y)m+1·(x+y)3-m;
3. (x-y)3(y-x)2.思维延伸
1已知xa=2,xb=3,求xa+b.
2已知x3·xa·x2a+1=x31,求a的值.1.已知:xa=2,xb=3,求xa+b
解:am·an=am+n反过来,其逆向运算am+n=am·an
∴xa+b=xa·xb=2×3=62.已知:x3·xa·x2a+1=x31,求a
解:∵x3·xa·x2a+1=x3+a+(2a+1)=x3a+4
∴x3a+4=x31(底数相同,幂相等则指数肯定相等) ∴ 3a+4=31 a=9
这节课我们学习了同底数幂的乘法的运算性质,请同学们谈一下有何新收 获和体会呢?进一步体会了幂的意义.了解了同底数幂乘法的运算性质.
必须是同底数幂的乘法才能运用这个性质
一定是底数不变,指数相加而不是相乘(这一点我们的同学最易犯得错误)课后作业
1.课本P177习题15.2─1.(1)、(2); 2.(1);8.
补充: 已知2x=3,2y=6,2z=36,试写出x,y,z的关系式再见3 .(x-y)3·(y-x)2
解法一: 解法二:
=(x-y)3·(x-y)2 =〔-(y-x)〕3·(x-y)2
=(x-y)3+2 =-(y-x)3·(y-x)2
=(x-y)5 =-(y-x)3+2
=-(y-x)5
=-〔-(x-y)5=(x-y)51. -x2·(-x)5·(-x) 解法一: 二:解法二: =-(-x)2·(-x)5·(-x) =-x2·(-x5) ·(-x) =-(-x)2+5+1 =-x2·x5·x =-(-x)8 =-x2+5+1 =-x8 =-x8
