1.3 探索三角形全等的条件(5) 课件(15张PPT)
文档属性
| 名称 | 1.3 探索三角形全等的条件(5) 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 08:25:32 | ||
图片预览




文档简介
(共15张PPT)
数学
八年级上册
苏科版 八年级上册
1.3 探索三角形全等的条件(5)
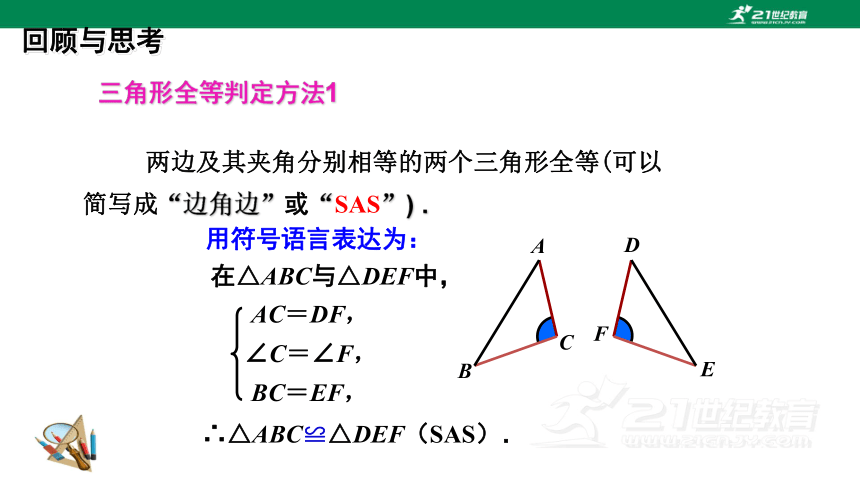
三角形全等判定方法1
用符号语言表达为:
在△ABC与△DEF中,
∴△ABC≌△DEF(SAS).
两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”) .
F
E
D
C
B
A
AC=DF,
∠C=∠F,
BC=EF,
回顾与思考
两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
F
E
D
C
B
A
三角形全等判定方法2
在△ABC与△DEF中,
∴△ABC≌△DEF(ASA).
∠A=∠D,
AB=DE,
∠B=∠E,
用符号语言表达为:
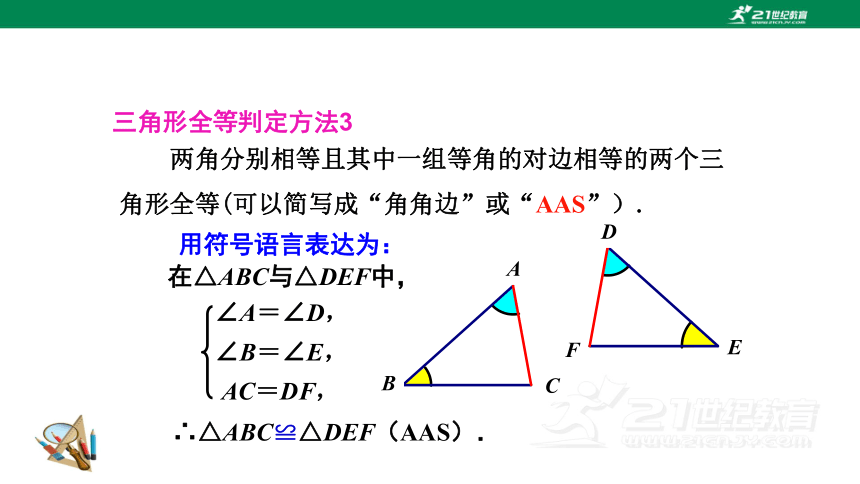
三角形全等判定方法3
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
用符号语言表达为:
在△ABC与△DEF中,
∴△ABC≌△DEF(AAS).
∠A=∠D,
∠B=∠E,
AC=DF,
A
C
B
F
D
E
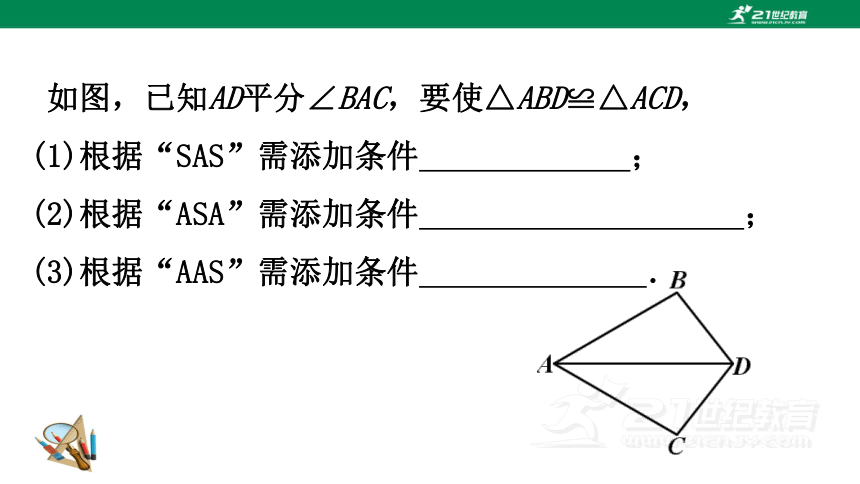
如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件 ;
(2)根据“ASA”需添加条件 ;
(3)根据“AAS”需添加条件 .
1.如图,∠A=∠B,∠1=∠2,EA=EB,你能证明AC=BD吗
分析与讨论
2.如图,点C、F在AD上,且AF=DC,∠B=∠E,
∠A=∠D, 你能证明AB=DE吗
1.为了利用“ASA”或 “AAS”定理判定两个三角形全等,有时需要先把已知中的某个条件,转变为判定三角形全等的直接条件.
归纳与总结
2.证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到.
注意分清题中直接给出的条件、间接给出的条件以及图中隐含的条件
理解与应用
例6 已知:如图,点A、B、C、D在一条直线上,EA∥FB,EC∥FD,EA=FB.求证:AB=CD.
上面的推理过程可以用符号“ ”简明地表述如下:
理解与应用
EA∥FB ∠A=∠FBD
EC∥FD ∠ECA=∠D △EAC≌△FBD △EAC≌△FBD
EA=FB
AC=BD AB+BC=CD+BC AB=CD
课堂练习
1.已知:如图,AB=AC,点D、E分别在AB、AC上,∠B=∠C.求证:DB=EC .
2.已知,如图,∠ABC=∠DCB, ∠1=∠2.
求证:AB=DC.
课堂小结
通过这节课的学习与探索,你有哪些收获?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
数学
八年级上册
苏科版 八年级上册
1.3 探索三角形全等的条件(5)
三角形全等判定方法1
用符号语言表达为:
在△ABC与△DEF中,
∴△ABC≌△DEF(SAS).
两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”) .
F
E
D
C
B
A
AC=DF,
∠C=∠F,
BC=EF,
回顾与思考
两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
F
E
D
C
B
A
三角形全等判定方法2
在△ABC与△DEF中,
∴△ABC≌△DEF(ASA).
∠A=∠D,
AB=DE,
∠B=∠E,
用符号语言表达为:
三角形全等判定方法3
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
用符号语言表达为:
在△ABC与△DEF中,
∴△ABC≌△DEF(AAS).
∠A=∠D,
∠B=∠E,
AC=DF,
A
C
B
F
D
E
如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件 ;
(2)根据“ASA”需添加条件 ;
(3)根据“AAS”需添加条件 .
1.如图,∠A=∠B,∠1=∠2,EA=EB,你能证明AC=BD吗
分析与讨论
2.如图,点C、F在AD上,且AF=DC,∠B=∠E,
∠A=∠D, 你能证明AB=DE吗
1.为了利用“ASA”或 “AAS”定理判定两个三角形全等,有时需要先把已知中的某个条件,转变为判定三角形全等的直接条件.
归纳与总结
2.证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到.
注意分清题中直接给出的条件、间接给出的条件以及图中隐含的条件
理解与应用
例6 已知:如图,点A、B、C、D在一条直线上,EA∥FB,EC∥FD,EA=FB.求证:AB=CD.
上面的推理过程可以用符号“ ”简明地表述如下:
理解与应用
EA∥FB ∠A=∠FBD
EC∥FD ∠ECA=∠D △EAC≌△FBD △EAC≌△FBD
EA=FB
AC=BD AB+BC=CD+BC AB=CD
课堂练习
1.已知:如图,AB=AC,点D、E分别在AB、AC上,∠B=∠C.求证:DB=EC .
2.已知,如图,∠ABC=∠DCB, ∠1=∠2.
求证:AB=DC.
课堂小结
通过这节课的学习与探索,你有哪些收获?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
