3.3勾股定理的简单应用 课件(16张PPT)
文档属性
| 名称 | 3.3勾股定理的简单应用 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
数学
七年级上册
苏科版 八年级上册
3.3勾股定理的简单应用
5
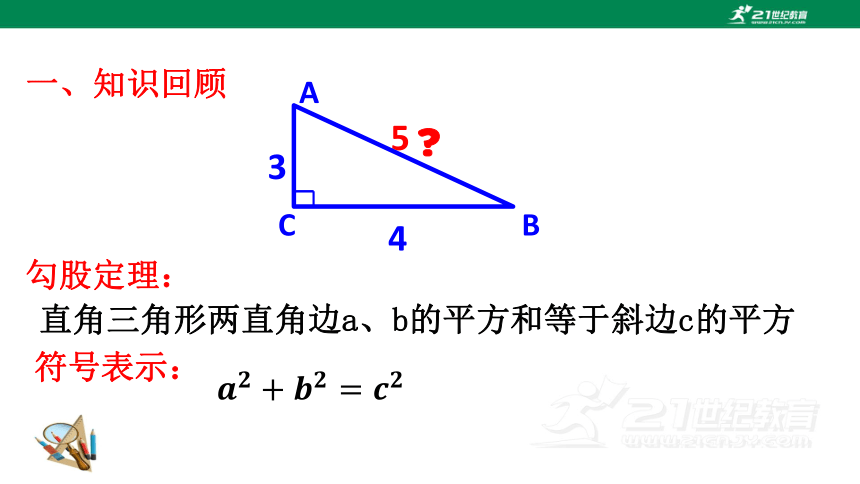
勾股定理:
直角三角形两直角边a、b的平方和等于斜边c的平方
符号表示:
一、知识回顾
B
C
3
4
A
C
A
B
3
4
5
勾股定理的逆定理:
如果三角形较小的两边a、b的平方和等于第三边c的平方,那么这个三角形是直角三角形
符号表示:
∴△ABC是直角三角形且
思考:勾股定理和逆定理有什么区别?
△ABC是什么三角形?
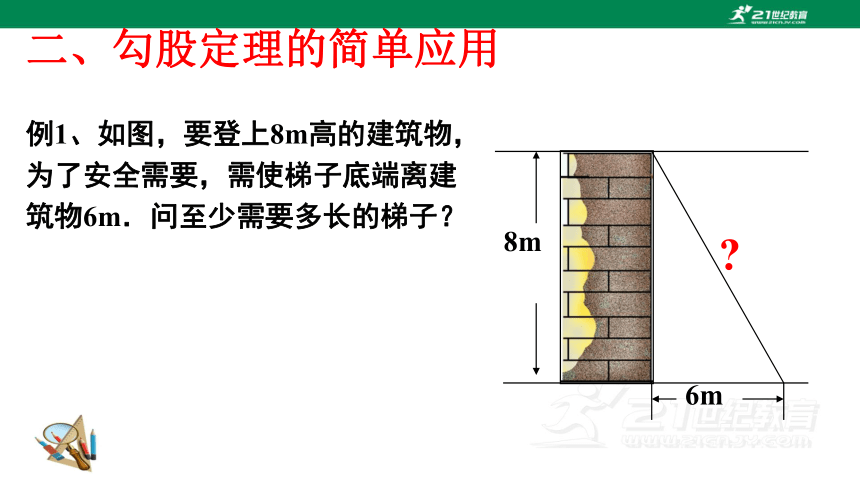
例1、如图,要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m.问至少需要多长的梯子?
8m
6m
二、勾股定理的简单应用
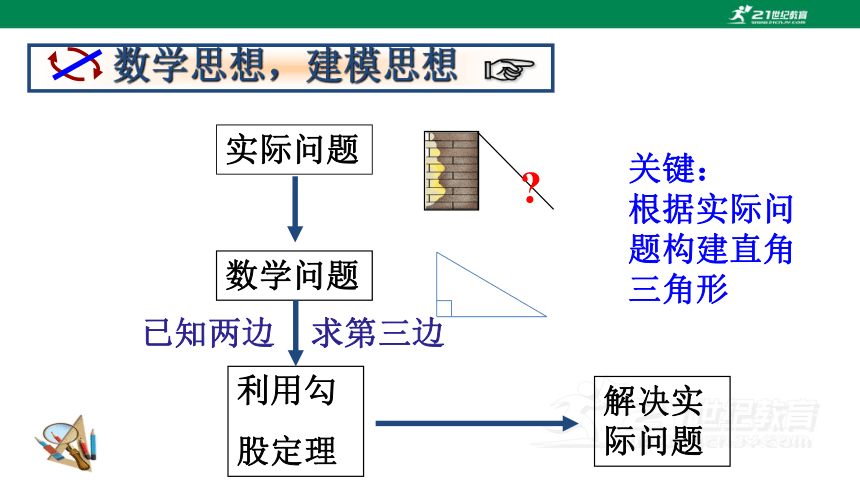
实际问题
数学问题
利用勾
股定理
已知两边
求第三边
解决实际问题
数学思想,建模思想
关键:
根据实际问题构建直角三角形
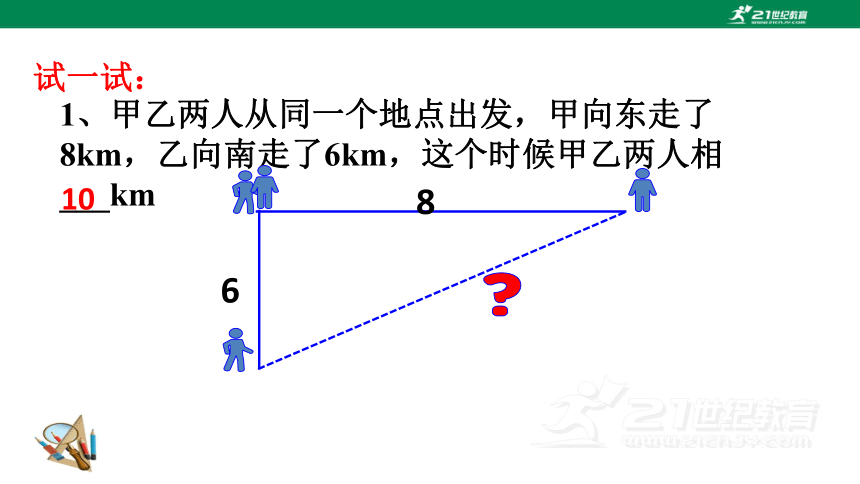
1、甲乙两人从同一个地点出发,甲向东走了8km,乙向南走了6km,这个时候甲乙两人相___km
8
6
试一试:
10
2、如图,为修铁路需凿通隧道AC,测得∠A=50°,∠B=40°,AB=5km, BC=4 km,若每天凿隧道0.3 km,问需要多少天才能把隧道凿通?
例2 九章算术中的“折竹”问题:
今有竹高一丈,末折抵地,去根三尺,问折者高几何
意思是:有一根竹子原高1丈(1丈=10尺),
中部有一处折断,竹梢触地面处离竹根3尺,
试问折断处离地面多高
A
O
B
x
(10-x)
3
A
C
B
3
1、在中, ,BC=3, 的周长为12,则AC=______
注意:在直角三角形中,当我们已知一边时,另外两边的关系除了和,也可以是差、倍数、比例等
2、在中, ,BC=3,AB-AC=1,
则AC =______
3、在中, ,BC=3,AC:AB=4:5,
则AC=_____
4
4
4
变式:
例3:如图,AD是△ ABC的中线,AD=24,AB=26,BC=20. (1)AC的长度
(2)求
(3)求△ABC中AC边上的高
S△ABC
D
C
B
A
24
26
20
?
三、利用勾股定理和逆定理解斜三角形
变式:
在△ABC中,AB=15, AC=13,AD⊥BC
交直线BC于点D,AD=12,你能求出线段BC的长度吗?
15
13
15
13
12
12
阅读课本P88《勾股定理的证明》
四、拓展延伸
两个重要定理(勾股定理及其逆定理);
两种重要思想(数形结合思想、方程思想).
勾股定理
直角三角形边
长的数量关系
勾股定理
的逆定理
直角三角
形的判定
互逆定理
五、小结思考
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
数学
七年级上册
苏科版 八年级上册
3.3勾股定理的简单应用
5
勾股定理:
直角三角形两直角边a、b的平方和等于斜边c的平方
符号表示:
一、知识回顾
B
C
3
4
A
C
A
B
3
4
5
勾股定理的逆定理:
如果三角形较小的两边a、b的平方和等于第三边c的平方,那么这个三角形是直角三角形
符号表示:
∴△ABC是直角三角形且
思考:勾股定理和逆定理有什么区别?
△ABC是什么三角形?
例1、如图,要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m.问至少需要多长的梯子?
8m
6m
二、勾股定理的简单应用
实际问题
数学问题
利用勾
股定理
已知两边
求第三边
解决实际问题
数学思想,建模思想
关键:
根据实际问题构建直角三角形
1、甲乙两人从同一个地点出发,甲向东走了8km,乙向南走了6km,这个时候甲乙两人相___km
8
6
试一试:
10
2、如图,为修铁路需凿通隧道AC,测得∠A=50°,∠B=40°,AB=5km, BC=4 km,若每天凿隧道0.3 km,问需要多少天才能把隧道凿通?
例2 九章算术中的“折竹”问题:
今有竹高一丈,末折抵地,去根三尺,问折者高几何
意思是:有一根竹子原高1丈(1丈=10尺),
中部有一处折断,竹梢触地面处离竹根3尺,
试问折断处离地面多高
A
O
B
x
(10-x)
3
A
C
B
3
1、在中, ,BC=3, 的周长为12,则AC=______
注意:在直角三角形中,当我们已知一边时,另外两边的关系除了和,也可以是差、倍数、比例等
2、在中, ,BC=3,AB-AC=1,
则AC =______
3、在中, ,BC=3,AC:AB=4:5,
则AC=_____
4
4
4
变式:
例3:如图,AD是△ ABC的中线,AD=24,AB=26,BC=20. (1)AC的长度
(2)求
(3)求△ABC中AC边上的高
S△ABC
D
C
B
A
24
26
20
?
三、利用勾股定理和逆定理解斜三角形
变式:
在△ABC中,AB=15, AC=13,AD⊥BC
交直线BC于点D,AD=12,你能求出线段BC的长度吗?
15
13
15
13
12
12
阅读课本P88《勾股定理的证明》
四、拓展延伸
两个重要定理(勾股定理及其逆定理);
两种重要思想(数形结合思想、方程思想).
勾股定理
直角三角形边
长的数量关系
勾股定理
的逆定理
直角三角
形的判定
互逆定理
五、小结思考
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
